
- •Раздел 2. Элементы векторной алгебры
- •1. Определение вектора
- •2. Направление вектора. Коллинеарность векторов
- •Свойства коллинеарных векторов:
- •3. Абсолютная величина вектора
- •4. Равенство векторов
- •5. Линейные операции над векторами
- •5.1. Сложение векторов
- •Свойства сложения:
- •5.2. Вычитание векторов
- •5.3. Умножение вектора на действительное число
- •Свойства произведения вектора на число
- •6. Векторное пространство
- •7. Линейная зависимость векторов
- •Свойства линейно зависимых векторов:
- •8. Базис системы векторов и пространства
- •Свойства базиса системы векторов:
- •9. Координаты вектора в базисе
- •Свойства координат векторов:
- •Практикум 13. Векторы. Основные понятия. Линейные операции
- •2) Выполнить оставшиеся номера
5.2. Вычитание векторов
Разность векторов существует и определена однозначно. Вычитание вводится как операция, обратная сложению.
Определение 12.
Разностью
векторов
![]() и
и
![]() ,
отложенных от общего начала, называется
вектор
,
отложенных от общего начала, называется
вектор
![]() ,
начало которого совпадает с концом
вычитаемого вектора, а конец – с концом
уменьшаемого вектора.
,
начало которого совпадает с концом
вычитаемого вектора, а конец – с концом
уменьшаемого вектора.
![]() ,
если
,
если
![]() .
.
![]() . (7.2)
. (7.2)
Для любых двух
векторов
![]() и
и
![]() :
:
![]() –
–![]() =
=![]() +(–
+(–![]() ).
).
Определение 12*.
Разностью
двух векторов
![]() и
и
![]() ,
называют третий вектор, равный сумме
уменьшаемого вектора
,
называют третий вектор, равный сумме
уменьшаемого вектора
![]() и вектора (–
и вектора (–![]() ),
противоположного вычитаемому.
),
противоположного вычитаемому.
Это определение указывает правило построения разности векторов.

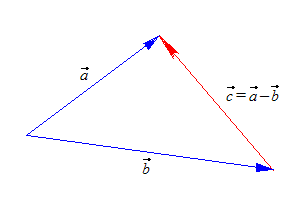
5.3. Умножение вектора на действительное число
Произведение вектора на число существует и определено однозначно.
Определение 13.
Произведением
ненулевого вектора
![]() на действительное число
на действительное число
![]() 0
называется вектор
0
называется вектор
![]() ,
удовлетворяющий следующим условиям
(7.3):
,
удовлетворяющий следующим условиям
(7.3):
-
Условие 1
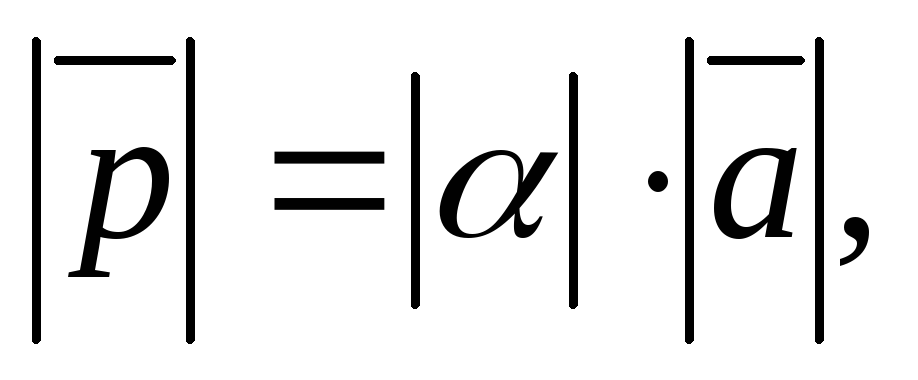 где
где
 – модуль числа
– модуль числа
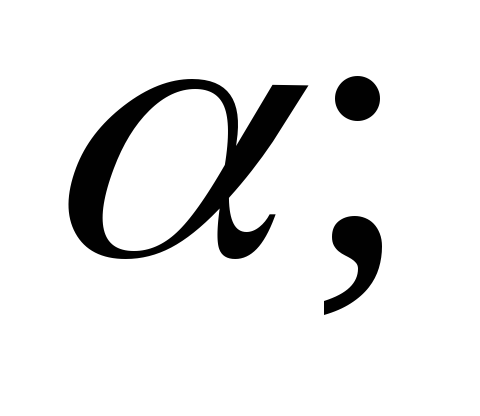
Условие 2
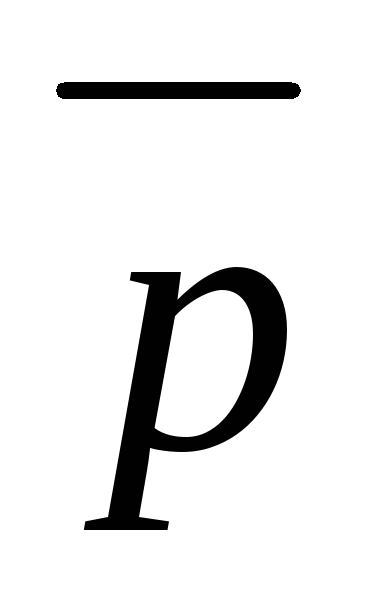

 ,
если
,
если
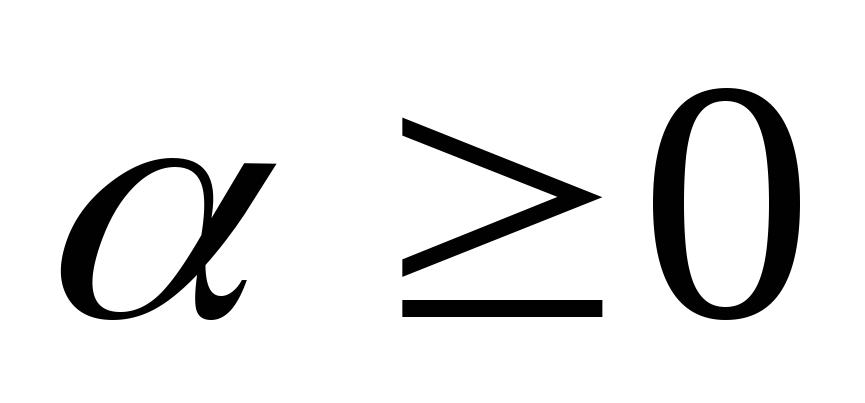 ,
,
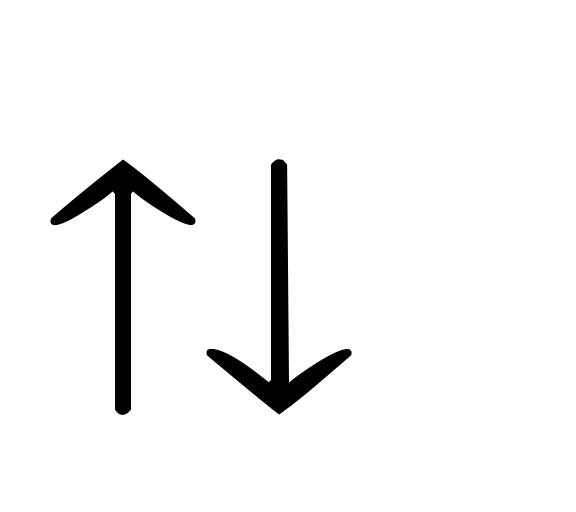
 ,
если
,
если
 <
0.
<
0.
Обозначение:
![]() =
=![]()
Пример 3.
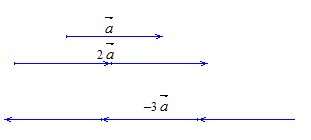
Свойства произведения вектора на число
Из определения следует:
1)
![]() ||
||
![]() ,
,
2) если
![]() =
=![]() ,
то
,
то
![]() =
=![]() =
=![]() ;
;
3) если =0,
то
![]() =0
=0![]() =
=![]() .
.
Для произвольных
чисел ,
и векторов
![]() и
и
![]() справедливы следующие равенства:
справедливы следующие равенства:
4) 1![]() =
=![]() ; 6)
; 6)
![]()
5)
![]() 7)
7)
![]()
Для доказательства достаточно рассмотреть выполнение условий определения.
Для примера докажем свойства 4-5.
4) 1![]() =
=![]()
-
Условия определения
1. Длина
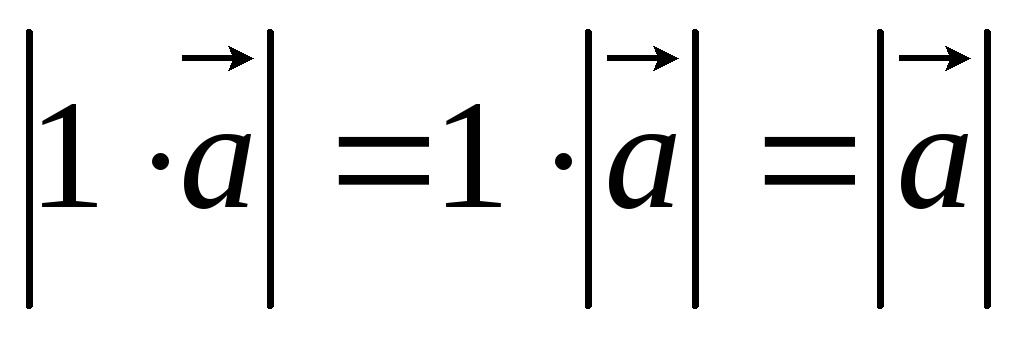
2. Направление
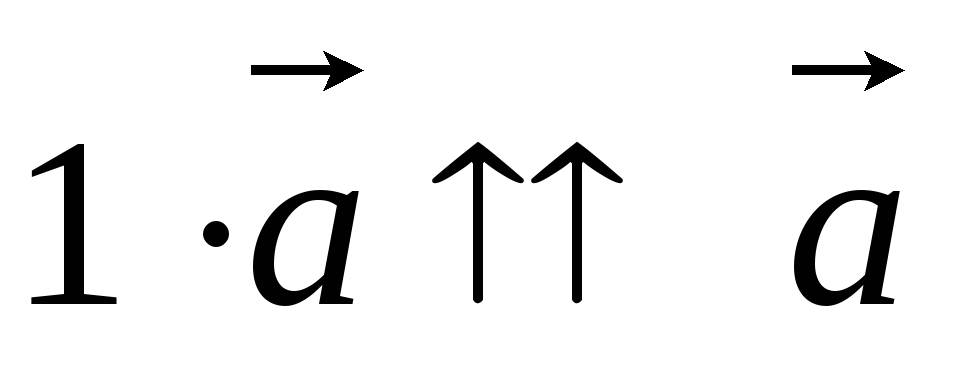 ,
так как 10.
,
так как 10.Вывод
1
 =
= .
.
5) ![]()
-
Условия
определения
Слева
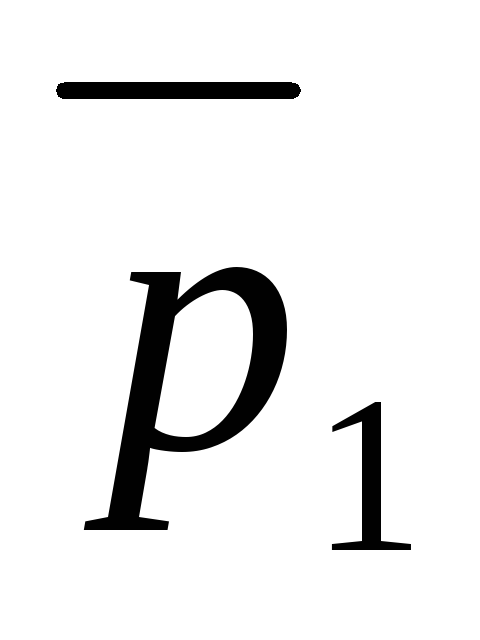
Справа

Вывод
1. Длина
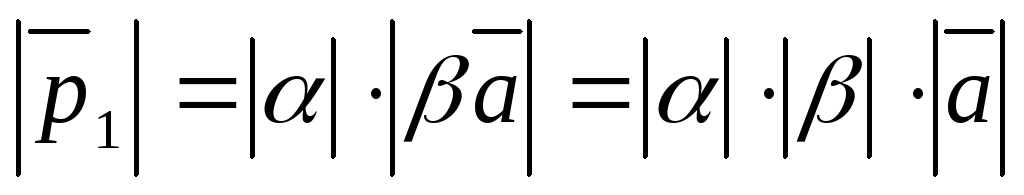
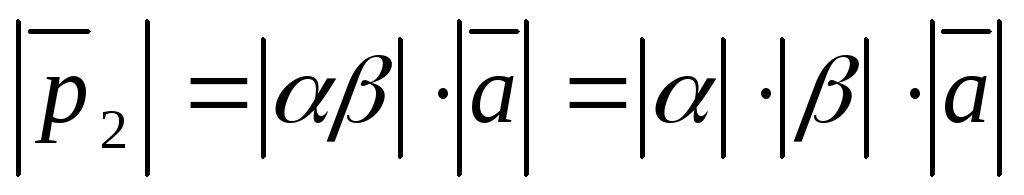
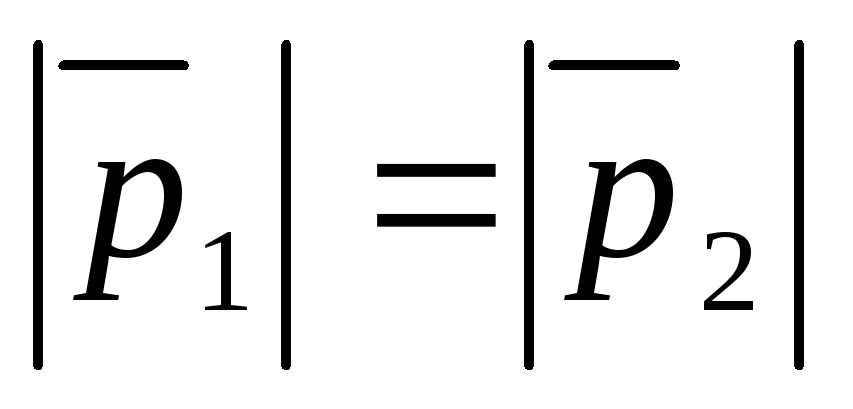
2. Направление
2.1) Если
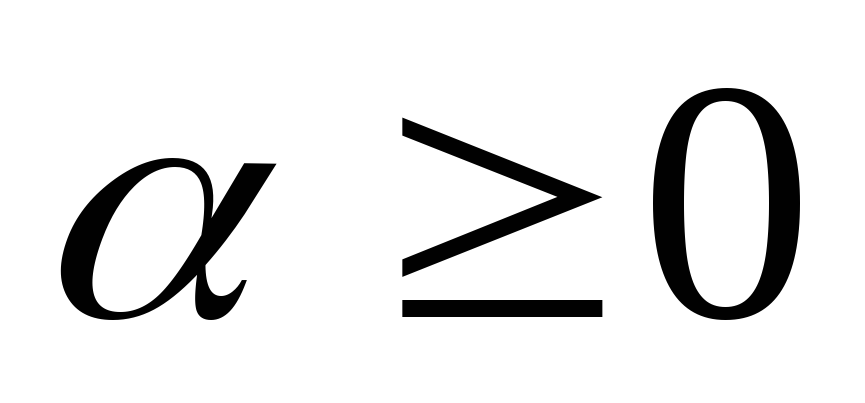 и
и
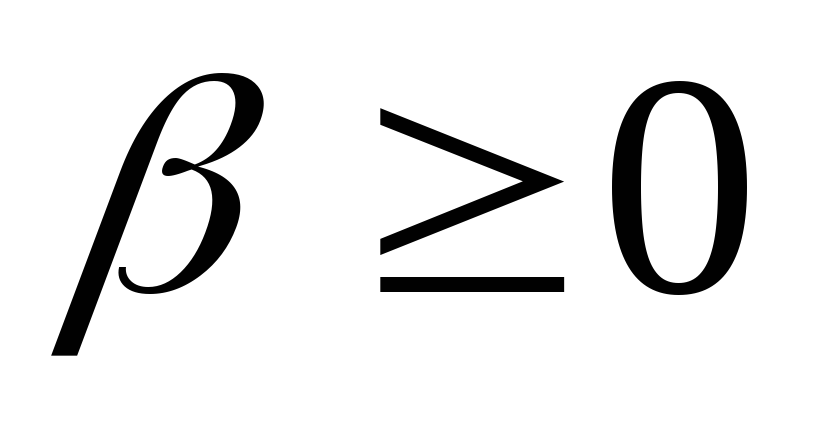 ,
,то


 и
и
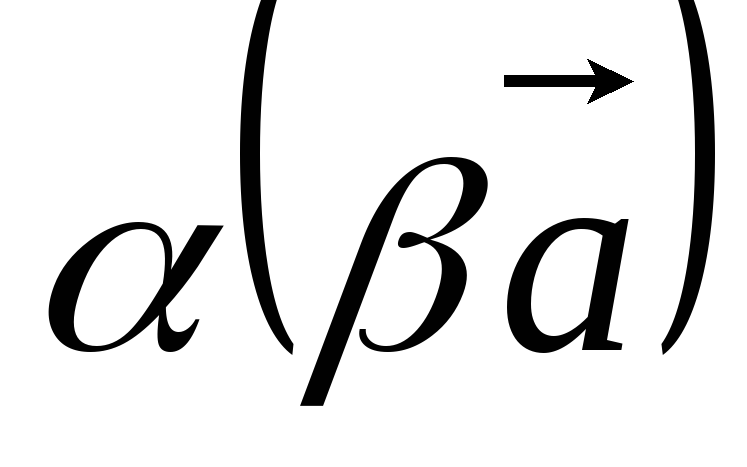

 ,
,
т.е.


 .
.то
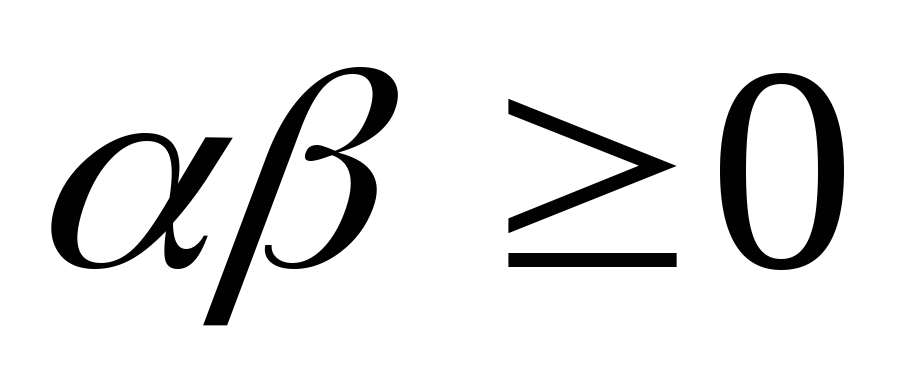 и
и
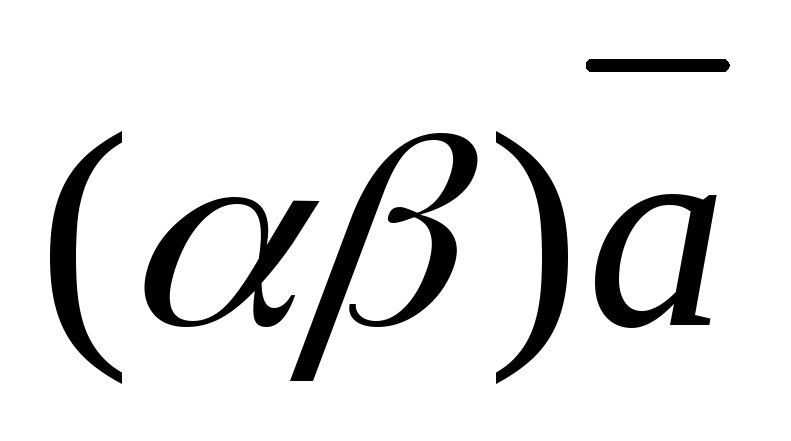

 ,
,т.е.


 .
.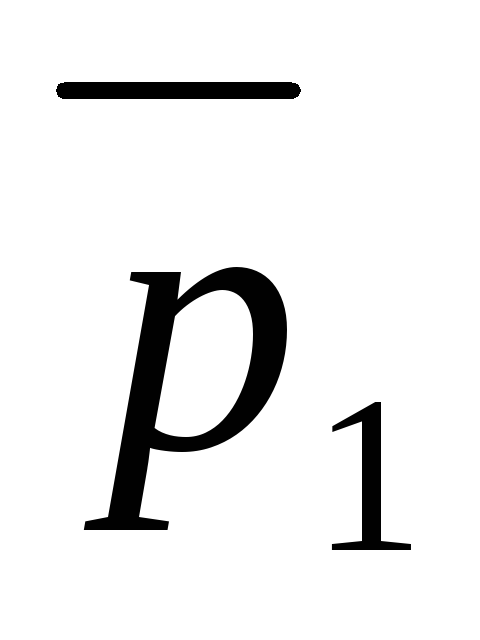

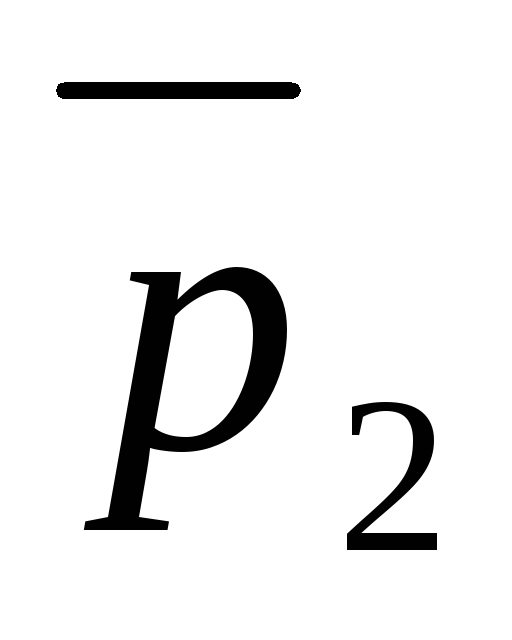
2.2) Если
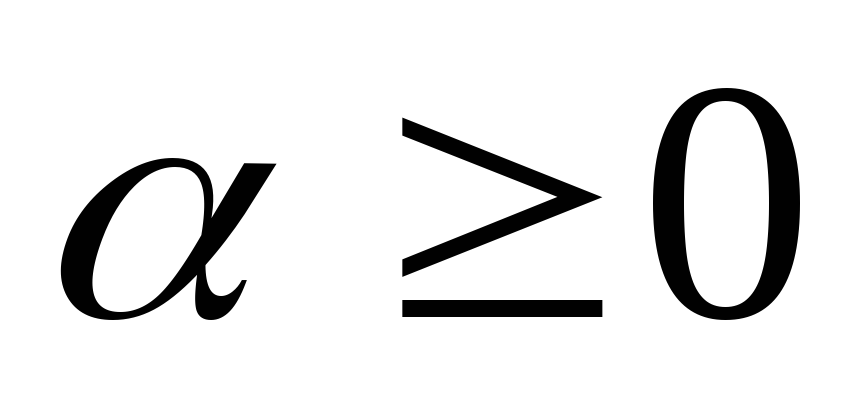 и
и
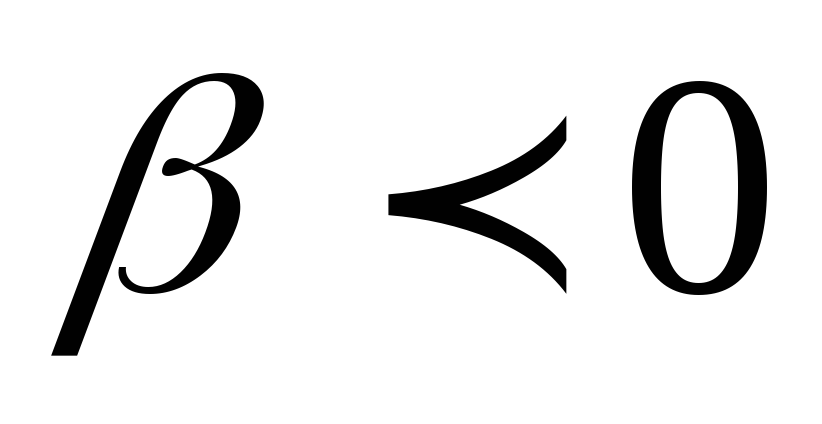 ,
,то
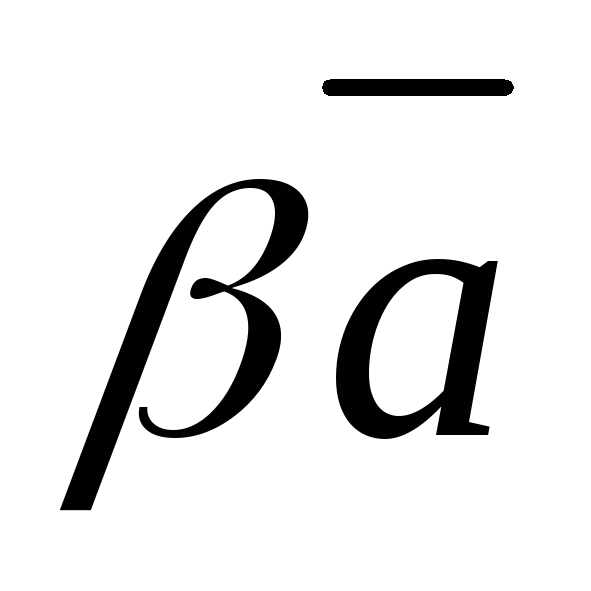
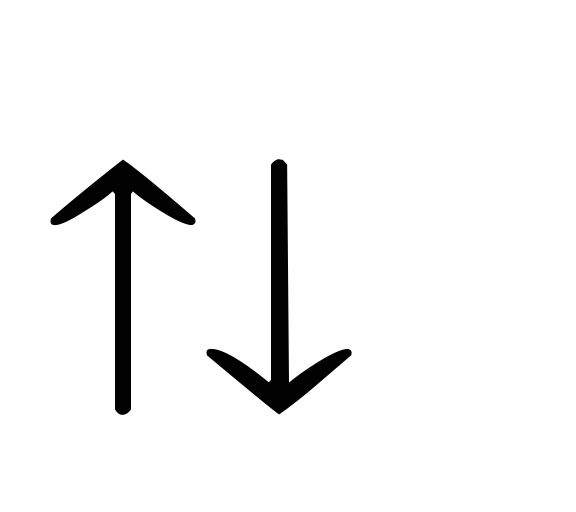
 и
и
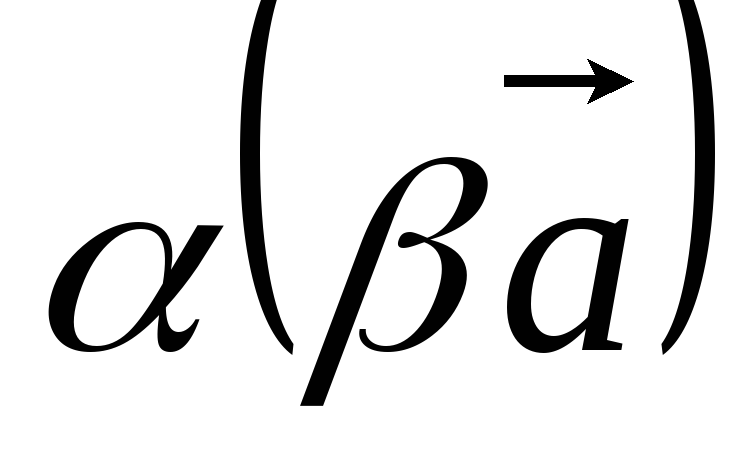
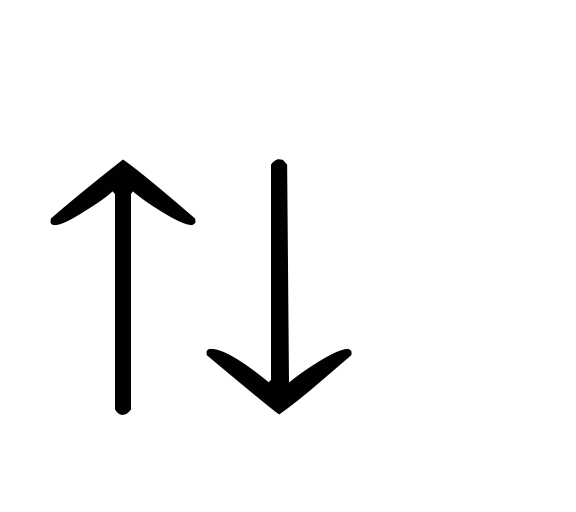
 ,
,
т.е.
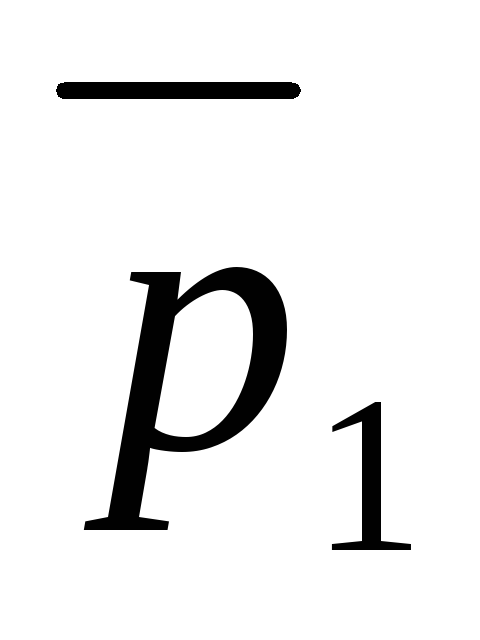
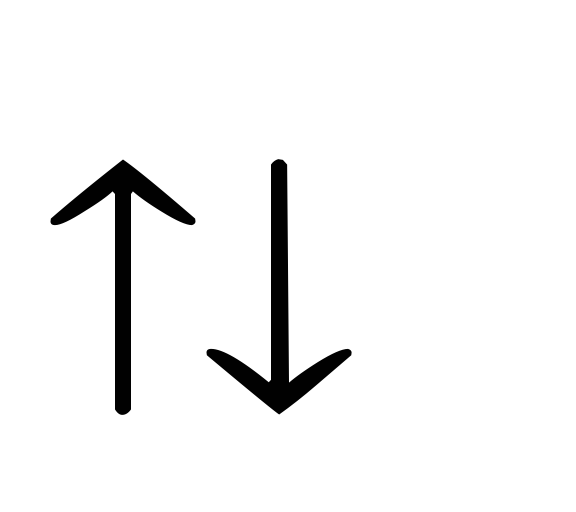
 .
.то
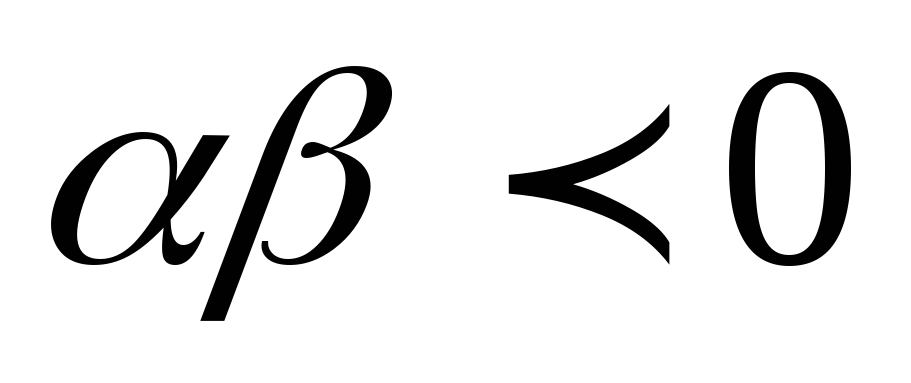 и
и
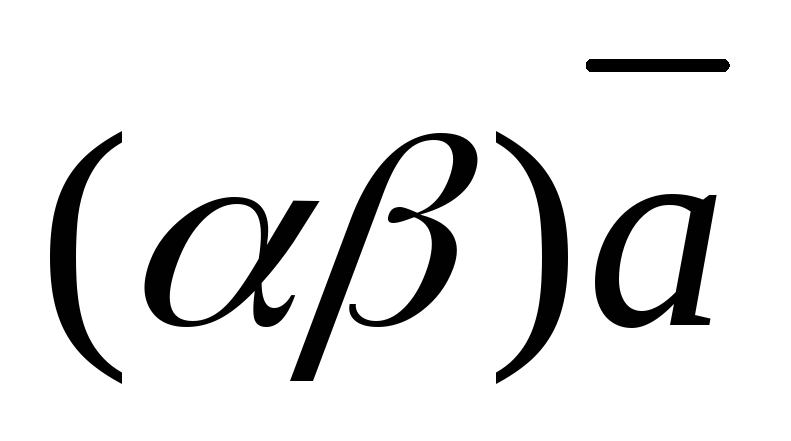
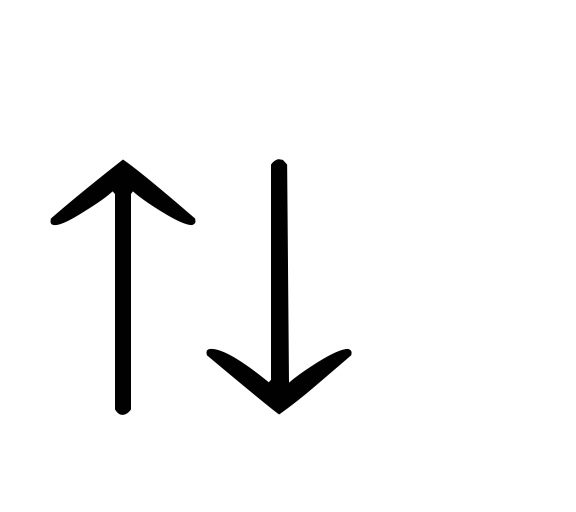
 ,
,т.е.
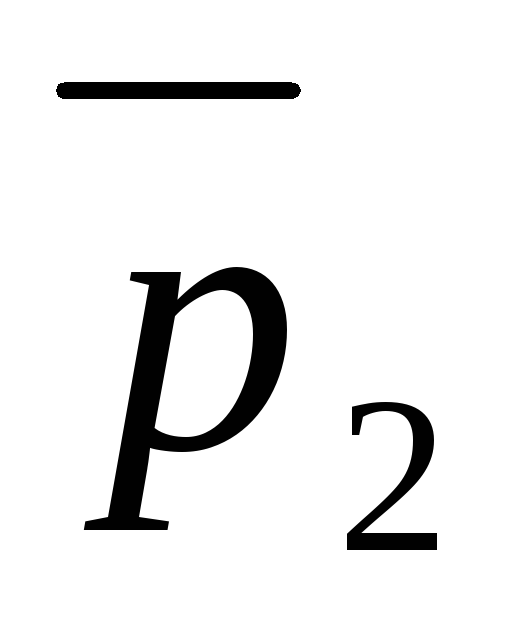
 .
.

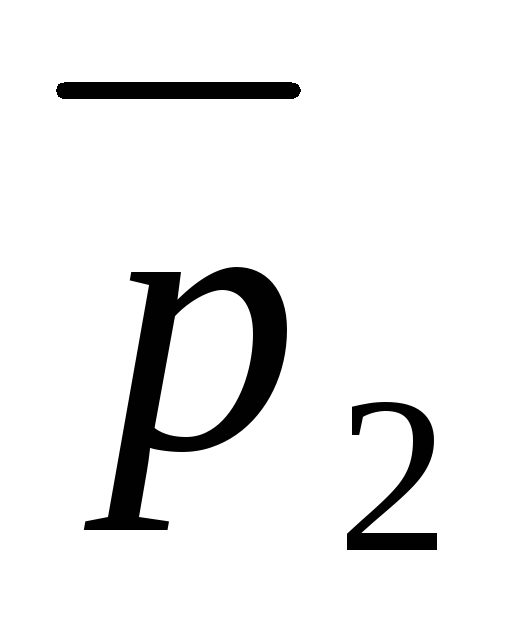
2.3) Если
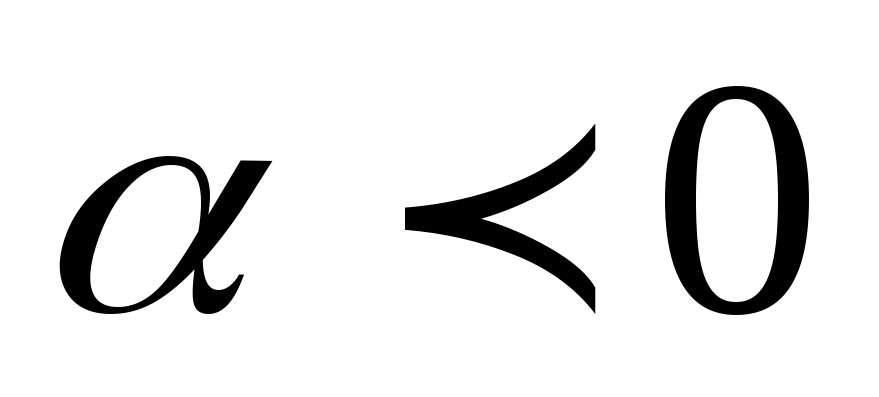 и
и
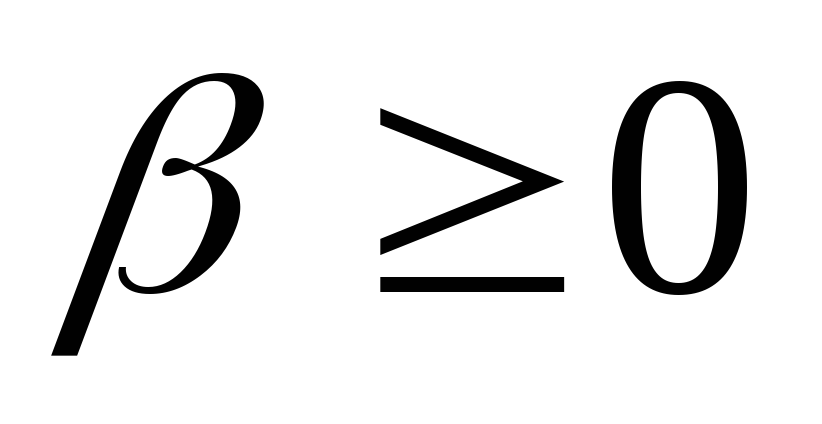 ,
,2.4) Если
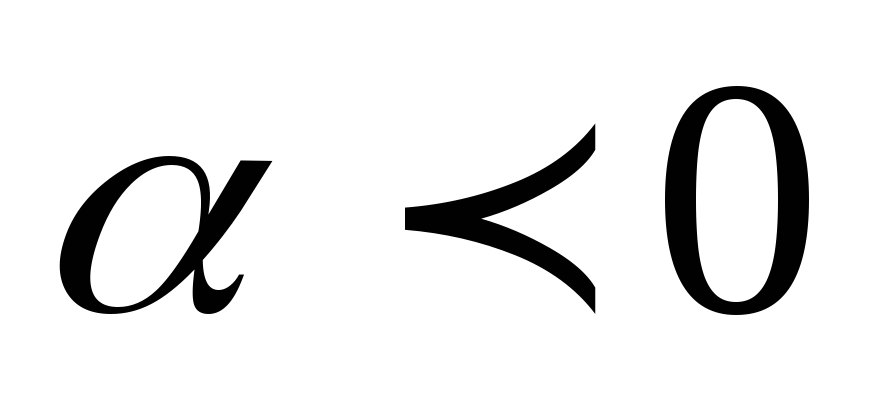 и
и
 ,
,Вывод
Так как 1)
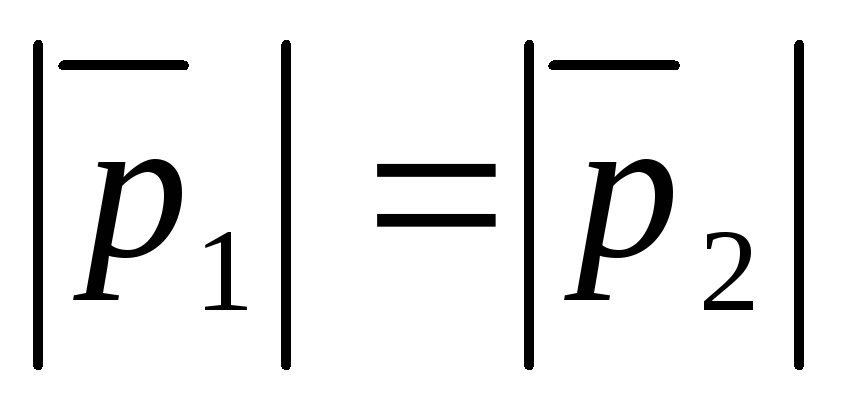 ;
2)
;
2) 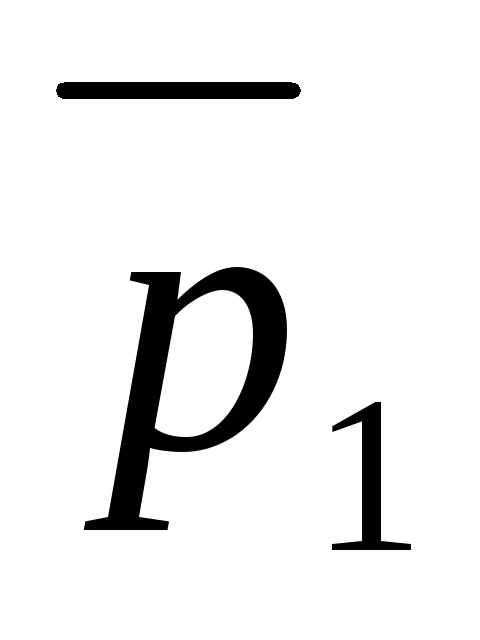

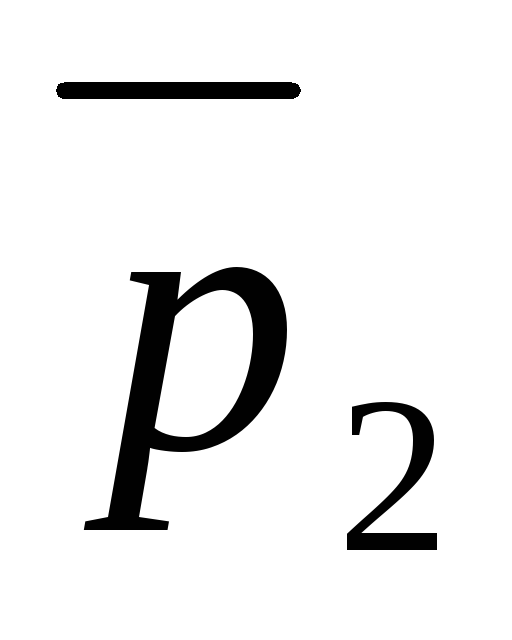 ,
то
,
то
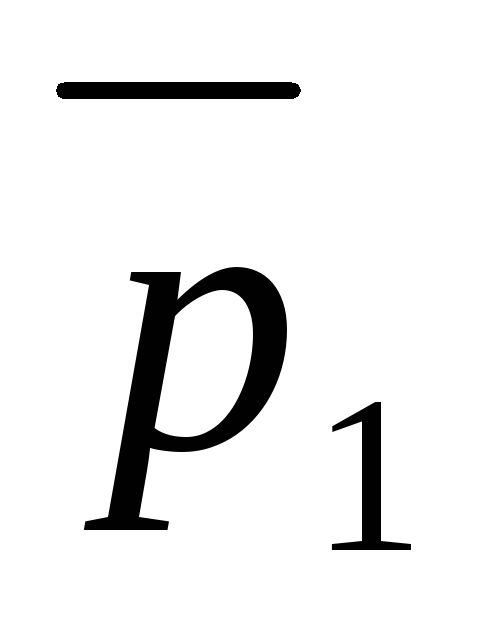 =
=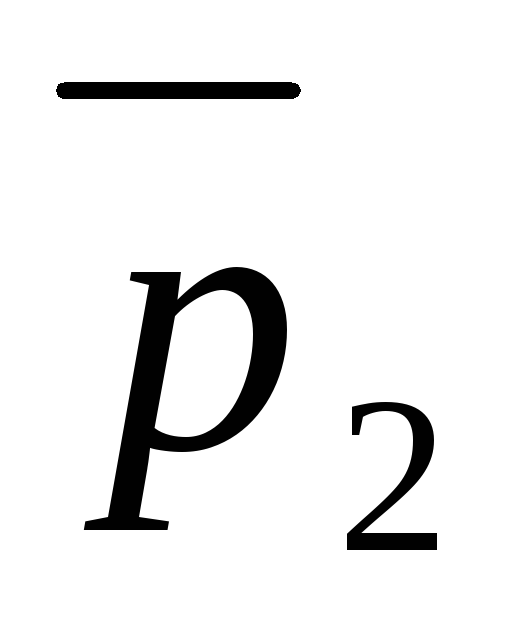 ,
т.е.
,
т.е.
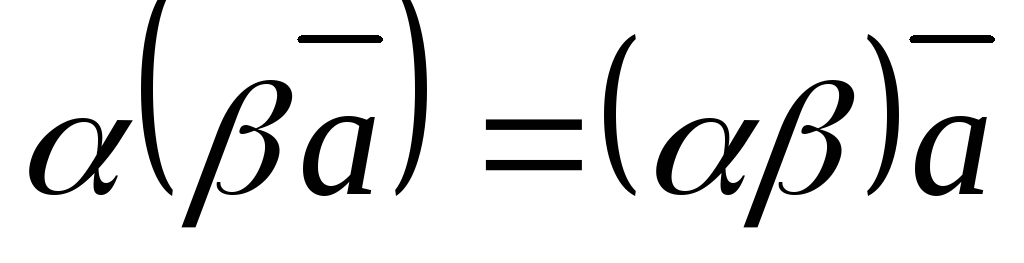 .
.
п. 2.3 и п.2.4 заполните самостоятельно. Докажите остальные свойства.
6. Векторное пространство
Мы выяснили, что
на множестве векторов (обозначим его
V3)
трехмерного пространства выполняются
свойств линейных операций, а именно: ![]() ,
R
,
R
1.
![]() 5.
5.
![]()
2.
![]() 6.
6.
![]()
3. ![]() /
/
![]() 7.
7.
![]()
4. –![]() /
/
![]() 8.
8.
![]() (7.4)
(7.4)
Говорят, что множество векторов V3 образует векторное пространство над полем R, в котором определено сложение векторов, умножение вектора на действительное число, удовлетворяющее свойствам 1–8, называемым системой аксиом векторного пространства.
Векторное пространство называется n-мерным (имеет размерность n), если в нем:
1) существует n линейно независимых векторов;
2) любая система n+1 векторов линейно зависима.
Обозначается: n=dim V или Vn.
Подмножество L векторного пространства V3 образует векторное подпространство, если оно само образует векторное пространство и удовлетворяет условиям:
1) ![]() ,
2)
,
2) ![]() . (7.5)
. (7.5)
