
- •Системы дифференциальных уравнений
- •1. Основные понятия
- •2. Интегрирование нормальных систем
- •3. Системы линейных дифференциальных уравнений с постоянными коэффициентами
- •Ипользование пакета mathcad при решении систем ду
- •Задания для лабораторной работы
- •Задания для лабораторной работы с ипользованием mathcad
- •Список литературы
3. Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим еще один метод интегрирования нормальной системы уравнений (1) в случае, когда она представляет собой систему линейных однородных ДУ с постоянными коэффициентами, т. е. систему вида

Для простоты ограничимся рассмотрением системы трех уравнений с тремя неизвестными функциями y1, y2 и y3:
 (5)
(5)
где все коэффициенты аi,j (i, j = 1,2,3) – постоянные. Будем искать частное решение системы (5) в виде
y1
=
![]() ,
y2
=
,
y2
=
![]() ,
y3
=
,
y3
=
![]() (6)
(6)
где а, β, γ, k – постоянные, которые надо подобрать (найти) так, чтобы функции (6) удовлетворяли системе (5).
Подставив эти
функции в систему (5) и сократив на
множитель
![]() ,
получим:
,
получим:

или
 (7)
(7)
Систему (7) можно рассматривать как однородную систему трех алгебраических уравнений с тремя неизвестными а, β, γ. Чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель системы был равен нулю:
 (8)
(8)
Уравнение (8) называется характеристическим уравнением, системы (5). Раскрыв определитель, получим уравнение третьей степени относительно k. Рассмотрим возможные случаи.
Случай 1. Корни характеристического уравнения действительны и различны: k1, k2, k3. Для каждого корня ki (i = 1,2,3) напишем систему (7) и определим коэффициенты аi, βi, γi (один из коэффициентов можно считать равным единице). Таким образом, получаем:
для корня k1
частное решение системы (5): y1(1)
=
![]() ,
y2(1)
= =
,
y2(1)
= =![]() ,
y3(1)
=
,
y3(1)
=
![]() ;
;
для корня k2
– y1(2)
=
![]() ,
y2(2)
=
,
y2(2)
=
![]() ,
y3(2)
= =
,
y3(2)
= =![]() ;
;
для корня k3
– y1(3)
=
![]() ,
y2(3)
=
,
y2(3)
=
![]() ,
y3(3)
= =
,
y3(3)
= =![]() .
.
Можно показать, что эти функции образуют фундаментальную систему, общее решение системы (5) записывается в виде
y1(1)
=c1![]() ,
y2(1)
= c2
,
y2(1)
= c2![]() ,
y3(1)
= c3
,
y3(1)
= c3![]() ,
,
y1(2)
= c1![]() ,
y2(2)
= c2
,
y2(2)
= c2![]() ,
y3(2)
= c3
,
y3(2)
= c3![]() ,
(9)
,
(9)
y1(3)
= c1![]() ,
y2(3)
= c2
,
y2(3)
= c2
![]() ,
y3(3)
= c3
,
y3(3)
= c3![]() .
.
Пример 3. Решить
систему уравнений
 .
.
Решение.
Характеристическое уравнение данной
системы имеет вид:
![]() ,
или 1 - 2k
+ k2
- 4 = 0, k2
- 2k
- 3 = =0, k1
= -1, k2
= 3. Частные
решения данной системы ищем в виде:
y1(1)
=
,
или 1 - 2k
+ k2
- 4 = 0, k2
- 2k
- 3 = =0, k1
= -1, k2
= 3. Частные
решения данной системы ищем в виде:
y1(1)
=![]() ,
y2(1)
=
,
y2(1)
=
![]() и y1(2)
=
и y1(2)
=
![]() ,
y2(2)
=
,
y2(2)
=
![]() .
Найдем αi
и β1
(i
= 1, 2). При k1
= -1 система (7) имеет вид:
.
Найдем αi
и β1
(i
= 1, 2). При k1
= -1 система (7) имеет вид:
 т.е.
т.е.
 Эта система имеет бесчисленное множество
решений. Положим α1
= =1, тогда β1
= 2. Получаем частные решения y1(1)
=
Эта система имеет бесчисленное множество
решений. Положим α1
= =1, тогда β1
= 2. Получаем частные решения y1(1)
=![]() ,
y2(1)
=
,
y2(1)
=
![]() .
При k2
= 3 система (7) имеет вид:
.
При k2
= 3 система (7) имеет вид:
 Положим α2
= 1, тогда β2
= -2. Значит, корню k2
= 3 соответствуют частные решения: y1(2)
=
Положим α2
= 1, тогда β2
= -2. Значит, корню k2
= 3 соответствуют частные решения: y1(2)
=
![]() ,
y2(2)
=
,
y2(2)
=
![]() .
Общее решение исходной системы, согласно
формуле (9), запишется в виде y1
=c1
.
Общее решение исходной системы, согласно
формуле (9), запишется в виде y1
=c1![]() +c2
+c2![]() ,
y2
= 2c1
,
y2
= 2c1![]() -2c2
-2c2![]() .
.
Случай 2. Корни характеристического уравнения различные, но среди них есть комплексные: k1 = а + ib, k2 = а - - ib, k3. Вид частных решений в этой ситуации определяют так же, как и в случае 1.
Замечание. Вместо полученных частных решений можно взять их линейные комбинации, применяя формулы Эйлера; в результате получим два действительных решения, содержащих функции вида еах·cos bx, eax·sin bx. Или, выделяя действительные и мнимые части в найденных комплексных частных решениях, получим два действительных частных решения (можно показать, что они тоже являются решениями уравнения). При этом понятно, что комплексно-сопряженный корень k2 = a - ib не даст новых линейно независимых действительных решений.
Случай 3. Характеристическое уравнение имеет корень k кратности т (т = 2,3). Решение системы, соответствующее кратному корню, следует искать в виде:
а) если т = 2, то у1 = (А + Вх)еkх, у2 = (С + Dx)ekx ,у3 = (Е + + Fx)ekx;
б) если т = 3, то У1 = (А + Вх + Сх2)еkх, у2 = (D + Ex + +Fx2)ekx, уз = (G + Hx + Nx2)ekx.
Это решение зависит от m произвольных постоянных. Постоянные А, В, С, ..., N определяются методом неопределенных коэффициентов. Выразив все коэффициенты через m из них, полагаем поочередно один из них равным единице, а остальные равными нулю. Получим т линейно независимых частных решений системы (5).
Пример 4. Решить
систему уравнений

Решение. Составляем
и решаем характеристическое уравнение
 ,
,
(1 - k)(2 -
2k - k + k2
-
1) - (-2 + k + 1) = 0, k1
= 2, k2
= k3
= 1. Корню
k1
= 2 соответствует система (см. (7)):
 или
или
 .
Полагая γ1
= 1, находим α1
= 1. Получаем одно частное решение исходной
системы:
y1(1)
=
.
Полагая γ1
= 1, находим α1
= 1. Получаем одно частное решение исходной
системы:
y1(1)
=
![]() ,
y2(1)
= 0, y3(1)
=
,
y2(1)
= 0, y3(1)
=
![]() .
.
Двукратному корню
k
= k2
= k3
= 1 (m
= 2) соответствует решение вида y1(2,3)=(А
+ Вх)ех,
y2(2,3)=(С
+ Dх)ех,
y3(2,3)=(E
+ +Fх)ех.
Подставляем эти выражения (решения) в
уравнения исходной системы
 или, после сокращения на ех
≠ 0 и
группировки,
или, после сокращения на ех
≠ 0 и
группировки,
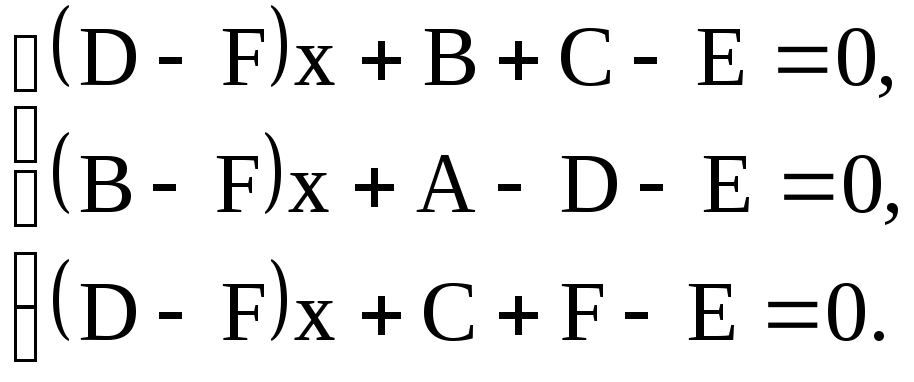
Эти равенства
тождественно выполняются лишь в случае,
когда

Выразим все коэффициенты через два из них (m = 2), например через А и В. Из второго уравнения имеем F = B. Тогда, с учетом первого уравнения, получаем D = B. Из четвертого уравнения находим E = A - D, т.е. E = A - B. Из третьего уравнения: C = E - B, C = A - 2 B. Коэффициенты A и B - произвольные.
Полагая А = 1, В = 0, находим: С = 1, D = 0, E = 1, F = 0.
Полагая А = 0, В = 1, находим: С = -2, D = 1, E = -1, F = 1.
Получаем два
линейно независимых частных решения,
соответствующих двукратному корню k
= 1: y1(2)
=
![]() ,
y2(2)
=
,
y2(2)
=
![]() ,
y3(2)
=
,
y3(2)
=
![]() и y1(3)
=
и y1(3)
=
![]() ,
y2(3)
=
,
y2(3)
=
![]() ,
y3(3)
=
,
y3(3)
=
![]() .
Записываем общее решение исходной
системы:
.
Записываем общее решение исходной
системы:
y1
= c1![]() +c2
+c2![]() + с3х
+ с3х![]() ,
,
y2
= c2![]() +c3(х
- 2)
+c3(х
- 2)![]() ,
,
y3
= c1![]() +c2
+c2![]() + с3(х
- 1)
+ с3(х
- 1)![]() .
.
