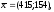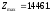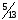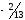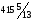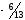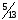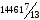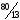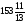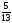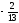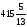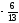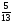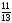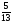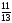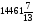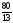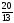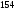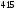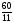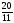12.2. Методы отсечения

Идея методов отсечения состоит в следующем. Решается задача ЛП, полученная из целочисленной задачи отбрасыванием условия целочисленности. Если решение вспомогательной задачи ЛП целочисленное, то оно же является и решением исходной задачи. Если оптимальное решение вспомогательной задачи не целочисленное, то к решённой задаче ЛП добавляют новое линейное ограничение; оно удовлетворяет целочисленным решениям исходной задачи, но не удовлетворяет полученному нецелочисленному решению первоначальной задаче ЛП. Указанное дополнительное линейное ограничение определяет некоторую отсекающую плоскость и называется правильным отсечением. Новые правильные отсечения добавляют к первоначальной вспомогательной задаче ЛП до тех пор, пока на некотором шаге не будет получено целочисленное решение вспомогательной задачи, являющееся, очевидно, оптимальным решением исходной задачи целочисленного линейного программирования.

Одним из методов отсечения является метод Гомори, названный так в честь своего автора (этот метод также носит название метода отсекающих плоскостей).

Решается задача полностью целочисленного линейного программирования:

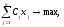
где

Наряду с ней рассматривается вспомогательная задача ЛП

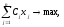
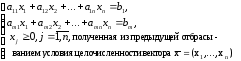(2)

Вспомогательная задача ЛП решается симплекс-методом. Пусть на последней итерации ограничения этой задачи приняли вид:

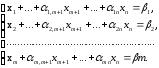
полученная из предыдущей отбрасыванием условия целочисленности вектора 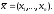Вспомогательная задача ЛП решается симплекс-методом. Пусть на последней итерации ограничения этой задачи приняли вид:

Как известно, оптимальным решением задачи будет вектор 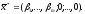Пусть существует номер i такой, что β_і – нецелое (в противном случае целочисленный вектор 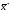является оптимальным решением и исходной задачи.

Обозначим, как обычно, [z] и {z} соответственно целую и дробную части числа z. Заметим, что если 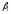– нецелое число, .

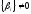Согласно общей идее метода отсечения необходимо перейти к решению новой вспомогательной задачи ЛП, у которой наряду с исходными ограничениями рассматривается дополнительное ограничение, осуществляющее правильное отсечение. Рассмотрим ограничение

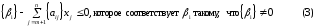
которое соответствует β_i такому, что {β_i}≠0. Имеет место следующее утверждение.

Теорема. Дополнительное линейное ограничение (3) является правильным отсечением для задачи целочисленного линейного программирования (1).

Рассмотрим алгоритм Гомори на примере:

Пример 12.1.

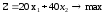
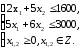
Решение. Сначала с помощью симплекс-метода решим вспомогательную задачу нецелочисленного линейного программирования.

Запишем данную задачу в каноническом виде:

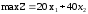
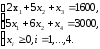
Начальная симплексная таблица имеет вид:

БП	Сб	Ао	x1		x2		x3	x4
			20		40		0	0
x3	0	1600	2		[5]		1	0
x4	0	3000	5		6		0	1
Zj - Cj		0		-20		-40	0		0

БП	Сб	Ао	x1		x2		x3	x4
			20		40		0	0
x2	40	320	2/5		1		1/5	0
x4	0	1080	[13/5]		0		-6/5	1
Zj - Cj		12800		-4		0	8		0

БП	Сб	Ао	x1	x2		x3		x4
			20	40		0		0
x2	40		0	1
x1	20		1	0
Zj - Cj			0		0

Эта таблица содержит оптимальный план нецелочисленной задачи ЛП.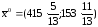. Данное решение не может быть решением целочисленной задачи, поэтому необходимо перейти к следующему этапу.

Среди дробных частей найденного решения выберем наибольшую. И это 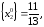так как .

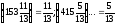Так, что строка последней симплексной таблицы, отвечающая переменной 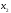_, поможет построить дополнительное линейное ограничение

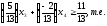
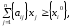
где 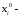переменная оптимального решения, имеющая наибольшую дробную часть,

число, стоящее в строке переменной 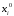в последней симплексной таблице

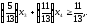
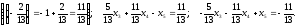
Допишем полученное ограничение в последнюю симплекс таблицу. Получим новую таблицу:

БП	Сб	Ао		x1	x2		x3		x4		x5
				20	40		0		0		0
x2	40			0	1						0
x1	20			1	0						0
x5	0	-		0	0		-		-		1
Zj - Cj				0		0					0

Чтобы затем решить данную задачу (в столбике А₀ появилось отрицательное число) нужно выполнить следующие операции.

1). Рассмотрим строку, содержащую отрицательное число в столбце А₀, и выберем какое- либо отрицательное число в этой строке. Выбранное число стоит в столбце переменной, которую нужно ввести в базис.

2). Для чисел с одинаковыми знаками составляем симплексные отношения.

3). Наименьшее симплексное отношение определяет ту переменную, которую выводим из базиса.

4). Составляем новую таблицу, выполняя симплексные преобразования.

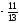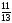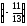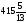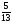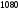В нашей задаче, в строке переменной x₅ возьмём число , для данного столбца найдём симплексные отношения. -: =1; := наименьшее симплексное отношение 1. Таким образом, вместо переменной x₅ введём переменную x_4.

БП	Сб	Ао	x1	x2		x3		x4	x5
			20	40		0		0	0
x2	40
x1	20
x5	0
Zj - Cj			0		0			0

Имеем оптимальное целочисленное решение расширенной задачи. Тогда оптимальное решение исходной задачи, учитывая ограничения (1),