§ 5. Корни из единицы.

1 = cos0+i sin0 = cos+i sin, .

Корни расположены на окружности единичного радиуса и делят эту окружность на n равных частей.

Теорема 1.

Все значения корня n–той степени из комплексного числа z можно получить умножением одного из них на все корни из 1.

Доказательство:

Возьмём  = = (cos+i sin), где s–фиксированное число.

₁, ₂,…, _n – так обозначим все корни .

Домножим каждый из корней ₁,…, _n на . Они разные, все являются корнями n–той степени из z, ибо (_i)ⁿ = z и их штук.

Теорема доказана.

Теорема 2.

Произведение двух корней n–той степени из единицы есть корень степени n из единицы.

Следствие.

Степень корня n–той степени из единицы есть корень степени n из единицы.

Все ли корни из 1 равноправны?

n=4 ; 1, –1, i, –i — корни из единицы.

i; –i — первообразные корни; если i возводить в степени 0, 1, 2, 3, то получим все корни.

Определение 1.

Корень n–той степени из 1 называется первообразным, если он не даёт единицу в степени меньше, чем n.

Всегда ли есть первообразный корень?

Всегда! Например: cos+i sin.

Упражнение. Доказать, что корень n–той степени

_k = cos + i sin будет первообразным, если n и k — взаимно простые (не имеют общих делителей отличных от 1).

§6. Числовое поле.

В множествах Q  R  C возможны четыре операции +, –, , .

Определение 1. Подмножество K  C множества комплексных чисел C, состоящее более, чем из одного элемента, называют числовым полем, если выполняются следующие условия:

1)  a, bK  a+bK , то есть в множестве K всегда возможно сложение;

2.  aK  –aK ;

3.  a, bK  abK , то есть задано умножение в K (K замкнуто относительно умножения);

4)  a  0 ; a ^-1K.

Из 2) с учётом 1) получаем, что в K всегда возможно вычитание.

Из 4) с учётом 3) получаем, что в K всегда возможно деление на число не равное 0.

Q — поле рациональных чисел;

R — поле вещественных чисел;

C — поле комплексных чисел.

Упражнение 1. Числовое поле всегда бесконечно. Упражнение 2. Любое числовое поле всегда содержит q (множество рациональных чисел).

Пример поля отличного от Q, R и C:

K = {a+b, где a и b }.

Тема 2. Матрицы и определители.

§1. Сложение матриц. Умножение матрицы на число.

Пусть К ≠ . Рассмотрим прямоугольную таблицу из n строк и m столбцов, состоящую из элементов К

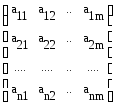
(1)

a_ij — произвольный элемент таблицы, где i — номер строки, j — номер столбца, a_ij  К  i,j. Таблицу (1) назовем матрицей размером n x m. Краткая запись (a_ij)_{n x m.} В будущем будем рассматривать (1) над числовыми полями. Матрицы будем обозначать A,B,C, а их элементы соответственно a_ij , b_ij, c_ij .

Определение 1. Две матрицы (a_ij), (b_ij ) одинаковых размеров будем называть равными, если a_ij = b_ij  i,j.

Определение 2. Матрица называется квадратной, если m=n.

Определение 3. Квадратная матрица называется диагональной, если все элементы, стоящие вне главной диагонали, равны 0.

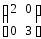Пример:

Определение 4. Диагональная матрица, все элементы которой равны между собой, называется скалярной матрицей.

Скалярная матрица, у которой элемент, стоящий на диагонали равен 1, называется единичной.

Пример: