
1. Определение опорных реакций
Опора А
– шарнирно-неподвижная. Допустим, что
реакция
![]() направлена вверх, а реакция
направлена вверх, а реакция
![]() вправо.
вправо.
Опора В
– шарнирно-подвижная, допустим, что
реакция
![]() тоже направлена вверх.
тоже направлена вверх.
Для определения
![]() ,
,
![]() ,
,
![]() составим три уравнения статики:
составим три уравнения статики:
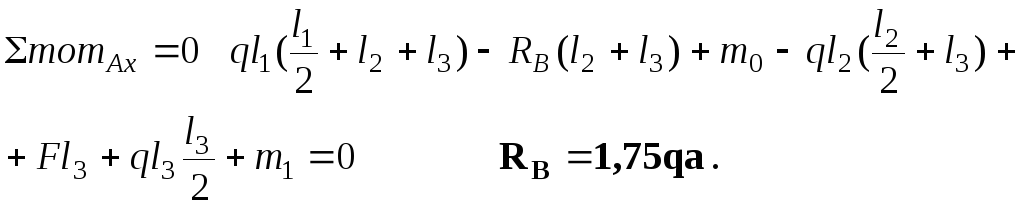
Реакция
![]() получилась положительной, следовательно,
наше допущение, что она направлена
вверх, верно.
получилась положительной, следовательно,
наше допущение, что она направлена
вверх, верно.
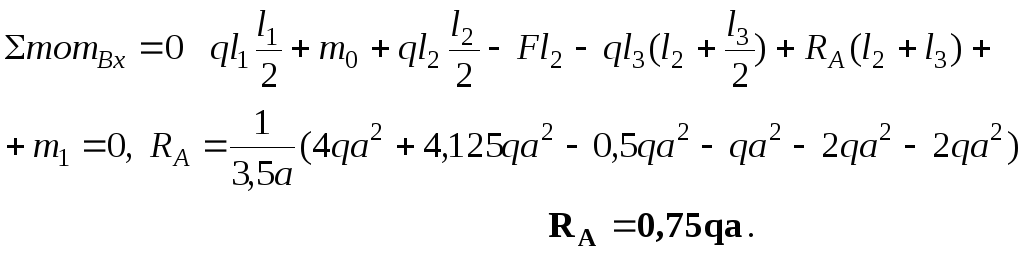
![]() Отсюда
Отсюда
![]() .
.
Проверка:
![]()
Итак:
![]()
2. Построение эпюр внутренних сил
В соответствии с
характером конструкции и нагрузки делим
балку на три участка. Эпюры будем строить
по участкам.
![]() и
и
![]() будем определять методом сечений с
использованием формул (1) или (2).
будем определять методом сечений с
использованием формул (1) или (2).
I
участок.
Проведем сечение в пределах участка.
Видно, что выгоднее рассмотреть левую
отсеченную часть. Тогда сечение определим
текущей координатой
![]() .
Согласно формул (1) получим
.
Согласно формул (1) получим
![]() линейная зависимость,
линейная зависимость,
![]() по закону квадратной
параболы.
по закону квадратной
параболы.
Для построения
эпюр
![]() и
и
![]() на этом участке подсчитаем величины
на этом участке подсчитаем величины
![]() и
и
![]() при следующих значениях координаты
при следующих значениях координаты
![]() :
:
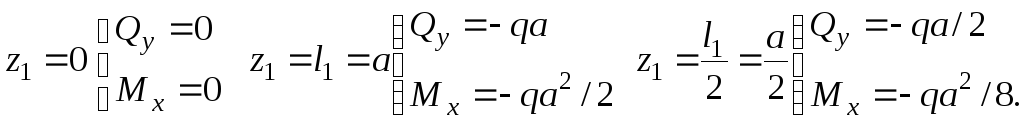
Строим эпюры
![]() и
и
![]() на этом участке, откладывая в масштабе
положительные значения
на этом участке, откладывая в масштабе
положительные значения
![]() и
и
![]() вниз, а отрицательные – вверх от оси
бруса.
вниз, а отрицательные – вверх от оси
бруса.
II
участок.
Рассмотрим левую отсеченную часть
![]()
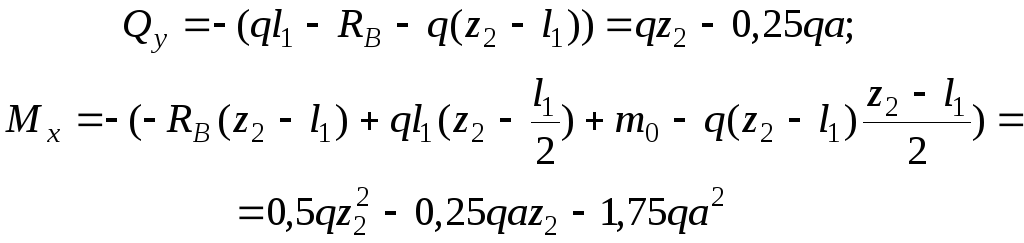
при
 ;
при
;
при
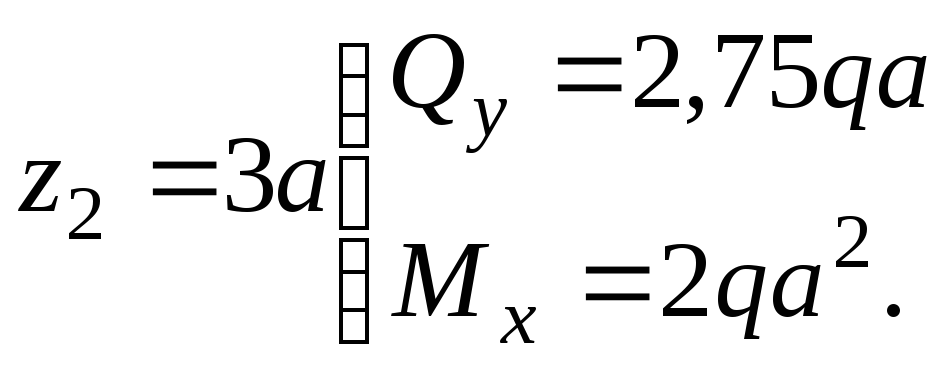
Строим эпюры
![]() и
и
![]() на этом участке, учитывая, что для
построения
на этом участке, учитывая, что для
построения
![]() достаточно двух значений (линейная
зависимость), а для построения
достаточно двух значений (линейная
зависимость), а для построения
![]() необходимо не менее трех значений
необходимо не менее трех значений
![]() в пределах участка (парабола). Надо
дополнительно вычислить
в пределах участка (парабола). Надо
дополнительно вычислить
![]() при
при
![]() .
.
III
участок.
Проводим сечение, видно, что выгоднее
рассмотреть правую отсеченную часть.
В этом случае текущую координату сечения
![]() будем отсчитывать от опоры А
будем отсчитывать от опоры А
![]() .
По формулам (2):
.
По формулам (2):
![]() (А)
(А)
при
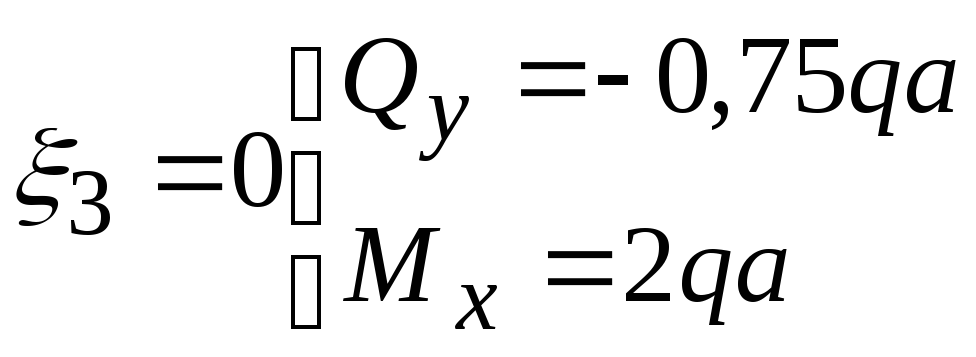 ;
при
;
при
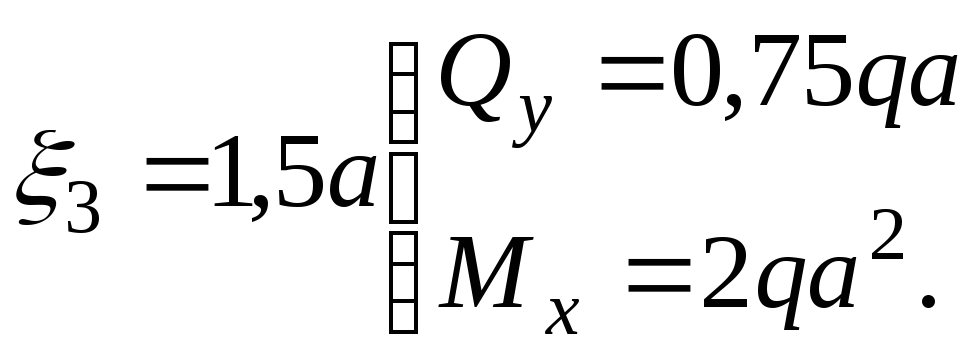
Видно, что при
некотором значении
![]() эпюра
эпюра
![]() меняет знак. В этом сечении величина
меняет знак. В этом сечении величина
![]() принимает экстремальное значение.
принимает экстремальное значение.
Подставим в первую
формулу (А)
![]() при
при
![]() ,
получим
,
получим
![]() .
Отсюда
.
Отсюда
![]() .
Подставим
.
Подставим
![]() во вторую формулу (А),
найдем
во вторую формулу (А),
найдем
![]() .
.
Строим эпюры
![]() и
и
![]() на третьем участке. На эпюрах ставим
знаки, характерные величины
на третьем участке. На эпюрах ставим
знаки, характерные величины
![]() и
и
![]() ,
штриховка эпюр ведется линиями,
перпендикулярными к оси бруса.
,
штриховка эпюр ведется линиями,
перпендикулярными к оси бруса.
3. Проверка построенных эпюр
а) По зависимости
![]() проверяются
проверяются
![]() и
и
![]() .
.
I
участок: В
произвольном сечении
![]() на эпюре
на эпюре
![]() проведем касательную. Угол ее наклона
к оси
проведем касательную. Угол ее наклона
к оси
![]() обозначим
обозначим
![]() .
Видно, что
.
Видно, что
![]() ,
с увеличением
,
с увеличением
![]()
![]() уменьшается. В этом же сечении
уменьшается. В этом же сечении
![]() и с увеличением
и с увеличением
![]()
![]() уменьшается. Следовательно, на I
участке эпюры
уменьшается. Следовательно, на I
участке эпюры
![]() и
и
![]() соответствуют зависимости
соответствуют зависимости
![]() .
.
II
участок:
![]() ,
с увеличением
,
с увеличением
![]()
![]() увеличивается.
увеличивается.
![]() ,
с увеличением
,
с увеличением
![]()
![]() увеличивается. Следовательно, эпюры
увеличивается. Следовательно, эпюры
![]() и
и
![]() соответствуют друг другу.
соответствуют друг другу.
III
участок:
Выделим сечение на участке
![]() .
Видно, что
.
Видно, что
![]() ,
с уменьшением
,
с уменьшением
![]()
![]() уменьшается до нуля при
уменьшается до нуля при
![]() ,
а затем принимает отрицательные значения.
,
а затем принимает отрицательные значения.
![]() ,
с уменьшением
,
с уменьшением
![]() уменьшается до нуля при
уменьшается до нуля при
![]() ,
а затем
,
а затем
![]() становится.
становится.
Итак, эпюры
![]() и
и
![]() на всем протяжении балки не противоречат
зависимости
на всем протяжении балки не противоречат
зависимости
![]() .
.
б) По зависимости
![]() проверяется эпюра
проверяется эпюра
![]() с действующей на балку нагрузкой
с действующей на балку нагрузкой
![]() .
.
I
участок: В
произвольном сечении
![]() на эпюре
на эпюре
![]() проведем касательную. Угол ее наклона
к оси
проведем касательную. Угол ее наклона
к оси
![]() обозначим
обозначим
![]() .
Видно, что
.
Видно, что
![]() ,
с увеличением
,
с увеличением
![]()
![]() .
На этом участке на балку действует
постоянная нагрузка
.
На этом участке на балку действует
постоянная нагрузка
![]() (вниз). Следовательно,
(вниз). Следовательно,
![]() есть величина отрицательная и постоянная,
что соответствует характеру изменения
есть величина отрицательная и постоянная,
что соответствует характеру изменения
![]() на этом участке. Итак, на I
участке противоречий нет.
на этом участке. Итак, на I
участке противоречий нет.
II
участок:
![]() ,
с увеличением
,
с увеличением
![]() не меняется. На этом участке действует
не меняется. На этом участке действует
![]() (вверх), т.е.
(вверх), т.е.
![]() и постоянная на этом участке. Противоречий
нет.
и постоянная на этом участке. Противоречий
нет.
III
участок:
![]() ,
с уменьшением
,
с уменьшением
![]() не меняется. На этом участке действует
не меняется. На этом участке действует
![]() (вниз), т.е.
(вниз), т.е.
![]() и постоянна.
и постоянна.
Итак, на всем
протяжении балки эпюра
![]() соответствует зависимости
соответствует зависимости
![]() .
.
в) При движении
вдоль оси
![]() балки:
балки:
На эпюре
![]() в сечении В
скачок от 1
до
в сечении В
скачок от 1
до
![]() ,
т.е. на величину
,
т.е. на величину
![]() ,
в этом сечении на балку действует
,
в этом сечении на балку действует
![]() ;
в сечении С
на эпюре
;
в сечении С
на эпюре
![]() скачок от
скачок от
![]() до
до
![]() ,
т.е. на величину
,
т.е. на величину
![]() ,
в этом сечении действует сила
,
в этом сечении действует сила
![]() ;
в сечении А
на эпюре
;
в сечении А
на эпюре
![]() скачок от
скачок от
![]() до нуля, в этом сечении на балку действует
сила
до нуля, в этом сечении на балку действует
сила
![]() .
.
Итак, скачки на
эпюре
![]() по величине соответствует локальным
поперечным силам, действующим на балку.
по величине соответствует локальным
поперечным силам, действующим на балку.
На эпюре
![]() скачок в сечении В
от
скачок в сечении В
от
![]() до
до
![]() ,
т.е. на величину
,
т.е. на величину
![]() ,
в этом сечении на балку действует
,
в этом сечении на балку действует
![]() ;
в сечении А
на эпюре
;
в сечении А
на эпюре
![]() скачок от
скачок от
![]() до нуля, в этом сечении на балку действует
момент
до нуля, в этом сечении на балку действует
момент
![]() .
Больше скачков нет и нет других локальных
моментов на балке.
.
Больше скачков нет и нет других локальных
моментов на балке.
Пример №2. Балка с промежуточным шарниром (рис. 1)
Дано: ![]() кН/м,
кН/м,
![]() м
м
В сечении А
– защемление, опорные реакции обозначим
так:
![]() вверх,
вверх,
![]() влево,
влево,
![]() против хода часовой стрелки. На опоре
В
реакцию
против хода часовой стрелки. На опоре
В
реакцию
![]() направим вверх. Опорных реакций четыре:
направим вверх. Опорных реакций четыре:
![]()
![]() ,
а уравнений три. Учитывая, что в точке
,
а уравнений три. Учитывая, что в точке
![]() балки расположен шарнир, можно составить
дополнительные уравнения равновесия
балки расположен шарнир, можно составить
дополнительные уравнения равновесия
![]() для левой или правой частей балки
относительно шарнира.
для левой или правой частей балки
относительно шарнира.
Справа от шарнира
только одна реакция
![]() ,
поэтому для ее определения рассмотрим
равновесие правой части балки относительно
шарнира
,
поэтому для ее определения рассмотрим
равновесие правой части балки относительно
шарнира
![]()
![]()
![]() .
.
Реакция
![]() получилась отрицательная, следовательно,
ее действительное направление
противоположно ранее принятому. Для
удобства дальнейших расчетов обычно
на схеме балки исправляют направление
реакции. Итак, действительная реакция
направлена вниз и ее величина
получилась отрицательная, следовательно,
ее действительное направление
противоположно ранее принятому. Для
удобства дальнейших расчетов обычно
на схеме балки исправляют направление
реакции. Итак, действительная реакция
направлена вниз и ее величина
![]() .
В дальнейших расчетах будем пользоваться
действительным направлением реакции
.
В дальнейших расчетах будем пользоваться
действительным направлением реакции
![]() .
.
Оставшиеся реакции найдем из уравнений статики для всей балки:

Рис.2
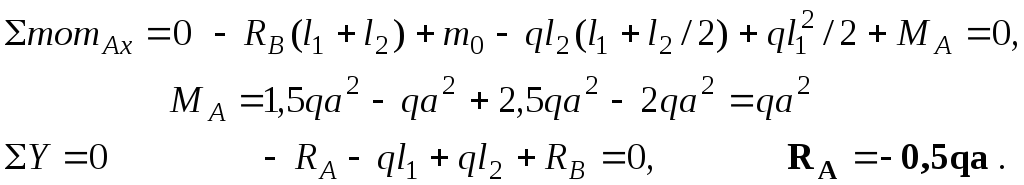
Реакция
![]() получилась отрицательной, следовательно,
ее действительное направление вниз.
Делаем исправление на схеме, тогда
получилась отрицательной, следовательно,
ее действительное направление вниз.
Делаем исправление на схеме, тогда
![]() .
.
![]() .
.
Проверка: ![]()
Итак:
![]() (вниз),
(вниз),
![]() (вниз),
(вниз),
![]()
I
участок
![]() (левая отсеченная часть)
(левая отсеченная часть)
![]()
при
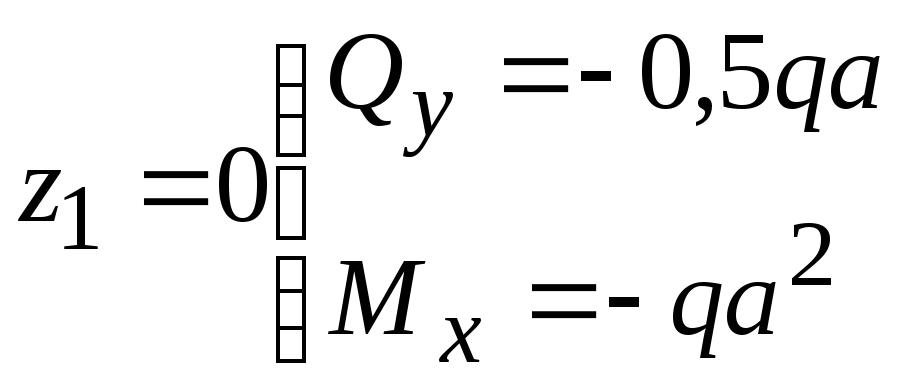 ;
при
;
при
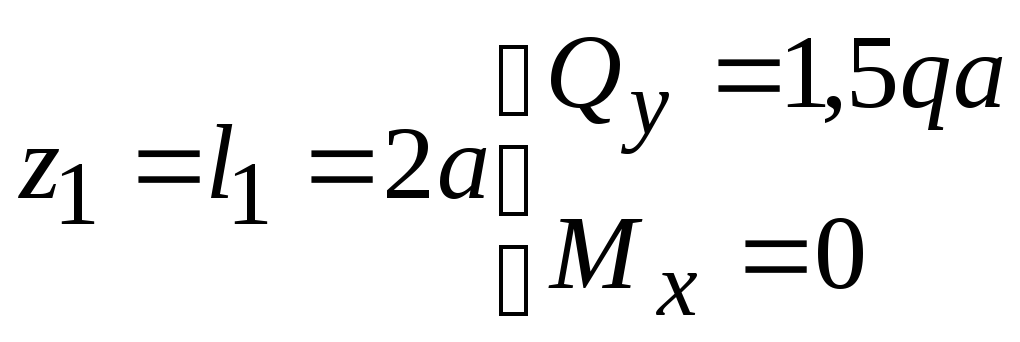
Эпюра
![]() меняет знак. Найдем
меняет знак. Найдем
![]() ,
где
,
где
![]() и
и
![]()
![]()
при
![]()
![]() .
.
Строим эпюры
![]() и
и
![]() на этом участке.
на этом участке.
II
участок:
![]() (правая отсеченная часть)
(правая отсеченная часть)
![]()
при
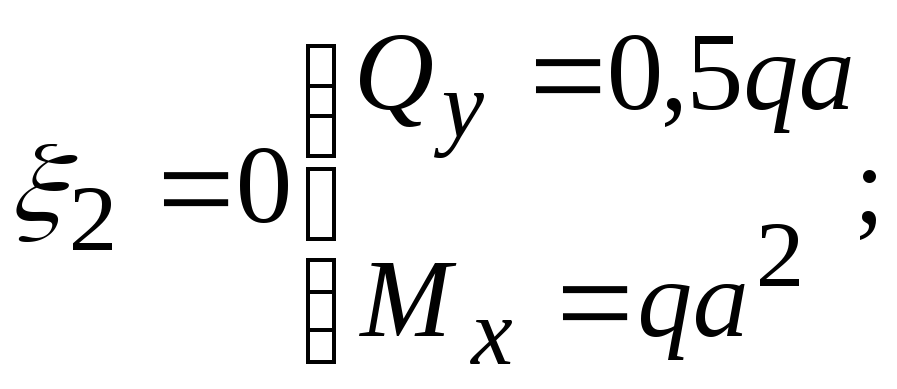 при
при
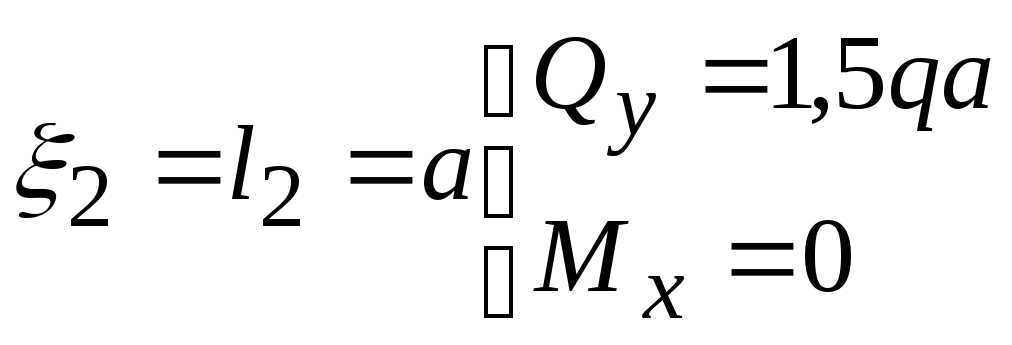
Строим по этим
данным эпюры
![]() и
и
![]() на II
участке. Надо дополнительно вычислить
на II
участке. Надо дополнительно вычислить
![]() при
при
![]() ,
т.к. эпюра
,
т.к. эпюра
![]()
парабола.
парабола.
Пример №3. Рама (рис. 2)
Дано: ![]() кН,
кН,
![]() кНм,
кНм,
![]() кН/м,
кН/м,
![]() м,
м,
![]() м
м
![]() м
м
Опора А
– шарнирно-неподвижная. Обозначим
![]() –вверх,
–вверх,
![]() влево. Опора В
– шарнирно-подвижная, обозначим
влево. Опора В
– шарнирно-подвижная, обозначим
![]() – вверх.
– вверх.

Рис.3
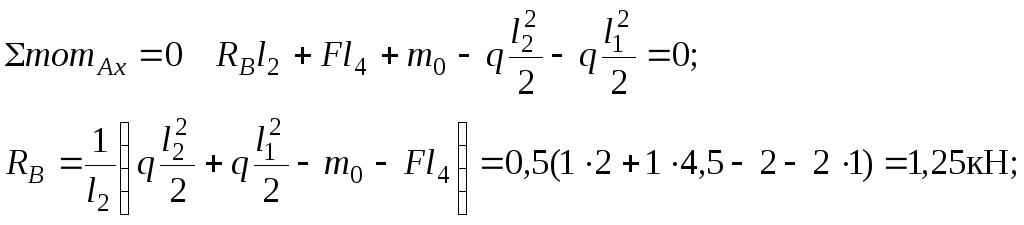
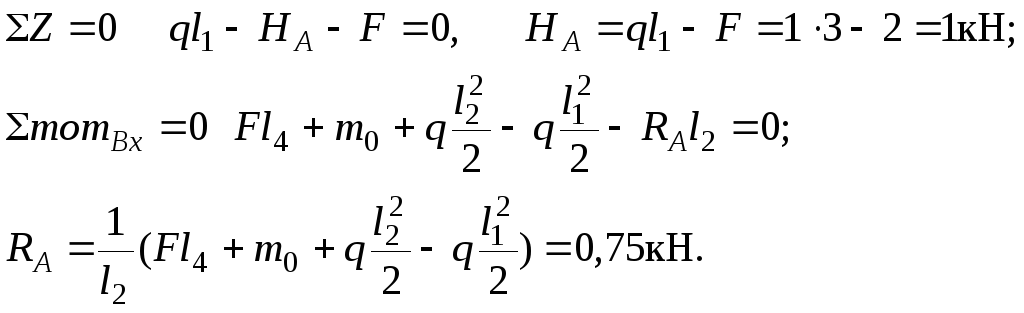
Все направления реакций, указанные на рис.2, являются действительными.
Проверка:
![]() .
.
По характеру
конструкции и нагрузки раму разделим
на четыре участка:
![]() .
Для каждого участка вводим свою систему
координат
.
Для каждого участка вводим свою систему
координат
![]() ,
которые получим простым перемещением
оси
,
которые получим простым перемещением
оси
![]() правой системы координат
правой системы координат
![]() вдоль оси стержней рамы.
вдоль оси стержней рамы.
На I
участке
![]() ось
ось
![]() направим от т.А
к т.
направим от т.А
к т.
![]() (см. рис. 2), ось
(см. рис. 2), ось
![]() (на нас) и
(на нас) и
![]() составляют с осью
составляют с осью
![]() правую систему координат. Проводим
сечение. Видно, что выгоднее рассматривать
нижнюю отсеченную часть, что в осях
правую систему координат. Проводим
сечение. Видно, что выгоднее рассматривать
нижнюю отсеченную часть, что в осях
![]() будет левой отсеченной частью.
будет левой отсеченной частью.
Итак: I
участок,
![]() (левая часть). Согласно формуле (1) получим
зависимости для внутренних сил:
(левая часть). Согласно формуле (1) получим
зависимости для внутренних сил:
![]()
при
 при
при
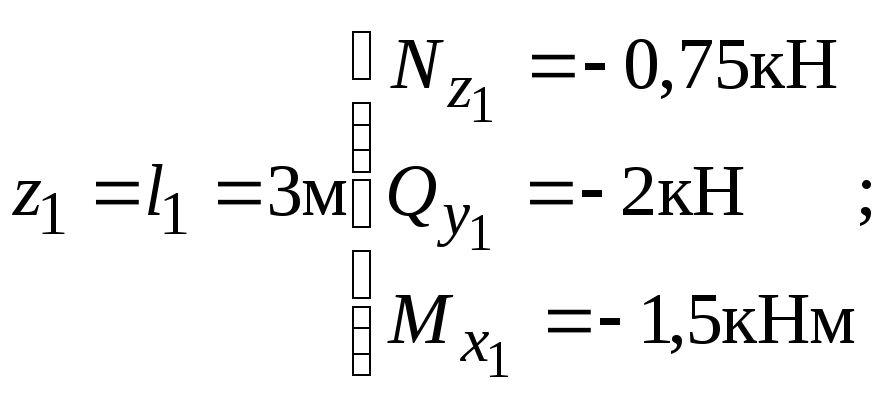
Эпюра
![]() меняет знак при
меняет знак при
![]() =1 м. В этом сечении
=1 м. В этом сечении
![]() кНм
кНм
На II
участке
![]() ось
ось
![]() направим от т.
направим от т.
![]() к т.Е,
ось
к т.Е,
ось
![]() вниз.
Проведем сечение и рассмотрим часть
рамы слева от сечения:
вниз.
Проведем сечение и рассмотрим часть
рамы слева от сечения:
![]() (левая часть);
(левая часть);
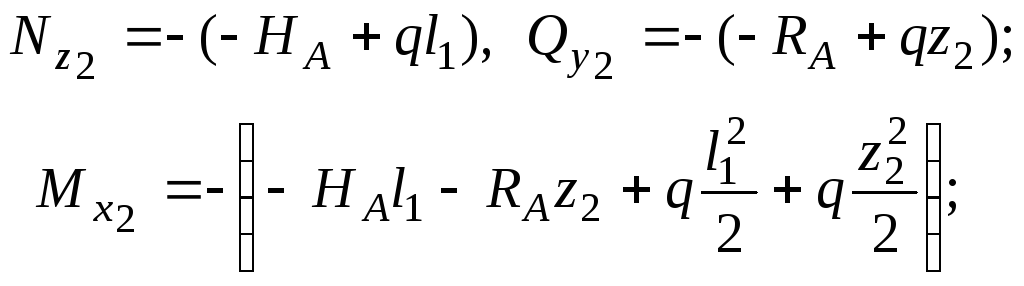
при
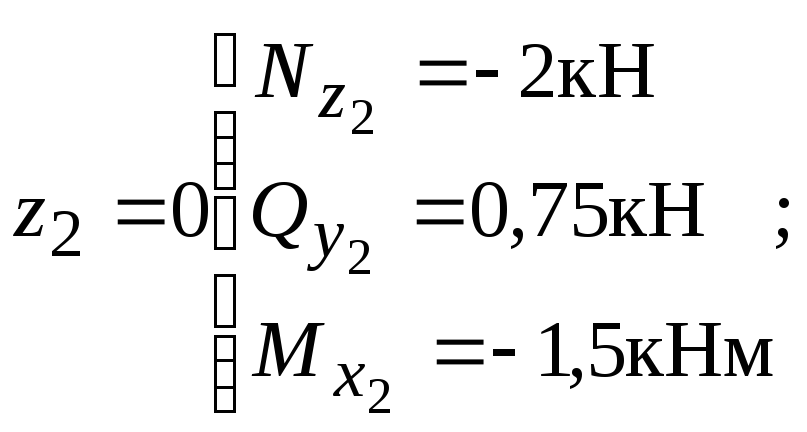 при
при
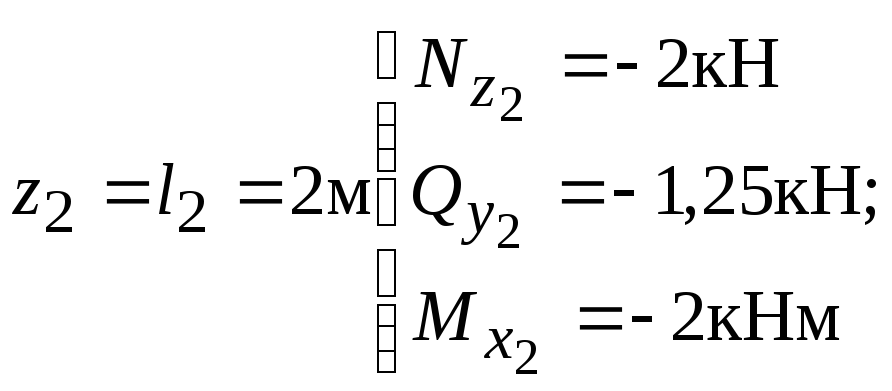
Эпюра
![]() меняет знак. Найдем
меняет знак. Найдем
![]() ,
где
,
где
![]() =0
и
=0
и
![]()
![]() м
м
при
![]()
![]() кНм.
кНм.
Строим теперь
эпюры
![]() и
и
![]() на этом участке.
на этом участке.
III
участок
![]() .
Ось
.
Ось
![]() направим от т. Е
до т. С,
ось у3
– влево. Проведем сечение и рассмотрим
нижнюю часть. Положение сечения определим
текущей координатой
направим от т. Е
до т. С,
ось у3
– влево. Проведем сечение и рассмотрим
нижнюю часть. Положение сечения определим
текущей координатой
![]() ,
при этом
,
при этом
![]() .
В осях
.
В осях
![]() рассматриваемая часть будет правой. По
формулам (2) получим следующие выражения
для внутренних сил:
рассматриваемая часть будет правой. По
формулам (2) получим следующие выражения
для внутренних сил:
![]()
при
 при
при
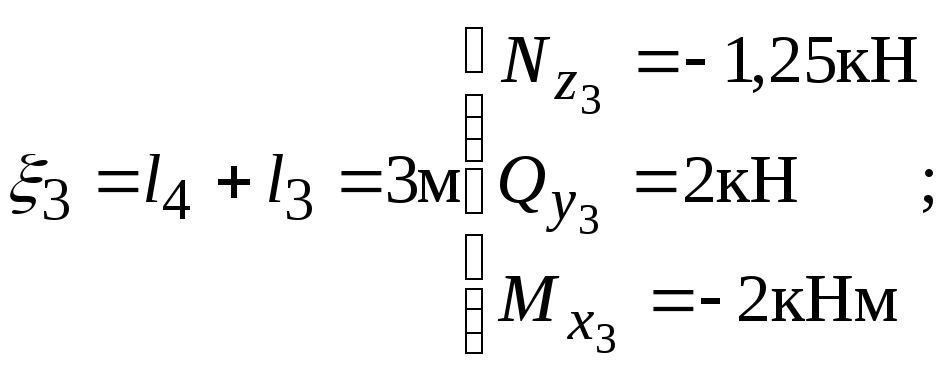
По этим данным
строим эпюры
![]() ,
,
![]() на III
участке.
на III
участке.
IV
участок CB.
Определение
внутренних сил проводится аналогично
как и для III
участка:
![]() (правая часть).
(правая часть).
![]() .
.
Так как внутренние
усилия не зависят от текущей координаты
![]() ,
сразу строим эпюры на этом участке. На
эпюрах ставим знаки и делаем штриховку
перпендикулярно к осям стержней рамы.
,
сразу строим эпюры на этом участке. На
эпюрах ставим знаки и делаем штриховку
перпендикулярно к осям стержней рамы.
Пример №4.
Криволинейный брус радиуса
![]() (рис. 3)
(рис. 3)
Дано: ![]() 4кН,
4кН,
![]() 2кН,
2кН,
![]() кНм,
кНм,
![]() м
м
Выберем на брусе
произвольную т.![]() .
Ее положение определим угловой координатой
.
Ее положение определим угловой координатой
![]() ,
при этом координата
,
при этом координата
![]() этой точки будет равна
этой точки будет равна
![]() .
Проведем поперечное сечение в т.
.
Проведем поперечное сечение в т.![]() и рассмотрим левую
отсеченную часть,
где известны нагрузки
и рассмотрим левую
отсеченную часть,
где известны нагрузки
![]() .
В этом
.
В этом
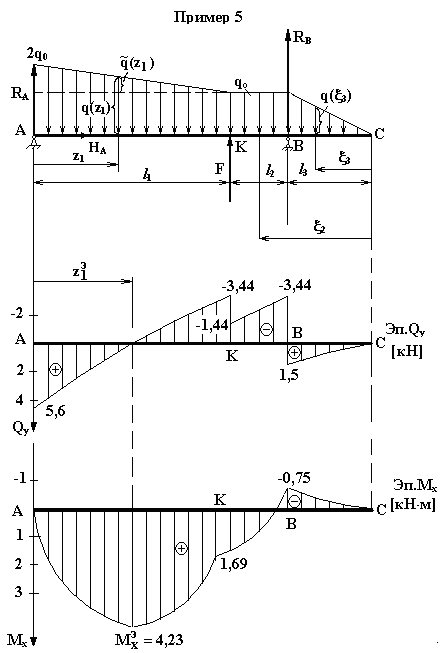
Рис.4
случае не надо
определять опорные реакции. В сечении
расположим начало системы координат
![]() ,
причем ось
,
причем ось
![]() направим по касательной к оси бруса в
т.
направим по касательной к оси бруса в
т.![]() в наружную сторону от торца левой
отсеченной части, ось
в наружную сторону от торца левой
отсеченной части, ось
![]() к центру кривизны. Согласно ранее
введенным правилам на торце левой части
покажем положительные направления
внутренних сил
к центру кривизны. Согласно ранее
введенным правилам на торце левой части
покажем положительные направления
внутренних сил
![]() (см. рис.3). Силы
(см. рис.3). Силы
![]() и
и
![]() разложим на составляющие по осям
разложим на составляющие по осям
![]() и
и
![]() .
В полученных прямоугольных треугольниках
найдем углы
.
В полученных прямоугольных треугольниках
найдем углы
![]() .
Теперь можно записать аналитические
выражения для внутренних
.
Теперь можно записать аналитические
выражения для внутренних
![]() в функции от текущей координаты
в функции от текущей координаты
![]() ,
используя зависимости (1). Брус имеет
один участок
,
используя зависимости (1). Брус имеет
один участок
![]() .
Из разложений
.
Из разложений
![]() и
и
![]() на прямоугольные треугольники легко
найти:
на прямоугольные треугольники легко
найти:
![]()
![]() ;
;
![]() .
.
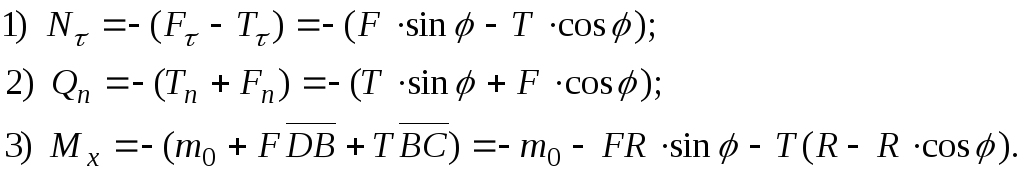 (5)
(5)
Моменты определяются
от сил
![]() и
и
![]() относительно оси х,
проходящей через т. D.
Для силы
относительно оси х,
проходящей через т. D.
Для силы
![]() плечо
плечо
![]() определяется из треугольника ODB
определяется из треугольника ODB
![]() ,
для силы
,
для силы
![]() плечо
плечо
![]() определяется так:
определяется так:
![]() (
(![]() из треугольника OBD).
из треугольника OBD).
В каждом сечении
величины
![]() и
и
![]() откладываем вдоль радиусов, положительные
величины к центру арки, отрицательные
– «наружу».
откладываем вдоль радиусов, положительные
величины к центру арки, отрицательные
– «наружу».
При
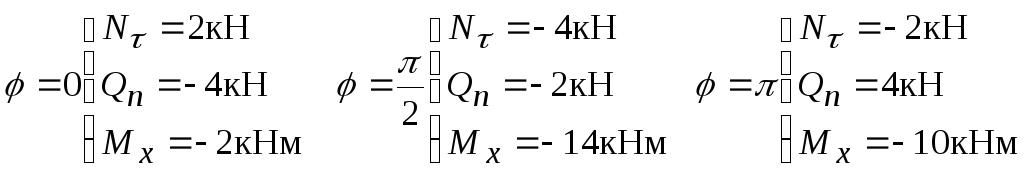
Выберем масштабы
для
![]() и по полученным значениям на эпюрах
строим три точки. На каждой эпюре
соединяем полученные точки, предварительно,
плавными кривыми. Видно, что на участке
и по полученным значениям на эпюрах
строим три точки. На каждой эпюре
соединяем полученные точки, предварительно,
плавными кривыми. Видно, что на участке
![]() эпюра
эпюра
![]() меняет знак, а на участке
меняет знак, а на участке
![]() меняет знак эпюра
меняет знак эпюра
![]() .
.
Обозначим
![]() ,
при котором
,
при котором
![]() ,
т.е. по формуле 1) из (5)
,
т.е. по формуле 1) из (5)
![]() ,
,
откуда
![]() и
и
![]() .
.
Обозначим
![]() ,
при котором
,
при котором
![]() ,
т.е. по формуле 2) из (5)
,
т.е. по формуле 2) из (5)
![]() ,
,
откуда
![]() и
и
![]() .
.
Из дифференциальных соотношений (4) для криволинейного бруса следует:
а)
![]() ,
т.е. в сечении бруса, где
,
т.е. в сечении бруса, где
![]() величина
величина
![]() будет экстремальна. Это при
будет экстремальна. Это при
![]() ;
;
б)
![]() ,
т.е. в сечении бруса, где
,
т.е. в сечении бруса, где
![]() величина
величина
![]() будет экстремальна. Это при
будет экстремальна. Это при
![]() ;
;
в)
![]() ,
т.е. в сечении бруса, где
,
т.е. в сечении бруса, где
![]() величина
величина
![]() будет экстремальна. Это при
будет экстремальна. Это при
![]() .
.
Найдем экстремальные
значения
![]() и
и
![]() по формулам (5)
по формулам (5)
при
![]()
![]() кН;
кН;
при
![]()

На эпюрах внутренних сил строим особые точки. Теперь можно окончательно соединить на каждой эпюре полученные точки плавной кривой. На эпюрах ставятся знаки, штриховка делается по радиусам, указываются особые точки на эпюрах.
Пример №5.
Балка с переменной нагрузкой
![]() (рис. 4)
(рис. 4)
Дано: ![]() 2кН/м,
2кН/м,
![]() 2кН,
2кН,
![]() м,
м,
![]() м,
м,
![]() м
м
Опора А
– шарнирно-неподвижная. Обозначим
![]() –вверх,
–вверх,
![]() вправо. Опора В
– шарнирно-подвижная, обозначим
вправо. Опора В
– шарнирно-подвижная, обозначим
![]() – вверх.
– вверх.
Определение опорных реакций:
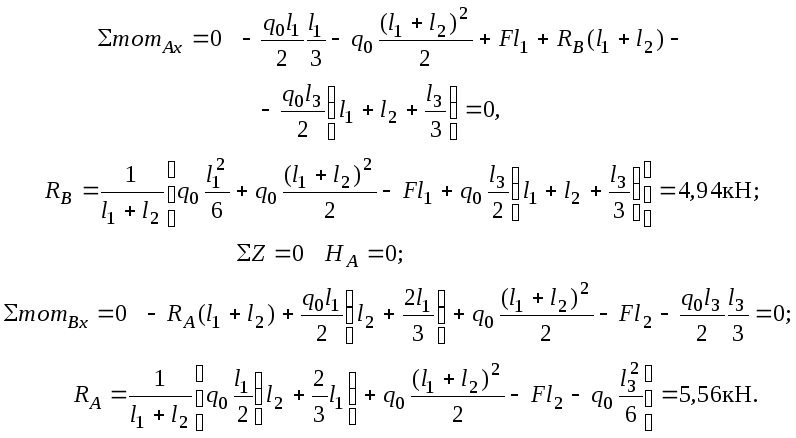
Проверка:
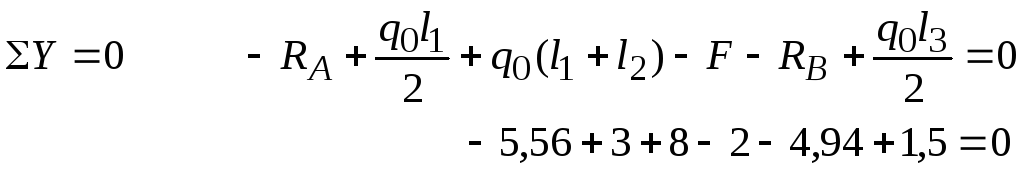
Итак:
![]() кН,
кН,
![]() кН,
кН,
![]() .
Направления опорных реакций, указанных
выше, являются действительными.
.
Направления опорных реакций, указанных
выше, являются действительными.
По характеру конструкции и нагрузки балку делим на три участка.
I
участок
![]() (левая отсеченная часть). Погонную
нагрузку на этом участке представим в
виде суммы прямоугольной и треугольной
нагрузок. Найдем величину этой нагрузки
в сечении с координатой
(левая отсеченная часть). Погонную
нагрузку на этом участке представим в
виде суммы прямоугольной и треугольной
нагрузок. Найдем величину этой нагрузки
в сечении с координатой
![]() ,
для чего предварительно найдем
,
для чего предварительно найдем
![]() для треугольной части нагрузки:
для треугольной части нагрузки:
![]()
![]() .
А для всей нагрузки в сечении с координатой
.
А для всей нагрузки в сечении с координатой
![]() получим
получим
![]() . (В)
. (В)
Используя формулы
для определения внутренних силовых
факторов от погонной нагрузки
![]() и формулы (1), запишем аналитические
зависимости для
и формулы (1), запишем аналитические
зависимости для
![]() и
и
![]() в сечении
в сечении
![]() :
:
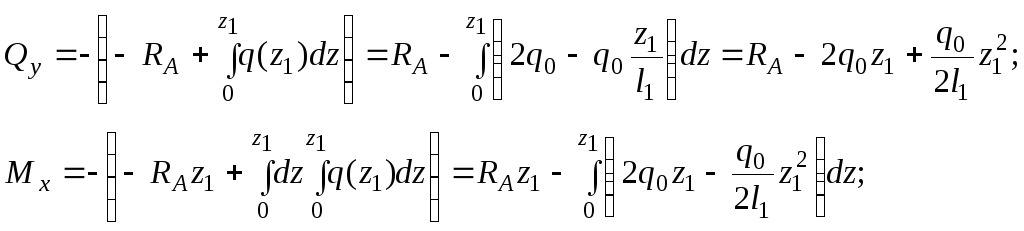
![]() кубическая
зависимость.
кубическая
зависимость.
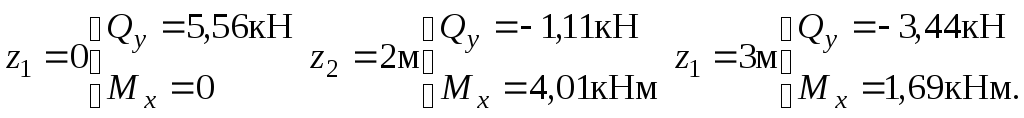
Эпюра
![]() меняет знак. Найдем
меняет знак. Найдем
![]() ,
где
,
где
![]()
![]() .
.
![]() .
.
Решая это квадратное
уравнение, найдем два значения:
![]() м,
м,
![]() м.
Так как
м.
Так как
![]() м,
то на данном участке
м,
то на данном участке
![]() при
при
![]() м.
При
м.
При
![]() м
м
![]() кНм.
кНм.
По полученным
значениям строим эпюры
![]() и
и
![]() на участке.
на участке.
II
участок:
![]() правая отсеченная часть.
правая отсеченная часть.

 Строим
по этим данным эпюры на II
участке.
Строим
по этим данным эпюры на II
участке.
III
участок
![]() правая отсеченная часть.
правая отсеченная часть.
Найдем зависимость
нагрузки
![]() от координаты
от координаты
![]() .
Из подобия треугольников следует
соотношение:
.
Из подобия треугольников следует
соотношение:
![]() ,
откуда
,
откуда
![]() .
По аналогии с I
участком получим
.
По аналогии с I
участком получим
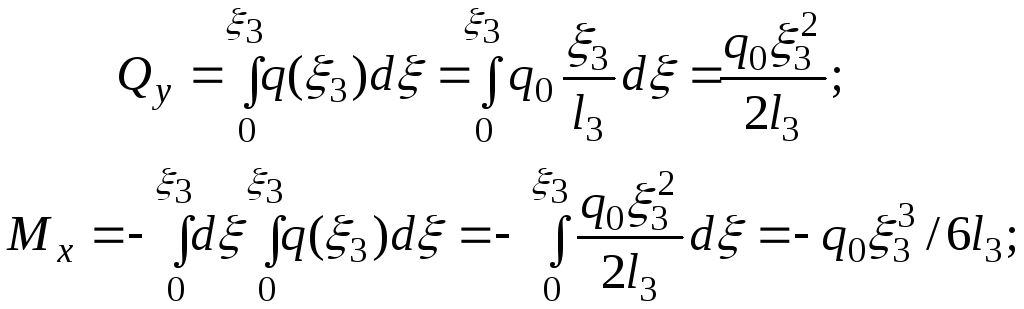

По этим данным
строим эпюры
![]() и
и
![]() на III
участке.
на III
участке.
Пример №6. Сложная рамная конструкция (рис. 5)
Дано: ![]() 1м,
1м,
![]() кН/м,
кН/м,
![]() 2кН,
2кН,
![]() .
.
Величины углов
![]() и
и
![]() не заданы, найдем их. Из рис.5 видно:
не заданы, найдем их. Из рис.5 видно:
![]() т.к.
т.к.
![]() ,
то
,
то
![]() .
.
Опора А
– шарнирно-неподвижная. Обозначим
![]() –вверх,
–вверх,
![]() влево. Опора В
– шарнирно-подвижная, обозначим
влево. Опора В
– шарнирно-подвижная, обозначим
![]() – вверх.
– вверх.
Определение опорных реакций
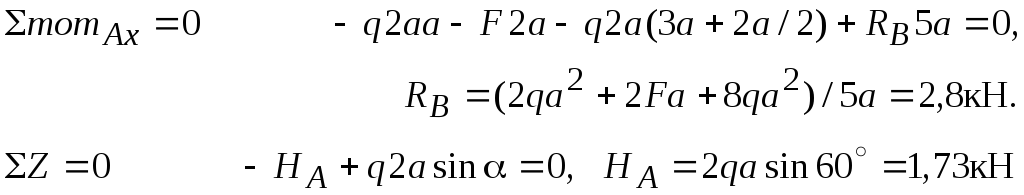
Теперь можно рассмотреть и уравнение равновесия
![]() .
.
Отрезок
![]() найдем из построений на рис. 5:
найдем из построений на рис. 5:
![]()
![]() .
.
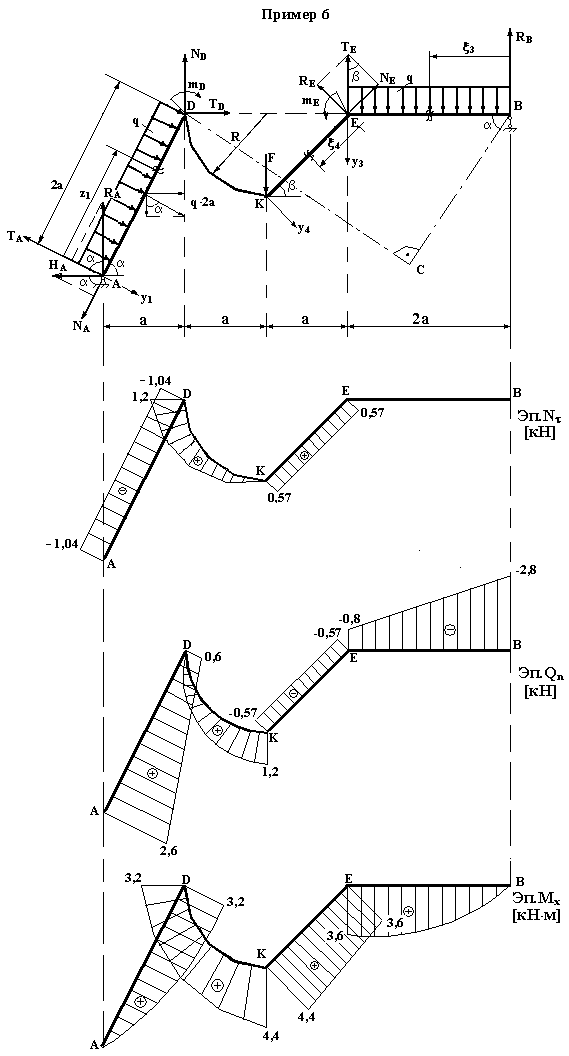
Рис.5
Проверка:
![]() .
.
Итак:
![]() кН,
кН,
![]() кН,
кН,
![]() кН.
кН.
Указанные выше их направления являются действительными.
По характеру
конструкции и нагрузки можно выделить
четыре участка:
![]() криволинейный,
криволинейный,
![]() и
и
![]() .
Для каждого участка будем вводить свою
систему координат
.
Для каждого участка будем вводить свою
систему координат
![]() (как в примере №3).
(как в примере №3).
I
участок
![]() (наклонный). Ось
(наклонный). Ось
![]() направим от т.А
к т.
направим от т.А
к т.
![]() ,
оси
,
оси
![]() и
и
![]() составляют с осью
составляют с осью
![]() правую систему координат. Проведем
поперченное сечение. Видно, что проще
рассматривать левую часть от сечения,
т.е.
правую систему координат. Проведем
поперченное сечение. Видно, что проще
рассматривать левую часть от сечения,
т.е.
![]() (левая отсеченная часть). Для удобства
построения эпюр реакции
(левая отсеченная часть). Для удобства
построения эпюр реакции
![]() и
и
![]() удобно заменить реакциями
удобно заменить реакциями
![]() и
и
![]() ,
которые определяются так:
,
которые определяются так:
![]()
т.е. реакция
![]() в действительности противоположна
нарисованной на рис. 5.
в действительности противоположна
нарисованной на рис. 5.
Итак:
![]() = 2,6кН,
= 2,6кН,
![]() = –1,04кН. Для записи аналитических
выражений для
= –1,04кН. Для записи аналитических
выражений для
![]() и
и
![]() используем формулы (1):
используем формулы (1):
![]()
при
 при
при
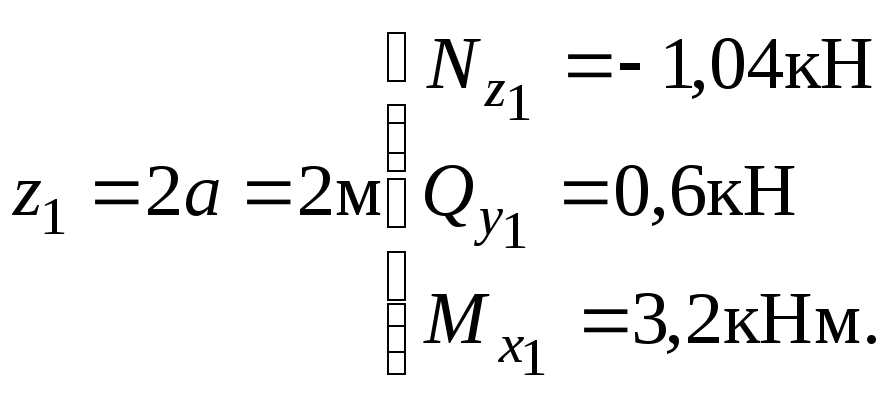
Откладываем
полученные значения в масштабе
перпендикулярно оси стержня и строим
эпюры на этом участке. Для
![]() надо еще третью точку при
надо еще третью точку при
![]() .
.
II
участок
![]() (криволинейный, радиуса
(криволинейный, радиуса
![]() ).
Проведем поперечное сечение в произвольной
т.
).
Проведем поперечное сечение в произвольной
т.![]() .
Внутренние усилия в этом сечении найдем,
рассматривая участок
.
Внутренние усилия в этом сечении найдем,
рассматривая участок
![]() .
Для удобства перенесем нагрузки,
действующие на участке
.
Для удобства перенесем нагрузки,
действующие на участке
![]() ,
в т.
,
в т.
![]() .
При этом в т.
.
При этом в т.
![]() возникнут:
возникнут:
![]()
В сечении
![]() введем систему координат
введем систему координат
![]() так, чтобы ось
так, чтобы ось
![]() была направлена по касательной в т.
была направлена по касательной в т.![]() и направлена наружу от рассматриваемой
части
и направлена наружу от рассматриваемой
части
![]() .
Положение т.
.
Положение т.
![]() будем определять
будем определять
|
|
текущей координатой
|
при
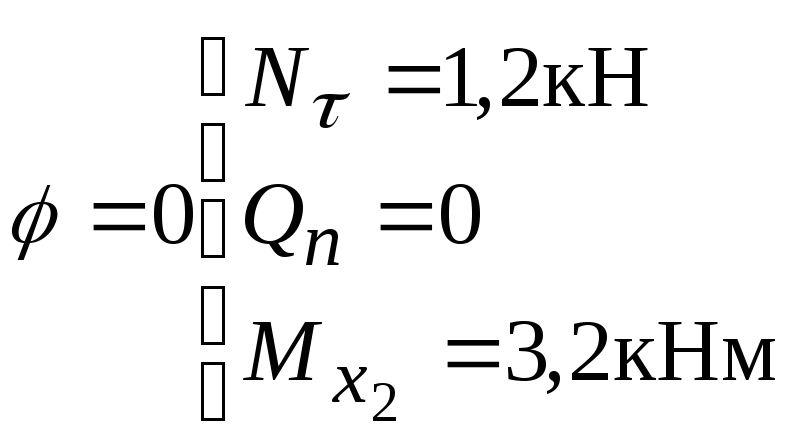 ;
при
;
при
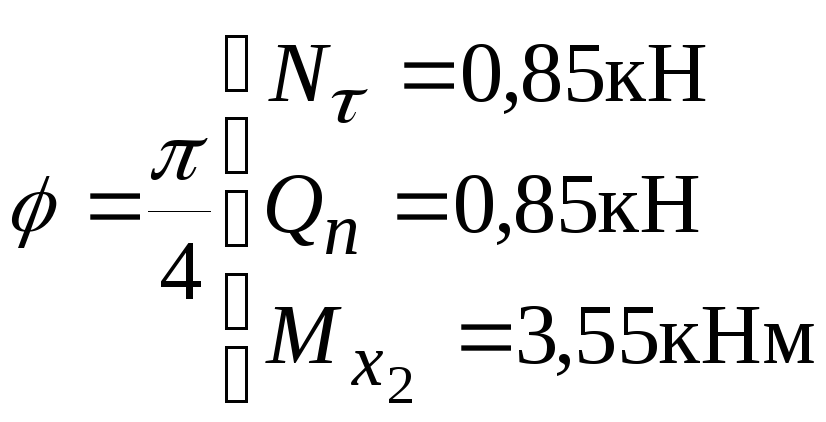 ;
;
при

Полученные значения
откладываем вдоль радиусов и строим
эпюры
![]() и
и
![]() на этом участке.
на этом участке.
III
участок
![]() .
Проведем поперечное сечение, видно, что
проще рассмотреть правую отсеченную
часть, т.е.
.
Проведем поперечное сечение, видно, что
проще рассмотреть правую отсеченную
часть, т.е.
![]() .
Используя формулы (2), получим:
.
Используя формулы (2), получим:
![]()
при
 при
при
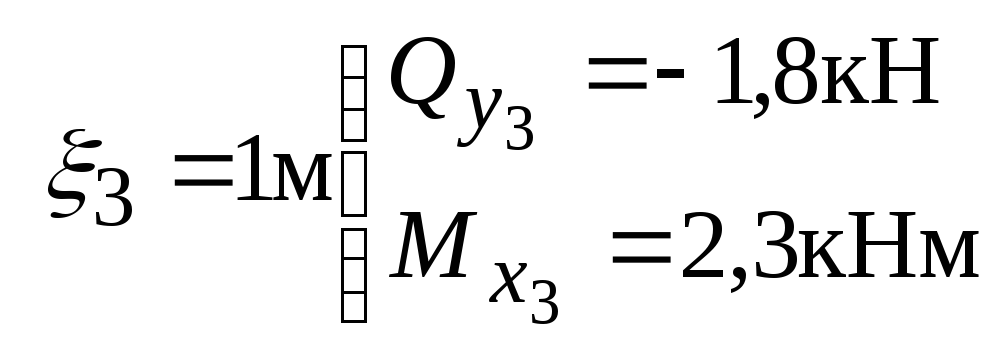 ;
;
при
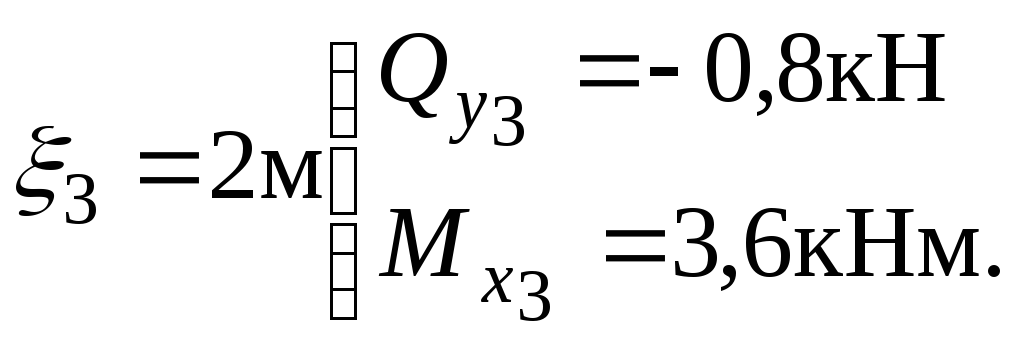
Строим эпюры
![]() и
и
![]() на этом участке.
на этом участке.
IV
участок
![]() (наклонный). Ось
(наклонный). Ось
![]() ,
направим от т.
,
направим от т.
![]() к т.
к т.
![]() .
Проведем поперечное сечение. Видно, что
проще рассмотреть правую отсеченную
часть. Перенесем нагрузки с участка
.
Проведем поперечное сечение. Видно, что
проще рассмотреть правую отсеченную
часть. Перенесем нагрузки с участка
![]() в т.
в т.
![]() ,
при этом в т.
,
при этом в т.
![]() возникнут:
возникнут:
![]() .
.
Силу
![]() разложим на составляющие по осям
разложим на составляющие по осям
![]() и
и
![]() :
:
![]() .
.
Длина стержня
![]() равна:
равна:
![]() .
.
Следовательно,
![]() .
.
Используя формулы (2), найдем внутренние усилия на торце правой отсеченной части:
![]()
при
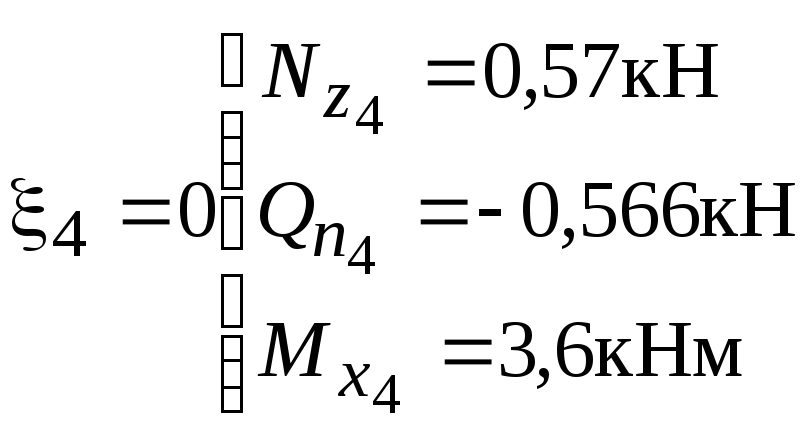 ;
при
;
при
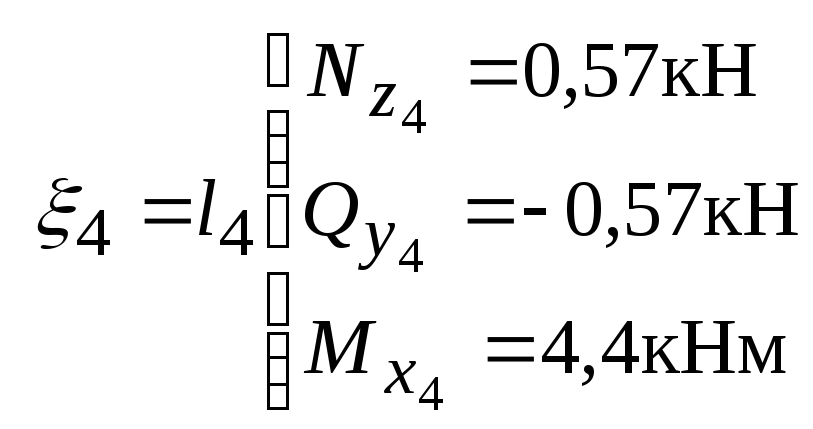
Полученные значения
откладываем в выбранном масштабе
перпендикулярно оси
![]() и строим эпюры
и строим эпюры
![]() .
.
На эпюрах ставим знаки и делаем штриховку.
Литература
1. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности. – М.: Высшая школа, 1984. – С. 31-51.
Построение эпюр внутренних силовых
факторов при плоском изгибе балки
Методические указания по выполнению расчетно-графической работы
для студентов специальностей 1203, 1205, 1207, 1208, 1210, 1211
Составитель: МАРТЫШЕВ Вячеслав Петрович
Редактор
Корректор
Подписано в печать Бесплатно Формат 60х84/16,
Бумага тип.№ 2, Печать офсетная Усл.печ.л.1,0
Заказ Тираж 300 экз Уч.-изд.л.1,0
![]()

Адрес университета и офсетной лаборатории:

