
- •Дифференциальное исчисление функции двух и более переменных Частные производные , их геометрический и физический смыслы
- •Понятие дифференцируемости функции . Полный дифференциал .
- •Сложная функция двух переменных и ее дифференцирование
- •Инвариантность формы полного дифференциала сложной функции двух переменных
- •О частных производных и дифференциалах высших порядков.
- •О неявном способе задания функции двух переменных и ее дифференцировании в этом случае
- •Уравнение касательной плоскости и нормали к поверхности (в )
- •О геометрической интерпретации
- •О формуле Тейлора для функции двух переменных
- •Экстремум функции двух переменных
- •Необходимые условия существования экстремума
- •Достаточные условия существования экстремума в точке функции
- •Нахождение наибольшего и наименьшего значений в замкнутой области
- •Об условном экстремуме. Функция и множитель Лагранжа (для )
О геометрической интерпретации
Е сли
сли
![]() ,
где
,
где ![]() - касательная плоскость, то точка
- касательная плоскость, то точка ![]() имеет координаты
имеет координаты
![]() .
Подставим координаты точки
.
Подставим координаты точки ![]() в уравнение (8):
в уравнение (8):
![]()
Итак,
![]() - приращение аппликаты точки касательной
плоскости. Из рисунка следует, что
- приращение аппликаты точки касательной
плоскости. Из рисунка следует, что
![]() и
и ![]() (у нас на чертеже).
(у нас на чертеже).
О формуле Тейлора для функции двух переменных
Пусть
![]() (
(![]() непрерывные частные производные в
некоторой области
непрерывные частные производные в
некоторой области ![]() , содержащей точку
, содержащей точку ![]() ,
до
,
до ![]() порядка включительно).
порядка включительно).
Пусть
![]() и
и ![]() такие, что
такие, что

![]() .
.
[
![]() такое число
такое число ![]() ,
что имеет место формула Тейлора n-ого
порядка
,
что имеет место формула Тейлора n-ого
порядка
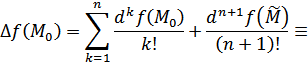
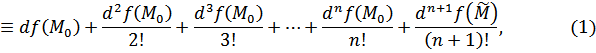
где
![]()
1)
] в (1) ![]() .
Тогда
.
Тогда

(2) - формула Тейлора первого порядка, причем
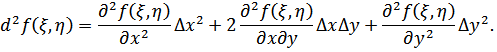
2)
]
в
(1) ![]() :
:
![]()
- формула Тейлора третьего порядка,

Идея доказательства формулы (1):
1)
уравнение ![]() :
:
![]()
![]()
![]()
2)
![]()
3)
![]()
![]()
4)
![]()
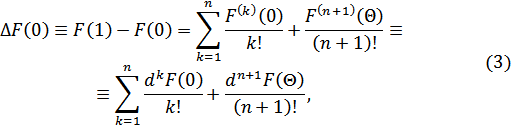
![]()
5) у нас
![]()
![]()
6) Получаем формулу (1), если подставить (4) и (5) в (3).
Экстремум функции двух переменных
П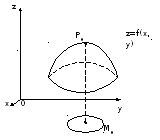 усть
усть
![]() в некоторой области
в некоторой области ![]()
def 1.
![]() если
если
![]() ,
что
,
что
![]()
![]()
или
![]()
def
2.
![]() ,
если
,
если ![]() ,
что
,
что
![]()
![]()
![]()
или
![]()
В
(1) и (2) говорят о строгом ![]() или
или ![]() ( в случае ≤ или ≥ слово
( в случае ≤ или ≥ слово ![]() опускают).
опускают).
def
3.
Точки ![]() и точки
и точки ![]() - точки экстремума функции
- точки экстремума функции ![]() .
.
![]()
![]() сохраняет
знак в
сохраняет
знак в
![]() :
:![]() в
в
![]() ).
).
Необходимые условия существования экстремума
Теорема.
]
1) ![]() ( в точке
( в точке ![]() и ее окрестности ), то есть
и ее окрестности ), то есть ![]() ,
,
2)
![]() ,
,
3)
![]() .
.
[
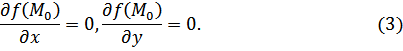
Доказательство.
Фиксируем ![]() ,
то есть ]
,
то есть ] ![]() для
для ![]() ,
рассмотрим
,
рассмотрим ![]() - функцию одной переменной
- функцию одной переменной ![]() . Точка
. Точка ![]() - точка экстремума для
- точка экстремума для ![]() .
По теореме Ферма (так как
.
По теореме Ферма (так как ![]()
![]() .
.
Аналогично
доказывается, что ![]() (фиксируя
(фиксируя ![]() ).
).
Следствие.
Если 1) ![]() ,
2)
,
2) ![]() ,
то
,
то ![]() .
Из условий 1) – 3) теоремы и
.
Из условий 1) – 3) теоремы и ![]() →
→![]() и в силу (3) они равны нулю. [
и в силу (3) они равны нулю. [![]() .
.
Замечание:
аналогичные необходимые условия имеют
место и для ![]()
Пример
1.
Исследовать на экстремум ![]() .
.
Решение.
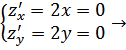 в точке
в точке ![]() .
В
.
В ![]()
Таким
образом, точка ![]() .
.
Пример
2.
Исследовать на экстремум ![]() .
.

![]() - стационарная точка →
- стационарная точка →![]() .
.
![]() -
приращение
меняет знак в окрестности
-
приращение
меняет знак в окрестности ![]() .
Следовательно,
.
Следовательно, ![]() вообще не имеет экстремальных точек.
Это подчеркивает, что условия
вообще не имеет экстремальных точек.
Это подчеркивает, что условия 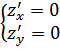 необходимые, но недостаточные.
необходимые, но недостаточные.
def
4.
Пусть ![]() .
Если
.
Если
![]()
то
точка ![]() - стационарная точка функции
- стационарная точка функции ![]() (или точка
(или точка ![]() ).
).
Достаточные условия существования экстремума в точке функции
Введем обозначения:
![]()
и пусть
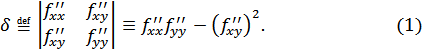
Теорема.
Пусть
1) ![]() и
и ![]() (имеет непрерывные частные производные
до второго порядка включительно).
(имеет непрерывные частные производные
до второго порядка включительно).
2)
точка ![]() - стационарная точка(
- стационарная точка(![]() )
)
Тогда
а) ] ![]() ,
то
,
то ![]() ,
,
причем
1) при ![]() – точка
– точка![]() ,
,
2) при ![]() - точка
- точка![]()
Замечание:
![]() ,
ибо ]
,
ибо ] ![]() ,
[
,
[![]() .
.
]
![]() ,
то экстремума в точке
,
то экстремума в точке ![]() нет и
нет и ![]() .
.
]
![]() ,
экстремум в точке
,
экстремум в точке ![]() может быть, а может и не быть, требуется
дополнительное исследование.
может быть, а может и не быть, требуется
дополнительное исследование.
Доказательство. Напишем формулу Тейлора второго порядка:
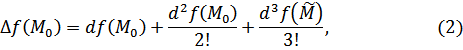
где
![]()
Так
как точка ![]() - стационарная точка, то
- стационарная точка, то
![]() и (2) примет вид:
и (2) примет вид:
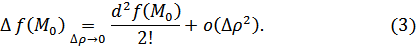
Показывается,
что слагаемое ![]() не влияет на знак
не влияет на знак ![]() и, следовательно,
и, следовательно,
![]()
где

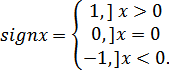
Исследуем
![]() .
.
Имеем:
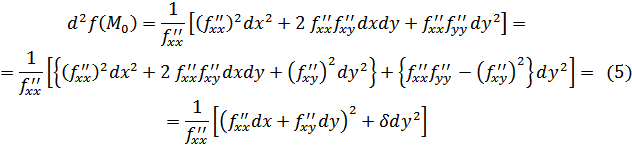
а)
Пусть в (5) ![]() .
[ из (5) следует, что
.
[ из (5) следует, что
![]()
Из (4)и (6)следует
![]()
Равенство (7) позволяет утверждать:
1)![]() ,
[
,
[![]() в
в ![]() и
и ![]() ,
,
2)
![]() ,
[
,
[![]() в
в ![]() и
и ![]() .
.
б)
Пусть в (5) ![]() .
.
Выберем
1) ![]() ,
[
,
[
![]()
2)
] ![]() ,
а
,
а ![]() .
[
.
[
![]()
Из
(8), (9) с учетом (4) следует вывод: ![]() меняет знак в
меняет знак в ![]() .
Следовательно, в
.
Следовательно, в ![]() экстремума нет.
экстремума нет.
![]()
в)
Пусть в (5) ![]() .
Любопытно, что в этом случае экстремум
может быть, а может и не быть, требуется
дополнительное исследование.
.
Любопытно, что в этом случае экстремум
может быть, а может и не быть, требуется
дополнительное исследование.
Рассмотрим этот случай на примерах (что достаточно для доказательства).
1)
] ![]() .
Имеем:
.
Имеем:
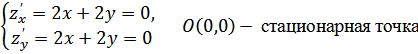 ,
,
ибо
![]() .
Далее
.
Далее
![]()
С другой стороны,
![]()
![]() и
и ![]() .
.
2)
] ![]() .
.
Далее
![]() .
.
Но
![]() меняет
знак в
меняет
знак в ![]() . Это означает, что точка
. Это означает, что точка ![]() не является точкой экстремума функции
не является точкой экстремума функции
![]() .
.
Итак,
из рассмотренных примеров следует, что
в случае![]() экстремум может быть, а может и не быть.
экстремум может быть, а может и не быть.
