
- •Дифференциальное исчисление функции двух и более переменных Частные производные , их геометрический и физический смыслы
- •Понятие дифференцируемости функции . Полный дифференциал .
- •Сложная функция двух переменных и ее дифференцирование
- •Инвариантность формы полного дифференциала сложной функции двух переменных
- •О частных производных и дифференциалах высших порядков.
- •О неявном способе задания функции двух переменных и ее дифференцировании в этом случае
- •Уравнение касательной плоскости и нормали к поверхности (в )
- •О геометрической интерпретации
- •О формуле Тейлора для функции двух переменных
- •Экстремум функции двух переменных
- •Необходимые условия существования экстремума
- •Достаточные условия существования экстремума в точке функции
- •Нахождение наибольшего и наименьшего значений в замкнутой области
- •Об условном экстремуме. Функция и множитель Лагранжа (для )
Дифференциальное исчисление функции двух и более переменных Частные производные , их геометрический и физический смыслы
def 1.
![]()
называется
производной от ![]() по
по![]() при фиксированном
при фиксированном ![]() или частной производной от
или частной производной от ![]() по
по![]() .
.
def 2.
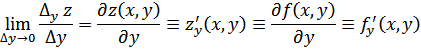
называется
производной от ![]() по
по![]() при фиксированном
при фиксированном ![]() или частной производной от
или частной производной от ![]() по
по![]() .
.
Из
введенных определений следует, что
нахождение ![]() и
и ![]() сводится к обычному дифференцированию
соответственно по
сводится к обычному дифференцированию
соответственно по ![]() (при
(при ![]() )
и по
)
и по ![]() (при
(при ![]() )
и использованию таблицы производных
функции одной переменной.
)
и использованию таблицы производных
функции одной переменной.
Пример.
![]() .
.
![]()
![]() .
.
а )
геометрический смысл
)
геометрический смысл ![]() и
и ![]() .
.
Из рисунка 1 →
![]()
г
Рис.
1![]() - угол наклона касательной
- угол наклона касательной ![]() к кривой
к кривой ![]() в точке
в точке ![]() .
.
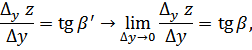 где
где
![]() - угол наклона касательной
- угол наклона касательной ![]() к линии
к линии![]() в точке
в точке ![]() .
.
б)
] ![]() - температура стержня, как функция данной
точки
- температура стержня, как функция данной
точки ![]() стержня и от времени
стержня и от времени ![]() .
.
Ay
xy xy
0y


![]() -
скорость изменения температуры стержня
в каждой точке стержня при фиксированном
моменте времени
-
скорость изменения температуры стержня
в каждой точке стержня при фиксированном
моменте времени ![]()
![]() -
скорость изменения температуры стержня
в фиксированной точке стержня в каждый
момент времени
-
скорость изменения температуры стержня
в фиксированной точке стержня в каждый
момент времени ![]() .
.
Понятие дифференцируемости функции . Полный дифференциал .
def.
Функция ![]() называется дифференцируемой в точке
называется дифференцируемой в точке![]() ,
если
,
если
![]()
где
![]() и
и ![]() числа, не зависящие от
числа, не зависящие от ![]() и
и ![]() ,
а
,
а ![]() и
и ![]() →0
при
→0
при ![]() и
и ![]() →0
(
→0
(![]() .
.
В этом случае будем писать
![]()
Итак, (1) ~ (2).
Теорема 1 .
Если
![]() ,
то
,
то ![]() .
Доказательство следует из (1):
.
Доказательство следует из (1):
![]()
Теорема 2.
Если
![]() ,
то
,
то ![]() в точке
в точке ![]() и
и ![]() ,
причем
,
причем ![]() и
и ![]() ,
,
![]() .
.
Доказательство.
Пусть
![]() и
и ![]()
![]() при
при ![]() и
и ![]() (то есть
(то есть ![]() ).
).
Положим
в (1) ![]() :
:
![]()
Аналогично,
при ![]() из (1):
из (1):

Из
теоремы 2 следует, что если ![]() ,
[
,
[
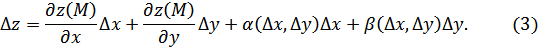
def.
Выражение вида
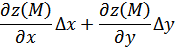
называют
полным дифференциалом ![]() в точке
в точке ![]() и пишут
и пишут
![]()
Замечание.
Утверждения, обратные теоремам 1 и 2, не имеют место в общем случае.
Пример.
]
![]() (часть конической поверхности
(часть конической поверхности ![]() ).
).
Так
как ![]() при
при ![]() и
и ![]() →0,
то
→0,
то ![]()
Однако
![]() и
и ![]() и предела не
и предела не ![]() .
Что и означает
.
Что и означает ![]() ,
ибо не имеет место равенство (1); то есть
из
,
ибо не имеет место равенство (1); то есть
из ![]()
Пример.
]
![]() .
.
Имеем:
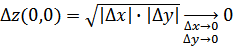 и
и ![]() .
.
далее:
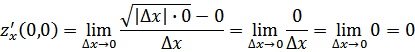
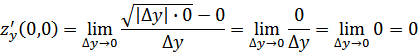
то
есть ![]() и
и ![]() функции
функции ![]()
![]() в точке
в точке ![]() и равны 0.
и равны 0.
В силу (1)

Но
![]() .
.
С другой стороны:
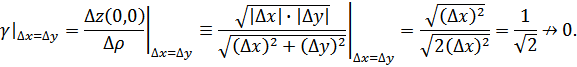
(![]()
Полученное
противоречие ![]() показывает, что
показывает, что ![]() ,
хотя
,
хотя ![]() и
и ![]() .
Вместе с тем имеет место
.
Вместе с тем имеет место
Теорема
3
(достаточное условие дифференцируемости![]() или
или ![]() ).
).
]
1) ![]()
![]() и
и ![]() для всех точек
для всех точек ![]() .
.
2)
![]() и
и ![]() .
.
[
![]() .
.
Краткое
обоснование. ] ![]()
![]()
![]()
![]() ,
,
где
![]() .
.
В
силу непрерывности ![]() и
и ![]()
![]() :
:
![]() [
[
![]()
где
![]() ,
а
,
а
![]()
![]() и
и ![]() →0
при
→0
при ![]() .
.
Из
(5) и следует, что ![]() (определение 1) теорема 3 доказана.
(определение 1) теорема 3 доказана.
Важное замечание.
В
отличие от функции одной переменной,
(где ![]() )
для
)
для ![]() мы имеем лишь достаточное условие
дифференцируемости
мы имеем лишь достаточное условие
дифференцируемости ![]() .
.
С учетом (4), (5) перепишем:
![]()
В равенстве (6)
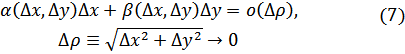
В
силу (7) ![]() :
:
![]()
Из
(8) ![]()
![]()
(ибо
![]() и
и
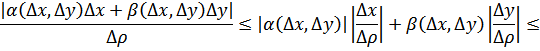
![]()
Соотношение (9) удобно использовать в приближенных вычислениях.
Пример.
Вычислить
![]() при
при ![]()
Решение:
![]()
]
![]()
[ в силу (9)
![]()
![]()
Итак,
![]() .
.
Напишем (9) в «развернутом» виде
![]()
Именно в этом виде мы и использовали формулу (9).
Сложная функция двух переменных и ее дифференцирование
а) def
]
![]()
а
![]()
Функцию (1), (2) называют сложной функцией (независимой переменной t); x и y – промежуточнаые переменные, зависящие от одной и той же переменной t.
Подставим (2) в (1):
![]()
получили функцию одной переменной z= z(t).
Теорема.
]
1) ![]()
2)
![]()
![]() и
и
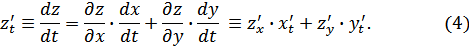
def: (4) – «полная» производная функция (1),(2).
Доказательство.
Дадим ![]() приращение
приращение ![]() .
[
.
[![]()
![]() и
и ![]() .
.
По
условию 2) ![]() .
Это означает, что
.
Это означает, что
![]()
Разделим
(5) на ![]() и перейдем к пределу при
и перейдем к пределу при ![]() (при этом
(при этом ![]() и
и ![]() )
)
![]()
![]() - теорема доказана.
- теорема доказана.
Замечание.
]
![]() и
и ![]() .
[
.
[![]() и
и ![]()
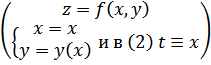 ,
причем
,
причем ![]() .
.
Пусть в (1)
![]()
Причем
![]() ,
где
,
где ![]()
б) def
Функция
![]()
![]()
называется
сложной функцией двух переменных: ![]() и
и ![]() -
промежуточные переменные, а
-
промежуточные переменные, а ![]() и
и ![]() –
независимые переменные.
–
независимые переменные.
Теорема.
]
1) ![]() и
и ![]()
2)
![]()
[
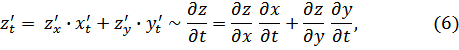
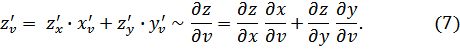
Для
доказательства (6) фиксируем![]() в
(1), (5). Повторяя рассуждения при
доказательстве формулы (4), приходим к
формуле (6). Формула (7) получится, если
фиксировать
в
(1), (5). Повторяя рассуждения при
доказательстве формулы (4), приходим к
формуле (6). Формула (7) получится, если
фиксировать ![]() в (1) и (5).
в (1) и (5).
в) Пусть
![]()

и
![]()
![]()
г) Если
![]()
то
![]()
![]()
Формула (10) – «полная» производная для (9), (8).
Формула (8а) – «полная» производная для (7а), (8).
Замечание:
Выражение
![]() производная синоним обычной производной
(производной функции одной переменой),
причем для (10)
производная синоним обычной производной
(производной функции одной переменой),
причем для (10)
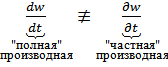 (по смыслу).
(по смыслу).
