
- •Дифференциальное исчисление функции двух и более переменных Частные производные , их геометрический и физический смыслы
- •Понятие дифференцируемости функции . Полный дифференциал .
- •Сложная функция двух переменных и ее дифференцирование
- •Инвариантность формы полного дифференциала сложной функции двух переменных
- •О частных производных и дифференциалах высших порядков.
- •О неявном способе задания функции двух переменных и ее дифференцировании в этом случае
- •Уравнение касательной плоскости и нормали к поверхности (в )
- •О геометрической интерпретации
- •О формуле Тейлора для функции двух переменных
- •Экстремум функции двух переменных
- •Необходимые условия существования экстремума
- •Достаточные условия существования экстремума в точке функции
- •Нахождение наибольшего и наименьшего значений в замкнутой области
- •Об условном экстремуме. Функция и множитель Лагранжа (для )
Инвариантность формы полного дифференциала сложной функции двух переменных
Пусть
![]()
![]()
![]()
причем
![]()
![]()
Подставим
(2) в (1)→: ![]() причем
причем ![]() и
и ![]()
![]() и
и
![]()
или
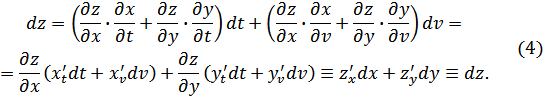
Из (3) и (4) следует, что форма полного дифференциала для (1) и (2) неизменна.
Замечание.
Из (4) получим (3), двигаясь в обратном порядке.
О частных производных и дифференциалах высших порядков.
1) Пусть
![]() и
и ![]()
![]() и
и ![]() .
(1)
.
(1)
Если
![]() и
и ![]() дифференцируемы в некоторой точке
дифференцируемы в некоторой точке ![]() ,
то
,
то ![]() и
и ![]() ,
,
![]() Что обозначают так:
Что обозначают так:
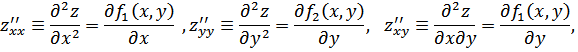
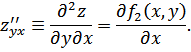
Теорема.
]1)![]() ,
2)
,
2) ![]()
![]()
Аналогично
определяются частные производные
третьего, четвертого и так далее ![]() -ого
порядка
-ого
порядка
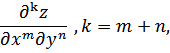
где
![]() - общее число дифференцирований
- общее число дифференцирований ![]() ,
,
![]() -
число дифференцирований по
-
число дифференцирований по ![]() ,
,
![]() - число дифференцирований по
- число дифференцирований по ![]() .
.
Например,
![]() и т.д.
и т.д.
Пример.
Убедиться, что ![]() ,
если
,
если ![]()
Решение:
![]() ,
,
![]() .
.
2) def:
![]() - дифференциал второго порядка функции
- дифференциал второго порядка функции
![]()
Вообще
![]() – дифференциал -ого порядка
– дифференциал -ого порядка ![]() ,
при условии, ]
,
при условии, ] ![]()
![]() частные производные соответствующих
порядков.
частные производные соответствующих
порядков.
Имеем:
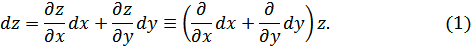
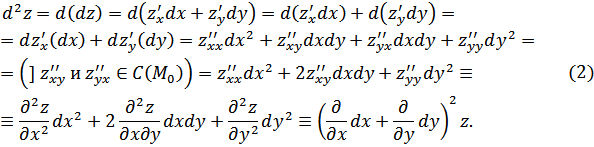
Используя (1) и (2), аналогично получим:
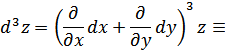
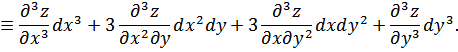
В общем случае
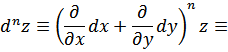
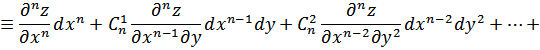
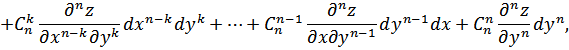
где
![]()
О неявном способе задания функции двух переменных и ее дифференцировании в этом случае
]
![]() def
некоторую функцию
def
некоторую функцию ![]() ,
то есть
,
то есть ![]() .
Например,
.
Например, ![]() def:
def:
![]() .
.
Теорема.
] 1) ![]() ,
где
,
где ![]() - открытый шар с центром в точке
- открытый шар с центром в точке ![]() и радиуса
и радиуса ![]() :
:
![]()
![]()
2)![]()
![]()
3)
![]()
[
в ![]()
![]() определяет
определяет ![]() как однозначную функцию от
как однозначную функцию от ![]() и
и ![]() :
:
![]() так, что
так, что
а)![]()
б)
![]()
в)
![]()
Идея
получения формул (3) из ![]()

Пример.
Пусть ![]() определяется уравнением
определяется уравнением
![]()
Найти:![]() .
.
Решение.]
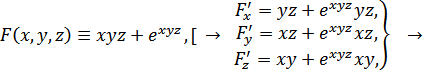
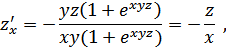

Уравнение касательной плоскости и нормали к поверхности (в )
Пусть
поверхность ![]() (в
(в ![]() )
задана неявно уравнением
)
задана неявно уравнением
![]()
Пусть
![]() .
Проведем через точку
.
Проведем через точку ![]() линию
линию ![]() и заданную параметрически (в
и заданную параметрически (в ![]() ):
):
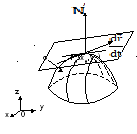
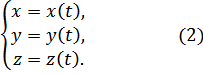
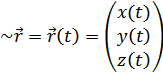 -
-
![]()
Так
как ![]() ,
то (2) обращает (1) в тождество
,
то (2) обращает (1) в тождество
![]()
![]()
Из (3) следует, что
![]()
Пусть
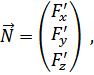

Тогда (4) перепишем

Вектор![]() – вектор, касательный к линии
– вектор, касательный к линии ![]() в точке
в точке ![]() .
Из (6) следует, что он
.
Из (6) следует, что он ![]() .
Через точку
.
Через точку ![]() можно провести множество линий
можно провести множество линий ![]() ,
и для касательных векторов которых
,
и для касательных векторов которых ![]() (6). Отсюда следует, что касательные
прямые к этим линиям лежат в одной
плоскости, которую и называют касательной
плоскостью
(6). Отсюда следует, что касательные
прямые к этим линиям лежат в одной
плоскости, которую и называют касательной
плоскостью![]() (как объединение всех касательных
прямых). Вектор
(как объединение всех касательных
прямых). Вектор ![]() - нормальный вектор касательной плоскости,
а прямая, на которой лежит вектор
- нормальный вектор касательной плоскости,
а прямая, на которой лежит вектор ![]() - нормаль к поверхности
- нормаль к поверхности ![]() в точке
в точке ![]() .
.
Пусть
![]() причем
причем ![]() (то есть
(то есть ![]()
Очевидно,
что уравнение касательной плоскости
имеет вид (в точке ![]() )
)
![]()
ибо
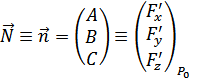 (
(![]() – нормальный вектор касательной
плоскости), а уравнение нормали:
– нормальный вектор касательной
плоскости), а уравнение нормали:
![]()
ибо
![]() (
(![]() - направляющий вектор нормали).
- направляющий вектор нормали).
Пусть
![]()
Это
означает, что поверхность ![]() задана в явном виде:
задана в явном виде:
![]()
![]()
Тогда
из (6в) →![]() и уравнения касательной плоскости и
нормали к поверхности в точке
и уравнения касательной плоскости и
нормали к поверхности в точке ![]() принимают вид:
принимают вид:
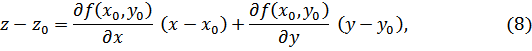
![]()
