
- •Методическое пособие по физике Методы решения базовых задач по механике
- •Содержание
- •Предисловие
- •I. Кинематика материальной точки
- •1. Векторный способ
- •Решение задач
- •2. Координатный способ описания движения
- •Решение задач
- •3. Естественный способ описания движения
- •Решение задач
- •II. Кинематика твёрдого тела
- •1. Вращение твердого тела вокруг неподвижной оси Решение задач
- •2. Плоскопараллельное движение (ппд) твёрдого тела
- •Решение задач
2. Координатный способ описания движения
Само название этого способа описания движения говорит о том, что положение точки характеризуется тремя координатами
![]() ,
, ![]() ,
,
![]() .
.
Зная зависимости этих координат от времени, можно найти положение точки в каждый момент времени, ее скорость и ускорение, то есть решить прямую и обратную задачи кинематики, рассмотренные ранее.
Решение задач
1.5.
Воздушный шар начинает подниматься с
поверхности Земли. Скорость его подъёма
постоянна и равна
![]() 0.
Благодаря ветру шар приобретает
горизонтальную компоненту скорости
0.
Благодаря ветру шар приобретает
горизонтальную компоненту скорости
![]() ,
где
,
где
![]() - постоянная,
y
- высота
подъёма. Найти зависимость от времени:
- постоянная,
y
- высота
подъёма. Найти зависимость от времени:
а) координат шара x(t) и y(t);
б) скорость и ускорение шара;
в) уравнение траектории x(y).
Решение.
а) Из
условия задачи
![]() ,
поэтому
,
поэтому
![]() ,
,
Из
начальных условий
![]() при
t = 0,
следовательно,
при
t = 0,
следовательно,
![]() .
.
Тогда
![]() .
.
По
условию
![]() ,
поэтому
,
поэтому
![]() ,
,
![]() при
t = 0,
следовательно,
при
t = 0,
следовательно,
![]() ,
а
,
а
![]() .
.
б)
Выше были определены выражения для
![]() и
и
![]() .
.
Теперь определим проекции вектора ускорения на оси X и Y
![]() ,
,
![]() .
.
Обозначая
орты осей X
и Y
через
![]() и
и
![]() соответственно, запишем выражения для
векторов скорости и ускорения
соответственно, запишем выражения для
векторов скорости и ускорения
![]() ,
,
![]() .
.
Модули скорости и ускорения соответственно равны
![]()
 ,
,
![]() .
.
г)
Зная зависимости
![]() и
и
![]() (пункт а), исключим из них время
(пункт а), исключим из них время
![]() и получим уравнение траектории шара
и получим уравнение траектории шара
![]() .
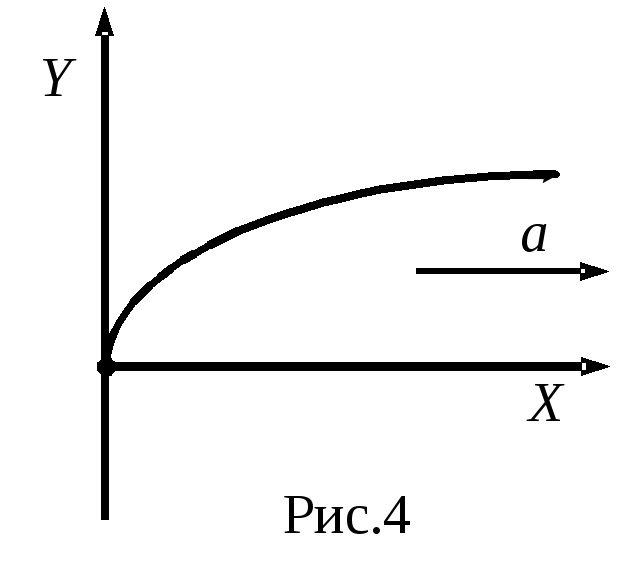
.
График функции x(y) схематично представлен на рис.4.
1.6*.
Точка движется в плоскости XY
по закону
![]() ;
;
![]() ,
где
,
где
![]() и
и
![]() - положительные постоянные. Найти:
- положительные постоянные. Найти:
а) уравнение траектории точки y(x);
б) скорость и ускорение точки, а также их модули в зависимости от t;
в)
момент времени t0,
когда угол между скоростью и ускорением
равен
![]() .
.
Решение. а) По условию
![]() ,
,
![]() .
.
Выразив
из первого уравнения время
![]() и подставив его во второе уравнение,
получим уравнение траектории точки
и подставив его во второе уравнение,
получим уравнение траектории точки
![]() .
.
Полученное уравнение является уравнением параболы, обращённой ветвями вниз, так как коэффициент при x2 меньше нуля. График параболы представлен на рис.5.
б) Найдем проекции вектора ускорения на оси X и Y
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Обозначая
орты осей X
и Y
через
![]() и
и
![]() соответственно, запишем выражения для
векторов скорости и ускорения
соответственно, запишем выражения для
векторов скорости и ускорения
![]() ,
,
![]() .
.
Модули скорости и ускорения соответственно равны
![]() ,
,
![]() .
.
в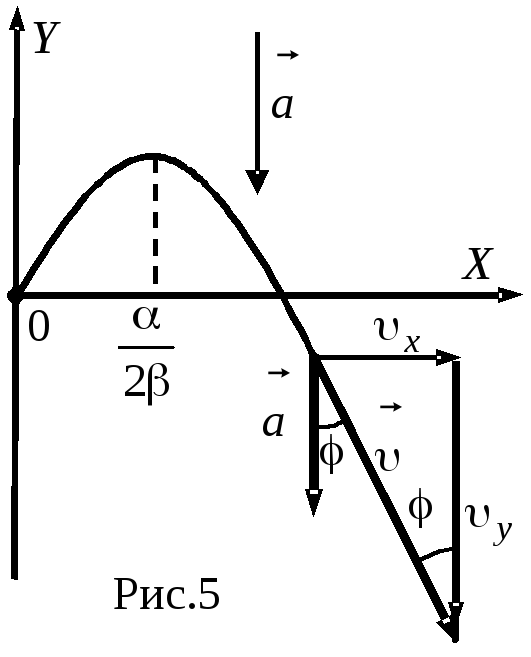 )
Покажем на рисунке направления векторов
)
Покажем на рисунке направления векторов
![]() и
и
![]() (рис.5). Для решения задачи удобно
воспользоваться способом нахождения
угла между скоростью и ускорением,
рассмотренным в задаче 1.4.
Согласно
результату этой задачи
(рис.5). Для решения задачи удобно
воспользоваться способом нахождения
угла между скоростью и ускорением,
рассмотренным в задаче 1.4.
Согласно
результату этой задачи
![]() .
.
Из
рисунка видно, что угол
![]() между скоростью и ускорением, может
быть равен
между скоростью и ускорением, может
быть равен
![]() ,
только для точек параболы, координаты
x
которых,
лежат правее ее вершины. Координату
,
только для точек параболы, координаты
x
которых,
лежат правее ее вершины. Координату
![]() вершины параболы найдем из условия
вершины параболы найдем из условия
![]() :
:
![]() ,
откуда
,
откуда
![]() .
.
Согласно
рисунку в области
![]() проекция скорости на ось Y
отрицательна
проекция скорости на ось Y
отрицательна
![]() ,
поэтому
,
поэтому
![]() .
.
По
условию угол
![]() ,
поэтому, подставив в последнее выражение
,
поэтому, подставив в последнее выражение
![]() ,
получим искомое время
,
получим искомое время
![]() .
.
1.7.
Точка движется в плоскости XY
по закону
![]() ,
,
![]() ,
где A
и
,
где A
и
![]() – положительные постоянные. Найти:
– положительные постоянные. Найти:
а) уравнение траектории;
б) Скорость, ускорение и их модули в зависимости от времени;
в)
путь S,
проходимой точки за время
![]() .
.
Решение. а) Чтобы найти уравнение траектории, исключим время t из исходных уравнений x(t) и y(t):
![]()
 ,
,
![]() .
.
![]() ,
,![]() .
.
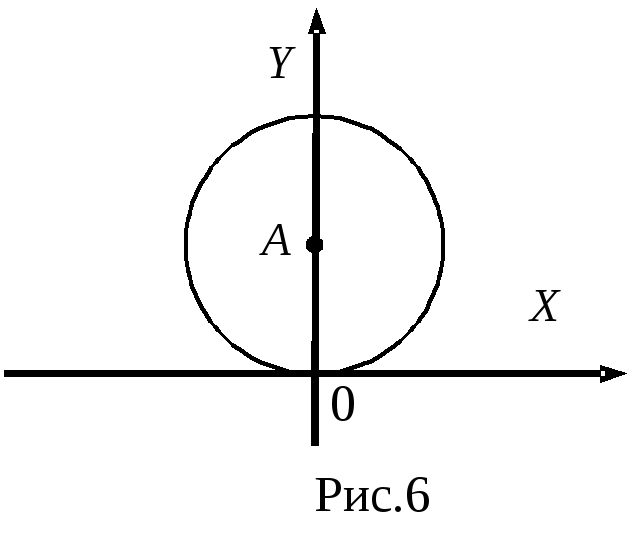
Уравнение траектории представляет собой окружность, центр которой имеет координаты (0,A). График функции y(x) в плоскости XY схематично изображен на рис.6.
б) Найдем проекции вектора ускорения на оси X и Y
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
Запишем выражения для векторов скорости и ускорения
![]() ,
,
![]() .
.
Тогда модули скорости и ускорения будут соответственно равны
![]() – const,
– const,
![]() – const.
– const.
Согласно полученным результатам, модули скорости и ускорения постоянны. Это значит, что точка движется по окружности с постоянной скоростью, а ускорение является центростремительным ускорением, направленным к центру окружности.
в)
Путь, пройденный телом, определяется
из определения модуля скорости
![]() как
как
![]() .
.
Итак, зная зависимость координат точки от времени, можно найти её скорость и ускорение. Эту же информацию можно получить, если известна траектория движения точки. Рассмотрим это на примере следующей задачи.
1.8.
Частица движется с постоянной по модулю
скоростью
![]() по плоской траектории
по плоской траектории
![]() ,
где
,
где
![]() .
Найти скорость и ускорение частицы в
точке x = 0.
.
Найти скорость и ускорение частицы в
точке x = 0.
Р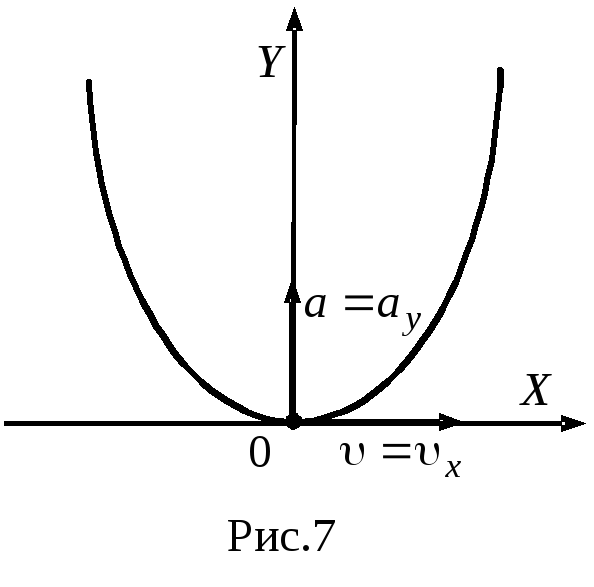 ешение.
Траектория
движения частицы - парабола с вершиной
в начале координат (рис.7).
ешение.
Траектория
движения частицы - парабола с вершиной
в начале координат (рис.7).
Продифференцировав
уравнение
![]() по времени, получим:
по времени, получим:
![]() или
или
![]() ,
,
т.е.
![]() при x = 0.
при x = 0.
Продифференцировав
по времени
![]() ,
найдем проекцию вектора ускорения на
ось Y
,
найдем проекцию вектора ускорения на
ось Y
![]() ,
,
но
![]() ,
значит
,
значит
![]() .
Поэтому
.
Поэтому
![]() .
.
Окончательно при x = 0:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
![]() .
.
