Множества чисел (натуральные, целые, рациональные, действительные). Комплексные числа, их свойства и действия над ними. Множество натуральных чисел

N = {1, 2, 3, ……} – множество натуральных чисел.

Обозначим буквой N₀ множество, состоящее из всех натуральных чисел и нуля. Так как через N мы обозначили множество всех натуральных чисел, то можно записать: N₀=N0, NN₀.

Рассмотрим уравнение х+а=b, a,bN₀.

Если аb, то существует единственное число c=baN₀, являющееся решением этого уравнения. Если же a>b, то во множестве N₀ уравнение не имеет решений. Чтобы для любых a,bN₀ существовало решение уравнения, надо расширить множество N₀. Такое расширение осуществляется добавлением к каждому числу а нового элемента, обозначаемого  а, так чтобы в сумме с а получался нуль:

( а)+а=0, а+( а)=0.

Этот новый элемент называется отрицательным числом, противоположным натуральному числу а (или обратным для a по сложению). Наоборот, положительное число а называется противоположным отрицательному числу -а.

Условимся числа изображать точками на прямой. Нулю соответствует фиксированная точка, называемая начальной или началом. Справа от начала с одинаковыми интервалами между двумя соседними числами, равными единице масштаба, располагаются натуральные числа, а слева от начала - отрицательные числа.

Множество целых чисел

Множество, состоящее из всех натуральных чисел, нуля и всех отрицательных чисел, называется множеством целых чисел и обозначается буквой Z (от немецкого слова "die Zahl" - число). Имеем: NN₀ Z.

Так как на числовой оси меньшее число располагается левее большего, то всякое отрицательное число меньше любого положительного числа и нуля. Запись m<0 означает, что m - отрицательное число.

Во множестве Z уравнение x+a=b всегда имеет единственное решение: х=b а.

Так как знак минус означает симметрию относительно начала, то

 ( а)=а, а b=а+( b), а (b с)=а b+с.

При умножении справедливы следующие правила знаков:

( а) b=а ( b)=(  а )b, ( а) ( b)=а b.

Правила арифметических действий над отрицательными числами легко выводятся из общих законов арифметических операций: переместительности (коммутативности) и сочетательности (ассоциативности) сложения и умножения, а также распределительности (дистрибутивности) умножения относительно сложения:

а+b=b+а, аb=bа, а+(b+с)=(а+b)+с, а(bс)=(аb)с, а(b+с)=аb+ас.

Отрицательные числа впервые появились в Древнем Китае. Уже в VI-XI веках они систематически употреблялись в Индии при решении задач. Однако, в европейской науке отрицательные числа получили окончательное признание лишь в XVII веке во времена Рене Декарта (1596-1650), давшего геометрическое истолкование чисел как направленных отрезков.

Рациональные числа

Рассмотрим уравнение ах=b, где а,b - целые числа, причем а 0. Если b делится на а без остатка, т.е. b=am, mZ, то во множестве целых чисел исходное уравнение имеет единственное решение х=m. В противном случае это уравнение не имеет решений во множестве Z. Чтобы уравнение имело решение при любых целых а и b при а 0, надо расширить множество Z, добавляя новые элементы 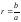, a,bZ, а 0.

Число 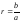называется рациональным числом или дробью с числителем b и знаменателем а. Если в рассматриваемое уравнение вместо х подставить , то получится тождество. Два рациональных числа считаются равными, если .

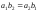Введение положительных рациональных чисел (дробей) явилось исторически первым расширением понятия натурального числа. Оно было вызвано тем, что не всегда единица измерения укладывается на измеряемой величине целое число раз. Дробные числа были уже известны в Древнем Египте и Вавилоне. Китайцы и индусы в начале новой эры уже производили над дробями все арифметические действия. Сначала пользовались единичными дробями, т. е. дробями 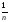с числителем единица. Дробь 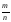определялась как сумма m одинаковых единичных дробей со знаменателем n. Лишь с развитием арифметики как науки о числе стали представлять дроби как отношение двух целых чисел, т.е. 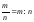. Отсюда и возникло название «рациональное число» от латинского «ratio» - отношение.

Положительная дробь называется правильной, если 0<m<n, т.е. если числитель меньше знаменателя, и неправильной, если m≥n>0. Применяя алгоритм деления, всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби:

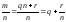, 0r<n.

Сумму 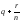символически записывают в виде 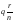и называют смешанной дробью с целой частью q. Дробь со знаменателем единица отождествляется с целым числом, равным числителю, т.е. 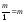. Если НОД(m,n)=1, то дробь 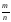называется несократимой.

Дробь 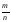называется десятичной, если ее знаменатель n является натуральной степенью числа 10. Для десятичной дроби употребляется особый вид записи. Например, вместо 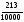, пишут: 0,0213. Дробь же, записанную в виде , где m и n - целые числа, n0, называют обыкновенной.

Десятичные дроби ввел в начале XVв. самаркандский математик аль-Каши, умерший около 1436 г., а в Европе они стали распространяться после выхода книги Симона Стевина (1548-1620) «Десятая» в 1585 г. В этой книге десятичные дроби стали составной частью унификации всей системы мер на десятичной основе.

Десятичные дроби, имеющие после запятой конечное число ненулевых цифр, называются конечными. Для их превращения в обыкновенные или смешанные дроби достаточно записать соответствующий знаменатель 10n, взяв числителем число из цифр после запятой и сохранив целую часть числа, если она есть. Например, число 2,023=2.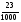

Десятичная дробь, имеющая сколь угодно много ненулевых цифр после запятой, называется бесконечной. Бесконечные десятичные дроби разбиваются на два класса - периодические, когда, начиная с некоторого момента, одна и та же группа цифр неограниченно повторяется, а других цифр, кроме этой группы, нет, и непериодические, если не существует такой бесконечно повторяющейся группы цифр после запятой. Повторяющуюся группу цифр в периодической десятичной дроби заключают в круглые скобки. Например, вместо 0,2353535... пишут 0,2(35).

Применяя алгоритм деления числителя на знаменатель, можно представить всякую обыкновенную дробь либо в виде конечной десятичной дроби (если простыми множителями знаменателя являются только двойки или пятерки), либо в виде бесконечной периодической (в остальных случаях). Например, .

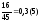Для того, чтобы периодическую десятичную дробь превратить в обыкновенную (или смешанную, если дробь больше единицы), надо в знаменателе дробной части записать слева направо столько девяток, сколько цифр в периоде, и столько нулей, сколько цифр до периода, а в числителе - разность между натуральным числом из цифр после запятой до второго периода и натуральным числом из цифр после запятой до первого периода.

Для доказательства этого утверждения умножим дробную часть х десятичной периодической дроби сначала на 10^k, где k - число цифр после запятой до второго периода, затем - на 10^h, где h - число цифр до первого периода. Вычитая из первого результата второй, получают справа натуральное число, равное числителю искомой обыкновенной дроби, а слева - указанный в теореме знаменатель, умноженный на данную дробную часть х. Целая же часть числа остается неизменной.

Рассмотрим, например, периодическую десятичную дробь 3,2(15). Здесь дробная часть х=0,2(15), k=3, h=1.

Имеем: 10³х  10х = 215  2. Следовательно, , а значит, .

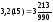Множество всех рациональных чисел обозначается буквой Q от латинского слова «quotient» - «частное».

Имеем: NN₀ Z Q.

Арифметические операции - сложение и умножение рациональных чисел удовлетворяют тем же законам ассоциативности, коммутативности и дистрибутивности, что и натуральных и целых чисел.

Заметим, что на числовой оси рациональные числа располагаются «всюду плотно», т.е. между любыми точками числовой прямой существует точка, изображающая рациональное число.

Рассмотрим на числовой прямой точку, являющуюся концом отрезка, равного диагонали квадрата, который построен на единичном отрезке этой прямой. Эту точку нельзя задать никаким рациональным числом. Действительно, предположим противное, т.е. что ей соответствует несократимая дробь 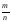, где m, n - ненулевые целые числа.

По теореме Пифагора получаем 1²+1²=2=, и далее m²=2n². Следовательно, m², а значит и m - числа четные, т.е. m=2k, kZ. Получаем: (2k)²=2n² Отсюда 2k²=n². Значит, n - тоже число четное, т.е. дробь оказалась сократимой. Пришли к противоречию.

Так как квадрат этого нового числа равен двум, то оно обозначается символом .

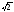Рассмотрим множество всех рациональных чисел, добавив к ним новые элементы, соответствующие тем точкам числовой оси, которые не изображают никакие рациональные числа. Каждый такой элемент называется иррациональным числом (от лат. «irrational» - безрассудный, не определяемый отношением).

Множество всех рациональных и иррациональных чисел образует новое множество, называемое множеством действительных чисел. Оно обозначается буквой R ( от фр. «r ee l» - действительный, реальный).

Всякому действительному числу соответствует единственная точка на числовой прямой. Наоборот, всякой точке на числовой прямой соответствует единственное действительное число.

Имеем: NN₀ Z Q R.

Пусть х - произвольное действительное число. Откладывая от начала координат единичный отрезок в положительном (при х≥0) или отрицательном (при х<0) направлении, убеждаемся, что существует единственное целое число n такое, что

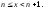
Если x=n, то процесс закончен. Если же х>n, то, разбивая единичный отрезок на 10 частей и откладывая от точки n в положительном направлении десятые доли, получим:

n,n₁ x< n,(n₁+1).

Продолжая, в случае неравенства, процесс откладывания сотых, тысячных и т.д. частей, убеждаемся, что всякое действительное число либо совпадает с конечной десятичной дробью, либо выражается бесконечной десятичной дробью, лежащей с любой степенью точности между двумя конечными десятичными дробями. При этом конечная и бесконечная периодическая десятичная дробь является рациональным числом, а бесконечная непериодическая десятичная дробь - иррациональным числом.

Операции сложения и умножения иррациональных чисел осуществляются путем предельного перехода результатов соответствующих операций над конечными десятичными дробями, являющимися приближениями исходных чисел. Например, для нахождения суммы составляют монотонно возрастающую ограниченную сверху последовательность десятичных дробей:

1,4+1,7=3,1;

1,41 + 1,73=3,14;

1,414+1,732=3,146;

1,4142+1,7320=3,1462;

1,41421+1,73205=3,14626;

1,414213+1,732050=3,146263,

1,4142135+1,7320508=3,1462643; и т.д. В пределе эта последовательность и дает число .

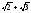Арифметические операции над действительными числами удовлетворяют тем же законам ассоциативности, коммутативности, дистрибутивности, что и над рациональными числами.

Знак минус перед действительным числом означает переход к противоположному числу, изображаемому симметричной относительно начала числовой прямой точкой. Следовательно,

-(-х)=х для любого xR.

Модулем действительного числа х называется число, равное х, если x ≥0, и равное -х, если х<0. Обозначается |х|. Например, |5|=5, |-7|=7, |0|=0. Геометрически модуль х есть расстояние от точки х до начала числовой прямой. Очевидно, |x|>0, |х+y|  |х|+|y|.

Кроме того, (-х)у=х(-у)=-ху, (-х)(-у)=ху .

Научная теория действительных чисел исчерпывающе была разработана немецкими математиками Вейерштрассом(1815-1897) и Дедекиндом(1831-1916).