3.1.2. Собственные колебания

Собственными колебаниями называются движения, совершаемые колебательной системой, которая после кратковременного внешнего возмущения представлена самой себе. При этом происходят периодические переходы одного вида энергии в другой. Если сумма энергий в процессе колебаний сохраняется, то колебания будут незатухающие и система называется консервативной, если энергия уменьшается, то система - неконсервативная. Кроме того, можно разделить системы на линейные и нелинейные.

Типичными консервативными колебательными системами являются масса, колеблющаяся на пружине, RC электрический колебательный контур, резонатор Гельмгольца, крутильные осцилляторы, гравитационный маятник и т. п. Такие системы описываются линейными или обыкновенными нелинейными дифференциальными уравнениями второго порядка. При этом задаются начальные условия, т.е. для них решается задача Коши. В большинстве случаев уравнение имеет вид:

, (3.1.10)

где х и t – координата положения и время движения тела [III, 9, 12].

При наличии сопротивления или потерь энергии консервативность нарушается. Это описывается введением в уравнение первой производной искомой функции и уравнение в общем случае приобретает вид:

. (3.1.11)

Для упрощения решения таких уравнений и удобства интерпретации и исследования полученных данных дифференциальное уравнение второго порядка приводят к системе двух дифференциальных уравнений первого порядка:

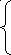
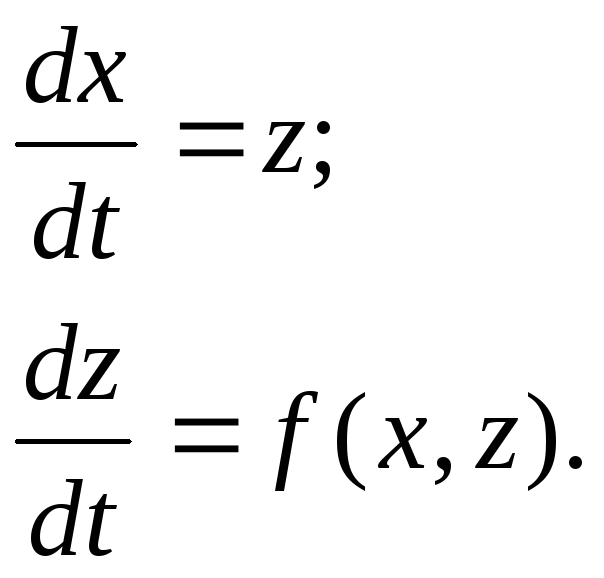(3.1.12)

В уравнениях такого рода независимая переменная не входит явно в уравнения (или систему), и такую систему называют автономной [III, 14-15].

1. Автономные линейные системы.

В общем случае их можно записать в виде:

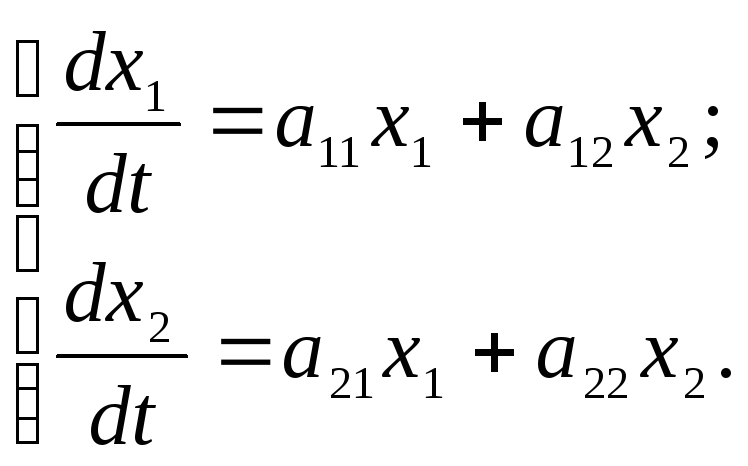(3.1.13)

Для таких систем характерно наличие точки покоя. При этом характер точки покоя (ее устойчивость, асимптотическую устойчивость, неустойчивость) определяется по значениям собственных чисел матрицы А коэффициентов правой части системы. Предполагается, что определитель матрицы А не равен нулю, т. е. матрица невырожденная. Собственные числа находятся из характеристического уравнения:

или . (3.1.14)

Возможны случаи:

А) Корни  действительны и различны. При этом:

1) оба корня , отрицательны – точка покоя устойчива и называется устойчивым узлом;

2) оба корня , положительны - точка покоя называется неустойчивым узлом;

3) оба корня , действительные числа разных знаков – точка покоя неустойчива и называется седлом;

4) - точка покоя специального вида, называемая диакритический узел. Если а) - точка покоя устойчива;

б) - точка покоя неустойчива;

5) если и , то существует прямая, проходящая через начало координат, все точки которой – точки покоя;

6) все точки плоскости – точки покоя.

Б) Корни характеристического уравнения комплексны, т.е. .

Тогда:

1) если p > 0, то точка покоя – устойчивый фокус;

2) если p < 0, то точка покоя – неустойчивый фокус;

3) если p = 0, a , то решение является периодическим, а точка покоя называется центром.

Если записать решение в параметрической форме, то на плоскости, которую называют фазовой, можно представить фазовые траектории решения системы. В трехмерном пространстве можно построить интегральные кривые. Фазовую траекторию задают уравнения:

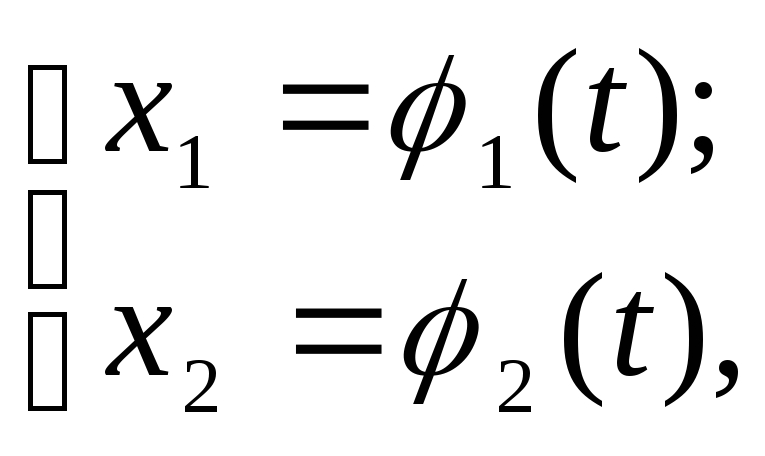(3.1.15)

а интегральную кривую -

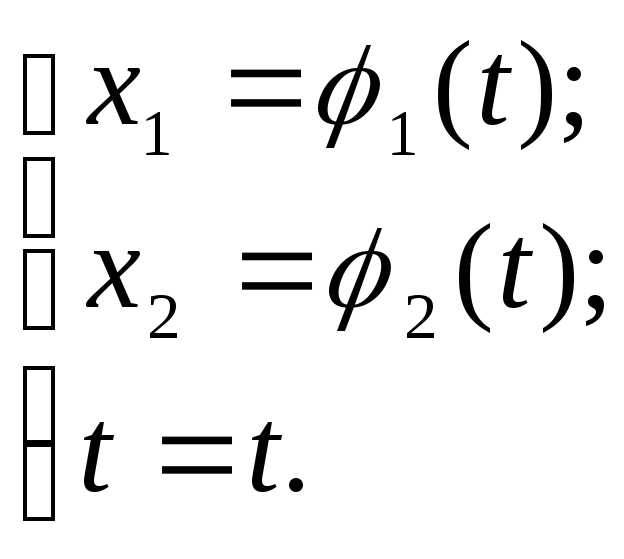(3.1.16)

Для нелинейных систем вводится понятие предельных циклов, которые бывают трех типов:

1) устойчивые;

2) неустойчивые;

3) полуустойчивые.

Если записать автономную систему в векторной форме:

, (3.1.17)

то автономная система полностью определяется заданием векторного поля F(X).

По данной теме предполагается проведение двух лабораторных работ:

1) Исследование автономной линейной системы.

2) Исследование автономной нелинейной системы.

Физический смысл задач подбирается исходя из специализации студентов, после чего уравнения приводятся к стандартному математическому виду.

Решения такого рода задач удобно проводить, используя встроенные функции пакета MathCAD. Решить задачу Коши для таких систем можно с помощью функций:

rkfixed(y, x1, x2, n, D) – решение задачи на отрезке методом Рунге – Кутты с постоянным шагом;

Rkadapt(y, x1, x2, n, D) – решение задачи на отрезке методом Рунге – Кутты с автоматическим выбором шага;

Stiffbkadapt(y, x1, x2, n, D, J) – решение задачи на отрезке методом Булирша-Штера,

здесь y – вектор начальных условий; x1, x2 – левый и правый концы рассматриваемого интервала; n – число участков разбиения интервала; D и J – вектор-функция и якобиан правой части исходной системы уравнений.