2.6.5. Вопросы для самопроверки
1. Каково условие сходимости итерационного процесса в векторном виде?
2. Запишите условие сходимости итерационного процесса в координатном виде.
3. К чему сводится условие локализации корня и зачем оно нужно?
Лабораторная работа № 2.7 (С:\USERS\GROUP\NOF\lab7.mcd)
Численное интегрирование:метод прямоугольников и трапеций, формула симпсона
2.7.1. Цель работы. Получение практических навыков алгоритмизации и программирования приближенного вычисления определенных интегралов с применением шаблонов определенных интегралов и сумм.
2.7.2. Справочный материал. Пусть подынтегральная функция f(x) определена на отрезке [a,b], разобьем его на N равных частей, т. е. введем равномерную пространственную сетку
a = x0 < x1 < x2 < …< xN-1 < xN = b, (2.7.1)
где N+1- число пространственных узлов; xi = i h; h = (b - a) / N; i = 0, 1,…, N.
На отрезке [a,b] определенный интеграл, геометрический смысл которого – площадь фигуры ограниченной кривой f(x) и прямыми У = 0, Х = а, Х = b, приближенно можно вычислить по ряду формул, которые аппроксимируют определенный интеграл с различной точностью. Так, например, простейшая формула прямоугольников, в основе которой лежит аппроксимация всей площади фигуры площадями элементарных прямоугольников f(a)·h, f(x1)·h, … , f(xN-1)·h, имеет первый порядок точности 0(h)
или
.
(2.7.2)
Формула трапеций, основанная на площадях элементарных трапеций (f(a)+f(x1))/2·h, (f(x1)+f(x2))/2·h, … , (f(xN-1)+f(b))/2·h, имеет второй порядок точности 0(h2)
.
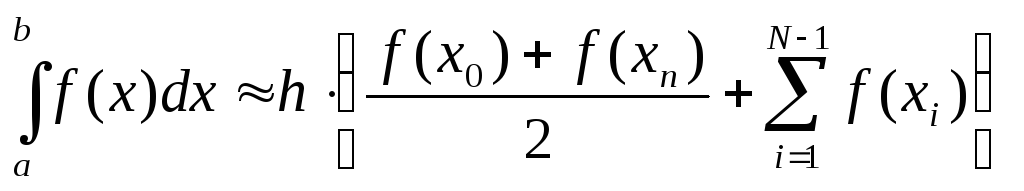(2.7.3)
Формула Симпсона аппроксимирует определенный интеграл с третьим порядком точности 0(h3)
.
(2.7.4)
Формула Симпсона (2.7.4) получается если подынтегральную функцию f(x) на паре элементарных интервалов [xi-1,xi+1] аппроксимировать параболой.
Точность полученного значения определяется числом элементарных площадок Si, т.е. числом узлов сетки.
2.7.3. В качестве примера возьмем подынтегральную функцию вида:
, на отрезке [0,8; 1,4].
Для уточнения эффективности методов прямоугольника и трапеции зададимся точностью вычисления определенного интеграла, равной δ = 1%, в зависимости от числа узлов разностной сетки
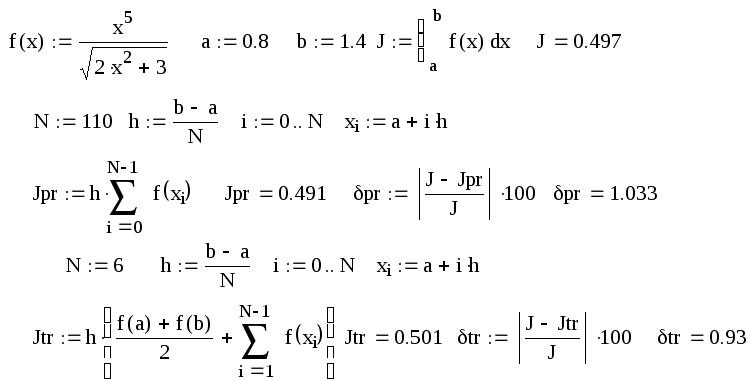
Итак, для метода прямоугольника отрезок [a,b] пришлось разбить на 110 частей, чтобы вычислить определенный интеграл с точностью 1%, а в методе трапеций потребовалось разбить всего на шесть частей.
2.7.4. Задание. Приводим варианты заданий для приближенного вычисления интегралов.
