2.7.5. Вопросы для самопроверки
1. Напишите формулы прямоугольников.
2. Напишите формулу трапеций.
Лабораторная работа № 2.8 (С:\USERS\GROUP\NOF\lab8.mcd)
Численное решение обыкновеНноГо дифференциального уравнениЯ МетодОм эЙлера и рунге-кутта
2.8.1. Цель работы. Получение практических навыков алгоритмизации и программирования численного решения обыкновенного дифференциального уравнения методом Эйлера и Рунге-Кутта.
2.8.2. Справочный материал. Простейшим обыкновенным дифференциаль-ным уравнением является уравнение первого порядка
y’ = f(x,y), xa,b. (2.8.1)
Основная задача, связанная с уравнением (2.8.1), известна как задача Коши: найти решение дифференциального уравнения в виде функции у(х), удовлетворяющей начальному условию
у(х0) = у0. (2.8.2)
Для численного решения обыкновенного дифференциального уравнения (2.8.1) методом Эйлера и Рунге-Кутта разобьем отрезок [a,b] на N равных частей, т.е. введем равномерную пространственную сетку
a = x0 < x1 < x2 < …< xN-1 < xN = b, (2.8.3)
где N+1- число пространственных узлов; xi = i h; h = (b - a) / N; i = 0, 1, .. , N.
На основании определения производной от функции у(х) запишем
.
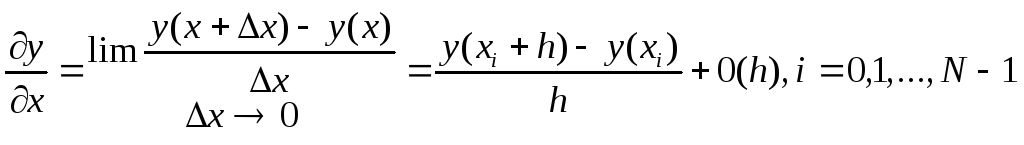(2.8.4)
Равенство в выражении (2.8.4) предполагает использование предельного перехода
h = (b – a)/N, при N → ∞.
При численной реализации разностных производных исходят из того факта, что любые измерения величин имеют свои погрешности и численные расчеты этих величин должны иметь такие же погрешности, что и определяет конечные значения N.
Первый порядок точности 0(h) для правой разностной производной (2.8.4) может быть установлен с помощью ряда Тейлора.
В дальнейшем будут использованы следующие обозначения:
yi-1 = y(xi –h); yi = y(xi); yi+1 = y(xi + h). (2.8.5)
Левая, как и правая разностная производная имеет первый порядок точности, центральная - второй
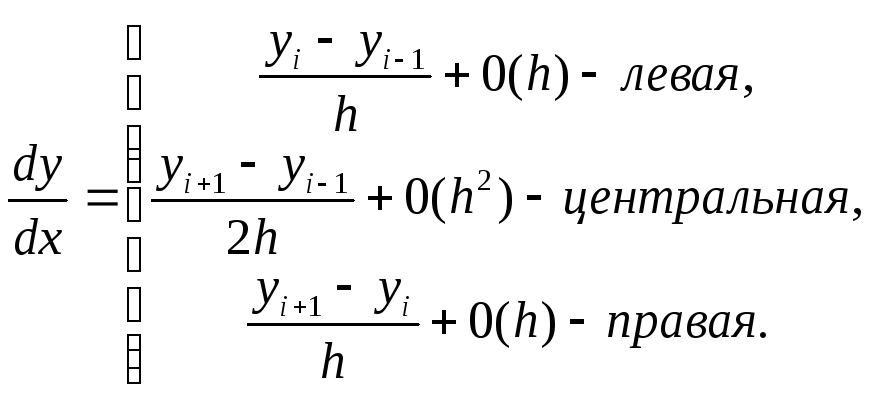(2.8.6)
Разностная схема по методу Эйлера для задачи Коши (2.8.1) записывается следующим образом:
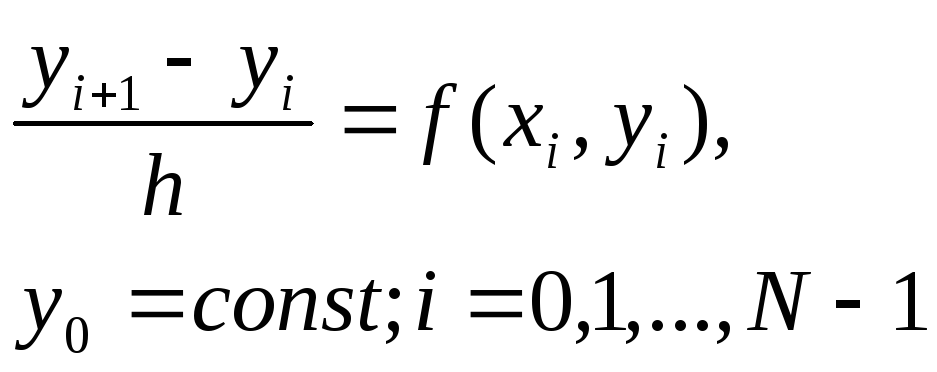или
.
(2.8.7)
Таким образом, метод Эйлера достаточно прост, но имеет первый порядок точности 0(h). Поэтому в методе Рунге-Кутта он рассматривается как первый этап - предикация (предсказание, т.е. приближенное решение). На втором этапе это решение корректируется на основе разностной схемы второго порядка точности 0(h2)
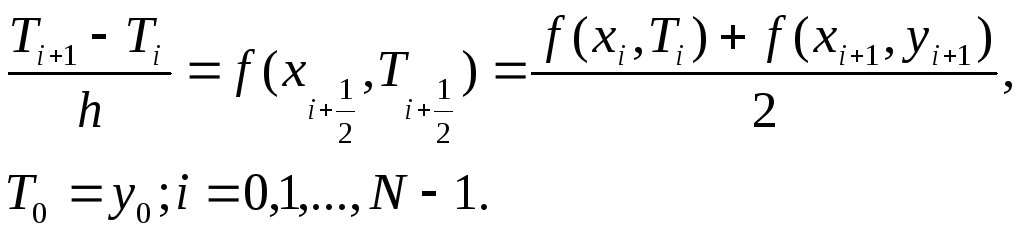(2.8.8)
В данном случае правая разностная производная становится центральной относительно полуцелой точки i+1/2, а значение уi, вычисленное на первом этапе, используется при вычислении правой части (2.8.8).
2.8.3.Пример. Проинтегрировать обыкновенное дифференциальное уравнение
x0,5;
1,5
(2.8.9)
с начальным условием у(0,5) = 0,724.
С целью анализа эффективности разностной схемы Эйлера, беря за истинное значение функции значение TN, вычисленное по схеме второго порядка точности 0(h2), определим, при каком числе элементарных отрезков N значения функций будут совпадать с точностью 2% на правом конце счетной области.
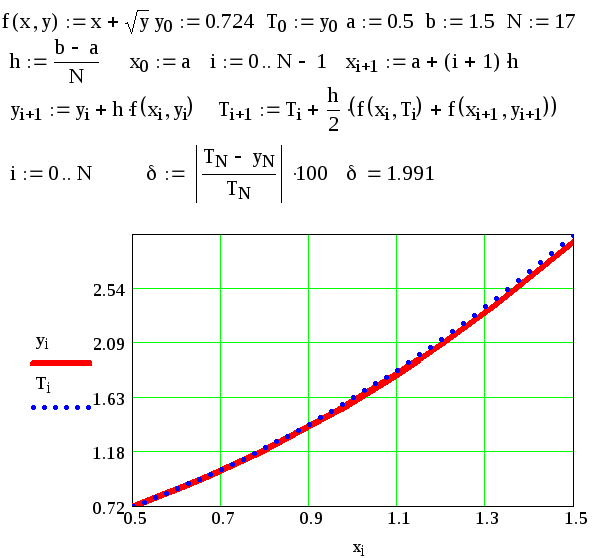
Рис. 2.8.1. Пространственное распределение значений функций у и Т,
вычисленных по схемам первого (сплошная кривая) и второго порядков точности
Таким образом, для дифференциального уравнения (2.8.9) метод Эйлера при разбиении на N = 17 частей счетной области дает приемлемые результаты.
2.8.4. Задание. В табл. 2.8.1 приведены варианты заданий для решения уравнения y’ = f(x,y), xa,b с начальным условием у0 = у(а).
Таблица 2.8.1
|
№ п/п |
f(x,y) |
a |
b |
Y(a) |
|
1 |
y·cos(x) |
0 |
1 |
1 |
|
2 |
y3/(x+1) |
0 |
1 |
1 |
|
3 |
0.5·x·y |
0 |
1 |
1 |
|
4 |
x2 + y2 |
0 |
1 |
0 |
|
5 |
1 + x·y2 |
0 |
1 |
0 |
|
6 |
0.1/x2 – y2 |
1 |
2 |
1 |
|
7 |
1+ y·sin(x) – y2 |
0 |
1 |
0 |
|
8 |
1/x2 y/x – y2 |
1 |
2 |
1 |
|
9 |
x + y |
0 |
1 |
1 |
|
10 |
y - 2·x/y |
0 |
1 |
1 |