
- •Тема 1. Неопределеный интеграл
- •1.1. Первообразная функция и неопределенный интеграл. Таблица основных интегралов
- •Свойства неопределенного интеграла
- •1.2. Основные методы интегрирования
- •Задание 1
- •Тема 2. Определеный интеграл и его приложения
- •Задание 2
- •Тема 3. Несобственные интегралы
- •Задание 3
- •Тема 4. Двойной интеграл
- •Основные свойства двойного интеграла
- •Правила вычисления двойных интегралов
- •Задание 4
- •Задание 5
- •Тема 5. Дифференциальные уравнения
- •5.1. Дифференциальные уравнения (ду). Основные понятия и определения
- •5.2. Дифференциальные уравнения первого порядка
- •5.3. Дифференциальные уравнения второго порядка, допускающие понижение порядка
- •5.4. Линейные дифференциальные уравнения второго порядка
- •Задание 6
- •Задание 7
- •Задание 8
- •Тема 6. Ряды
- •6.1. Числовые ряды. Необходимый признак сходимости
- •6.2. Достаточные признаки сходимости знакоположительных рядов
- •1. Признаки сравнения
- •2. Признак Даламбера
- •3. Радикальный признак Коши
- •4. Интегральный признак Коши
- •6.3. Абсолютная и условная сходимость знакопеременных рядов
- •Признак Лейбница (достаточный признак сходимости знакочередующихся рядов)
- •6.4. Степенные ряды
- •Задание 9
- •Задание 10
- •Литература
- •Оглавление
- •Тема 1. Неопределеный интеграл 4
Задание 2
2.1.
Найти площадь фигуры, ограниченной
линиями
![]() .
.
2.2.
Найти длину дуги линии
![]() .
.
2.3.
Найти площадь фигуры, ограниченной
линиями
![]() .
.
2.4.
Найти длину дуги линии
![]() ,
отсеченной прямой
,
отсеченной прямой
![]() .
.
2.5.
Найти объем тела, полученного вращением
фигуры Ф:
![]() вокруг оси Ох.
вокруг оси Ох.
2.6.
Найти площадь фигуры, образованной
линиями
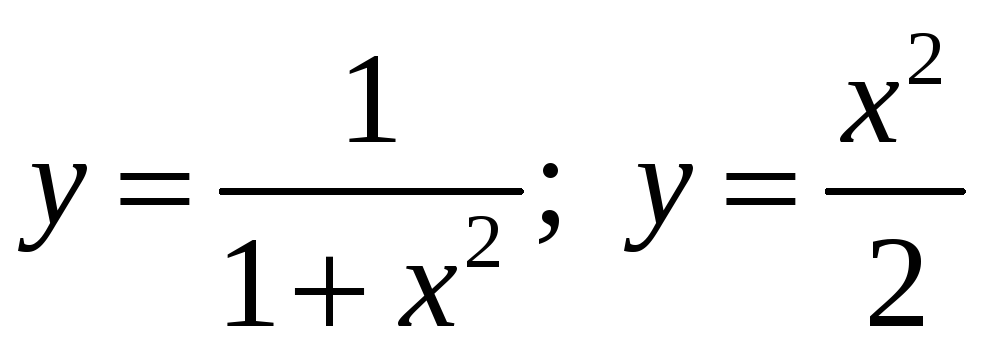 .
.
2.7.
Найти длину дуги линии
![]()
![]() .
.
2.8.
Найти объем тела, полученного вращением
фигуры Ф:
![]() вокруг оси Ох.
вокруг оси Ох.
2.9.
Найти площадь фигуры, ограниченной
линиями
![]() .
.
2.10.
Найти длину дуги линии
![]()
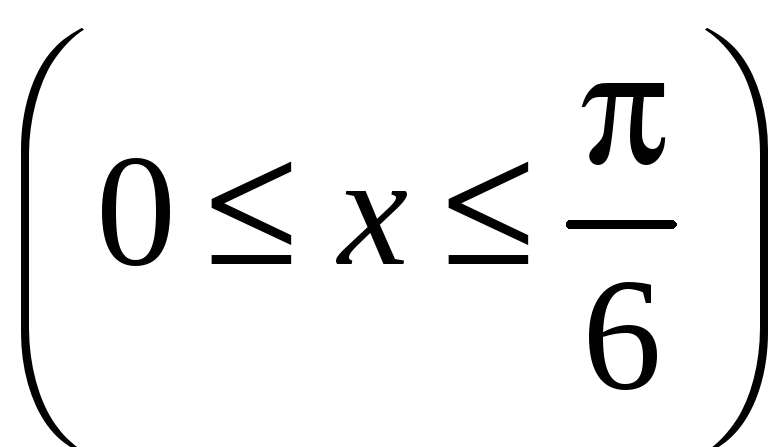 .
.
2.11.
Найти объем тела, полученного вращением
фигуры Ф:
![]()
![]() вокруг оси Ох.
вокруг оси Ох.
2.12.
Найти площадь фигуры, ограниченной
линиями
![]() .
.
2.13.
Найти длину дуги линии
![]()
![]() .
.
2.14.
Найти объем тела, полученного вращением
фигуры Ф:
![]() вокруг оси Oy.
вокруг оси Oy.
2.15.
Найти площадь фигуры, ограниченной
линиями
![]() .
.
2.16.
Найти длину дуги линии
![]() от точки А(
0; 0) до точки В(
4; 8).
от точки А(
0; 0) до точки В(
4; 8).
2.17.
Найти объем тела, полученного вращением
фигуры Ф:
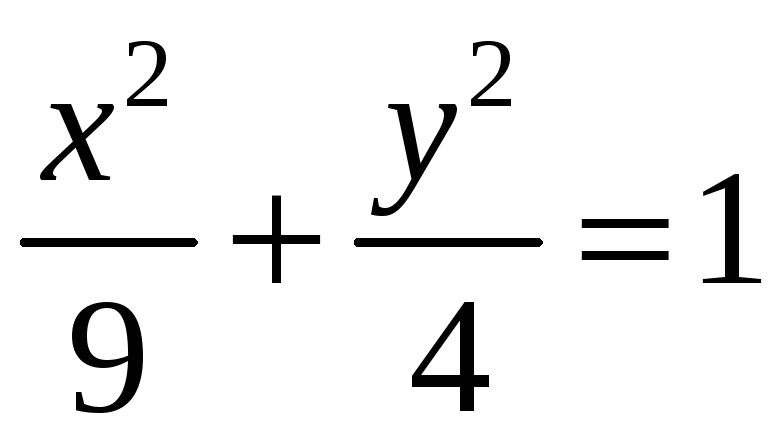 вокруг оси Ох.
вокруг оси Ох.
2.18.
Найти площадь фигуры, ограниченной
линиями
![]() .
.
2.19.
Найти длину дуги линии
![]() (петля).
(петля).
2.20.
Найти объем тела, полученного вращением
фигуры Ф:
![]() вокруг оси Oх.
вокруг оси Oх.
2.21.
Найти площадь фигуры, ограниченной
линиями
![]() .
.
2.22.
Найти длину дуги линии
![]()
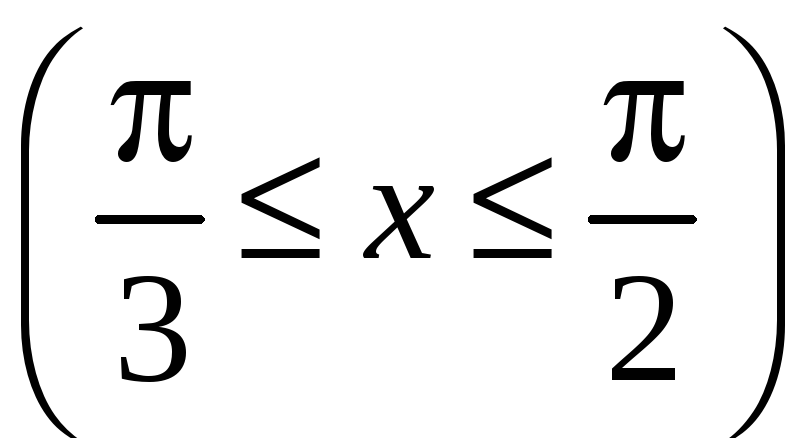 .
.
2.23.
Найти объем тела, полученного вращением
фигуры Ф:
![]() вокруг оси Oх.
вокруг оси Oх.
2.24.
Найти площадь фигуры, ограниченной
линиями
![]() .
.
2.25.
Найти длину дуги линии
![]() ,
,![]() .
.
2.26.
Найти объем тела, полученного вращением
фигуры Ф:
![]() вокруг оси Oх.
вокруг оси Oх.
2.27.
Найти площадь фигуры, ограниченной
линиями
![]() .
.
2.28.
Найти длину дуги линии
![]() ,
,
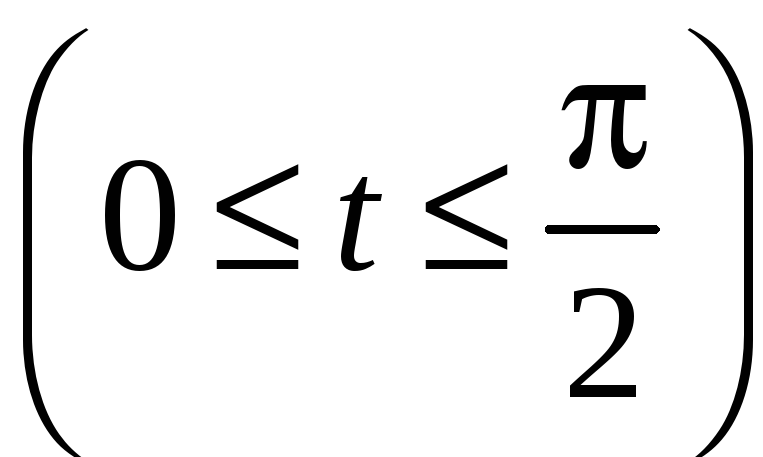 .
.
2.29.
Найти объем тела, полученного вращением
фигуры Ф:
![]() вокруг оси Ох.
вокруг оси Ох.
2.30.
Найти площадь фигуры, ограниченной
линиями
![]() .
.
Тема 3. Несобственные интегралы
Пусть функция
![]() определена на
определена на
![]() и интегрируема на любом отрезке
и интегрируема на любом отрезке
![]() .
Тогда
.
Тогда
 называется несобственным
интегралом от функции
называется несобственным
интегралом от функции
![]() в пределах от
в пределах от
![]() до
до
![]() и обозначается
и обозначается
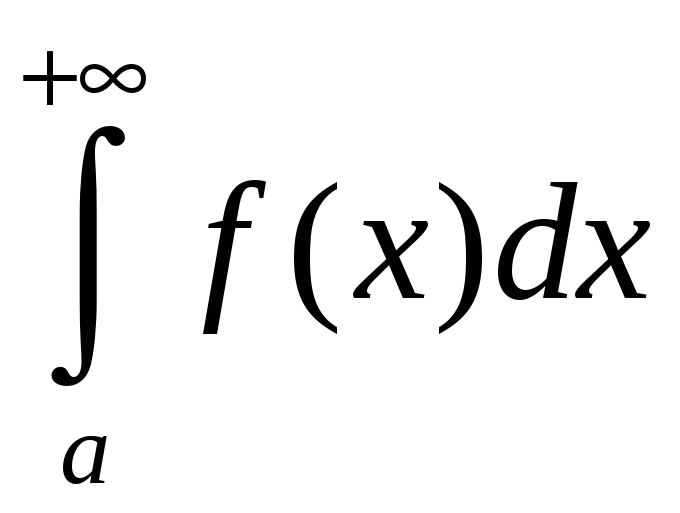 .
Таким образом
.
Таким образом
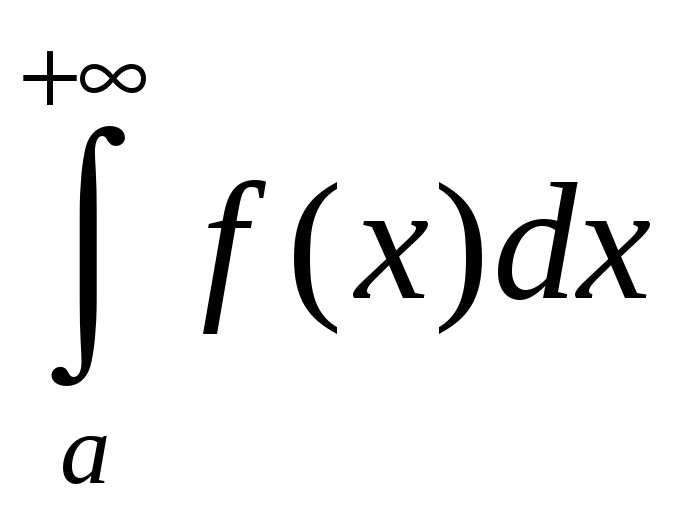 =
=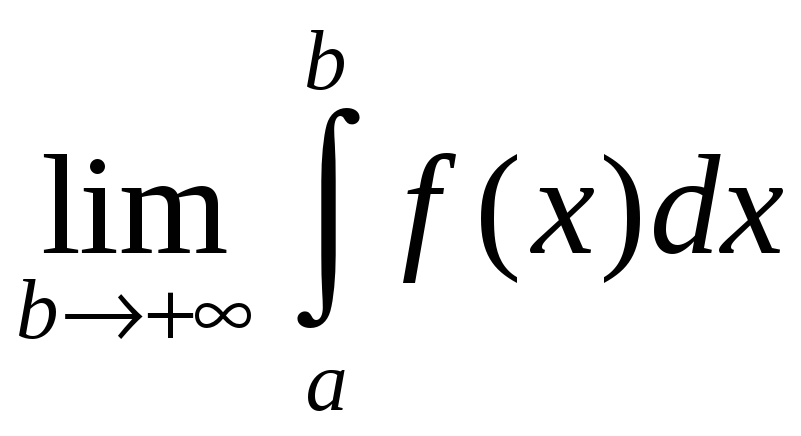 . (3.1)
. (3.1)
Аналогично определяются интегралы
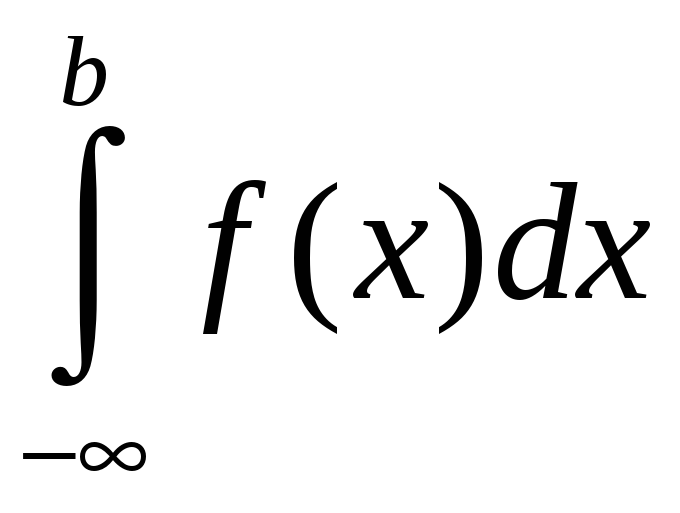 =
=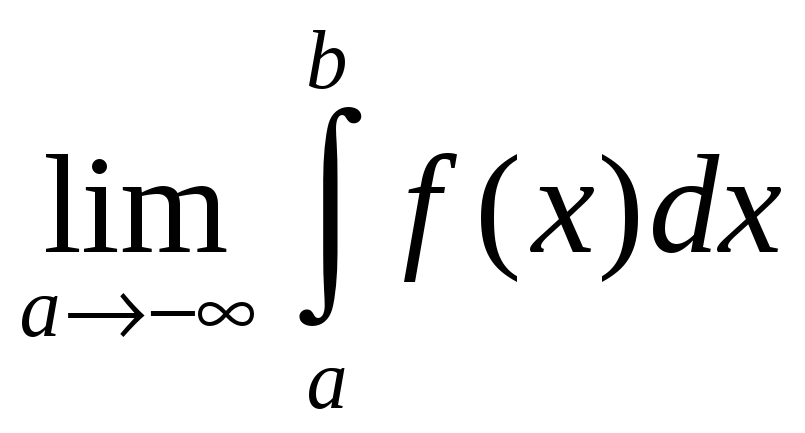 . (3.2)
. (3.2)
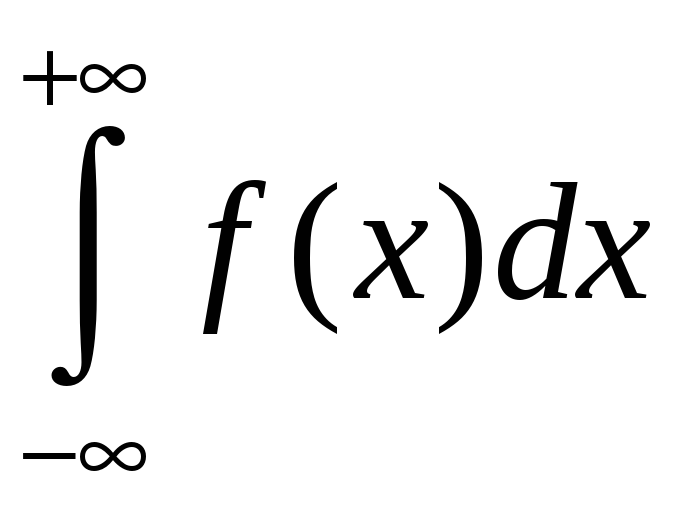 =
=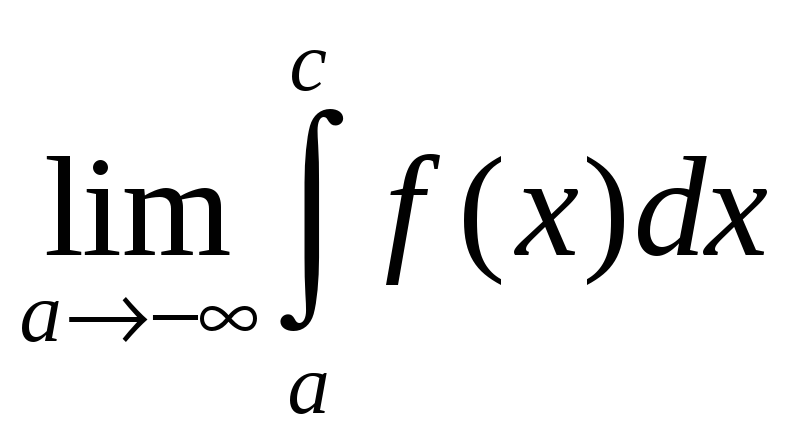 +
+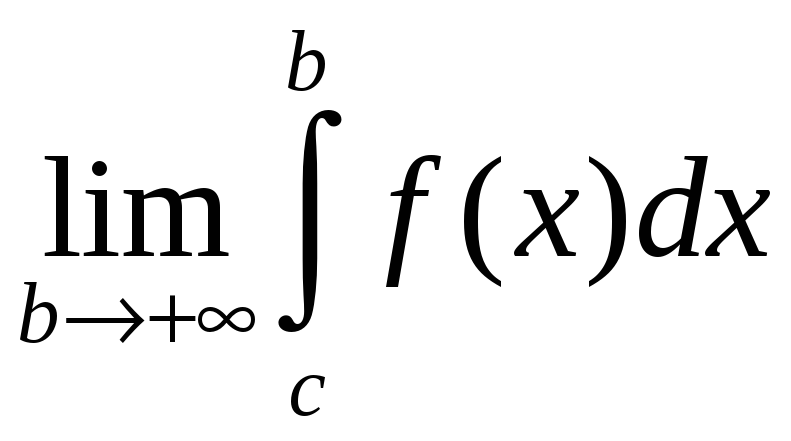 . (3.3)
. (3.3)
(с
– любая точка интервала
![]() ,
чаще
,
чаще
![]() ),
где
),
где
![]() независимо друг от друга.
независимо друг от друга.
Если приведенные пределы существуют и конечны, то соответствующие интегралы называют сходящимися. В противном случае интегралы называются расходящимися.
Признак сравнения.
Если
![]() ,
то из сходимости интеграла
,
то из сходимости интеграла
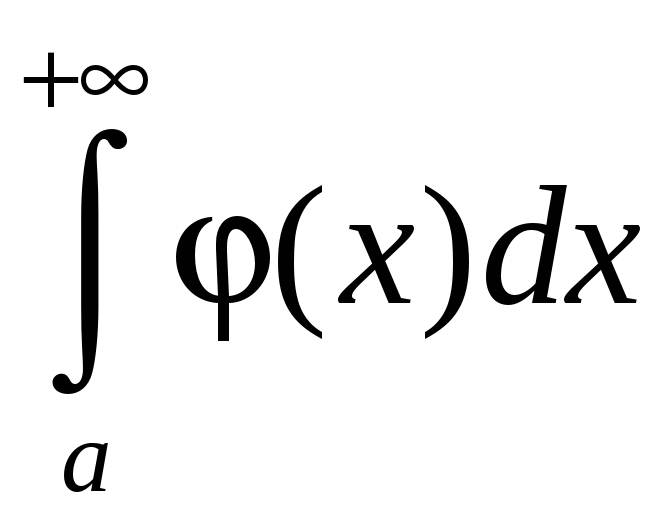 следует сходимость
следует сходимость
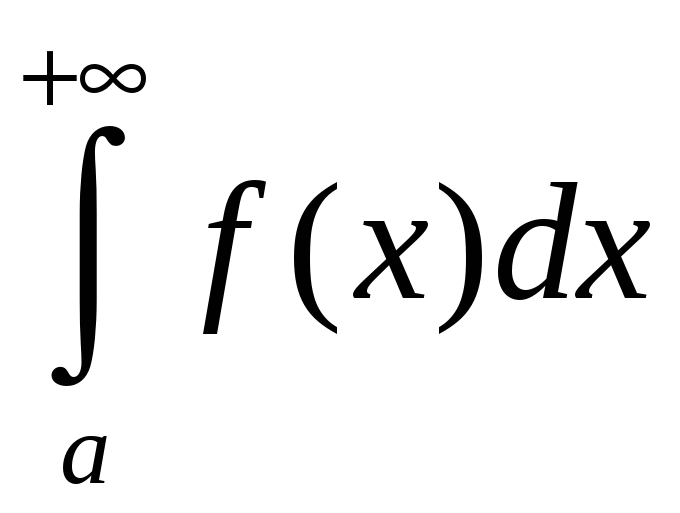 ,
а из расходимости интеграла
,
а из расходимости интеграла
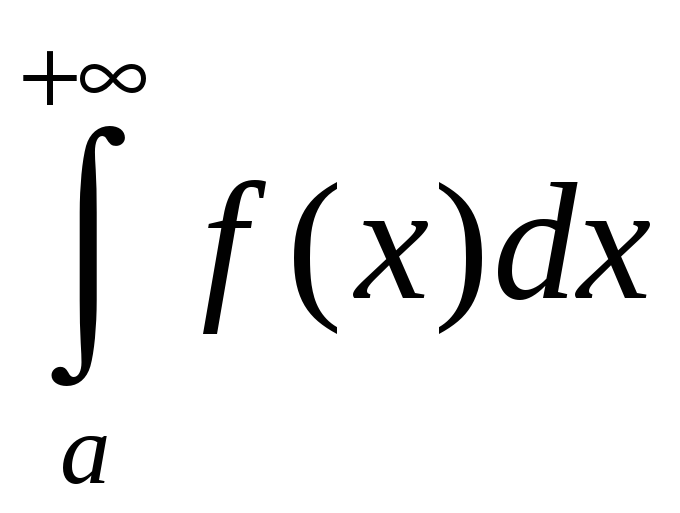 – расходимость интеграла
– расходимость интеграла
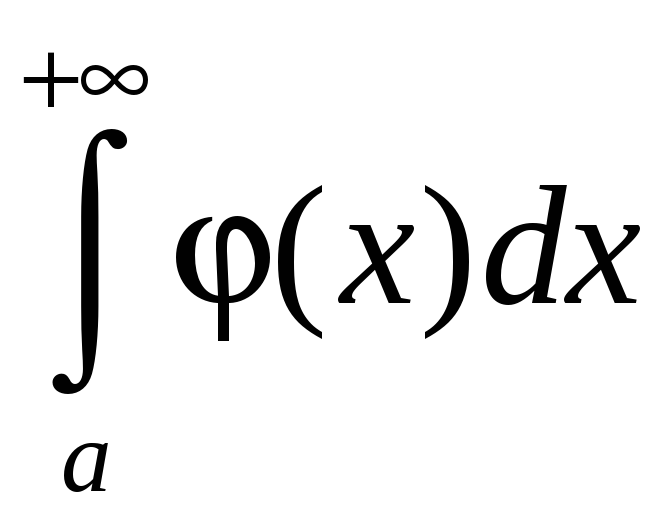 .
.
Пример 3.1. Вычислить несобственный интеграл или установить его расходимость:
а)
 ; б)
; б)
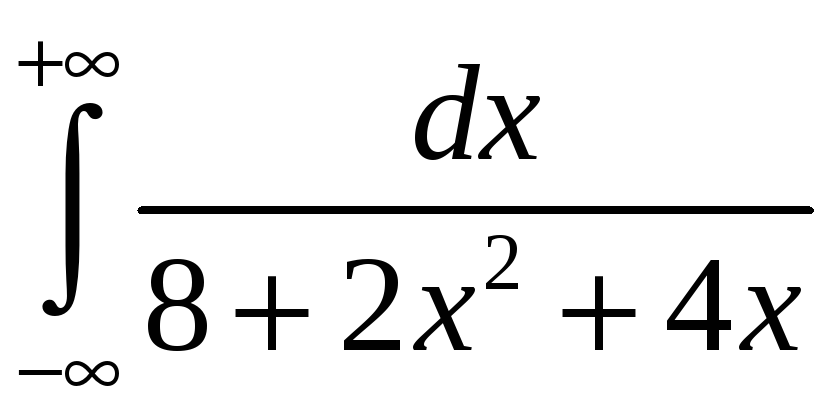 .
.
Решение.
а) Воспользуемся формулой (3.1):
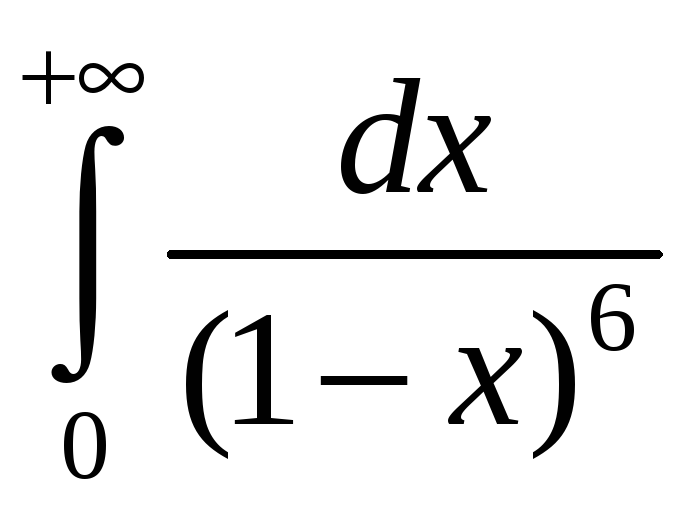 =
=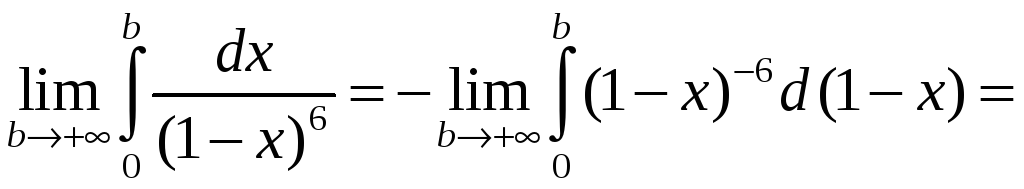
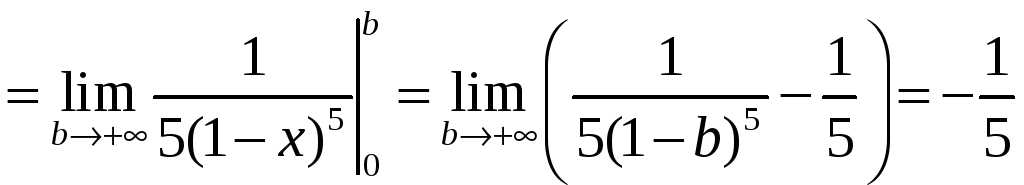 .
.
б) Согласно формуле (3.3)
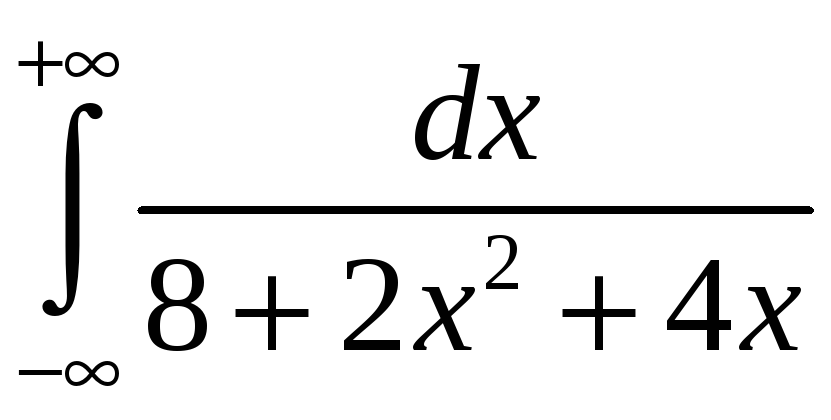 =
=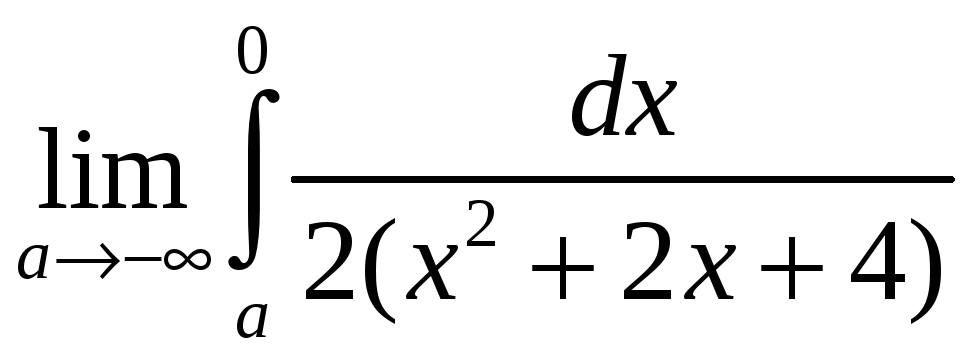 +
+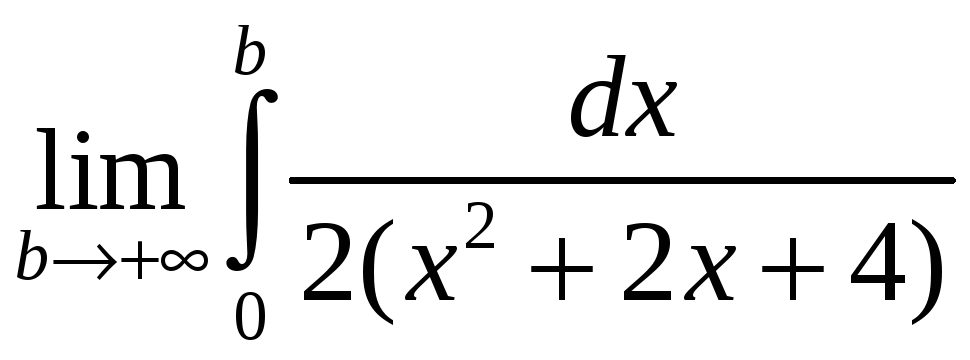 =
=
=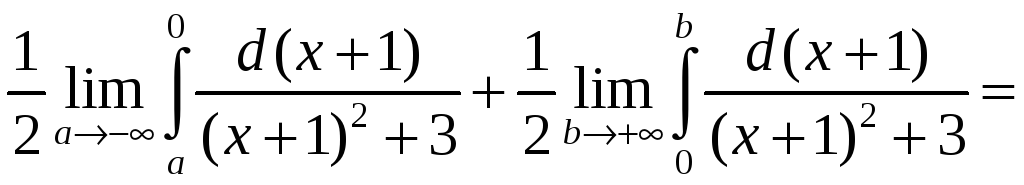
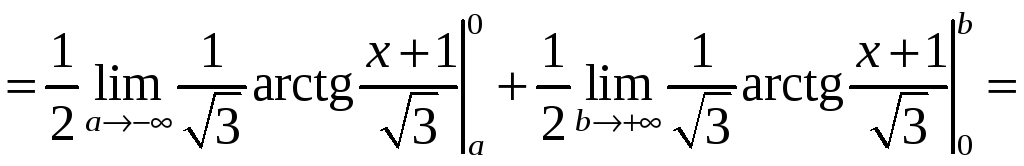
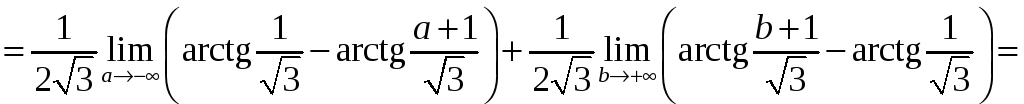
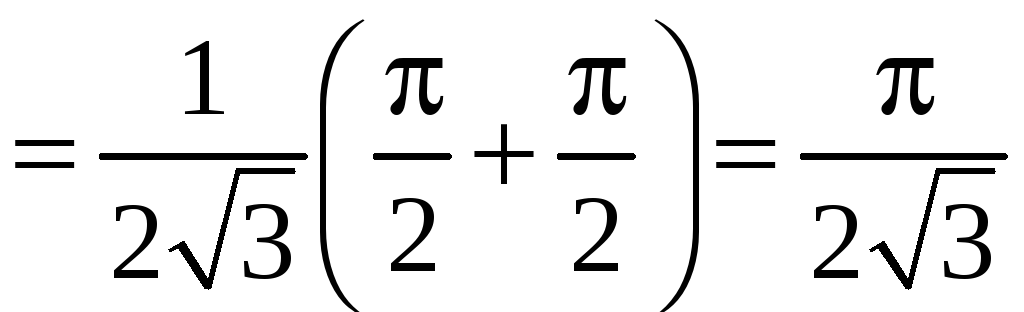 .
.
Задание 3
Вычислить несобственный интеграл или установить его расходимость.
3.1.
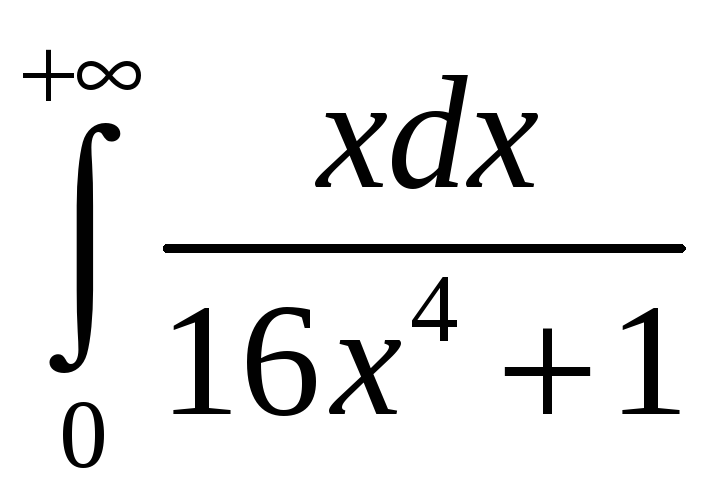 . 3.2.
. 3.2.
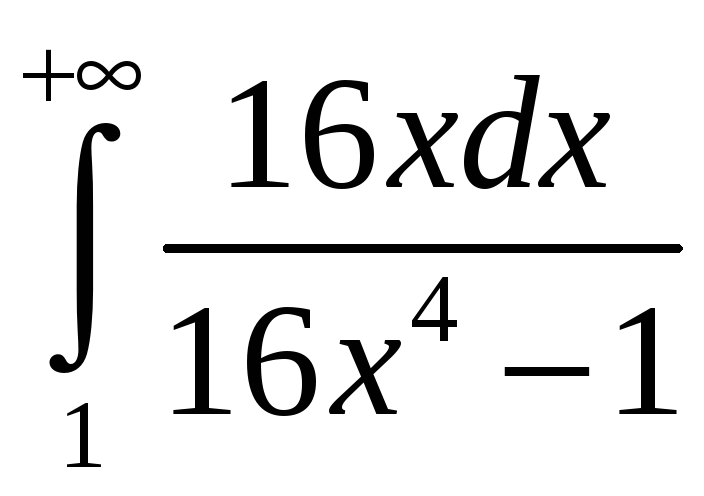 . 3.3.
. 3.3.
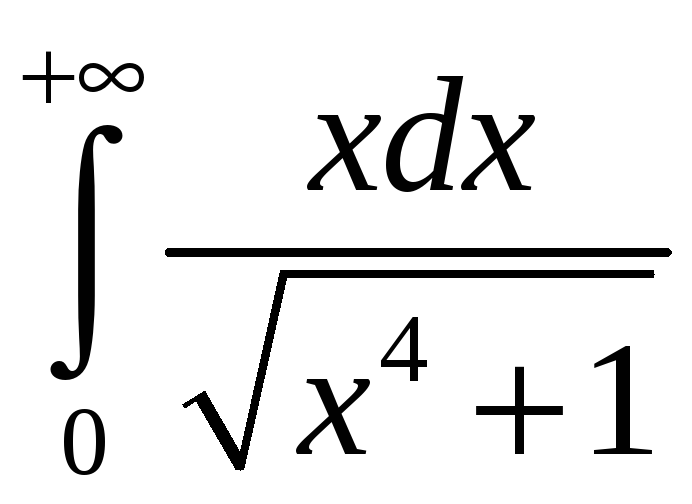 .
.
3.4.
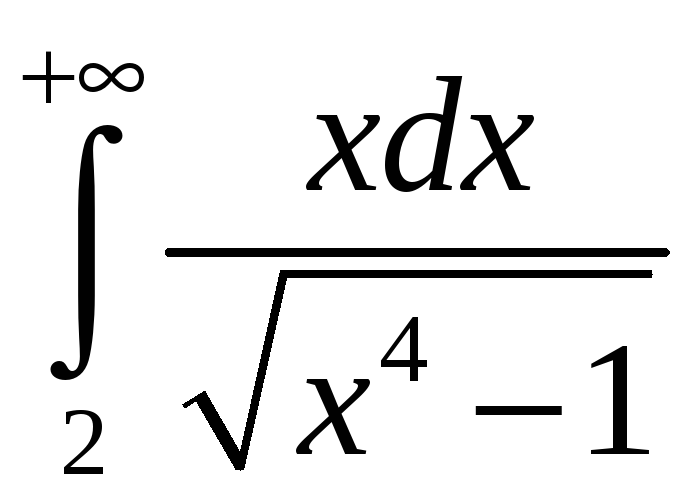 . 3.5.
. 3.5.
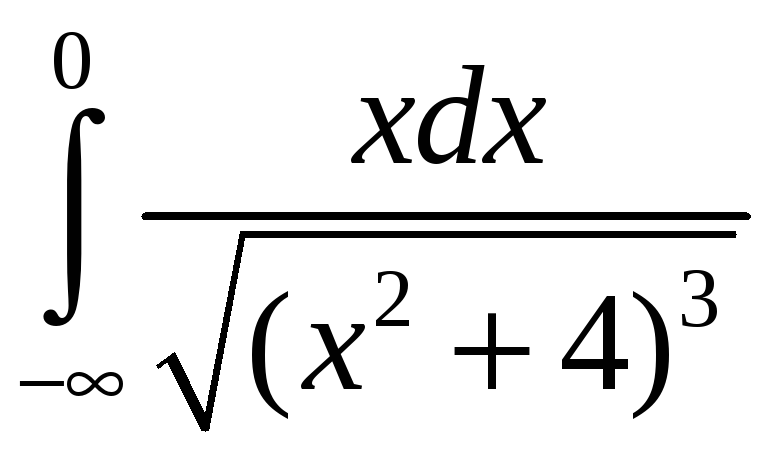 . 3.6.
. 3.6.
 .
.
3.7.
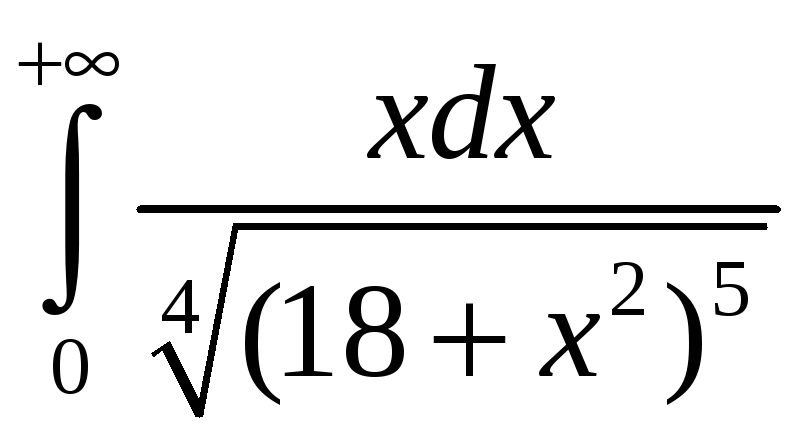 . 3.8.
. 3.8.
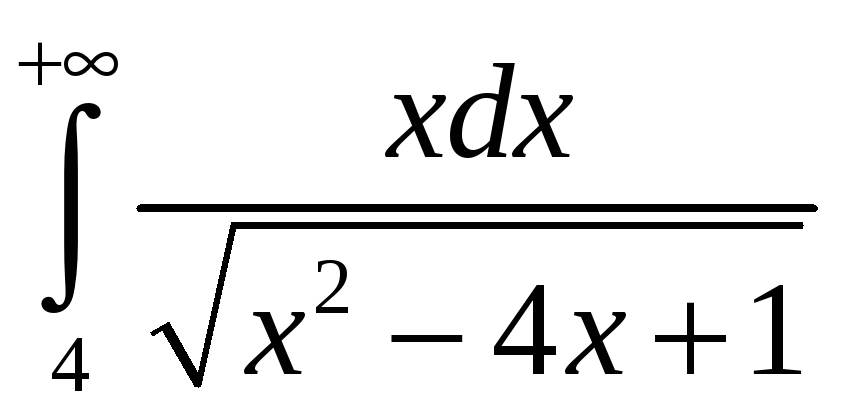 . 3.9.
. 3.9.
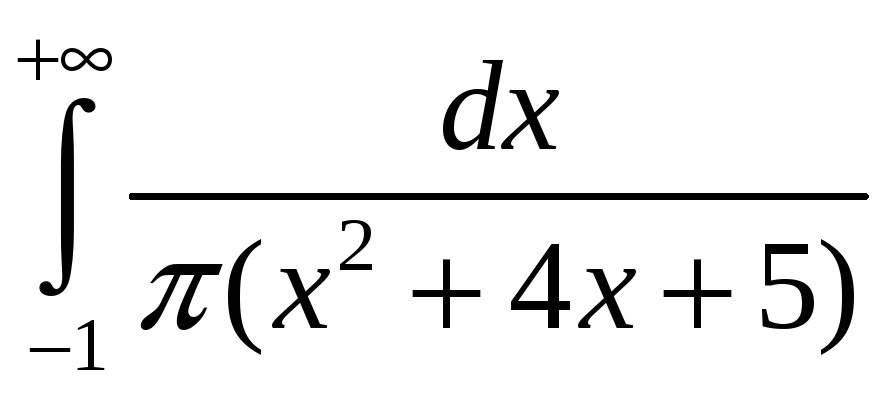 .
.
3.10.
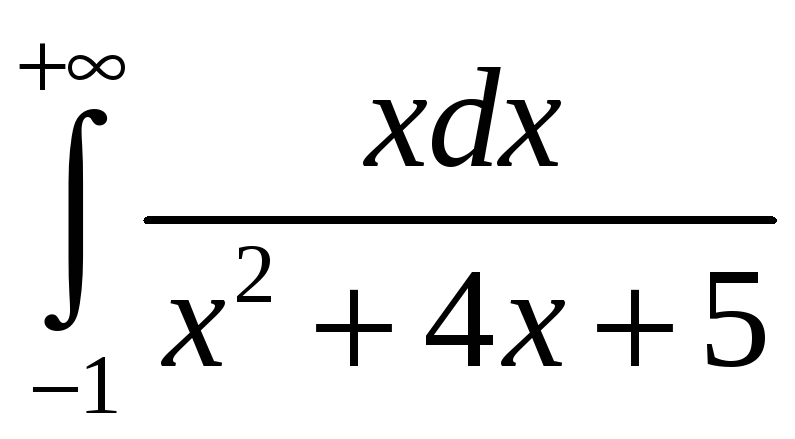 . 3.11.
. 3.11.
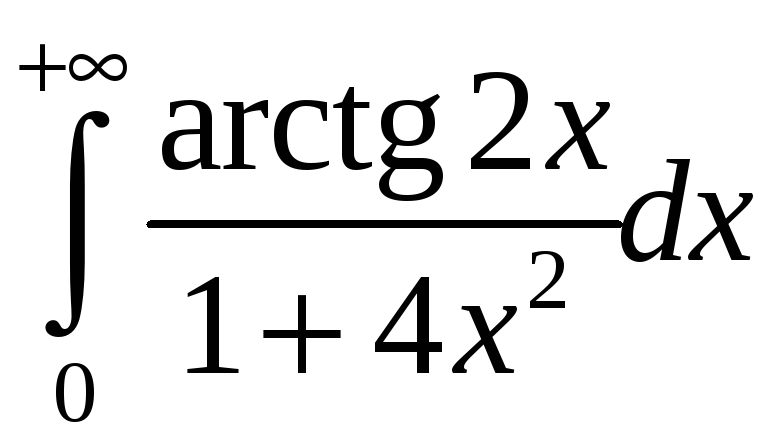 . 3.12.
. 3.12.
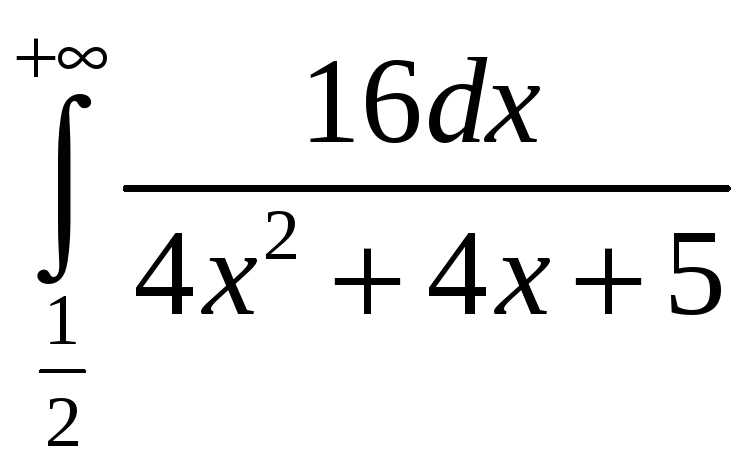 .
.
3.13.
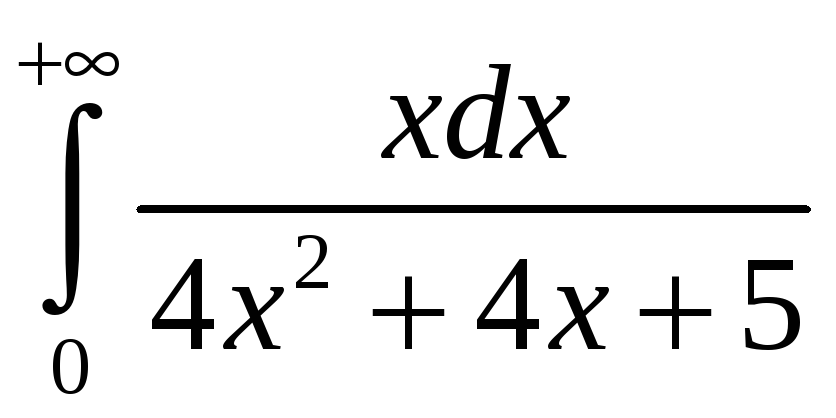 . 3.14.
. 3.14.
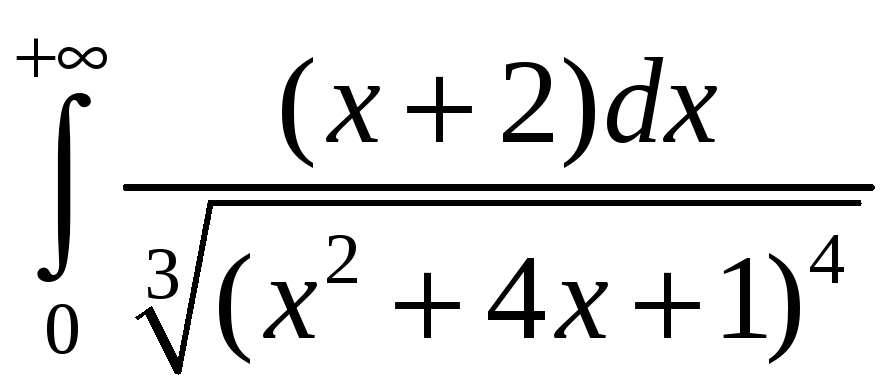 . 3.15.
. 3.15.
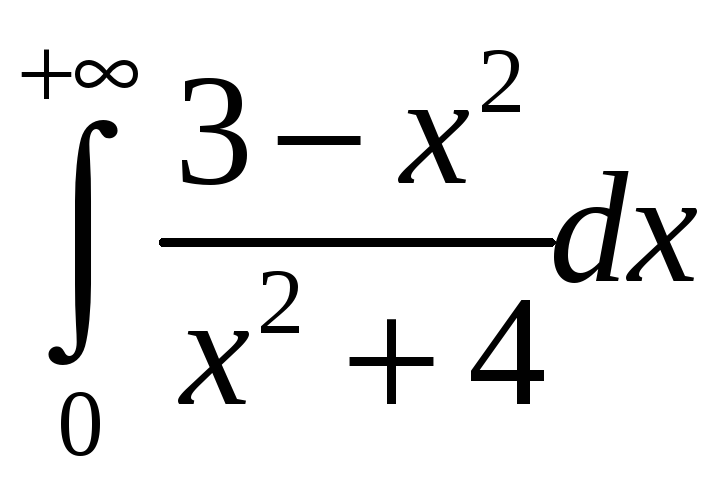 .
.
3.16.
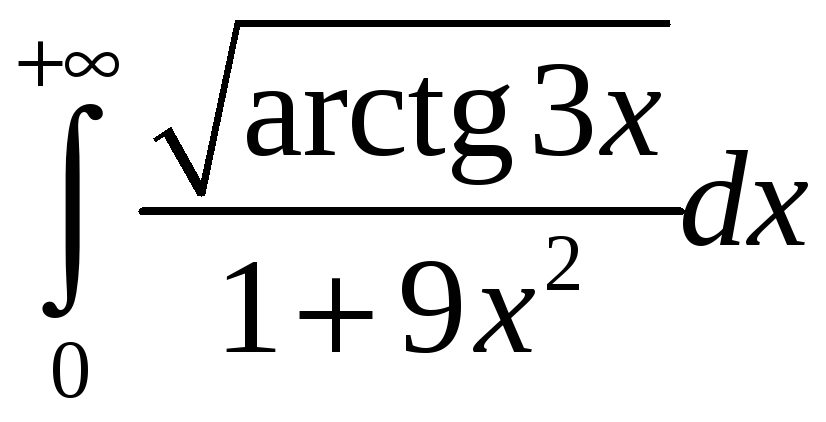 . 3.17.
. 3.17.
 . 3.18.
. 3.18.
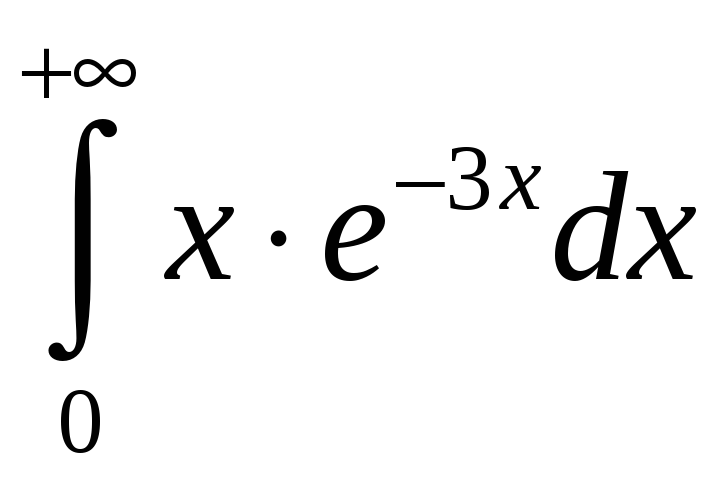 .
.
3.19.
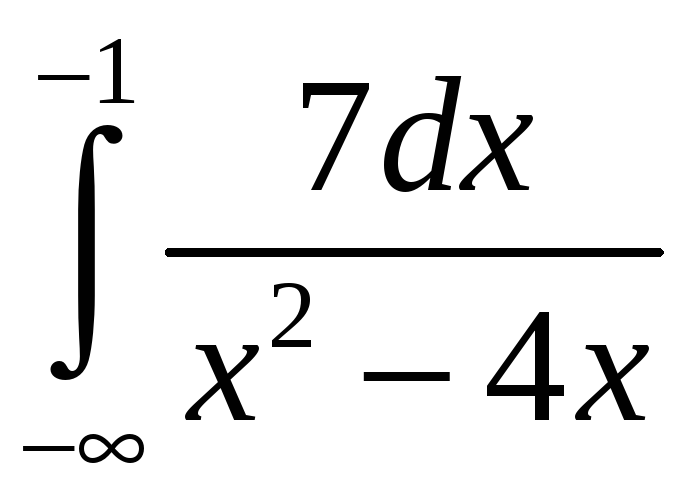 . 3.20.
. 3.20.
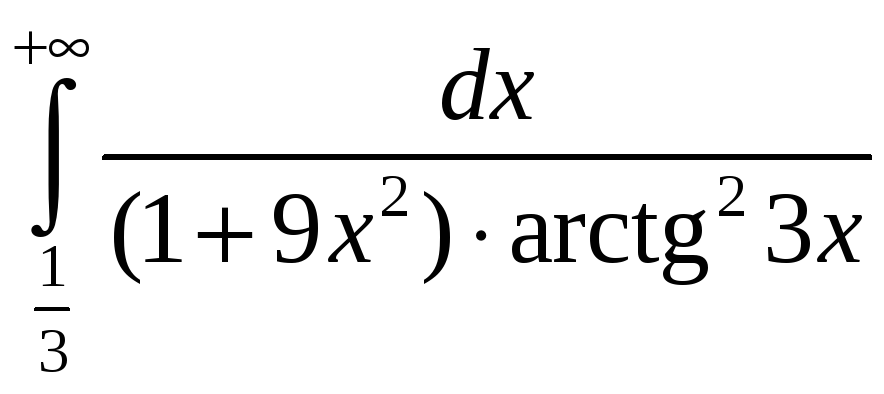 . 3.21.
. 3.21.
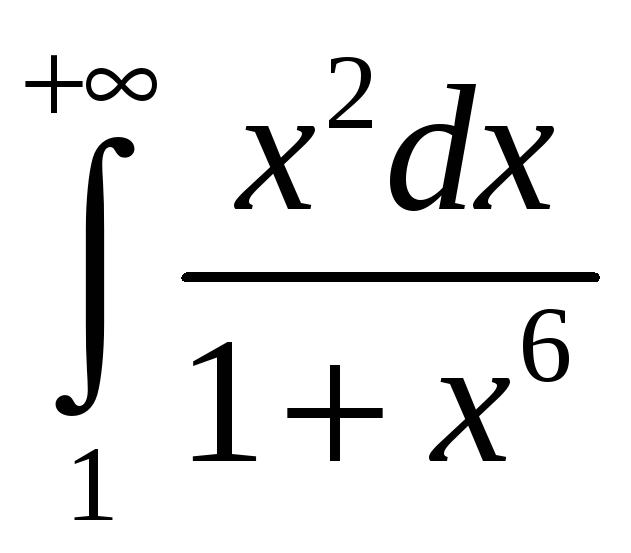 .
.
3.22.
 . 3.23.
. 3.23.
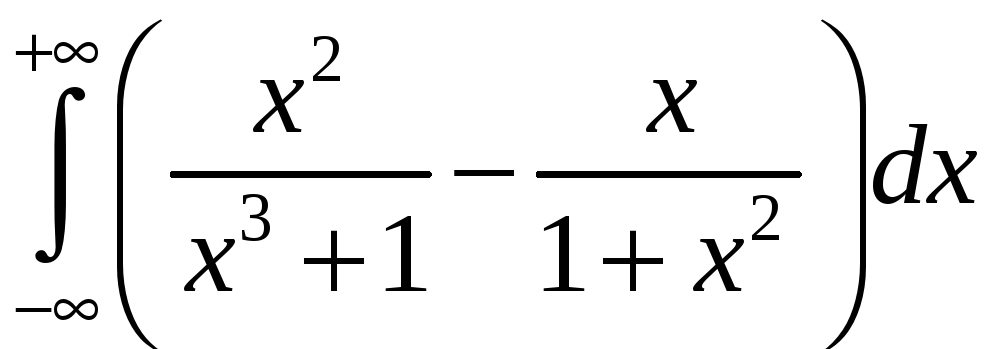 . 3.24.
. 3.24.
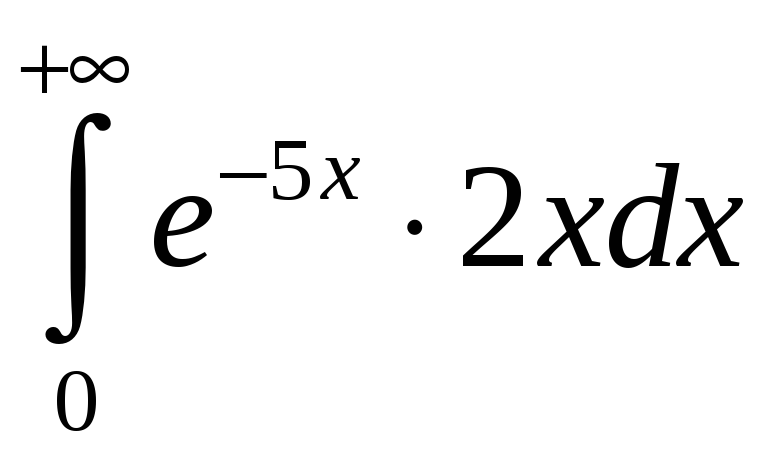 .
.
3.25.
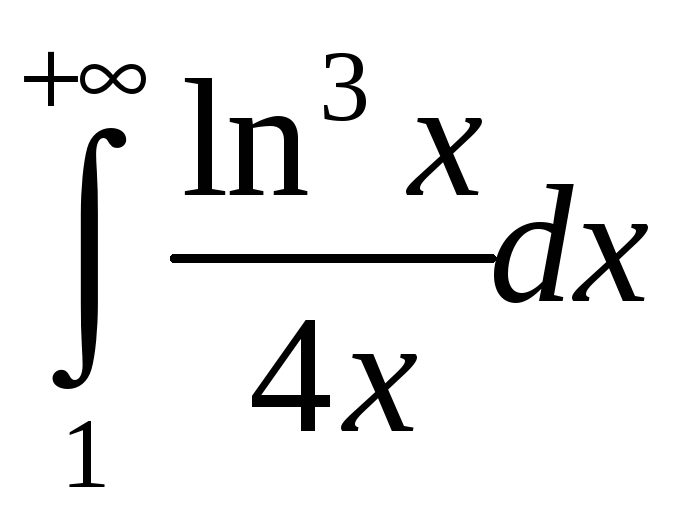 . 3.26.
. 3.26.
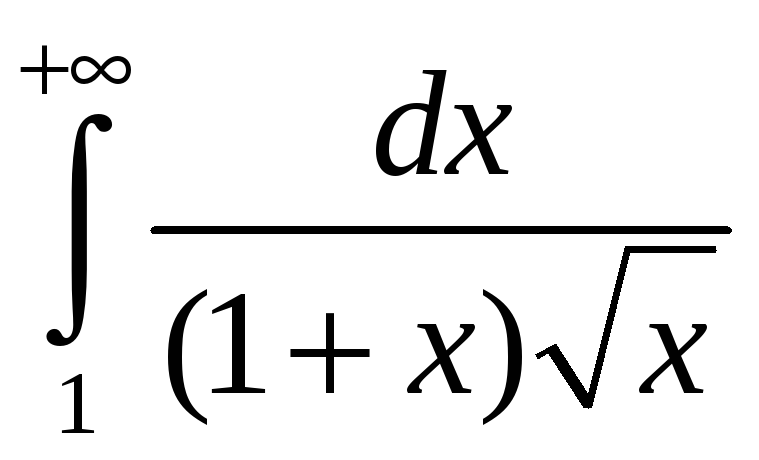 . 3.27.
. 3.27.
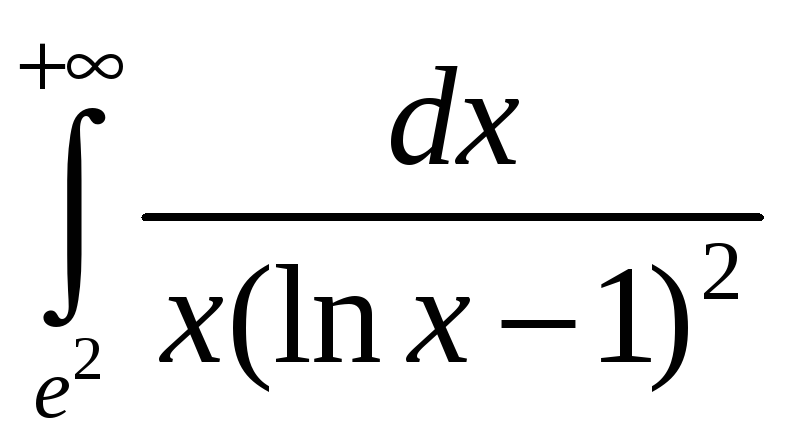 .
.
3.28.
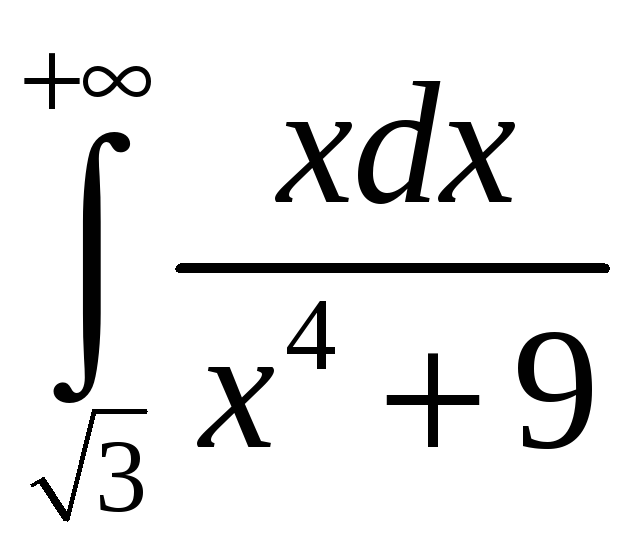 . 3.29.
. 3.29.
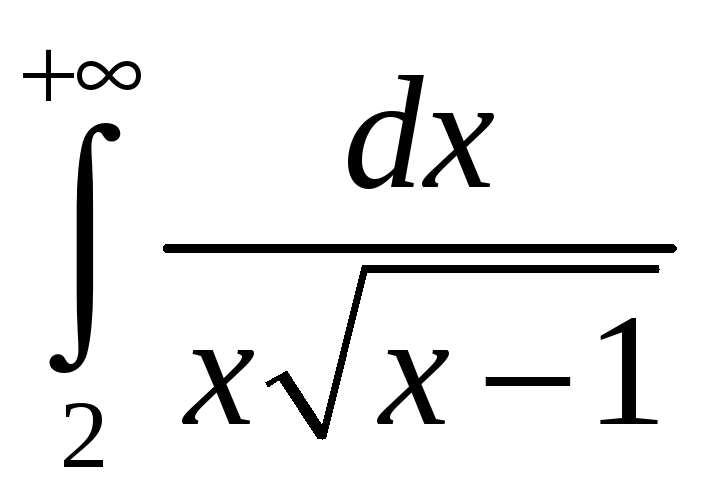 . 3.30.
. 3.30.
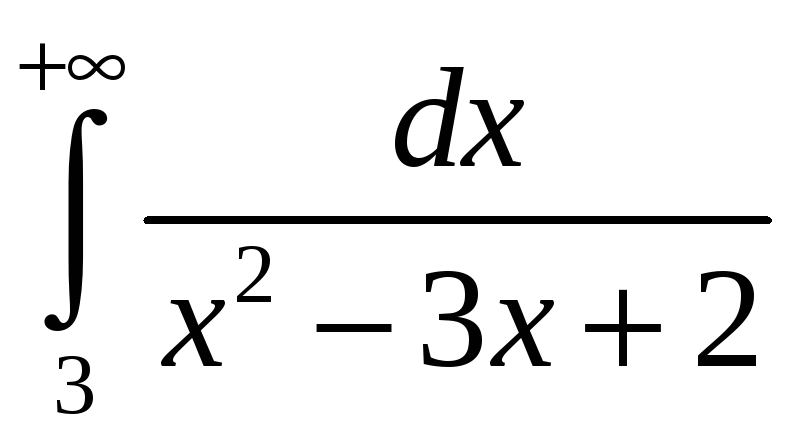 .
.
Тема 4. Двойной интеграл
Пусть функция
![]() определена в ограниченной замкнутой
области
определена в ограниченной замкнутой
области
![]() плоскости
плоскости
![]() .
Разобьем область
.
Разобьем область
![]() произвольным образом на
произвольным образом на
![]() элементарных областей
элементарных областей
![]() ,
имеющих площади
,
имеющих площади
![]() и диаметры
и диаметры
![]() (диаметром области называется наибольшее
из расстояний между двумя точками
границы этой области). Выберем в каждой
элементарной области
(диаметром области называется наибольшее
из расстояний между двумя точками
границы этой области). Выберем в каждой
элементарной области
![]() произвольную точку
произвольную точку
![]() .
.
Интегральной
суммой для
функции
![]() по области
по области
![]() называется сумма вида
называется сумма вида
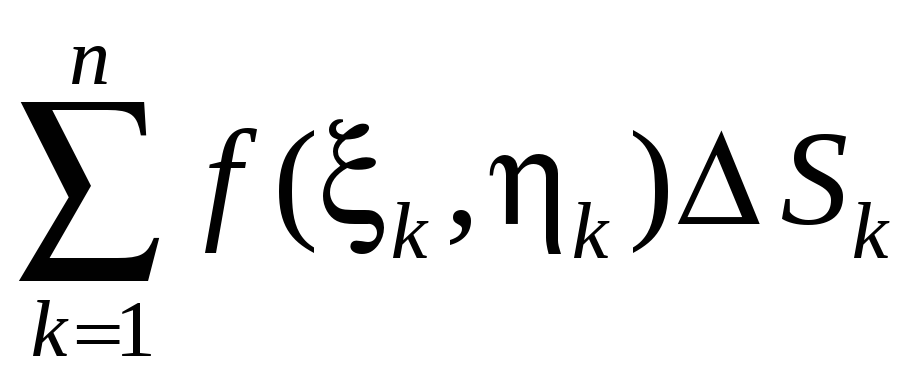 .
.
Если при
![]() интегральная сумма имеет определенный
конечный предел
интегральная сумма имеет определенный
конечный предел
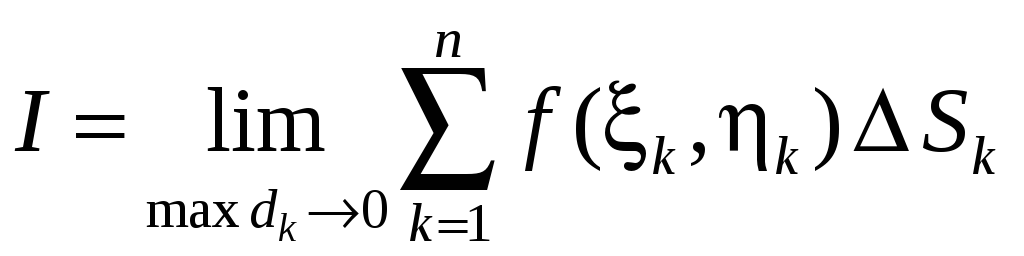 ,
не зависящий от способа разбиения
,
не зависящий от способа разбиения
![]() на элементарные области и от выбора
точек
на элементарные области и от выбора
точек
![]() в пределах каждой из них, то этот предел
называется двойным
интегралом от
функции
в пределах каждой из них, то этот предел
называется двойным
интегралом от
функции
![]() в области
в области
![]() и обозначается следующим образом:
и обозначается следующим образом:
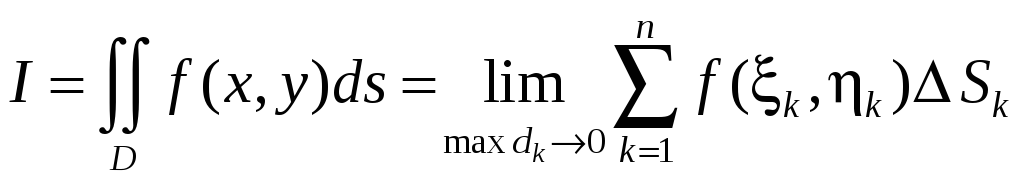 .
.
Если
![]() в области
в области
![]() ,
то двойной интеграл
,
то двойной интеграл
![]() равен объему
цилиндрического тела,
ограниченного сверху поверхностью
равен объему
цилиндрического тела,
ограниченного сверху поверхностью
![]() ,
сбоку цилиндрической поверхностью с
образующими, параллельными оси
,
сбоку цилиндрической поверхностью с
образующими, параллельными оси
![]() ,
и снизу областью
,
и снизу областью
![]() ,
принадлежащей плоскости
,
принадлежащей плоскости
![]() .
.
