3. Теория алгоритмов и рекурсивных функций

Мы начнем с интуитивно ясного понятия алгоритма.

Алгоритм есть метод решения некоторой задачи с входными данными. Этот метод может быть разложен на отдельные единичные шаги, исполне­ние которых и порядок их следования однозначно определены. Этот метод должен иметь возможность описания с помощью текста конечной длины. При этом «решение проблемы с одним входом» есть, в сущности, вычис­ление значения функции для заданного аргумента.

Для того чтобы математически овладеть понятием алгоритма, следует заменить его формализованным понятием, а именно его экспликатом, т.е. интерпретацией. Существуют различные интерпретации понятия алго­ритма, такие, как μ-рекурсивные функции, машины Тьюринга, грамматики типа 0, грамматики Ван-Вайнгаардена и др. При этом эти интерпретации служат также для описания алгоритмов, что означает: каждая конкретная μ-рекурсивная функция, каждая конкретная машина Тьюринга, каждая конкретная грамматика типа 0, каждая конкретная грамматика Ван-Вайн­гаардена описывает определенный алгоритм; она, таким образом, репре­зентирует алгоритм. Мы в дальнейшем не будем делать строгого различия между конкретным алгоритмом и его возможными описаниями (если это не приведет к неясности). Все эти интерпретации эквивалентны в том смысле, что каждый алгоритм, который может быть описан с помощью одной из этих интерпретаций, таким же образом может быть описан и с помощью любой другой из этих интерпретаций. Также и любой формально определенный язык программирования с определенными минимальными требованиями (как, например, присваивание и структура циклов) может рассматриваться как интерпретация понятия алгоритма. В это число попа­дают все имеющиеся языки программирования (машинный код, Ассемб­лер, Бейсик, Алгол 60, Алгол 68, Фортран, Паскаль, Модула-2, Лисп, …).

Мы рассмотрим сначала такие алгоритмы, отдельные шаги которых со­стоят в изменении слов над заданным алфавитом. Если достигается конец этого процесса изменения, то полученное слово есть результат алгоритма при некотором определенном входе. Если же при некотором определенном входе конец этого процесса изменения не достигается, то результат не оп­ределен.

Мы будем полагать теперь, что понятие алгоритма формально опреде­лено, а именно с помощью одной из приведенных интерпретаций. (Для дальнейшего достаточно выбрать некоторый язык программирования и описать алгоритмы с помощью программ на этом языке.) Мы хотим далее с помощью понятия алгоритма получить другие понятия и рассмотреть ос­новы теории рекурсивных функций.

Пусть М – бесконечное множество, тогда М является эффективно ну­мерованным (счетным) с помощью биективной функции F:М тогда и только тогда, когда для всех входных данных из  найдется алгоритм, с по­мощью которого для любого п может быть эффективно вычислено значе­ние обратной к F функции в точке п, т.е. F ^-1(п)  М. В случае, если М конеч­но, где М= п, то в этом определении  следует заменить на {0,1,..., п-1}.

Таким образом, можно говорить об n-м элементе F ^-1(п) множества М. Если обозначить F ^-1(п) через x_n, то последовательность

x₀, х₁,…, х_n,…

является эффективной нумерацией множества М. Элемент хМ имеет то­гда индекс F(х) . Также говорят, что F кодирует М, F ^-1 декодирует М.

Пример 3.1. (1) Пусть ={a₁,...,a_k  – алфавит. Лексикографический по­рядок над ^*определяется следующим образом:

Пусть w₁, w₂ ^*. Тогда w₁  w₂ 

(i)  w ₁   w ₂, или

(ii)  w ₁   w ₂, w₁  va_i v₁, w₂  va_j v₂, ij, v, v₁, v₂  ^*, или

(iii) w ₁  w ₂

Порядок  является полным и нётеровым и ^* может быть эффективно занумеровано согласно лексикографическому порядку. Иногда также сле­дующий порядок называется лексикографическим:

w ₁ ’ w ₂ 

(i) w₂  w₁v, v^*, или

(ii) w₁  va_i v₁, w₂  va_j v₂, ij, v, v₁, v₂  ^*.

Этот порядок  ’ полный, но не нётеров:

a₂ >’ а₁ а₂>’ a₁ a₁ a₂ >’…’ a a₂’…

В лексике применяется этот лексикографический порядок.

(2) Пусть М=, М_п – конечно, причем |М_n|=k_n, k_n>0, М_iМ_j= для ij. Пусть М_n эффективно нумеровано посредством функции F_n М_п  {0,1,…, k_n-1}, тогда последовательность

F(0),..., F (k₀ – 1), F (0),..., F (k₁ – 1),..., F (0),..., F (k_n – 1),...

является эффективной нумерацией множества М.

(3) Множество D₁×D₂, где D₁ и D₂ являются эффективно счетными, само является эффективно счетным. Пусть D_i эффективно нумеруется посредст­вом G_i: D_i, i 1,2.

Определим для п  0,

М_n = {(d₁,d₂)| G₁ (d₁)+ G₂(d₂)  n, d₁ D₁, d₂ D₂}

и

F_n ((d₁,d₂)) = G₁ (d₁)  n – G₂(d₂), (d₁,d₂)  М_n.

Тогда, согласно (2), последовательность

(G(0),G(0)), (G(0),G(1)), (G(1),G(0)),(G(0),G(2)),…

является эффективной нумерацией D₁×D₂. Oна называется диагональной нумерацией. 

В дальнейшем, пусть Е и D – эффективно счетные множества. (Боль­шей частью Е = ×…×, D = ^*). Тотальная функция F: ЕD называ­ется вычислимой (а также рекурсивной), тогда и только тогда, когда существует один для всех аргументов из Е завершающийся алгоритм, с помощью которого для каждого аргумента xЕ можно эффективно вычис­лить значение функции F(x) D. Частичная функция F: ЕD называется частично вычислимой (а также частично рекурсивной) тогда и только то­гда, когда существует алгоритм, который обеспечивает следующее. Если F(x), xЕ, определено, то алгоритм завершается при вводе х и возвращает F(x) D); если F(x), xЕ, не определено, то при вводе х алгоритм не за­вершается за конечное время.

Тем самым понятия «алгоритм» и «частично вычислимая функция» со­ответствуют друг другу в следующем смысле: каждый алгоритм опреде­ляет частично вычислимую функцию, которая посредством него вычисля­ется.

Полагая в предыдущих определениях E ×…×, D=, получают чи­словые вычислимые и соответственно частично вычислимые функции. В сущности, можно ограничиться числовыми функциями : . Именно пусть G: ЕD вычислимая (соответственно частично вычислимая) функ­ция. Тогда существуют биективные функции F₁: Е и F₂  D, такие, что Е посредством F₁ и D посредством F₂ – эффективно счетные. Пусть :  – функция, определяемая посредством:

(n) = F₂(G (F (n))), п .

Очевидно, является вычислимой (соответственно частично вычисли­мой) и выполняется: G(x)=F( (F₁(x))), х  Е. Действительно, из определе­ния следует: F( (n)) = G (F (n)). Положим теперь х= F(n), тогда п = F₁(x) и F( (F₁(x)))=G(x).

Множество М  D называется рекурсивно перечислимым тогда и только тогда, когда существует вычислимая функция F  ЕD, с подходящим об­разом выбранным множеством Е, такая, что область значений функции F совпадает с М, т.е., М={F(x)  хЕ} или, короче, М = F(E). В дальнейшем пустое множество  также является рекурсивно перечислимым.

Название «перечислимое» множество отражает следующую сущность: Пусть z₀, z₁,…,z_n, …– эффективная нумерация Е. Тогда M может быть пе­речислено посредством

F(z₀), F(z₁), …, F(z_n), …

Множество М  D называется рекурсивно разрешимым (или рекурсив­ным), если М и D – М рекурсивно перечислимы.

Так как оказывается, что введенные уже перечислимые и разрешимые формальные языки являются в точности рекурсивно перечислимыми и ре­курсивно разрешимыми формальными языками, то в дальнейшем мы бу­дем, если это не приведет к неясностям, слово «рекурсивный» опускать.

Пусть М  D. Определим тогда характеристическую функцию ^_M D {0,1} множества М (относительно D) посредством:

^_M (x)  _.

Тогда справедливо, что M  D разрешимо тогда и только тогда, когда ^_M вычислима. Это может быть показано следующим образом:

Для М =  или М = D, М является разрешимым ( перечислимо по оп­ределению и D – перечислимо посредством тождественной функции, кото­рая, конечно, вычислима). Далее, в этих случаях выполняется, что характе­ристическая функция ^_M является вычислимой (так как она в случае М =  всегда принимает значение 0 и в случае М=D всегда значение 1). Теперь рассмотрим случай М  и М D.

(i) Пусть ^_M – вычислимая. Пусть М и  D–М произвольные, но фиксированные элементы. Мы определим две функции F₀,F₁:DD как

F₀(x) = ; F₁(x)=

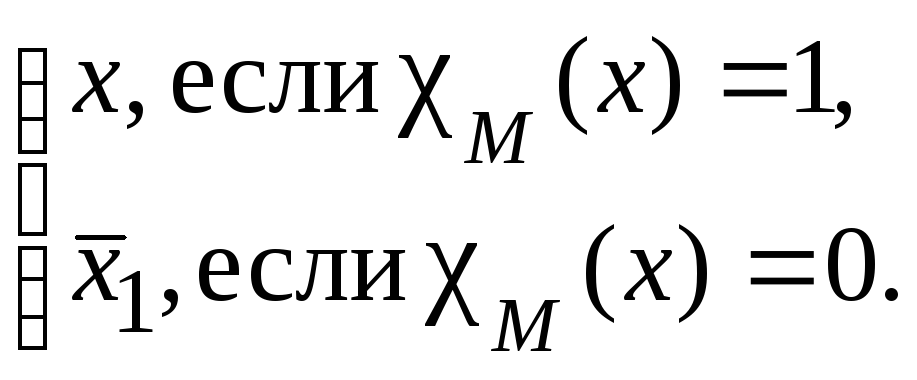
Конечно, F₀ и F₁ являются вычислимыми и выполняется: F₀(D)=D–М и F₁(D)= М. Отсюда D–М и М перечислимы и М – разрешимо.

(ii) Пусть М – разрешимо. Тогда М и D–М – перечислимы. Поскольку М   и М  D, то существуют две вычислимые функции F₀ и F₁, которые перечисляют множества D–М и М:

D –M  у₀, у₁, …,у_n,…,      

M  x₀, x₁,…,x_n,….

Мы хотим теперь для z_D вычислить значение ^_M (z). Для этого при­меним следующий алгоритм: для каждого i = 0, 1,2... вычислим с помощью F₀ и F₁ элементы y_i и х_i. А так как z должен встретиться или в последова­тельности (у_n), или в последовательности (x_п), то существует такое т, что выполнимо z = у_т или z = x_m. В первом случае мы положим ^_M (z) = 0, а во втором случае положим ^_M (z)=1. Тем самым характеристическая функция ^_M – вычислимая.

Подобное выполняется и для перечислимых множеств. Пусть МD. Мы определим частичную характеристическую функцию:D{1} множе­ства М (относительно D) посредством

(x)

Тогда справедливо, что М  D перечислимо тогда и только тогда, когда – частично вычислимая. Это может быть показано следующим образом:

(i) Пусть – частично вычислимая. В случае, если (x) является не определенной для всех x D, тогда М =  и поэтому является перечис­лимым множеством.

Пусть теперь ()=1 для D. Тогда выполняется М. Определим функцию F: ( – {0})×D D посредством

F((n,x))=

Так как ( – {0})×D, согласно примеру 3.1(3), является эффективно счетным, то функция F – вычислимая. А вследствие М={F((n,x))  п1, xD}, М является перечислимым.

(ii) Пусть М – перечислимое. Для М =  функция нигде не опреде­лена и поэтому частично вычислимая. Для М   существует вычислимая функция F:ЕD, которая перечисляет М:

M: x₀, x₁, …,x_n, …

Мы хотим теперь для элемента zD вычислить значение (z). Для этого сравним последовательно z с х_i, i  0. Если мы найдем т0, для кото­рого z = x_т, то положим (z)  1. В противном случае (z) не опреде­лена.

Из-за этих обстоятельств перечислимые множества называют также по­луразрешимыми множествами. Таким образом, справедливо, что множе­ство М  D разрешимо тогда и только тогда, когда М и D–М полуразре­шимы.

Определим теперь важный экспликат понятия частично вычислимой функции, а именно -рекурсивные функции. Эти функции отображают (^*)ⁿ, п (п-кратное декартово произведение множеств ^*) в ^*. Сначала определим три вида простых базовых функций:

(i) Для любого а отображение N_a: ^* ^*, N_a(w) = wa, w  ^*, называ­ется функцией следования.

(ii) Для любого п  0 отображение Сⁿ:(^*)ⁿ^*, Сⁿ(w₁,w₂,...,w_n)=, w_i^*, 1 i n, называется п-местной нуль-функцией.

(iii) Для любого п  1 и 1jп отображение :(^*)ⁿ  ^*, (w₁,w₂,...,w_n)=w_j, w_i ^*, 1i n называется п-местной проекцией.

Определим далее три функционала, которые позволяют получить но­вые функции из уже ранее определенных функций.

(i) Пусть п  0, т  1 и H: (^*)^m^*, G_j: (^*)ⁿ ^*, 1jm. Функция F: (^*)ⁿ  ^* образуется из Н путем подстановки функций G ₁, G₂,…, G_m тогда и только тогда, когда для всех w_i^*, 1i п, выполняется:

F (w₁, w₂,..., w_n) = Н (G₁ (w₁,..., w_n),...,G_m (w₁,..., w_n)).

(ii) Пусть n  1, G: (^*)^n-1^* и Н_а: (^*)ⁿ⁺¹ ^*, a. Функция F:(^*)ⁿ^* образуется из G и H_a, a, посредством рекурсии тогда и только тогда, когда для всех w_i^*,1 i n, имеет место

F(,w₂,…,w_n)  G(w₂,…,w_n), F(w₁a,…,w_n)  H_a(F(w₁,…,w_n),w₁,…,w_n), a.

(iii) Пусть n  0 и G: (^*)ⁿ⁺¹^*. Функция F: (^*)ⁿ^*образуется из G пу­тем минимизации относительно a тогда и только тогда, когда для всех w_i ^*, 1 i  п выполняется:

F(w₁,…,w_n)  _a G (w₀,w₁,…,w_n).

При этом _а G (w₀,w₁,…,w_n)] определена следующим образом: в слу­чае, если найдется некоторое т0, такое, что G (а^l, w₁,..., w_n), 0lm, опре­делена, причем G(а^l,w₁,..., w_n), 0l<m и G(а^m,w₁,...,w_n)=, то выполняется: _а [G (w₀, w₁,..., w_n)] = a^m. В противном случае _а [G (w₀, w₁,..., w_n)] не опре­делена.

С помощью базовых функций и функционалов определяют примитивно рекурсивные и -рекурсивные функции. Семейство примитивно рекурсив­ных (соответственно -рекурсивных) функций над  есть наименьшее се­мейство функций F:(^*)ⁿ^*, n, которое содержит _a, а, C⁰, , n1, и замкнуто относительно подстановки и рекурсии (соответственно подста­новки, рекурсии и минимизации).

Ясно, что -рекурсивная функция в общем случае является частично рекурсивной, тогда как примитивно рекурсивная функция всегда вполне ‑рекурсивна.

Из приведенных выше определений получают числовые функции из ⁿ в , полагая, что  одноэлементный алфавит, ={а}, и идентифицируя a^m с числом т. В частности, числу 0 соответствует элемент . Семейство чи­словых примитивно рекурсивных функций (соответственно числовых - ре­курсивных функций) есть наименьшее семейство функций F: ⁿ , n  0, которое содержит N (=N_a), С^, , n 1 и замкнуто относительно подста­новки и рекурсии (соответственно подстановки, рекурсии и минимизации).

Для того чтобы получить компактное описание -рекурсивных функ­ций над , введем -рекурсивные программы. Каждая -рекурсивная про­грамма имеет один или несколько входов в зависимости от того, на какое количество аргументов из ^* она рассчитана. Каждая п-местная ‑рекурсивная программа представляет п-местную -рекурсивную функ­цию (служит для вычисления этой функции). Выберем (всюду, где это возможно) следующие обозначения: -рекурсивная функция будет обозна­чаться большими буквами, -рекурсивная программа, которая ее вычис­ляет, будет обозначаться теми же самыми малыми жирными буквами. Пусть ={a ₁,..., a _k}.

(i) Программа n – одноместная и представляет функцию следования N, 1 i  k.

(ii) Программа c – нуль-местная и представляет нуль-функцию С⁰.

(iii) Программа u может иметь любое число входов п  1 и представляет .

(iv) Пусть -рекурсивные функции Н: (^*)^m ^* и G_j: (^* ⁿ, ljn, n  0, m  1 представляются через т-местные (соответственно, п-местные) программы h и g_j. Функция F, которая образуется путем подстановки G₁,...,G_m в Н, представляется п-местной программой h (g₁,..., g_m).

(v) Пусть -рекурсивные функции G(^*)^n-1 ^* и Н:(^* ⁿ⁺¹ ^*, 1ik, n  1 представлены через (n – 1)-местные (соответственно (n+1)-мест­ные) программы g и h. Функция F, которая образуется путем рекур­сии из G и Н, 1 i k, представляется n-местной программой [gh,..., h].

(vi) Пусть -рекурсивная функция G: (^*)ⁿ⁺¹^*, n 1 представлена (n+1)‑местной программой g. Функция F, которая образуется из G пу­тем минимизации относительно a_i, 1i k, представляется n-местной программой g.

Синтаксис языка -рекурсивных программ (без учета разрядности), таким образом, задан следующими продукциями:

Pn…n c  u  P(L) [P^k+1  P… P, L PL  P

-рекурсивная программа, в которой не встречаются символы , , называ­ется примитивно рекурсивной программой. В случае числовых ‑рекур­сивных программ k = 1 и индексы при n и  опускаются:

Pn  c  u  P(L)  [PP  P.

Пример 3.2. (1) Мы хотим функции , п  2, 2jn представить с помо­щью программ. Пусть u_j – программа произвольной размерности большей или равной j, такая, что примененная к (w₁,...,w_n), где n j, воз­вращает слово w_j (u₁= u). Тогда [u_j u^k] есть программа размерности  j+1, такая, что примененная к (w₁,..., w_n), где n  j+1, возвращает слово w_j+1. По­этому [u_j u^k] представляет следующую функцию F:

F (, w₂, …,w_n) = (w₂, …, w_n),

F (w₁a,w₂,…,w_n) = (F (w₁,w₂,…,w_n), w₁,w₂,...,w_n), a.

Тем самым выполнено:

F (w₁a, w₂,…, w_n) =... =F (, w₂,..., w_n) = (w₂,..., w_n)= w_j+1.

(2) Представим Сⁿ,п0 с помощью п-местной программы c_n. Функция Сⁿ представляется с помощью [c_n-1 u^k ] (где c₀ = c). Тогда c_n-1u^k ] представ­ляет следующую функцию F:

F (, w₂,…, w_n) = C^n-1(w₂, …, w_n),

F (w₁a,w₂,..., w_n) = (F (w₁,w₂,...,w_n), w₁, w₂,…, w_n), a,

при этом выполняется:

F (w₁a, w₂,..., w_n) =... = F (, w₂,..., w_n) = C^n-1(w₂,..., w_n).

(3) Представим одноместную постоянную функцию K_v, v^*, где K_v(w)v, для всех w^*с помощью программы. Пусть k_v – одноместная про­грамма, которая представляет K_v. Тогда [сu^k] представляет функцию K_ = С¹ и n_a (k_v) представляет постоянную функцию K_va, a. Поэтому n_a(k_v) представляет следующую функцию F:

F (w) = N_a (K_v (w)) = N_a (v) = va.        

Теперь мы хотим определить дальнейшие функционалы, позволяющие из примитивно рекурсивных (соответственно -рекурсивных) функций снова получать того же рода функции.

Предложение 3.1. Пусть G^*ⁿ^*, H^*^m^*, H_a^*^*, a, – примитивно рекурсивные (соответственно -рекурсивные) функции. Тогда следующие функции F тоже являются примитивно рекурсивными (соот­ветственно -рекурсивными)

(i) F(w₁,…,w_n)=G(w_(1),…,w_(n)),где  – перестановка из …n.

(ii) F(w₁,…,w_l1,w_l+1,…,w_n,v₁,..,v_m)=G(w₁,…,w_l1,H(v₁,..,v_m),w_l+1,..,w_n).

(iii) F(w₁,…,w_n,)G(w₁,…,w_n),

F(w₁,…,w_n,w₀a)=H_a(F(w₁,…,w_n,w₀)),a.

Доказательство Функции G, H, H_a могут быть представлены про­граммами g, h, h_a, a.

(i) F представяется программой g(u_,…,u_n). Поэтому справедливо:

F(w₁,…,w_n)=G(Uw₁,…,w_n,…,U(w₁,…,w_n))=G(w_(1),…,w_(n)).

(ii) F представляется программой g(u₁…u_l-1h(u_n…u_n+m-1)u_l…u_n-1).

(iii) программа gh(u)…h(u)(u_n+1u₁…u_n) представляет функцию F₁. Тогда справедливо:

F₁(w₁,…,w_n,w₀)=F₂(w₀,w₁,…,w_n),

где F₂ представлятся программой gh(u)…h(u), таким образом,

F₂(, w₁,…,w_n) = G(w₁,…,w_n),

F₂(w₀a_i,w₁,…,w_n)  (F₂(w₀,w₁,…,w_n),w₀,w₁,…,w_n))=

= (F₂(w₀,w₁,…,w_n)), 1 i k.

Тем самым получим

F₁(w_1,…,w_n, )  G(w₁,…,w_n),

F₁(w₁,…,w_n,w₀a) = (F(w₁,…,w_n,w₀)), 1 i k

и F₁ совпадает с F. 

Пример 3.3. (1) Мы хотим записать программу con₂ для функции CON₂^*×^*^* с CON₂w₁,w₂w₁w₂ Справедливо:

CON₂w_1,    U(w),

CON₂w₁,w₂a  N_a(CON₂w₁,w₂), a.

Согласно предложению 3.1 (iii) CON₂ является примитивно рекурсивной и con₂u n(u)… n(u) u₂ u .

(2) Программа con_n для n-местной функции CON_n, n  , с CON_nw₁,…,w_n w₁,…,w_n имеет вид: con₂ con_n-1 u₁…u_n-1u_n. 

Пример 3.4. Мы хотим представить теперь некоторые числовые функ­ции программами. Все x,y лежат в .

(1) Функция следования.

Пусть N_t  , t1, – функция N_t(x)x+t, таким образом, N₁(x)N(x) и N_t+1(x)N(N_t(x)).

n₁n, n_t+1n(n_t), t 1.

(2) Константа.

Пусть K ⁿ – n-местная постоянная функция, причем K(x₁,…,x_n)i.

а) Нульместная константа.

kc, kn_i(c).

b) Одноместная константа. K=C^0, K(x+1)=U(K(x),x).

k=c u, k=(n_i k).

c) n-местная константа, n2. K(x₁,…,x_n)=K((x₁,…,x_n)).

k₀=k (u), k _i=n_i (k₀).

(3) Сумма.

SUM(0, y) = y = U(y),

SUM(x+1,y)=SUM(x,y)+1=N(SUM(x,y))=N(U(SUM(x,y)),x,y).

sum= un(u).

(4) Произведение.

PROD(0, y)=0= K(y),

PROD(x+1,y)=SUM(PROD(x,y),y) =

=SUM(U(PROD(x,y),x,y),U(PROD(x,y),x,y)).

prod =ksum(u u₃) =  cuunuu u uu)].

(5) Потенцирование.

EXP(0, y) = 1 = K(y),

EXP(x+1,y) = PROD(EXP(x,y),y)=

=PROD(U(EXP(x,y),x,y),U(EXP(x,y),x,y).

exp=kproduu₃ncucuunuuuuuuuuu

(6) Функция предшествования.

V(0) = 0 = C⁰,

V(x+1) = x = U(V(x),x).

v = c u₂   cu u .

(7) Разность.

DIFF1(0, y) = y = U(y),

DIFF1(x+1,y) =V(DIFF1(x,y)) = V(U(DIFF1(x,y),x,y)

DIFF(x, y) = DIFF1(y,x) = DIFF1(U(x,y),U(x,y).

diff1=uvu = ucuu(u), diff = ucuu uuuu.

(8) Факториал.

FAK(0) = 1 = K,

FAK(x+1) = PROD(FAK(x),N(x)) =

= PROD(U(FAK(x),x),N(U(FAK(x),x))).

fak = kprodunu₂=nccuunuu[uuuunuu.

(9) Знак.

SGN(0) = 0 = C⁰,

SGN(x+1) = 1 =K(SGN(x),x).

sgn = c kcn(cu(u)).

Покажем теперь, что алфавит  а₁,…,а_k может эффективно нумеро­ваться с помощью биективной примитивно рекурсивной функции С_k. Здесь снова речь идет о лексикографическом порядке. Мы определяем С_k ^* ( отожествляется с а) через

С_k (   С_k(а,…,а)  i_j k^n-j.

Функция С_k отображает биективно ⁿ на числа между k ^n-1+k^n-2+…+k+1 и kⁿ +k^n-1+…+k²+k, n  1. Вследствие того, что

i_j k^n-j = k i_j k ^n-1-j+i_n,

справедливо:

C_k() = 0 = C⁰,

C_k(wa_i) = SUM(PROD(C_k(w),k) i) = N_i(P_k(U(C_k(w),w))),1ik,

где P_k(w) = PROD(U(w),K(w)).

Это дает в итоге примитивно рекурсивную программу

c _k  c n₁ p_k u…n_kp_k u  p _kprod u n_k  cu 

Обратно, можно показать, что имеется биективная примитивно рекурсив­ная функция D_k  ^*^* (в действительности D_k  ^*) с D_k(C_k(w)) = w, w^*. Тем самым мы доказали следующее предложение.

Предложение 3.2. ^* эффективно нумеруется с помощью C_k. 

Покажем теперь, что ^n, n  2, эффективно счетно. Докажем это сначала для n = 2.

Биективная примитивно рекурсивная функция   ² называется парной функцией тогда и только тогда, когда она является строго монотонной по каждому аргументу, т.е.: х₁ х₂  х₁+1 х₂ и х₁ х₂  х₁ х₂ +1 справедливо для всех х_ х_  .

Из условия монотонности следует, что х_ х_  х_ х_. Мы покажем сначала, что х_  х₁ 0. Вследствие 00   справедливо 000 и из х_  х₁ 0 следует х_  х₁+1 0 , таким образом, х_ х₁+1 0 . Из х_  х₁ 0 сразу следует х₁  х_ х_ для всех х₂. Аналогично проводится доказательство для второго аргумента.

Благодаря биективности  имеются две биективные функции __ , _х₁, х₂  х₁ и _х_ х_   х_. Из этого следует ₁х),_ (х = х, потому что для каждого х однозначно найдутся х_ х_, та­кие,что х = х_ х_. Поэтому справедливо:

₁х), _(х_х₁,х₂, _х_ х_) =  х_ х_  = х.

Для данного х, ₁х) и _(х можно охарактеризовать следующим образом: х_  ₁х)  х, х₂  ₂х)  х определены однозначно тем, что справедливо: х_ х_ = х. Ограничение ₁х)  х, ₂х)  х (конечный поиск) дает в результате, что ₁ и ₂ – примитивно рекурсивные.

Следующие функции используются часто как парные функции:

(1) ху (х+у+1)(х+у)+х (диагональная нумерация):

x y	0	1	2	3	4
0	0	1	3	6	10
1	2	4	7	11
2	5	8	12
3	9	13
4	14

_(z) = z  ,

₂(z)  – _(z).

(2)   х у  = 2^х (2у +1) –1.

Предложение 3.3. Парные функции существуют. ^ с помощью некото­рой парной функции эффективно нумеруется. 

Концепцию парной функции можно обобщить на ^n, n  2. Пусть _ – парная функция. Определим тогда

_n+1х₁,…,х_n+1) = _nх₁,…,х _n-1, ₂ х_n, х_n+1)), n  2.

Конечно, _n – снова биективная и примитивно рекурсивная функция. Обратные функции

_i,n+1: ¥¥, с _i,n+1 ( _n+1 х₁,…,х _n+1)) = х _i,

где 1in+1, можно определить через

_i,n+1(z) =

_1,2 = _1, _2,2 = _2.

Причем  _i,n+1 требуются только для 1  i  n+1 и n  2.

Предложение 3.4. ^n, n  2, эффективно нумеруется с помощью примитивно рекурсивной функции. 

Предложение 3.5. (^*)ⁿ, n  1, эффективно нумеруется с помощью примитивно рекурсивной функции.

Доказательство. Функция С:(^*)ⁿ, которая определяется через С(w₁,…,w_n) = _n(C_k(w₁),…,C_k(w_n)), w_i^*, дает эффективную нумерацию для n  2. Случай n =1 уже рассмотрен в предложении 3.2. 

В сущности, можно ограничиться одноместными числовыми прими­тивно рекурсивными функциями и -рекурсивными функциями. Для за­данной функции F  (^*)ⁿ^* мы определим функцию   че­рез(x) =C_k(F(D_k(_1,n(x)),…,D_k(_n,n(x)))). Тогда вместе с F функция тоже будет примитивно рекурсивной или - рекурсивной и справедливо:

F(w₁,…,w_n) = D_k ( (C(w₁,…,w_n))),

так как из w_i = D_k (_i,n (x)) следует C_k (w_i)  _i,n(x) и

C(w₁,…,w_n)  _n(C_k(w₁),…,C_k(w_n)  x.

Таким образом, справедливо: (C(w₁,…,w_n)) = C_k(F(w₁,…,w_n)), отсюда следует F(w₁,…,w_n) = D_k ((C(w₁,…,w_n))).

Функции C_k, D_k, _n, _1,n,…,_n,n являются примитивно рекурсивными и относительно «просто» строятся. Если функция F является «сложной», это выражается в «сложной» функции (но не в «сложном» кодировании).

Следующее предложение рассматривает применение предложения 3.4 и показывает, что «параллельная рекурсия» не выводит из класса примитивно рекурсивных (соотв. -рекурсивных) функций.

Предложение 3.6. Пусть n, m  1и G_i  ^n-1, H_i  ^m, 1im, – при­ми­­тивно рекурсивные (соотв. -рекурсивные). Тогда функции F_iⁿ, 1im,

где F_i (0, x₂,…,x_n) = G_i(x₂,…,x_n),

F_i (x₁+1, x₂,…,x_n) = H_i (F₁ (x₁,x₂,…,x_n),…,F_m(x₁,x₂,…,x_n)),

тоже являются примитивно рекурсивными (соотв. -рекурсивными).

Доказательство. С помощью примитивно рекурсивной (соотв. ‑ре­курсивной) функции

H(y₁,…,y_m) = _m(H₁(y₁,…,y_m),…,H_m(y₁,…,y_m))

мы определяем примитивно рекурсивную (соотв. -рекурсивную) функ­цию F  ⁿ через

F(0, x₂,…,x_n) = _m (G₁ (x₂,…,x_n),…,G_m(x₂,…,x_n)),

F(x₁+1, x₂,…,x_n) = H(_1,m(F(x₁,x₂,…,x_n)),…,(_m,m(F(x₁,x₂,…,x_n))).

С помощью полной индукции по x₁ мы покажем, что справедливо: F_i(x₁,…,x_n) = _i,m(F(x₁,…,x_n)).

(i) _i,m(F(0, x₂,…,x_n)) = _i,m(_m(G₁(x₂,…,x_n),…,G_m (x₂,…,x_n))) =

= G_i (x₂,…,x_n) = F_i (0,x₂,…,x_n), 1 i  n.

(ii) _i,m(F(x₁+1,x₂,…,x_n)) =

= _i,m(H(_1,m (F (x₁,…,x_n)),…, _m,m(F(x₁,…,x_n)))) =

= _i,m(H(F₁ (x₁,…,x_n),…, F_m (x₁,…,x_n))) =

= _i,m(_m(…,H_i(F₁(x₁,…,x_n),…, F_m(x₁,…,x_n)),…)) =

= H_i (F₁(x₁,..,x_n),…,(F_m(x₁,…,x_n)) = F_i(x₁+1,x₂,…,x_n), 1in.

Так как _i,m – примитивно рекурсивная, то F_i тоже является примитивно рекурсивной (соотв. -рекурсивной). 

n-местный предикат P над  называется примитивно рекурсивным, если имеется примитивно рекурсивная функция H: ⁿ , такая, что:

Р истинно на (x₁,…,x_n) тогда и только тогда (обозн. Р(x₁,…,x_n)),

когда H (x_1,…,x_n) = 1;

Р ложно на (x_1,…,x_n) тогда и только тогда (обозн. Р(x₁,…,x_n)),

когда H (x_1,…,x_n) = 0.

Функция H называется характеристической функцией предиката Р. n‑местный предикат Т определяется тем, что он истинный на каждом (x₁,…,x_n) ⁿ.

Предложение 3.7. Пусть G₁,…,G_k – примитивно рекурсивные функции и Р₁,…,Р_k-1 – примитивно рекурсивные предикаты. Тогда функция F: ⁿ, такая, что

F(x₁,…,x_n) = (Р₁(x₁,…,x_n)G₁(x₁,…,x_n),



Р_k-1(x₁,…,x_n)G_k-1(x₁,…,x_n),

ТG_k(x₁,…,x_n))

будет примитивно рекурсивной.

Доказательство. Пусть H_i – характеристическая функция предиката Р_i, 1 i  k-1. Тогда справедливо:

F(x₁,…,x_n) = G₁(x₁,…,x_n)  H₁(x₁,…,x_n) +

+ G₂(x₁,…,x_n)  (1- H₁(x₁,…,x_n))  H₂(x₁,…,x_n) +



+ G_k(x₁,…,x_n)  (1-H₁(x₁,…,x_n))… (1-H_k-1(x₁,…,x_n)). 

Пример 3.5. (1) Функция «больше»: GR(x,y) = SGN (DIFF(x,y)), gr=sgn(diff).

(2) Функция «равно»:

GL(x,y)=DIFF(K(x,y),SUM(DIFF1(x,y),DIFF(x,y))),

gl = diff (k sum (diff1 diff)). 

Существуют хорошие основания предполагать, что -рекурсивные функции действительно являются интерпретацией понятия частично вы­числимых функций (в связи с алфавитом ) и тем самым понятия алго­ритма. Все предложенные интерпретации (некоторые из них мы еще обсу­дим) оказываются эквивалентными -рекурсивным функциям и все интуи­тивно описанные частично вычислимые функции могут быть точно опре­делены с помощью -рекурсивных функций. Это подводит к тезису Тью­ринга – Чёрча: «-рекурсивная функция является интерпретацией понятия частично вычислимой функции». Другими словами, что каждая частично вычислимая функция является -рекурсивной.

Мы хотим теперь эффективно нумеровать одноместные числовые ‑рекурсивные программы.

Их синтаксис имеет вид:

Pn  c  u  P(L)  [PP  P,

LPL  P.

Причем количество аргументов не учитывается. Для каждой про­граммы, однако, легко проверить, может ли она быть одноместной.

Исходный алфавит  =n, c, u       ,  содержит 9 символов. Мы эффективно нумеруем ^* с помощью С₉^. Пусть

w₀, w₁, w₂,…,w_n,…

– эффективная нумерация. Если мы хотим вычислить индекс одноместной программы w, мы ищем такой m, что w = w_m. Затем мы проверяем слова w_i, 0 i  m, являются ли они одноместными программами. Таким способом мы получим список одноместных программ

w, w, w,…,w = w_m = w.

Тем самым w получит индекс r. Если мы хотим перейти от индекса r к программе, то мы для 0ir таким же способом, что и выше, вычислим r‑тую одноместную программу.

Предложение 3.8. Одноместные -рекурсивные программы эффек­тивно нумеруются. 

С помощью эффективной нумерации одноместных -рекурсивных про­грамм мы строим теперь тотальную функцию H: , которая не является -рекурсивной.

Сначала сопоставим каждой -рекурсивной программе w её длину L (w); причем L (w) – число символов n, c, u     , , которые встречаются в w (круглые скобки не считают). Для каждой длины t 1 существует только конечное число программ w, таких, что L(w) = t. Мы определим функцию М:  через

М (0) = 0,

М (t) = max  w   w одноместная программа,

L (w) = t, w  определено t .

Вследствие того, что L (n _t) = t и n _t = t, t  1, М является тотальной функцией, для которой М (t)  t. Пусть H:  – тотальная функция

H (t) = М (2t)+1.

Предложение 3.9. Функция H не является -рекурсивной. (Согласно тезису Тьюринга – Чёрча: H не является вычислимой.)

Доказательство. Мы проведём непрямое доказательство. Пусть H – ‑рекурсивная функция. Тогда существует программа h, которая представ­ляет H. Пусть L(h) = t. Тогда мы рассмотрим программу h(n_t) с L(h(n_t)) = 2t. Отсюда h(n_t)(0)  М (2t). С другой стороны, h(n_t)(0) = h(t)= H(t) =М (2t)+1 и получим противоречие. 

С помощью тезиса Тьюринга – Чёрча получают, что функция H: , которая определяется следующим образом:

H(r) =

не является вычислимой.

Предложение 3.10. Пусть R – множество всех индексов одноместных -рекурсивных программ, которые завершаются, если индексы заменяются на 0. Тогда R   является неразрешимым, однако перечислимым множеством и, таким образом, является полуразрешимым. (Тем самым  –R неперечислимо.) 

(Позднее увидим, что предложения 3.9 и 3.10 эквивалентны известной проблеме останова машины Тьюринга.)

Пример 3.6. Определим последовательность функций G₀, G₁,…, G_n, … через

G₀ (у) =  (у),

G_х+1(0) = G_х(1),

G_х+1(у+1) = G_х(G_х+1(у)).

Каждая из этих функций примитивно рекурсивна. Функцию G_n+1 можно представить через программу g_n+1g_nnc)g_nu n, где g₀=n.

Можно показать, что тотальная функция F: ², которая определяется через F(x,y) = G_х(у),– -рекурсивная, но не примитивно ре­курсивная. Функция F может быть определена посредством

F (0, у) = у+1,

F (х+1, 0) = F (х, 1),

F (х+1, у+1) = F (х, F (х+1, у))

и является хорошо известной функцией Аккермана. 

Покажем теперь, что -рекурсивные функции частично вычислимы по Тьюрингу.

Предложение 3.11. Пусть H, G, G₁,…,G_m – функции, частично вычислимые по Тьюрингу. Тогда функция F также частично вычислима по Тьюрингу, если

(i) F получается путем замены из H и G₁,…,G_m,

(ii) F получается путем рекурсии из G и H,

(iii) F получается путем минимизации из G.

Доказательство. Мы покажем только (i). Пусть T_H, T_G…,T_G – односто­ронние детерминированные машины Тьюринга, которые вычис­ляют функции H, G₁,…,G_m. Мы строим машину Тьюринга Т, которая вы­числяет функцию F из (i).

Пусть H – m-местная и G_j – n-местная функция. Машина Тьюринга Т стартует при вводе данных х₁е…ех_n и изменяет их на $х₁е…ех_nZ_0. Она ко­пирует х₁е…ех_n справа от Z₀ и моделирует T_G. Если T_G останавливается (таким образом, если G₁ (х₁,…,х_n) определена), Т копирует содержимое ленты, которое стоит справа от Z₀ (причем символы пробела стираются), на место слева от $.

Пусть слева от $ уже стоит G₁ (х₁,…,х_n)е…еG_j-1(х₁,…,х_n). Т опять копи­рует х₁е…ех_n справа от Z₀ и моделирует T_G. Если T_G останавливается, то Т изменяет содержимое ленты слева от $ на G₁(х₁,…,х_n)е...е G_j-1(х₁,…,х_n)еG_j(х₁,..,х_n). Это выполняется для j=1,…,m. Затем $ и содержи­мое ленты справа от $ стирается, Z₀ помещается перед оставшимся содер­жимым ленты и моделируется T_H. Если машина Тьюринга продолжает стоять, то она вычислила H(G₁(х₁,…,х_n),…,G_m(х₁,…,х_n)). 

Предложение 3.12. Каждая -рекурсивная функция частично вычис­лима по Тьюрингу.

Доказательство. Функции следования, нуль-функции и функции про­екции, очевидно, вычислимы по Тьюрингу. Тогда, согласно предложению 3.11, все -рекурсивные функции частично вычислимы по Тьюрингу. 

Согласно тезису Тьюринга – Чёрча ясно, что каждая частично вычис­лимая по Тьюрингу функция -рекурсивна. Мы хотим это показать явно для случая одноместных числовых частично вычислимых по Тьюрингу функций.

Ограничимся машинами Тьюринга с алфавитом ленты {0,1}. При этом 0 означает пустой символ. Предположим, не уменьшая общности, что ма­шины Тьюринга имеют точно одно конечное состояние, обозначим через ,,.., – множество состояний, где – начальное состояние и – конеч­ное состояние. Пусть машина Тьюринга останавливается только в конечном состоянии . (Это означает, что функция перехода  вполне опре­делена на ,…,{0, 1}.)

Каждую ситуацию B_m…B₀SA₀…A_n можно представить четверкой чисел, а именно (i, S, M, N), где M =B_j2^j и N=A_j2^j.

В этом представлении прямой переход можно легко смоделировать.

Пусть ,S)  (, S₁, D), D, причем 1 означает движение вправо и 0 – движение влево. Проекции обозначаются через соответствующие ин­дексы и знак черты над состояниями опускается: ₁i,S) = j, ₂i,S) = S₁, ₃i,S) = D.

Для D=1 конфигурация, непосредственно следующая за конфигурацией B_m…B₀SA₀…A_n, а именно B_m…B₀S₁A₀…A_n, представляется четверкой (j,A₀,S₁+2M,(N-A₀₎). Пусть P(n) = n mod 2 и H(n)= n div 2. Тогда следую­щая четверка может быть записана как

(₁ i,S), P (N), ₂ i,S)+2M, H(N)).

Для D = 0 роли M и N меняются.

Получим, таким образом, для ik S , M, N

(i, S, M, N) ⊢ (₃ i, S) = 1(₁ i, S), P(N), ₂ i, S)+2M, H(N)),

₃ i, S) = 0(₁ i, S), P(M), H(M),₂ i, S)+2N)).

Продолжим  до тотальной функции :²³ посредством

  i, S) = (k+1,0,1) если i = 0 и S 0, либо

1 i k и S 2, либо

i  k+1 и S0.

Тем самым функции

R₁(i, S, M, N) = ₁ i, S),

R₂(i, S, M, N) = (₃ i, S) = 1  P (N), T  P (M)),

R₃(i, S, M, N) = (₃ i, S) = 1 ₂ i, S)+2M, TH(M)),

R₄(i, S, M, N) = (₃ i, S) = 1  H(N), T₂ i, S) +2N))

согласно предложению 3.7 – примитивно рекурсивные и моделируют пря­мой переход машины Тьюринга:

(i,S,M,N)⊢(R₁(i,S,M,N), R₂(i,S,M,N), R₃(i,S,M,N), R₄(i,S,M,N)).

Для того чтобы моделировать не только один прямой переход, но и произвольно много прямых переходов, мы введём функции T_j(t, i, S, M, N), 1j4, t0. Причем T₁(t, i, S, M, N) указывает состояние, которое получается из конфигурации (i, S, M, N) после t прямых переходов. Подобным же образом T₂(t, i, S, M, N) указывает символ, T₃(t, i, S, M, N) указывает число M и T₄(t, i, S, M, N) указывает число N, которые получаются после t прямых переходов.

Очевидно, справедливо:

T₁(0,i,S,M,N)=i, T₂(0,i,S,M,N)=S, T₃(0,i,S,M,N)=M, T₄(0,i,S,M,N)=N,

T_j(t+1,i,S,M,N)=R_j(T₁(t,i,S,M,N),T₂(t,i,S,M,N),T₃(t,i,S,M,N),T₄(t,i,S,M,N)), потому что t+1 прямых переходов из конфигурации (i, S, M, N) дают в результате то же самое, что и прямой переход из t-ой конфигурации.

Согласно предложению 3.6, функции T_j, 1j4, являются примитивно рекурсивными.

Теперь пусть начальная конфигурация машины Тьюринга есть , n  0. Этому соответствует четверка (1, SGN(n), 0, H(2ⁿ-1)). Тогда функции T_j(t, 1, SGN(n), 0, H(2ⁿ-1)), 1 j 4, дают конфигурацию машины Тьюринга после t прямых переходов. Если машина Тьюринга останавливается, то ей требуется в точности T₁(t, 1, SGN(n), 0, H(2ⁿ-1)) прямых переходов до остановки. Если она не останавливается, то T₁(t,1,SGN(n), 0, H(2ⁿ-1)) не определена. Не уменьшая общности, допустим, что машина Тьюринга ос­танавливается только в конфигурации вида 01^m. Тогда, если

T₄ ( T₁ (t, 1,SGN(n), 0, H(2ⁿ-1)), 1, SGN(n), 0, H(2ⁿ-1)) = 2^m-1,

m указывает значение функции F, вычисляемой машиной Тьюринга в точке n. Так как T₁, T₄ и «логарифмическая функция» примитивно рекурсивны, то F – -рекурсивная.

Таким образом, мы без использования тезиса Тьюринга – Чёрча пока­зали следующую эквивалентность.

Предложение 3.13. Семейство -рекурсивных функций совпадает с семейством функций, частично вычислимых поТьюрингу.

Тем самым -рекурсивные функции, машины Тьюринга и, согласно предложению 2.4, грамматики типа 0 и грамматики Ван-Вайнгаардена являются интерпретациями понятия алгоритма. Теперь рассмотрим вопрос разрешимости для машин Тьюринга и для контекстно-свободных языков.

Следующую проблему назовем «проблемой останова» машины Тьюринга. Пусть дана машина Тьюринга Т и слово w над своим входным алфавитом. Пусть указан алгоритм, который завершается для каждой пары Т, w и решает, останавливается или нет Т с входным словом w. «Проблема остановки машины Тьюринга с пустой лентой» является специальным случаем проблемы останова машины Тьюринга, а именно для случая w = . Так же, как и в доказательстве предложения 3.12, мы рассматриваем машины Тьюринга.

T = (…    ). 

Через такие машины Тьюринга можно представить все одноместные числовые -рекурсивные функции. Очевидно, что множество этих машин Тьюринга эффективно счетное. Таким образом, возможно каждой такой машине Тьюринга сопоставить некоторый индекс.

Предложение 3.14. Пусть S – множество всех индексов машин Тью­ринга вида , которые завершают работу при начальной конфигурации . Тогда S   неразрешимо.

Доказательство. Через доказательство предложения 3.11 и замечание к предложению 3.12 можно каждой -рекурсивной программе сопоставить машину Тьюринга вида , которая вычисляет ту же самую функцию, что и программа. Если бы S было разрешимым, то R по предложению 3.10 было бы разрешимым по следующему алгоритму. Для выбранного индекса r -рекурсивной программы строится индекс s соответствующей машины Тьюринга. И далее решают, то ли sS, то ли s–S. В первом случае выполняется rR, во втором случае – r–R.

Это рассуждение показывает, что разрешимость S влечет разрешимость R. Тем самым разрешимость S ведёт к противоречию с предложением 3.10. 

Предложение 3.15. Проблема остановки машины Тьюринга с пустой лентой и проблема остановки машины Тьюринга неразрешимы. 

Предложение 3.15 показывает более глубокую причину, почему функция H из предложения 3.9 невычислима: не существует алгоритма, который может установить, завершается или нет одноместная ‑рекур­сивная программа со входом 0. (Таким образом, также не существует алгоритма, который решает, определена или нет конкретная -рекурсивная функция для данного аргумента.)

Далее мы рассматриваем вопросы разрешимости контекстно-свободных грамматик. Эти вопросы разрешимости сводятся к проблеме остановки машины Тьюринга с пустой лентой.

Для каждой односторонней детерминированной машины Тьюринга T = (Q,   , q₀,F) мы строим две контекстно-свободные грамматики G₁,G₂ (которые зависят от T), такие, что

L(G₁) = $^R$   – конфигурации, ⊢^* – конечная конфигурация 

L(G₂) = q₀ Z₀ $ ^R$^*Q^*^*

Контекстно-свободная грамматика G₁ определяется посредством

G₁ =(S₁, T₁, U₁, V₁, W₁, X₁  Q $, P₁, S₁),

причем следующие продукции лежат в P₁:

(i) S₁T₁$S₁V₁, отсюда S₁^*T₁$…$T₁$V_1.

(ii) T₁zT₁z, z,

T₁qaU₁pb для (q,a) = (p,b,R), T₁cqaU₁bcp, для (q,a)=(p,b,L),

T₁q$pb, для (q,e) = (p,b,R), T₁c q $ b c p, для (q,e)=(p,b,L),

U₁z U₁ z, z,

U₁$;

эти правила позволяют производить выводы: T₁^*$^R, где   – конфигурации, ⊢.

(iii) V₁ qZ₀X₁, qF, W₁ zW₁, z,

V₁ Z₀W₁, W₁ q X₁, q F,

X₁ z X₁, z,

X₁ ;

эти правила позволяют производить выводы V₁^*, где  – конечная конфигурация.

Контекстно-свободная грамматика G₂ определяется посредством G₂=(S₂,T₂,U₂,V₂ Q$, P₂, S₂), причем следующие продукции лежат в P₂:

(i) S₂ q₀Z₀  S₂ $T₂, следовательно, S₂^*q₀ Z₀$T₂…$T_2.

(ii) T₂ zT₂z, z,

T₂ U₂,

U₂ qV₂q, qQ

V₂ zV₂z, z,

V₂$;

эти правила позволяют производить выводы:T₂^* ₁q₂$q, то есть T₂^* ^R $ , где  – конфигурация.

Предложение 3.16. L(G₁)L(G₂) тогда и только тогда, когда T оста­навливается с пустой лентой.

Доказательство. (i) пусть T останавливается с пустой лентой, таким образом: q₀Z₀⊢₁⊢₂⊢…⊢_n⊢_n+1, причем _n+1 – конечная конфигурация. Тогда в G₁ и G₂ найдутся следующие выводы:

S₁^* q₀ Z₀ $  $ ₁$  $ … $ _n $ $ _n+1,

S₂^*q₀ Z₀ $  $ ₁$ … $  $ _n $ $ _n+1.

Тем самым справедливо: L(G₁)L(G₂)  .

(ii) Пусть L(G₁)L(G₂)  . «Типичные» слова в L(G₁) и L(G₂) есть

₀ $ $ ₁$  $ … $ _n $ $ _n+1,

где _i, _i – конфигурации, причем _i ⊢_i+1 и _n+1 – конечная конфигурация;

q₀ Z₀ $ $ ₁$  $ ₂ … $ $ _m $ $ _m+1,

где _i – конфигурации.

Так как в L(G₁)L(G₂) лежит хотя бы одно слово, то должно сущест­вовать «типичное» слово в L(G₁) и «типичное» слово в L(G₂), которые совпадают. Отсюда следует n = m, ₀ = q ₀ Z_0, ₁= ₁, ₁= ₁, ₂ = ₂, ₂ = _2,…, _n= _m, _n = _m, _n+1 = _m+1, _n+1= _m+1.Таким образом: ₀=q₀Z_0, ₁=₁, ₂=₂,…,_n=_n, _n+1=_n+1, _i⊢_i+1 и _n+1 – конечная конфигурация. Поэтому мы получаем q₀Z₀ ⊢ ₁⊢ ₂⊢…⊢ _n⊢ _n+1, причем _n+1 – конечная конфигурация и Т останавливается с пустой лентой. 

Предложение 3.17. Проблема, является ли пустым пересечение двух контекстно-свободных языков, неразрешима. 

Доказательство. Так как для каждой машины Тьюринга Т мы можем эффективно построить грамматики G₁ и G₂, то разрешимость проблемы L(G₁)L(G₂)   влекла бы разрешимость проблемы остановки для машины Тьюринга с пустой лентой, что противоречит предложению 3.15. 

Можно показать, что G₁ и G₂ – однозначные грамматики. С помощью обычных методов можно построить контекстно-свободную грамматику G для L(G₁)  L(G₂). Тогда G будет однозначной тогда и только тогда, если L(G₁)L(G₂) = . Тем самым мы получим следующее предложение.

Предложение 3.18. Проблема, является ли контекстно-свободная грамматика однозначной, неразрешима. 

Рассмотрим далее язык

L = (L(G₁) L(G₂)) = (L(G₁))((L(G₁)), где _  Q$. Можно показать, что L – контекстно-свободный и существует некоторая эффек­тивно конструируемая из G₁ и G₂ контекстно-свободная грамматика G_1,2, такая, что L(G_1,2) = L.

Предложение 3.19. Проблема, порождает ли контекстно-свободная грамматика все слова над своим терминальным алфавитом, неразрешима.

Доказательство. Мы рассмотрим контекстно-свободную грамматику G_1,2 и алфавит _. Равенство L = справедливо тогда и только тогда, если L(G₁)L(G₂) = . 

Предложение 3.20. Пусть L_R – регулярный язык. Проблема, порождает ли контекстно-свободная грамматика G регулярный язык L_R, неразрешима.

Доказательство. Мы снова рассмотрим контекстно-свободную грам­матику G_1,2. Примем за L_R регулярный язык . 

Можно показать, что справедливо следующее обобщение предложений 3.17 и 3.20:

1. Проблема, является ли пересечение двух контекстно-свободных язы­ков снова контекстно-свободным, неразрешима.

2. Проблема, является ли контекстно-свободный язык регулярным, не­разрешима.

Мы теперь покажем, как с помощью грамматики Ван-Вайнгаардена можно построить интерпретатор для числовых примитивно рекурсивных программ.

Предложение 3.21. Для каждой числовой -рекурсивной функции F ^m существует грамматика Ван-Вайнгаардена, которая порождает язык

{b… b b F(n₁,…,n_m) определена }.

Доказательство. Для простоты проведем доказательство только для при­митивно рекурсивных функций и для m  . Пусть w n, c, u,        ^* – m-местная примитивно рекурсивная программа, m  , которая представля­ет функцию F. Мы определяем грамматику Ван-Вайнгаардена через мно­жество метапродукций R и множество схем продукций P.

Следующие метапродукции находятся в R:

(i) P   ncuPL  PP, Q   P L   PLP/

Из P выводимы примитивно рекурсивные программы.

(ii) N   aN b, A   NA M   N^m.

Справедливо: N ^*aⁿb, A ^* ab… ab, k  0, и M ^* ab… ab.

(iii) X   LA Y   AY  (L) AY .

Из X и Y выводимы необходимые контексты. Пусть X ^*x и Y^*y и v – n‑местная программа, которая представляет функцию V  ⁿ . Тогда справедливо:

 x v b…by  ^*  x b y.

Здесь символ  означает, что слово, которое может выводиться из РА (с правильным числом аргументов), должно «оцениваться».

Последующие схемы продукций лежат в Р:

(0)  start     M   w M  ,

 a A    a  A ,  b A    b  A ,  b    b.

Эти схемы продукций позволяют производить выводы

 start  ^* ab… ab  w ab… ab  

^* ab… ab  w ab… ab  ,

n₁,…,n_m, m   (начало вывода) и

 b  ^* b

(конец вывода).

(1)  X n N  Y     X a N Y  вычисляется функция следования,

(2)  X c  Y     X b Y   вычисляется нулевая функция,

(3) X uNAYXNY  вычисляется функция проекции ,

(4) (а)  X (P) A  Y     XPA Y  

(b) X (PL) A  Y    XPA (L) AY  проводится замена,

(5) (а)  X  PQ b A  Y     XPAY  

(b) X PQаAY  XQ PQ AAY; проводится рекурсия. 

Пример 3.7. Пусть w = sum, то есть w = un(u). Мы хотим вычислить sum (1,3).

 start   аbаааb   un (u)  аbаааb   

 аbаааb  un (u)  аbаааb    (5) (b)

 аbаааb  n (u) un (u)  bаааb  bаааb    (5)(а)

 аbаааb  n (u) u аааb  bаааb    (3)

 аbаааb  n (u) аааbbаааb    (4)(а)

 аbаааb  n u аааbbаааb    (3)

 аbаааb  n аааb   (1)

 аbаааb  ааааb  *

 аbаааbааааb. 

Конечно, подобное моделирование может быть проведено с по­мощью грамматик Ван-Вайнгаардена для -рекурсивных функций над алфавитом .

В заключение мы хотим построить грамматику Ван-Вайнгаардена с «библиотекой программ». В дополнение к программам n, c, u задаются следующие базовые программы k, k, k_i, n_i, u_i, sum, prod, exp,…,1 i  n, и их определения включаются в грамматику Ван-Вайнгаардена.

R расширяется следующими метапродукциями:

P:: = kk k_in_iu_isumprodexp,…,1 i  n,

P расширяется следующими схемами продукции:

 X n₁NYXnNY, Xn_i NYXn(n_i-1)NY, 2in,

 X kY XcY, XkYXn_i(c)Y, 1i n,

 X kNYX[cu]NY, XkNYXn_i(k)NY , 1i n,

 X k₀AYXk(u)AY, Xk_iAYXn_i(k₀)AY, 1i n,

 X u₁AYXuAY, Xu₁ AYX[u_i-1u]AY, 2  i  n,

 X sum A  Y    X  un (u)  AY ,

 X prod A Y    X  ksum (u u₃)  AY ,

 X exp A  Y     X  n(k) prod (u u₃) AY ,…

Пример 3.8. Мы хотим вычислить prod (1, 3).

 start   аbаааb  prod аbаааb   

 аbаааb  k sum (u u₃) аbаааb   

 аbаааb sum (uu₃)k sum (u u₃) bаааb bаааb   

 аbаааb  sum (u u₃) k аааb  bаааb   *

 аbаааb  sum (u u₃) bbаааb   

 аbаааb  sum u bbаааb  (u₃₎ bbаааb   

 аbаааb  sum b (u₃₎ bbаааb   

 аbаааb  sum b u₃ bbаааb  *

 аbаааb  sum bаааb  *

 аbаааbаааb. 