Введение

Изложенный здесь материал на протяжении ряда лет читался профес­сором Вернером Куихом в курсе «Теоретическая информатика» для сту­дентов Венского технического университета. Данное пособие может рас­сматриваться лишь как краткий конспект лекций, читаемых авторами для студентов математического факультета Калининградского госуниверси­тета, и не является заменой последних.

В пособии изложены основы теории формальных языков и грамматик, включая регулярные, контекстно-свободные грамматики и грамматики Ван Вайнгаардена, а также теория автоматов применительно к анализу фор­мальных языков, включая конечные автоматы, магазинные автоматы и машины Тьюринга. Далее даны основы теории алгоритмов и рекур­сивных функций, где особое внимание уделено вопросам вычислимости. В последней главе рассмотрены проблемы весьма актуальной сейчас тео­рии сложности.

В конце пособия приведены упражнения по изложенным темам вме­сте с их краткими решениями, что необходимо для практического закреп­ления материала.

1. Грамматики, автоматы и контекстно-свободные языки

Алфавит есть непустое конечное множество. Элементы алфавита назы­ваются символами. Пусть  – алфавит. Множество всех слов над , а именно

^ = {x₁x₂…x_n | x_i, 1in, n0}

вместе с операцией конкатенации образуют свободный моноид, порожден­ный , с единичным элементом  (для n = 0). Через |w| обозначим длину слова w^: |x₁…x_n| = n, n1, || = 0. Очевидно, выполняется |w₁w₂| = |w₁| + |w₂|. Отображение | |: ^  , где  – неотрицательные целые числа {0, 1, 2,...} есть гомоморфизм моноида <^, , > на моноид <, +, 0>.

Каждое подмножество L множества ^, т.е. L  ^, называется формаль­ным языком над . Пусть L₁ и L₂ формальные языки над , т.е. L₁, L₂  ^. То­гда определим произведение L₁ и L₂ как L₁L₂ = w₁w₂ | w₁L₁, w₂L₂}  ^.

Естественно <P(^), , {}> снова моноид. (Через P обозначим степень множества.) Он называется моноидом формальных языков.

Для L  ^ мы можем с помощью произведения определить степени:

L⁰ = {}, Lⁿ⁺¹ = LLⁿ = LⁿL, n0.

L^ определяется как L^ = ⁿ. Нам потребуется также L⁺ = ⁿ. Оче­видно, выполняется L^ = {}  L⁺ и L⁺ = LL^ = L^L.

В случае, если множество М содержит в точности один элемент, М = {а}, то мы также будем писать, если не возникнет путаницы, просто а. Справедливо: aⁿ = a … a (n раз) и a^ = {aⁿ | n0}.

Пусть S – множество. Каждое подмножество R множества SS, т.е. R  SS, называется (двухместным) отношением над S. Если (s₁,s₂)R, то мы пишем s₁Rs₂.

Пусть R – отношение над S. Транзитивное замыкание R⁺ определяется следующим образом: t₁R⁺t₂ в точности тогда, если существуют s₁, s₂, …, s_nS, n>1, такие что t₁ = s₁, t₂ = s_n и s_jRs_j+1, 1jn-1. Рефлексивное и тран­зитивное замыкание R^ определяется следующим образом: t₁R^t₂ в точно­сти тогда, если t₁ = t₂ или t₁R⁺t₂.

Грамматики есть математические системы, служащие для порождения формальных языков. Для определения синтаксиса языка программирова­ния они чрезвычайно важны. Множество синтаксически правильных про­грамм (причем содержание программ не принимается во внимание) может пониматься как формальный язык. Этот формальный язык определяется в общем случае через контекстно-свободную грамматику в нормальной форме Бэкуса.

Контекстно-свободная грамматика есть четверка G = (Ф, , P, S). Причем

1. Ф – алфавит, называемый алфавитом переменных, или нетерми­нальных символов;

2.  – алфавит, называемый алфавитом базовых, или терминаль­ных, символов, где Ф    , V = Ф  ;

3. P  Ф(Ф  )^ – конечное множество, называемое множест­вом продукций;

4. SФ – начальная переменная.

Пусть G = (Ф, , P, S) – контекстно-свободная грамматика. Тогда _G (или просто ) – отношение на V^, которое определено следующим обра­зом:    тогда и только тогда, когда   A,  =  и (A,)P.

Говорят, что  прямо выводит , или  может быть непосредственно выведено из .

Пусть отношение  (или просто ^) рефлексивное и транзитивное за­мыкание отношения _G. Говорят, что  выводит , или  может быть выведено из .

Пусть G = (Ф, , Р, S) – контекстно-свободная грамматика. Тогда обо­значим L(G) – язык, порожденный G, причем выполняется:

L(G) = {w | w^ и S w}.

Если (А,)Р, то пишем также А_G , или АP.

Пример 1.1. Пусть G = ({S}, {(,)}, P, S) с P = {S(S)S, S}. Тогда L(G) – есть множество всех корректных скобочных выражений над скоб­ками ( и ). Например: (())()  L(G), так как это выражение может быть вы­ведено из S:

S  (S)S  ((S)S)S  (()S)S  (())S  (())(S)S  (())()S  (())().

Таким образом, выполняется S ^* (())(), и тем самым (())() лежит в L(G).

Грамматика G’ = ({S}, {(,)}, P’,S) с P’ = {SSS, S(S), S} порож­дает тот же самый язык. Однако правила вывода имеют другую структуру:

S  SS  (S)S  ((S))S  (())S  (())(S)  (())().

Тем самым показано, что (())()L(G’). □

Если синтаксис языка программирования определяют через контек­стно-свободную грамматику, то продукции часто представляют в нормаль­ной форме Бэкуса. При этом переменные пишутся в форме <w>, где w – непустое слово над алфавитом V_Z. Если <w>  ₁, …, <w>  _n – все про­дукции с левой частью <w>, то пишут

<w>::= ₁|₂|…|_n.

Алфавиты Ф, V_Z,  не всегда указаны. Кроме того, разрешена следую­щая конструкция: _j может иметь вид ₁{₂}₃. Это означает, что возможны прямые выводы:

<w>  ₁₂ⁿ₃, n0.

Пример 1.2. В языке PASCAL константы определяются в разделе опи­сания констант. Синтаксис раздела описания констант задается следую­щими правилами (в нормальной форме Бэкуса):

<раздел описания констант>::= <пустой>|const<определение константы> {;<определение константы>};

<определение константы>::=<идентификатор константы> = <константа>

<идентификатор константы>::= <идентификатор>

<идентификатор>::= <буква>{<буква или цифра>}

<буква или цифра>::= <буква>|<цифра>

<буква>::= A|B|C|D|E|F|G|H|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z

<цифра>::= 0|1|2|3|4|5|6|7|8|9

<константа>::= <число без знака>|<знак><число без знака>|

<идентификатор константы>|<знак><идентификатор кон­станты>

<число без знака>::= <целое без знака>|<вещественное без знака>

<целое без знака>::= <цифра>{<цифра>}

<вещественное без знака>::= <целое без знака>.<цифра>{<цифра>}|

<целое без знака>.<цифра>{<цифра>}Е

<характеристика>|<целое без знака>Е

<характеристика>

<характеристика>::= <целое без знака>|<знак><целое без знака>

<знак>::= +|-

<пустой>::= 

Определение константы

const PI = 3.14; E = 2.73;

синтаксически правильно, так как существует вывод:

<раздел описания констант>

 const <определение константы>;<определение константы>;

 const <идентификатор константы>=<константа>;<определение кон­станты>;

const<идентификатор>=<константа>;<определение константы>;

 const <буква><буква или цифра>=<константа>;<определение кон­станты>;

 const <буква><буква>=<константа>;<определение константы>;

 const Р <буква> = <константа>;<определение константы>;

 const РI = <константа>;<определение константы>;

 const РI = <число без знака>;<определение константы>;

 const РI = <вещественное без знака>;<определение константы>;

const РI = <целое без знака><цифра><цифра>;<определение кон­станты>;

 const РI = <цифра><цифра><цифра>;<определение константы>;

^* const РI = 3.14;<определение константы>;

^* const PI = 3.14; E = 2.73; □

Формальный язык L  ^* называется контекстно-свободным тогда и только тогда, когда имеется контекстно-свободная грамматика G, такая что L(G) = L. Множество всех выражений, правильно заключенных в скобки, и множество всех синтаксически правильных определений констант есть, таким образом, контекстно-свободные языки.

Каждому выводу в контекстно-свободной грамматике G = (Ф, , Р, S) можно поставить в соответствие направленное дерево, так называемое де­рево вывода, узлы которого обозначаются символами из V:

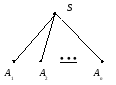
1. Выводу S  A₁A₂…A_n, A_jV, 1jn, соот­ветствует дерево вывода:

(2) Пусть выводу S ^ ₁A₂, ₁,₂  V^, AФ, соответствует дерево вывода:

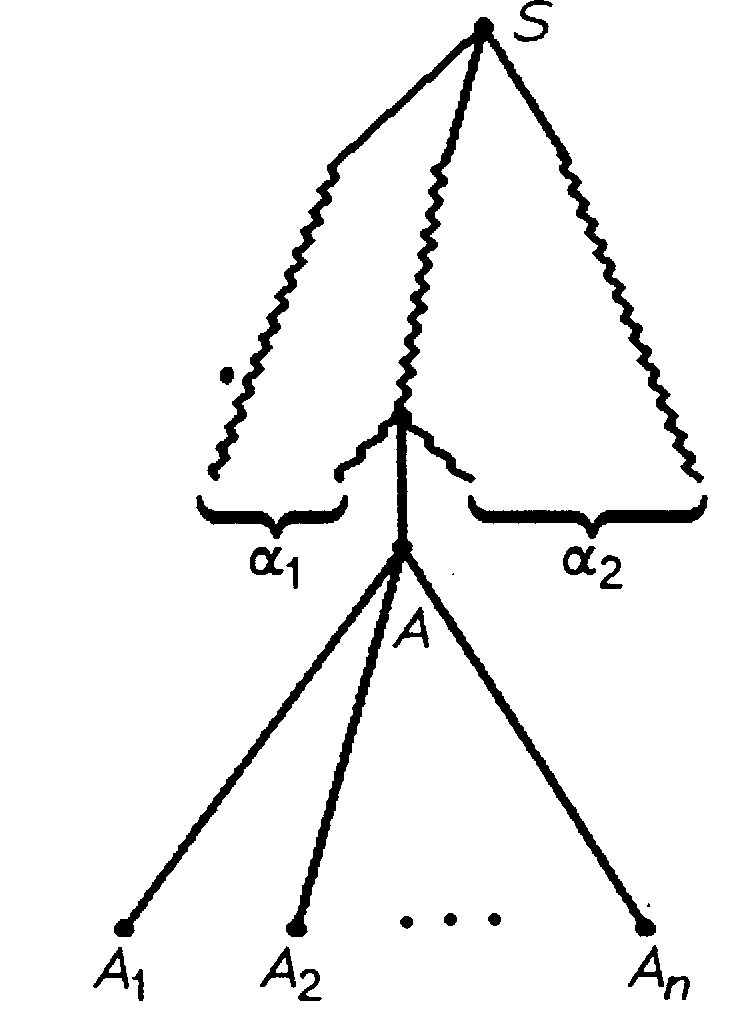
Тогда выводу S ^ ₁A₂  ₁A₁…A_n₂, A_jV соответствует дерево вы­вода:

Метки конечных узлов, если они при про­хож­дении по дереву вывода в положительном нап­равлении связываются воедино, дают в результа­те слово ₁A₁…A_n₂. Это слово называется результатом дерева вывода.

Пример 1.3. Выводам слова (())() в G и G’ соответствуют деревья вывода:

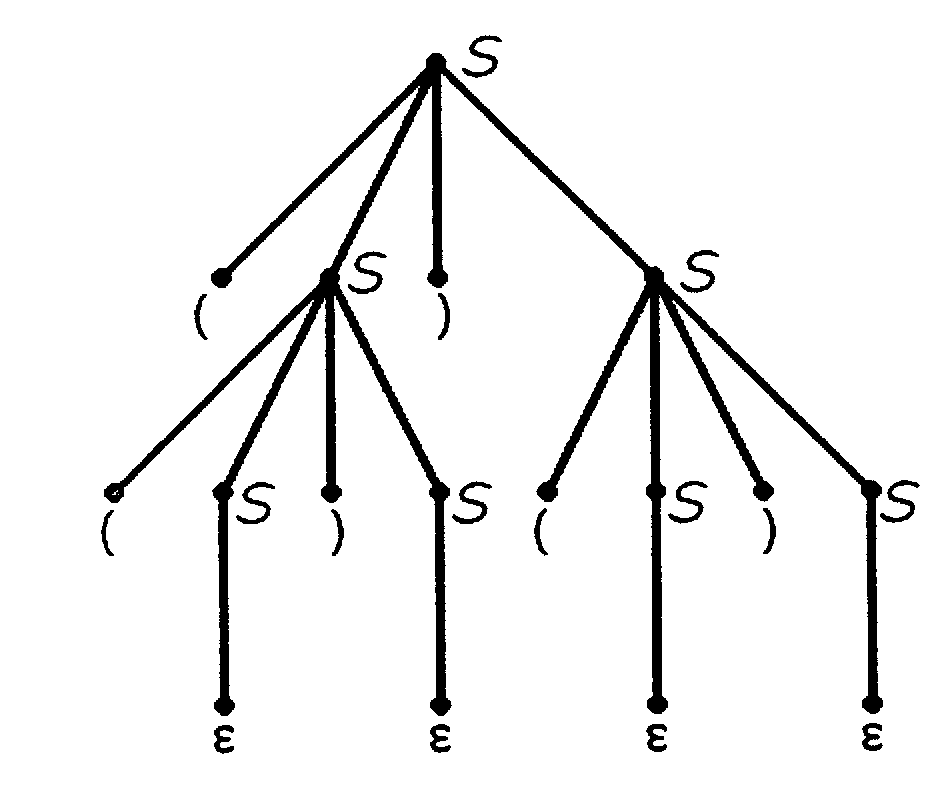
Пунктирные линии не принадлежат дереву вывода, которое соответст­вует правилу вывода в примере. Тем не менее дерево, состоящее из сплошных и пунктирных линий, также является деревом вывода с резуль­татом (())(). Таким образом, имеется два различных дерева вывода с ре­зультатом (())(). Это приводит к определению однозначной контекстно-свободной грамматики. Контекстно-свободная грамматика G называется однозначной тогда и только тогда, когда для каждого wL(G) найдется единственное дерево вывода. В противном случае она называется много­значной.

Пример 1.4. Пусть G = (Ф, , P, S),

где Ф = {оператор if,оператор};

 = {if, then, else, выражение, другой_оператор};

P = {оператор if::= if выражение then оператор

if выражение then операторelse оператор;

оператор::=оператор ifдругой_оператор};

S = оператор if.

L(G) описывает оператор if в PASCAL. Грамматика G – неоднозначна, так как «программа»: