- •Часть 2
- •Часть 2
- •Общие указания по выполнению расчетно-графических работ
- •Используемые обозначения
- •4. Изгиб Основные понятия и формулы
- •4.1. Расчет статически определимых балок
- •Основные определения
- •Примеры решения задач
- •4.1.1. Определение внутренних усилий в балках при плоском поперечном изгибе (задачи № 12–15)
- •Пример 2 Условие задачи
- •Решение
- •4.1.2. Проверка прочности балок при плоском поперечном изгибе (задачи № 16–19)
- •Пример 2 Условие задачи
- •Решение
- •Пример 3 Условие задачи
- •Решение
- •4.1.3. Определение перемещений и проверка жесткости балок (задачи № 19, 20)
- •Основные определения
- •Аналитический способ определения перемещений
- •Метод Максвелла – Мора определения перемещений
- •Пример 2 Условие задачи
- •Решение
- •Пример 2
- •Решение
- •4.2. Расчет статически определимых рам
- •Основные определения
- •4.2.2. Определение перемещений в рамах (задачи № 21, 22) Условие задачи
- •Решение
- •4.3. Расчет статически неопределимых балок и рам
- •Основные определения
- •Пример расчета трубопровода (задача № 26) Условие задачи
- •Решение
- •4.5. Определение напряжений и деформаций в криволинейном стержне
- •Основные определения
- •Пример расчета криволинейного стержня (задача № 27)
- •Сопротивление материалов
- •Часть 2
4.3. Расчет статически неопределимых балок и рам
Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 9 (§ 9.1–9.3).
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 9.
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 12 (§ 12.1–12.6).
Основные определения
Статически неопределимые балки и рамы – конструкции, в которых уравнений статики недостаточно для определения опорных реакций и внутренних усилий. Число связей, наложенных на статически неопределимую систему, больше того количества связей, которые обеспечивают геометрическую неизменяемость конструкции. Такими связями могут быть как опорные связи, так и стержни самой конструкции. Будем рассматривать балки и простые рамы, то есть такие конструкции, в которых связями, обеспечивающими геометрическую неизменяемость, являются опорные закрепления (опорные связи). Для обеспечения геометрической неизменяемости балки (рамы) в плоскости достаточно трех связей. Каждая связь запрещает какое-то перемещение. Шарнирно-подвижная опора запрещает перемещение по направлению, перпендикулярному плоскости опирания, и является одной связью. Шарнирно-неподвижная опора делает невозможными линейные перемещения по двум взаимно-перпендикулярным направлениям (вертикальному и горизонтальному) и соответствует двум связям, наложенным на конструкцию. Наконец, при наличии жесткого защемления на конце стержня становятся невозможными все перемещения: и вертикальное, и горизонтальное, и угол поворота, поэтому жесткое защемление представляет собой три связи, обеспечивающие геометрическую неизменяемость балки (рамы). Каждая дополнительная связь сверх трех для плоских систем превращает конструкцию в статически неопределимую. Такие дополнительные связи, которые не являются необходимыми для обеспечения геометрической неизменяемости конструкции, называются лишними.
Рис. 4.32. К расчету статически неопределимой
балки:
а – заданная статически неопределимая
балка;
б – основная система и условие
совместности деформаций (вариант 1);
в – основная система и условие
совместности деформаций
(вариант 2)
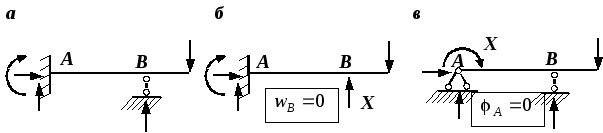
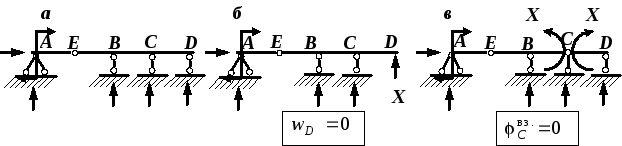
Рис. 4.33. К расчету статически неопределимой
балки с шарниром:
а – заданная статически неопределимая
балка;
б – основная система и условие
совместности деформаций (вариант 1);
в – основная система и условие
совместности деформаций (вариант
2)
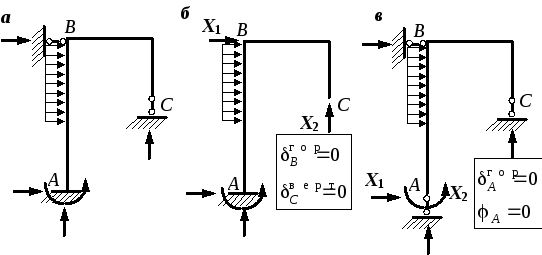
Рис. 4.34. К расчету статически неопределимой
рамы:
а – заданная статически неопределимая
рама;
б – основная система и условия
совместности деформаций (вариант 1);
в – основная система и условия
совместности деформаций
(вариант 2)
Для уменьшения в системе уравнений количества неизвестных, которые определяются в первую очередь, при расчете балок и рам чаще всего используют прием, связанный с выбором основной системы. Основная система – это статически определимая конструкция, полученная из заданной системы путем отбрасывания лишних связей. Реакции в отброшенных связях принято называть лишними неизвестными и обозначать Хi. Решение задачи (раскрытие статической неопределимости) сводится сначала к определению лишних неизвестных. Для их нахождения используются уравнения совместности деформаций – это условия кинематической эквивалентности основной и заданной систем, то есть равенства, приравнивающие нулю деформации по направлению отброшенных в основной системе связей. Количество уравнений совместности деформаций равно степени статической неопределимости. Зная величины лишних неизвестных, можно найти из уравнений равновесия остальные реакции. Обсудим подробно, как выбирать основную систему и записывать уравнения совместности деформаций.
На рис. 4.32, б, в
– 4.34, б, в
показаны по два варианта основных
систем, выбранных для заданных систем,
изображенных на рис. 4.32, а
– 4.34, а.
Балка на рис. 4.32, а
один раз статически неопределима, для
выбора основной системы необходимо
отбросить одну связь. В первом варианте
основной системы, изображенном на
рис. 4.32, б,
отброшена подвижная опора в точке В.
Вертикальная реакция в отброшенной
связи (лишняя неизвестная) обозначена
буквой Х.
Условие совместности деформаций для
этого варианта основной системы:
![]() – это условие, приравнивающее нулю
вертикальное перемещение (прогиб) в
точке В
балки, так как в заданной системе этот
прогиб был невозможен. Во втором варианте
на рис. 4.32, в
жесткое
защемление заменено шарнирно-неподвижной
опорой. Лишней неизвестной является
реактивный момент. Поскольку
в точке А
стал возможным
поворот сечения, то условие совместности
деформаций полагает этот угол поворота
равным нулю:
– это условие, приравнивающее нулю
вертикальное перемещение (прогиб) в
точке В
балки, так как в заданной системе этот
прогиб был невозможен. Во втором варианте
на рис. 4.32, в
жесткое
защемление заменено шарнирно-неподвижной
опорой. Лишней неизвестной является
реактивный момент. Поскольку
в точке А
стал возможным
поворот сечения, то условие совместности
деформаций полагает этот угол поворота
равным нулю:
![]() .
.
Для выбора основной
системы в дважды статически неопределимой
раме на рис. 4.34, а
требуется
отбросить две связи. На рис. 4.34, б, в
лишние неизвестные обозначены
Х1
и Х2.
В основной системе, показанной на
рис. 4.34, б,
стали возможны по сравнению с заданной
системой горизонтальное перемещение
в точке В
–
![]() и вертикальное перемещение в точке С
–
и вертикальное перемещение в точке С
–
![]() ,
поэтому эти перемещения необходимо
приравнять нулю. Это и есть условия
совместности деформаций для варианта
основной системы, показанной на
рис. 4.34, б:
,
поэтому эти перемещения необходимо
приравнять нулю. Это и есть условия
совместности деформаций для варианта
основной системы, показанной на
рис. 4.34, б:
![]() .
(4.26)
.
(4.26)
Аналогично для
основной системы, изображенной на
рис. 4.34, в,
условия совместности деформаций
следующие:
![]() .
.
Рис. 4.35. Взаимный угол поворота
сечений
около шарнира
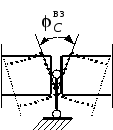
![]() (рис. 4.35). Этот взаимный угол поворота
соседних сечений в точке С
мы и должны положить равным нулю при
записи условия совместности деформаций:
(рис. 4.35). Этот взаимный угол поворота
соседних сечений в точке С
мы и должны положить равным нулю при
записи условия совместности деформаций:
![]() .
.
Для определения
лишних неизвестных необходимо найти
деформации в условиях совместности
деформаций любым способом. Как правило,
деформации находят методом Максвелла
– Мора с использованием правила
Верещагина. Удобно искать деформации
отдельно от заданной нагрузки
![]() и от лишних неизвестных
и от лишних неизвестных
![]() .
Например, условия совместности деформаций
(4.26) можно записать так:
.
Например, условия совместности деформаций
(4.26) можно записать так:
![]() ;
(4.27)
;
(4.27)
![]() .
(4.28)
.
(4.28)
Таким образом, для
дважды статически неопределимой системы
получаем систему уравнений из двух
уравнений с двумя неизвестными, из
которых и находим лишние неизвестные.
После определения
![]() и
и
![]() находим остальные неизвестные реакции
и строим окончательные эпюры внутренних
усилий N,
Q
и М,
используя уравнения статики.
находим остальные неизвестные реакции
и строим окончательные эпюры внутренних
усилий N,
Q
и М,
используя уравнения статики.
Окончательную эпюру изгибающих моментов для один раз статически неопределимой системы можно проверить, перемножив ее с эпюрой моментов от единичной силы12. Результатом этого перемножения должен быть ноль, то есть
![]() .
(4.29)
.
(4.29)
Условие (4.29) – это условие совместности деформаций, подтверждающее равенство нулю деформаций по направлению лишней неизвестной.
Примеры решения задач
4.3.1. Расчет статически неопределимой балки
(задача № 23)
Условие задачи
Рис. 4.36. Заданная балка
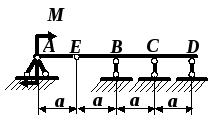
Решение
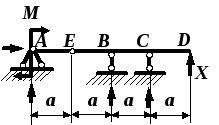
Рис. 4.37. Основная
система
![]() .
Прогиб в точке D
можно найти как сумму прогиба, вызванного
заданной нагрузкой (парой сил М)
и прогиба от лишней неизвестной Х,
т. е. условие совместности деформаций
можно записать так:
.
Прогиб в точке D
можно найти как сумму прогиба, вызванного
заданной нагрузкой (парой сил М)
и прогиба от лишней неизвестной Х,
т. е. условие совместности деформаций
можно записать так:
![]() .
.
Будем искать прогиб
методом Максвелла – Мора с использованием
правила Верещагина. Сначала найдем
![]() .
Для этого построим в основной системе
эпюры изгибающего момента от заданной
нагрузки (пары М
в данной задаче) – ММ
и
изгибающего момента от единичной
обобщенной силы, соответствующей
искомому перемещению, – М1.
Чтобы построить эпюру ММ,
найдем опорные реакции. Горизонтальная
реакция НА
в балках при отсутствии горизонтальной
составляющей нагрузки всегда равна
нулю – это следует из уравнения равновесия
"сумма проекций всех сил на горизонтальную
ось равна нулю". Для определения трех
других опорных реакций RA,
RB
и RC
составим три уравнения равновесия:
.
Для этого построим в основной системе
эпюры изгибающего момента от заданной
нагрузки (пары М
в данной задаче) – ММ
и
изгибающего момента от единичной
обобщенной силы, соответствующей
искомому перемещению, – М1.
Чтобы построить эпюру ММ,
найдем опорные реакции. Горизонтальная
реакция НА
в балках при отсутствии горизонтальной
составляющей нагрузки всегда равна
нулю – это следует из уравнения равновесия
"сумма проекций всех сил на горизонтальную
ось равна нулю". Для определения трех
других опорных реакций RA,
RB
и RC
составим три уравнения равновесия:
![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
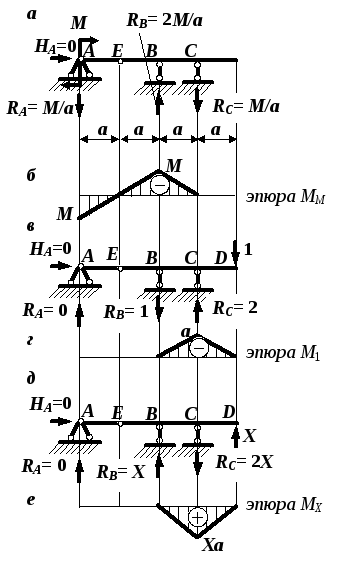
Рис. 4.38. Схемы балки и эпюры
изгибающих моментов:
а, б – от заданной нагрузки;
в, г– от единичной силы;
д, е– от лишней неизвестной
![]() .
.
![]() Теперь
ищем прогиб в точке D
от лишней неизвестной Х
–
Теперь
ищем прогиб в точке D
от лишней неизвестной Х
–
![]() .
Строим эпюру МХ
(рис. 4.38, е)
и перемножаем ее с эпюрой М1,
пользуясь правилом Верещагина:
.
Строим эпюру МХ
(рис. 4.38, е)
и перемножаем ее с эпюрой М1,
пользуясь правилом Верещагина:
![]() .
.
![]() Складываем
Складываем
![]() и
и
![]() ,
находим полное перемещение и в соответствии
с условием совместности деформаций
приравниваем его нулю:
,
находим полное перемещение и в соответствии
с условием совместности деформаций
приравниваем его нулю:
![]() .
.
Отсюда
![]() .
.
Рис. 4.39. Окончательные эпюры
внутренних усилий в заданной балке
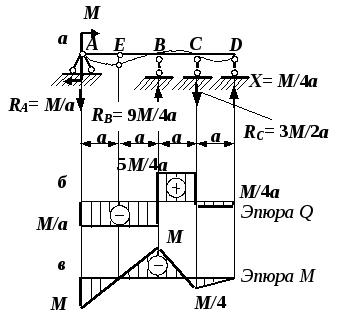
Заканчиваем решение проверкой результатов. Часто можно обнаружить ошибку, если построить изогнутую ось балки. Изогнутая ось должна удовлетворять как эпюре моментов, которая показывает, в какую сторону направлена выпуклость оси балки после изгиба, так и условиям закрепления балки. На рис. 4.39, а показана деформированная ось балки, удовлетворяющая указанным условиям. Заметим, что из-за наличия шарнира возможен перелом изогнутой оси в точке Е, так как сечения, примыкающие к шарниру поворачиваются на разные углы. Если не удается построить изогнутую ось так, чтобы она удовлетворяла всем условиям, то следует искать ошибку. Эта проверка носит качественный характер и не всегда дает возможность найти ошибку в вычислениях. Проверкой, подтверждающей правильность вычисления лишней неизвестной, является условие (4.29), то есть результатом перемножения окончательной эпюры М с эпюрой изгибающих моментов от единичной обобщенной силы М1 (по правилу Верещагина) должен быть ноль. Делая эту проверку, мы еще раз проверяем равенство нулю прогиба в точке D в нашей задаче, поскольку смыслом этого перемножения является согласно методу Максвелла – Мора определение перемещения по направлению обобщенной силы (прогиба в точке D в решаемой задаче). Проверим решение нашей задачи:
![]() .
.
4.3.2. Расчет статически неопределимой рамы
(задача № 24)
Условие задачи
В раме, показанной на рис. 4.40, требуется определить внутренние усилия и построить ось рамы после деформации. Жесткость всех стержней рамы одинакова и равна EI.
Решение
Рассматриваемая рама является один раз статически неопределимой и для выбора основной системы требуется отбросить одну лишнюю связь. Такой лишней связью будем считать шарнирно-
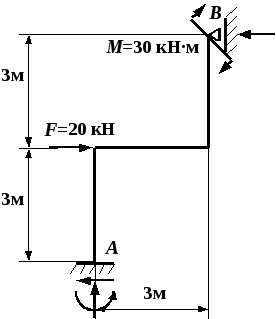
Рис. 4.40. Схема рамы с нагрузками
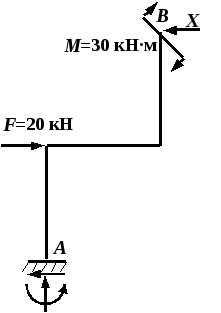
Рис. 4.41. Основная система
![]() .
Это перемещение складывается из
перемещения, вызванного всей заданной
нагрузкой
.
Это перемещение складывается из
перемещения, вызванного всей заданной
нагрузкой
![]() ,
и перемещения от лишней неизвестной
,
и перемещения от лишней неизвестной
![]() .
Тогда условие совместности деформаций
запишем так:
.
Тогда условие совместности деформаций
запишем так:
![]() .
.
Будем искать
перемещения методом Максвелла – Мора
с использованием правила Верещагина.
Для этого построим три эпюры изгибающих
моментов в основной системе: от заданной
нагрузки (рис. 4.42, а),
от единичной силы, соответствующей
горизонтальному перемещению в точке В
(рис. 4.42, б),
и от лишней неизвестной Х
(рис. 4.42, в).
Для определения
![]() перемножим
эпюры МР
и М1:
перемножим
эпюры МР
и М1:
![]()
![]() .
.
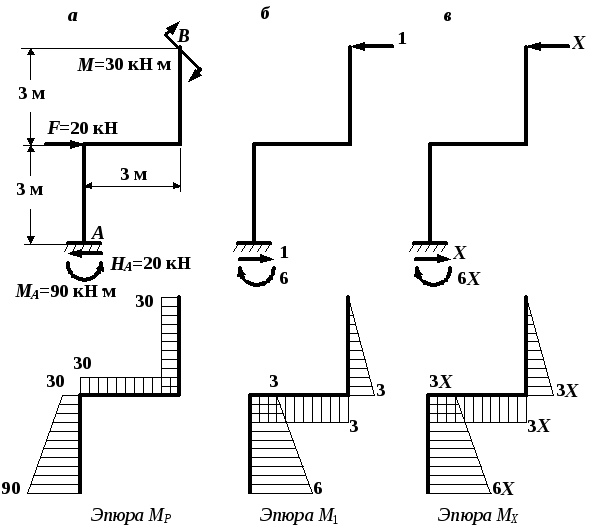
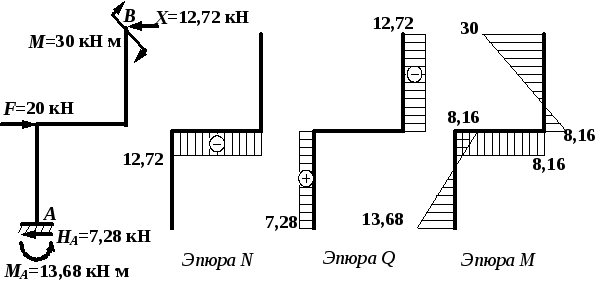
Рис. 4.42. Эпюры изгибающих моментов: а
– от заданной нагрузки;
б – от единичной силы; в – от
лишней неизвестной Х
Рис. 4.43. Окончательные эпюры внутренних
усилий
![]()
![]() .
.
Подставим найденные перемещения в условие совместности деформаций и найдем значение лишней неизвестной:
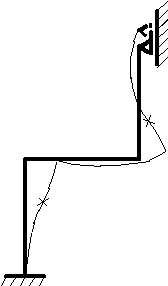
Рис. 4.44. Изогнутая ось рамы
![]() ,
откуда
,
откуда
![]() кН.
кН.
Строим окончательные эпюры внутренних усилий, приложив к основной системе все нагрузки, включая найденное значение Х (рис. 4.43). Выполним проверку, перемножив эпюру М с эпюрой М1.
![]()
![]() =147,24
– 147,3
0.
=147,24
– 147,3
0.
Изогнутая ось рамы, соответствующая эпюре изгибающих моментов (рис. 4.43, г), и условиям закрепления показана на рис. 4.44. Крестиками на рисунке отмечены точки перегиба оси.
4.4. РАСЧЕТ ПЛОСКОГО ТРУБОПРОВОДА
НА ТЕМПЕРАТУРНОЕ ВОЗДЕЙСТВИЕ И
ВНУТРЕННЕЕ ДАВЛЕНИЕ
Рекомендуемая литература
Камерштейн А. Г., Рождественский В. В., Ручинский М. Н. Расчет трубопроводов на прочность: Справочная книга. М.: Недра, 1969. Гл. 21, 27.
Основные определения
Рис. 4.45. Температурные компенсаторы
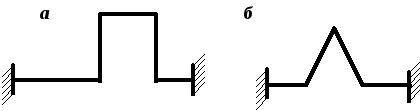
Рассматриваемые рамы являются три раза статически неопределимыми системами. Выберем основную систему для рамы, показанной на рис. 4.45, а, отбросив левую заделку (рис. 4.46). Лишними неизвестными являются реакции в защемлении: Х1, Х2 и Х3. В точке О поместим начало декартовой системы координат хОy. Положительное направление силы Х1 должно совпадать с направлением оси х, силы Х2 – с направлением оси y. Положительное направление пары сил Х3 должно соответствовать направлению поворота оси х к оси y. Можно показать, что решение канонической системы уравнений метода сил для выбранной основной системы дает такие формулы для определения лишних неизвестных:
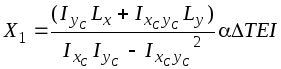 ;
(4.30)
;
(4.30)
 ;
(4.31)
;
(4.31)
![]() .
(4.32)
.
(4.32)
Рис. 4.46. К расчету трубопровода:
а – основная система;
б – точка С – упругий центр

Чтобы пояснить,
что такое хс,
yc,
![]() ,
,![]() и
и
![]() ,
будем рассматривать раму как плоскую
фигуру, состоящую из прямоугольников.
Одна сторона каждого прямоугольника
равна длине участка рамы, а другая
сторона (толщина) всегда равна 1. Например,
рама на рис. 4.46 считается плоской
фигурой, состоящей из пяти прямоугольников
с длинами соответственно l1,
l2,
l3
и 2l4
и толщиной
всех прямоугольников, равной 1. Тогда
хс,
yc
– координаты центра тяжести этой плоской
фигуры в системе координат xОy.
Центр тяжести фигуры (точка С
на рис. 4.46, б)
называется упругим
центром.
Через упругий центр проведем центральные
оси xc,
yc,
параллельные осям x,
y.
В формулах (4.30), (4.31)
,
будем рассматривать раму как плоскую
фигуру, состоящую из прямоугольников.
Одна сторона каждого прямоугольника
равна длине участка рамы, а другая
сторона (толщина) всегда равна 1. Например,
рама на рис. 4.46 считается плоской
фигурой, состоящей из пяти прямоугольников
с длинами соответственно l1,
l2,
l3
и 2l4
и толщиной
всех прямоугольников, равной 1. Тогда
хс,
yc
– координаты центра тяжести этой плоской
фигуры в системе координат xОy.
Центр тяжести фигуры (точка С
на рис. 4.46, б)
называется упругим
центром.
Через упругий центр проведем центральные
оси xc,
yc,
параллельные осям x,
y.
В формулах (4.30), (4.31)
![]() ,
,![]() и
и
![]() – осевые и центробежный моменты инерции
рассматриваемой плоской фигуры
относительно центральных осей xc,
yc.
– осевые и центробежный моменты инерции
рассматриваемой плоской фигуры
относительно центральных осей xc,
yc.
Напомним некоторые формулы. Координаты центра тяжести плоской фигуры находим так:
![]() ;
;
![]() ,
(4.33)
,
(4.33)
где А
– площадь фигуры. В данном случае, так
как толщина всех прямоугольников равна
единице, площадь равна сумме длин всех
участков рамы. Для рамы на рис. 4.46
![]() ;
Sx,
Sy
– статические моменты фигуры относительно
осей x,
y,
которые находятся как суммы статических
моментов каждого прямоугольника
относительно осей x,
y.
Статический момент каждого прямоугольника
равен произведению площади прямоугольника
на координату центра тяжести прямоугольника
в системе координат хОy.
;
Sx,
Sy
– статические моменты фигуры относительно
осей x,
y,
которые находятся как суммы статических
моментов каждого прямоугольника
относительно осей x,
y.
Статический момент каждого прямоугольника
равен произведению площади прямоугольника
на координату центра тяжести прямоугольника
в системе координат хОy.
Моменты инерции плоской фигуры вычисляются как суммы моментов инерции простых фигур, составляющих данную фигуру, в рассматриваемом случае момент инерции всей фигуры равен сумме моментов инерций прямоугольников единичной толщины. Для каждого прямоугольника справедливы формулы
![]() ;
(4.34)
;
(4.34)
![]() ;
(4.35)
;
(4.35)
![]() ,
(4.36)
,
(4.36)
где
![]() – площадь прямоугольника (
– площадь прямоугольника (![]() ,
,
![]() );
a,
b
– координаты центра тяжести прямоугольника
в системе координатных осей xc,
yc;
);
a,
b
– координаты центра тяжести прямоугольника
в системе координатных осей xc,
yc;
![]() ,
,
![]() – моменты инерции прямоугольника
относительно собственных центральных
осей x0,
y0,
параллельных осям xc,
yc.
Если ось
x0
(или y0)
расположена
вдоль рассматриваемого участка
трубопровода, то есть параллельна
стороне прямоугольника li,
то можно считать
– моменты инерции прямоугольника
относительно собственных центральных
осей x0,
y0,
параллельных осям xc,
yc.
Если ось
x0
(или y0)
расположена
вдоль рассматриваемого участка
трубопровода, то есть параллельна
стороне прямоугольника li,
то можно считать
![]() (или
(или
![]() ).
Если же ось x0
(или y0)
перпендикулярна
стороне li,
то
).
Если же ось x0
(или y0)
перпендикулярна
стороне li,
то
![]() .
В формуле (4.36) учтено, что центробежный
момент инерции прямоугольника
.
В формуле (4.36) учтено, что центробежный
момент инерции прямоугольника
![]() относительно
собственных осей x0,
y0
равен нулю,
так как эти оси являются главными осями
инерции прямоугольника.
относительно
собственных осей x0,
y0
равен нулю,
так как эти оси являются главными осями
инерции прямоугольника.
После определения величин лишних неизвестных по формулам (4.30) – (4.32) строим эпюры внутренних усилий в основной системе, как в обычной статически определимой раме. Эпюру изгибающих моментов можно проверить следующим образом. В упругом центре приложим найденные силы Х1 и Х2, нарисовав их в масштабе. Определим графически равнодействующую этих сил. Точки пересечения линии действия этой равнодействующей с осью рамы – это точки, в которых изгибающий момент должен равняться нулю (точки A, B, D на рис. 4.46, б).
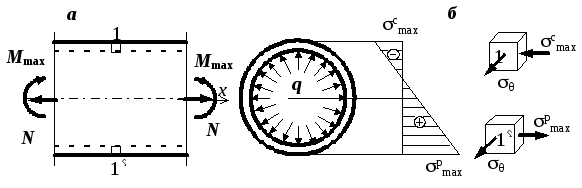
Построив эпюры внутренних усилий, проверим прочность конструкции, имея в виду, что поперечное сечение стержней рамы – труба и, кроме температурного воздействия, труба испытывает действие внутреннего давления. Максимальные нормальные напряжения х, действующие на площадках, перпендикулярных оси трубы, находим, складывая напряжения от продольной силы и максимального изгибающего момента в опасном сечении рамы13:
![]() .
(4.37)
.
(4.37)
Для проверки прочности трубы из пластичного материала по формуле (4.37) находим максимальное по модулю напряжение. Если труба выполнена из хрупкого материала, при проверке прочности важен знак напряжений. Кольцевое напряжение , возникающее от внутреннего давления q, определяем по формуле
![]() ,
(4.38)
,
(4.38)
Рис. 4.47. К определению напряжений в
трубе:
а – распределение напряжений х
в опасном сечении;
б – напряженное состояние опасных
точек