
- •220400 Алгебра и геометрия Толстиков а.В.
- •Поверхности второго порядка в пространстве r3
- •2. Поверхности вращения.
- •3. Цилиндрические поверхности.
- •4. Конические поверхности.
- •5. Эллипсоиды
- •6. Однополостные гиперболоиды и его прямолинейные образующие.
- •7. Двуполостные гиперболоиды
- •8. Эллиптические параболоиды.
- •9. Гиперболические параболоиды и его прямолинейные образующие
- •Классификация кривых второго порядка.
- •Классификация поверхностей второго порядка.
- •11. Приведение кривой второго порядка и поверхности второго порядка к каноническому виду по методу собственных значений
7. Двуполостные гиперболоиды
Определение 1. Поверхность, которая в некоторой прямоугольной системе координат имеет уравнение
![]()
 ,
(15)
,
(15)
называется двуполостным гиперболоидом, a > 0, b > 0, c > 0. Числа a, b, c называются полуосями двуполостным гиперболоидом.
Исследуем поверхность двуполостного гиперболоида по уравнению (15). Так как переменные входят в уравнение (15) в четной степени, то вместе с точкой (x, y, z) двуполостному гиперболоиду принадлежат все восемь точек (x, y, z) (с произвольными комбинациями знаков). Таким образом, двуполостной гиперболоид симметричен относительно, всех трех координатных плоскостей и начала координат. Он пересекает координатные оси Oz, Oy соответственно в точках (a, 0, 0), (0, b, 0), которые называются вершинами двуполостного гиперболоида.
Исследуем методом сечений поверхность двуполостного гиперболоида, проведя его сечения плоскостями, параллельными координатным. Пересекая его плоскостями z = h (- < h < +), параллельными плоскости Oxy, получим при h > c и h < -c и в сечении эллипсы, при -c <h < c - мнимый эллипс.
Пересекаем двуполостной гиперболоид плоскостями x = h (- < h < +), параллельными плоскости Oyz. Получим в сечении гиперболы. Аналогичная картина будет при сечении двуполостного гиперболоида плоскостями, параллельными плоскости Oxz.
8. Эллиптические параболоиды.
Определение 1. Поверхность, которая в некоторой прямоугольной системе координат имеет уравнение
![]() ,
(17)
,
(17)
называется эллиптическим параболоидом, p > 0, q > 0, c > 0. Числа p и q называются параметрами эллиптического параболоида.
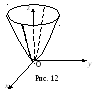
 Исследуем
поверхность эллиптического параболоида
по уравнению (17). Так как переменные x
и y входят в
уравнение (17) в четной степени, то вместе
с точкой (x, y, z)
эллиптическому параболоиду
принадлежат четыре точки (x,
y,
z) (с произвольными
комбинациями знаков). Таким образом,
эллиптический параболоид симметричен
относительно, координатных плоскостей
Oxz и
Oyz. Он пересекает
координатные оси в начале координат.
Эта точка называется вершиной
эллиптического параболоида.
Исследуем
поверхность эллиптического параболоида
по уравнению (17). Так как переменные x
и y входят в
уравнение (17) в четной степени, то вместе
с точкой (x, y, z)
эллиптическому параболоиду
принадлежат четыре точки (x,
y,
z) (с произвольными
комбинациями знаков). Таким образом,
эллиптический параболоид симметричен
относительно, координатных плоскостей
Oxz и
Oyz. Он пересекает
координатные оси в начале координат.
Эта точка называется вершиной
эллиптического параболоида.
Исследуем методом сечений поверхность эллиптического параболоида, проведя его сечения плоскостями, параллельными координатным. Пересекая его плоскостями z = h (- < h < +), параллельными плоскости Oxy, получим при h > 0 в сечении эллипсы, при h < 0 - мнимый эллипс.
Пересекаем эллиптический параболоид плоскостями x = h (- < h < +), параллельными плоскости Oyz. Получим в сечении параболу . Аналогичная картина будет при сечении эллиптического параболоида плоскостями, параллельными плоскости Oxz.
9. Гиперболические параболоиды и его прямолинейные образующие
Определение 1. Поверхность, которая в некоторой прямоугольной системе координат имеет уравнение
![]() ,
(19)
,
(19)
называется гиперболическим параболоидом p > 0, q > 0. Числа p, q называются параметрами гиперболического параболоида.
Исследуем поверхность гиперболического параболоида по уравнению (19). Так как переменные x и y входят в уравнение (19) в четной степени, то вместе с точкой (x, y, z) гиперболическому параболоиду принадлежат четыре точки (x, y, z) (с произвольными комбинациями знаков). Таким образом, гиперболический параболоид симметричен относительно координатных плоскостей Oxz, Oyz. Он пересекает координатные оси в начале координат. Эта точка называется вершиной гиперболического параболоида.
Исследуем методом сечений поверхность гиперболического параболоида, проведя его сечения плоскостями, параллельными координатным. Пересекая гиперболический параболоид плоскостями z = h (- < h < +), параллельными плоскости Oxy, получим при h 0 в сечении гиперболы.
Пересекаем гиперболический параболоид плоскостями x = h (- < h < +), параллельными плоскости Oyz. Получим в сечении параболу.
П ересекаем
гиперболический параболоид плоскостями
y = h
(-
< h
< +),
параллельными плоскости Oxz.
Получим в сечении параболу . Применим
полученные исследования к построению
поверхности гиперболического параболоида
(см. рис. 13).
ересекаем
гиперболический параболоид плоскостями
y = h
(-
< h
< +),
параллельными плоскости Oxz.
Получим в сечении параболу . Применим
полученные исследования к построению
поверхности гиперболического параболоида
(см. рис. 13).
Уравнение гиперболического параболоида (19) можно записать в виде
![]() .
(20)
.
(20)
Составим две системы уравнений первой степени
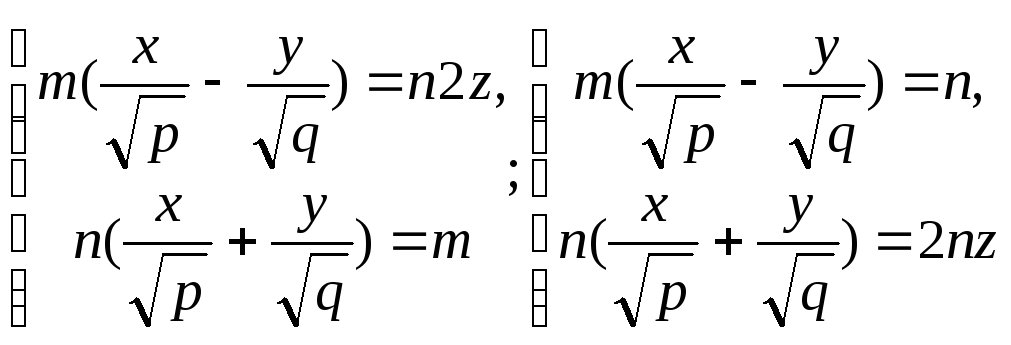 ,
(21)
,
(21)
где m и n произвольные действительные параметры, которые одновременно не равны нулю.
Для любых m и n, одновременно не равных нулю, каждая из систем (21) определяет прямую, и эти прямые пересекаются (проверить это). Если мы перемножим уравнения в каждой из систем (21) почленно и сократим, полученное равенство, на mn, то получим уравнение (19). Поэтому любая точка (x, y, z) , принадлежащая прямым (3), находится на поверхности (19).
Прямые, принадлежащие каждому из двух семейств прямых, определяемых системами (21) называются прямолинейными образующими гиперболического параболоида (см. рис. 14). При нахождении прямолинейных образующих можно один из двух параметров m или n в системах (21) полагать равным единице.
