Экспериментальное определение характеристик рассеивания

Экспериментальные методы определения характеристик рассеивания позволяют наблюдать рассеивание таким, каким оно есть на самом деле, но их использование связано с большой сложностью проведения опытных стрельб в определенных метеоусловиях, высокой стоимостью натурных экспериментов. По результатам N опытных стрельб определяют декартовы координаты точек попадания X_i, Y_i, где i – номер выстрела в очереди или снаряда в залпе. Координаты центра рассеивания m_x, m_y оценивают средним арифметическим этих результатов, дисперсию рассеивания – исправленной статистической дисперсией по формулам (4.34), (4.38):

,

, .

Имитационное моделирование рассеивания

Имитационное моделирование способно заменить полигоные испытания на кучность стрельбы, если обеспечена адекватность математической и стохастической моделей условиям испытания на кучность. Это значит, что при определении одинаковых условий для стрельбы и расчета траектории все случайные факторы, сопровождающие стрельбу, также адекватно моделируются (разыгрываются) в имитационном эксперименте. Рассматривая результаты стрельбы как векторную функцию случайных аргументов Y = (X), требования к имитационной модели можно свести к точному алгоритмическому моделированию функции  и адекватной вероятностной модели аргументов X. Статистическая обработка результатов имитационного моделирования по формулам (4.34), (4.38) не составляет проблемы, так как в имитационном эксперименте контролируются все случайные факторы, а число испытаний N может быть достаточно большим.

Полунатурное моделирование рассеивания

Полунатурное моделирование отличается от имитационного тем, что некоторые сложные частные модели исследуемого объекта реализуются физическим (натурным) компонентом, который осуществляет свою часть преобразования  случайного аргумента X.

Законы распределения функций случайных величин

Если для определения числовых характеристик функций СВ достаточно знать законы распределения аргументов, то для вычисления вероятности попадания значения функции в заданную область нужен закон распределения функции. Так, минимальная дисперсия отклонения после однократной коррекции Y = X – a sign(X) была найдена на основании известного закона f_X(x), но для вычисления P(|Y| < y) надо знать закон распределения f_Y(y).

Функция распределения монотонных функций св

Рис. 9.4. Монотонные функции СВ X

Если (x) строго монотонна, обратная функция x = (y) ^– 1  (y) однозначна (рис. 9.4), поэтому событие (Y < y) эквивалентно событию (X < (y)), если (x) возрастающая, или событию (X > (y)), если (x) убывает, следовательно,

, если (x) возрастающая, , если (x) убывающая,

(9.21) (9.22)

Пример 5: способ получения реализаций св с заданным законом распределения

Функция распределения F любой СВ монотонно возрастающая, обратная к ней (x)  F ^–1(x) тоже возрастающая c областью определения в интервале [0, 1]. Пусть СВ X распределена по равномерному закону в интервале [0, 1], т.е. F_X(x) = x на этом интервале. Закон распределения СВ Y = F ^–1(X) можно получить, подставляя (y) = ^–1(y) = F(y) в формулу (9.21):

F_Y(y) = F_X((y)) = (y) = F(y).

Таким образом, чтобы получить случайные реализации СВ Y, имеющей функцию распределения F(y), нужно преобразовать реализации датчика случайных чисел rand обратной функцией к F(y): y = F ^–1(rand).

Плотность распределения монотонных функций св

Если СВ X непрерывна, имеет плотность f_X(x) и функция (x) дифференцируема, плотность СВ Y получим дифференцированием F_Y(y):

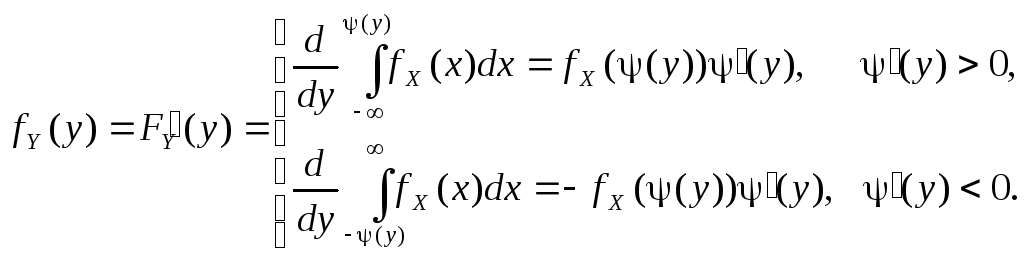
Функция плотности f_Y(y), как и полагается, положительна в обоих выражениях. Их можно заменить общей формулой, согласно которой плотность СВ Y равна плотности f_X(x) при соответствующем значении аргумента x = (y), умноженной на якобиан |(y)|:

fY(y) = fX((y))|(y)|.

(9.23)