- •1. Возрастание и убывание функции.
- •Примеры
- •2. Экстремумы функции.
- •Примеры
- •3. Наибольшее и наименьшее значения функции.
- •Примеры
- •2Способ (с помощью второй производной)
- •4. Выпуклость функции и точки перегиба.
- •Примеры
- •5. Асимптоты.
- •Примеры
- •6. Построение графиков функций.
- •6.7. Исследовать параметрически заданную кривую
- •И построить ее.
- •Литература
- •Содержание
- •Учебное издание Александр Борисович Дюбуа Светлана Николаевна Машнина
Рязанский филиал
Государственного образовательного учреждения
высшего профессионального образования
«московский государственный университет
экономики, статистики и информатики (мэси)» ____________________________________________________________
Кафедра гуманитарных и естественнонаучных дисциплин
А.Б. ДЮБУА, С.Н. МАШНИНА
математиЧЕСКИЙ АНАЛИЗ: исследование
функций одной переменной
Допущено учебно-методическим советом Рязанского филиала
государственного образовательного учреждения высшего профессионального образования «Московский государственный университет экономики, статистики и информатики (мэси)» в качестве учебного пособия для студентов Рязанского филиала МЭСИ, обучающихся по специальностям:
080801 – «Прикладная информатика (по областям)»; 080111 – «Маркетинг»; 080507 – «Менеджмент организаций»; 080503 – «Антикризисное управление»; 080109 – «Бухгалтерский учет, анализ и аудит»;080105 – «Финансы и кредит».
Протокол №3 от19 января.2011 г.
Рязань 2011
УДК 517.2
ББК 22.15
Д11
Рецензент:
каф. высшей математики Рязанского государственного радиотехнического университета (зав. каф. К.В. Бухенский, к.ф.-м.н., доцент).
Дюбуа А.Б., Машнина С.Н. Математический анализ: исследование функций с помощью производных, – Рязань: Рязанский филиал МЭСИ, 2011 г. – 48 с.
Составлено в соответствии с Государственным образовательным стандартом по высшей математике для специальностей: 080801 – «Прикладная информатика (по областям)»; 080111 – «Маркетинг»; 080507 – «Менеджмент организаций»; 080503 – «Антикризисное управление»; 080109 – «Бухгалтерский учет, анализ и аудит»; 080105 – «Финансы и кредит».
-
© Рязанский филиал ГОУВПО «Московский государственный университет экономики, статистики и информатики (МЭСИ)», 2011
1. Возрастание и убывание функции.
Для того чтобы
дифференцируемая на интервале
![]() функция
функция
![]() была возрастающей на этом интервале,
необходимо и достаточно, чтобы выполнялось
условие
была возрастающей на этом интервале,
необходимо и достаточно, чтобы выполнялось
условие
![]() при всех
при всех
![]() .
.
Аналогично, условие
![]() при всех
при всех
![]()
является необходимым
и достаточным для убывания дифференцируемой
на интервале
![]() функции
функции
![]() .
.
Примеры
1.1. Доказать,
что функция
![]() строго возрастает на промежутке
строго возрастает на промежутке
![]() .
.
Так как
 ,
,
то для всех
![]() функция
функция
![]() является строго возрастающей на всей
области определения.
является строго возрастающей на всей
области определения.
1.2. Доказать,
что если
![]() ,
то
,
то
![]() .
.
Пусть
![]() ,
тогда
,
тогда
![]() .
Эта функция дифференцируема на интервале
.
Эта функция дифференцируема на интервале
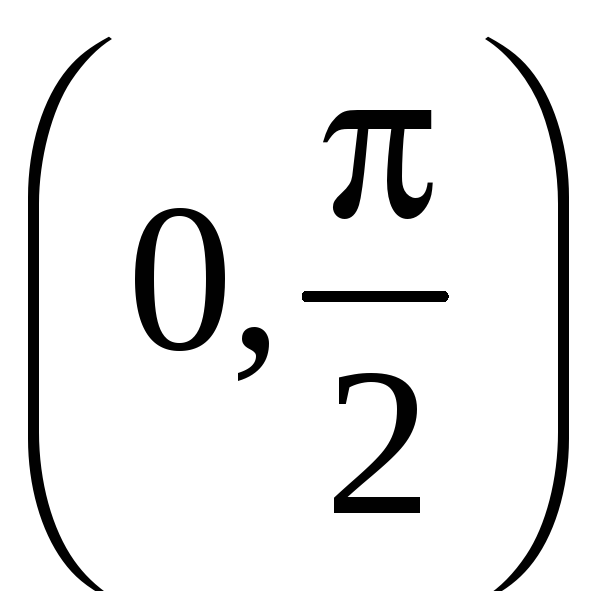 ,
причем
,
причем
![]() ,
,
то для всех
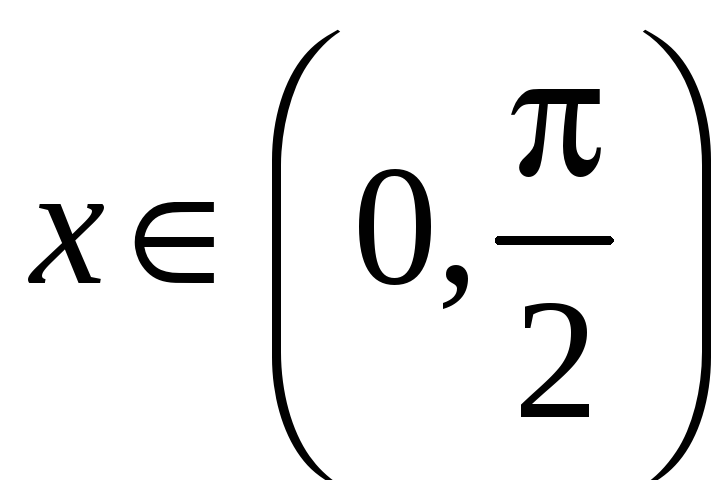 функция
функция
![]() строго убывает на интервале
строго убывает на интервале
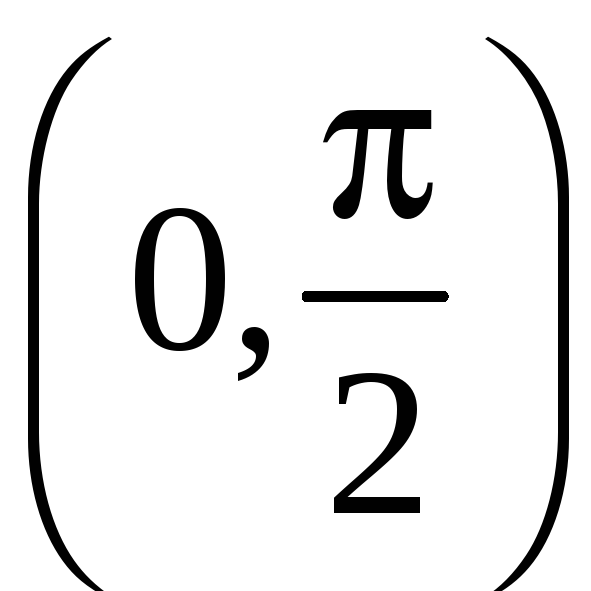 .
Поэтому
.
Поэтому
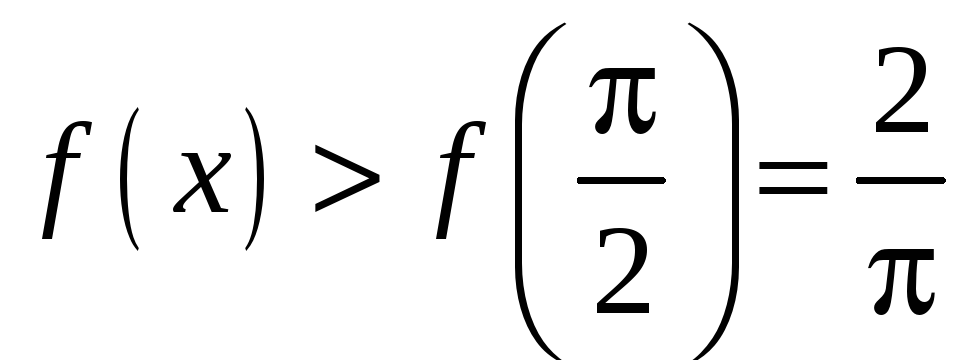
для всех
 .
.
То есть выполнено
![]()
![]()
![]() .
.
2. Экстремумы функции.
Необходимое условие экстремума.
Точки экстремума
функции
![]() следует искать среди тех точек области
определения, в которых производная этой
функции либо равна нулю, либо не
существует. Точки, в которых производная
данной функции равна нулю, называет
стационарными точками этой функции, а
точки, в которых функция непрерывна, а
её производная либо равна нулю либо не
существует,— ее критическими точками.
следует искать среди тех точек области
определения, в которых производная этой
функции либо равна нулю, либо не
существует. Точки, в которых производная
данной функции равна нулю, называет
стационарными точками этой функции, а
точки, в которых функция непрерывна, а
её производная либо равна нулю либо не
существует,— ее критическими точками.
Достаточные условие экстремума.
1) Если
![]() меняет знак с минуса на плюс при переходе
через точку
меняет знак с минуса на плюс при переходе
через точку
![]() ,
то
,
то
![]() - точка строгого минимума функции
- точка строгого минимума функции
![]() .
Если
.
Если
![]() меняет знак с плюса на минус при переходе
через точку
меняет знак с плюса на минус при переходе
через точку
![]() ,
то
,
то
![]() - точка строгого максимума функции
- точка строгого максимума функции
![]() .
.
2) Пусть
![]() и существует вторая производная
и существует вторая производная
![]() .
Тогда, если
.
Тогда, если
![]() ,
то
,
то
![]() - точка строгого минимума функции
- точка строгого минимума функции
![]() .
Если
.
Если
![]() ,
то
,
то
![]() - точка строгого максимума функции
- точка строгого максимума функции
![]() .
.
Примеры
2.1. Найти точки экстремума функции
![]() .
.
Функция
дифференцируема на множестве всех
действительных чисел, поэтому все её
точки экстремума содержатся среди
стационарных точек функции, являющихся
корнями уравнения
![]() ,
т.е. уравнения
,
т.е. уравнения
![]() ,
,
которое имеет
корни
![]() ,
,
![]() ,
,
![]() .
Для удобства составим таблицу:
.
Для удобства составим таблицу:
|
|
|
|
|
|
|
возрастает |
|
|
0 |
|
|
|
|
возрастает |
|
|
0 |
max |
|
|
|
убывает |
|
|
0 |
min |
|
|
|
возрастает |
Из таблицы видно,
что
![]() ,
,
![]() - точки строгого максимума и минимума,
а
- точки строгого максимума и минимума,
а
![]() не является точкой экстремума.
не является точкой экстремума.
2.2. Найти точки экстремума функции
![]() .
.
Прежде всего,
отметим, что функция
![]() — четная, непрерывная на
— четная, непрерывная на
![]() ,
дифференцируемая на
,
дифференцируемая на
![]() ,
кроме точек
,
кроме точек
![]() .
Эквивалентное представление функции:
.
Эквивалентное представление функции:
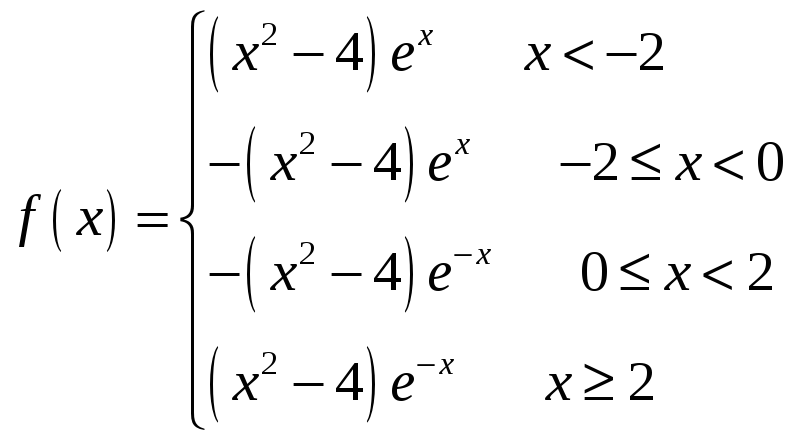 .
.
Производная функции
![]() равна
равна
 ,
,
критическими
точками которой будут
![]() ,
,
![]() ,
,
![]() .
.
Составим таблицу
|
|
|
|
|
|
|
возрастает |
|
|
0 |
max |
|
|
|
убывает |
|
|
не существует |
min |
|
|
|
убывает |
|
|
не существует |
max |
|
|
|
убывает |
|
|
не существует |
min |
|
|
|
возрастает |
|
|
0 |
max |
|
|
|
убывает |
Используя полученные
результаты, получаем:
![]() и
и
![]() — точки строгого минимума функции
— точки строгого минимума функции
![]() ,
,
![]() ,
,
![]() и
и
![]() — точки строгого максимума этой функции.
— точки строгого максимума этой функции.