4.10. Неперервні функції. Властивості неперервних функцій. Неперервність елементарних функцій

Означення. Нехай функція f(x) визначена в деякому повному околі точки x₀(тобто існує f(x₀)). Функція f(x) називається неперервною в точці x₀, якщо вона має границю при x  x₀, і ця границя дорівнює значенню функції в точці x₀: f(x) = f(x₀).

Зауваження. З означення неперервності випливає: якщо відомо, що функція f(x) неперервна в точці x₀, то її границя в цій точці обчислюється просто підстановкою замість x його граничного значення x₀.

Означення. Функція f(x) називається неперервною на проміжку X, якщо вона неперервна в кожній точці цього проміжку.

Графічно неперервність функції означає, що її графік є неперервною лінією.

Властивості неперервних функцій.

1. Якщо функції f(x) і g(x) неперервні в точці x₀, то їх сума f(x) + g(x), добуток f(x)g(x) та частка (при умові, що g(x₀)  0) є функціями, неперервними в точці x₀.

Ця властивість є наслідком означення неперервності і властивості границь 4 а),б) та в).

2. Якщо функція и(x) неперервна в точці x₀, а функція f(x) неперервна в точці и₀ = и(x₀), то складена функція f(и(x)) неперервна в точці x₀.

Ця властивість також випливає з означення неперервності і властивості границь 4 г).

3. Якщо функція f(x) неперервна на відрізку [a,b], то вона обмежена на цьому відрізку.

Цей факт ілюструє рис. 4.4, на якому видно, що множиною значень функції, неперервної на відрізку [a,b], є також відрізок [с,d].

4. Нехай функція f(x) неперервна на відрізку [a,b]. Тоді на цьому відрізку існує точка x₁, в якій функція f(x) приймає своє найменше на відрізку [a,b] значення, і існує точка x₂, в якій функція f(x) приймає своє найбільше на відрізку [a,b] значення.

Н

у

а малюнку 4.4 видно, що найменшим і найбільшим значеннями функції f(x) на відрізку [a,b] є відповідно числа с і d. Але число с є значенням функції f(x) в деякій точці x₁: f(x₁) = с, а число d є значенням функції f(x) в деякій точці x₂: f(x₂) = d, які належать відрізку [a,b].

5

Рис. 4. 4

x^

d

p

O

c

a

x₁

b=x₁

x

y=f(x)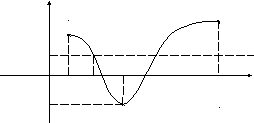

. Функція, неперервна на відрізку, приймає на цьому відрізку всі проміжні значення поміж своїм найменшим і своїм найбільшим значен-нями. Іншими словами для будь-якого числа p, що задовольняє нерівність f(x) < p < f(x), існує принаймні одна точка x^  [a,b] така, що f(x^) = p.

Повернемось до рис. 4.4. Візьмемо довільне число р так, щоб здійснювалась нерівність с < p < d і проведемо пряму у = p. Графік функції – суцільна лінія, розташована між прямими у = с і у = d, тому пряма у = p, що теж лежить між цими прямими, неодмінно перетне графік функції f(x) хоча б в одній точці. Абсциса точки перетину і є x^, бо в цій точці у = f(x^) = р. На рис. 4.4 таких точок навіть дві.

Наслідок. Якщо функція f(x) неперервна на відрізку [a,b] і на його кінцях приймає значення протилежних знаків, то в інтервалі (a,b) є принаймні одна точка x^, в якій f(x^) = 0.

Можна показати, що всі основні елементарні функції (див. п. 4.4) неперервні в своїй області визначення. Тоді з властивостей 1 і 2 неперервних функцій та з означення елементарних функцій (див. п. 4.4) випливає

Теорема (про неперервність елементарних функцій). Усяка елементарна функція неперервна в кожній точці, в якій вона визначена.