
- •Розділ 4. Вступ до математичного аналізу
- •4.1. Поняття множини. Логічна символіка. Необхідна і достатня умови, пряма і обернена теореми
- •4.2. Дійсні числа. Деякі числові множини
- •4.3. Поняття функції. Способи завдання числових функцій
- •4.4. Класифікація функцій. Поняття елементарної функції
- •4.5. Неявна функція, обернена функція, функція, задана параметрично
- •4.6. Границя функції. Нескінченно малі та нескінченно великі функції
- •4.7. Властивості границь
- •4.8. Еквівалентні функції
- •4.9. Визначні границі
- •Друга визначна границя:
- •4.10. Неперервні функції. Властивості неперервних функцій. Неперервність елементарних функцій
- •4.11. Асимптоти графіка функції
4.2. Дійсні числа. Деякі числові множини
Одним з найголовніших об’єктів, які досліджує математика, є величина. Поняття величини настільки широке і всеосяжне, що йому важко дати точне означення. В найпростішому випадку величиною можна вважати те, що, будучи виражене в певних одиницях виміру, характеризується своїм числовим значенням, тобто числом. Математика абстрагується від фізичного чи іншого змісту величини і, говорячи про величини, має на увазі саме їх числові значення. Звідси випливає необхідність розгляду множин, елементами яких є числа – числових множин. Із шкільного курсу відомі такі числові множини, як
-
Множина натуральних чисел =
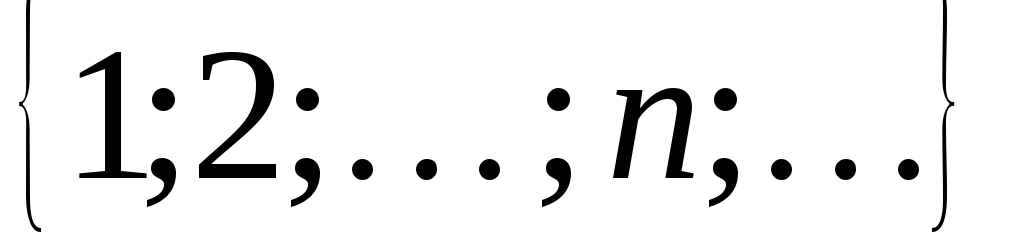 ;
; -
Множина цілих чисел Z =
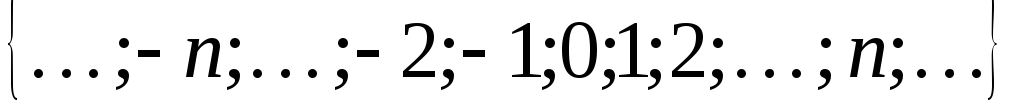 ;
; -
Множина раціональних чисел Q =
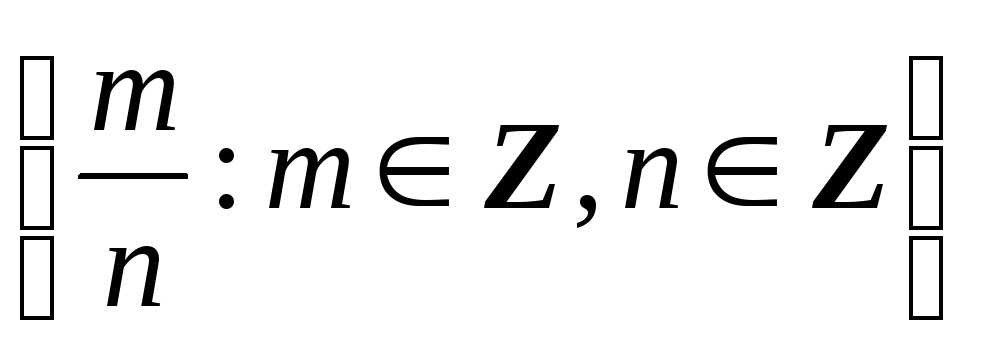 ;
; -
Множина дійсних чисел R =
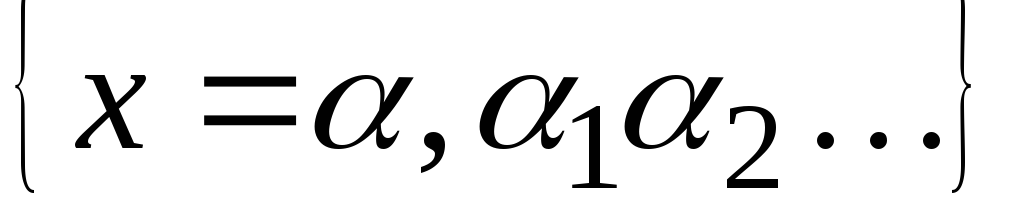 ,
де
,
де
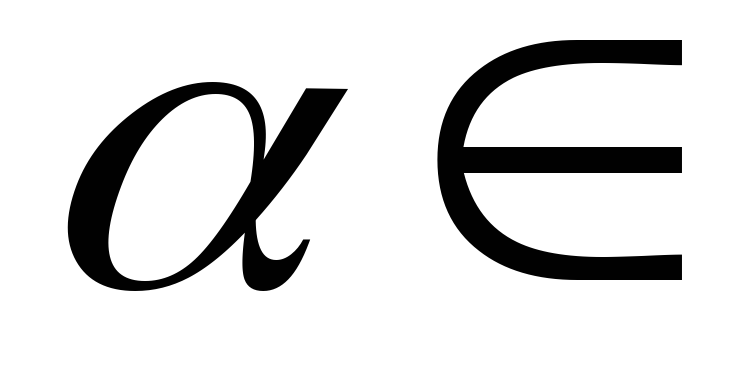 Z,
Z,
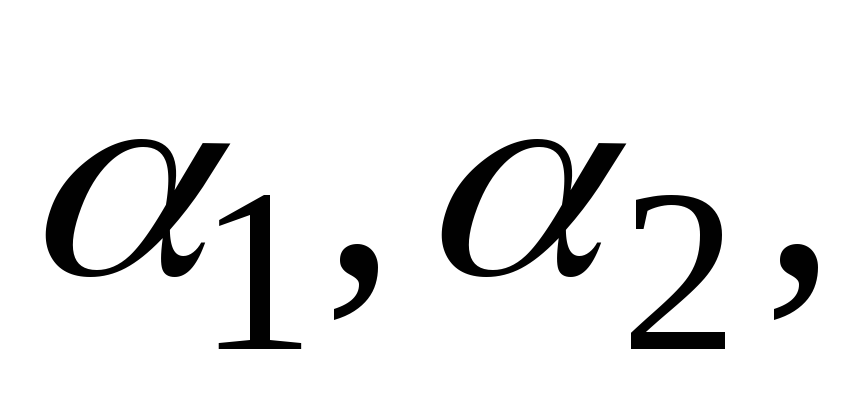 ...
– цифри десяткової системи числення,
тобто
...
– цифри десяткової системи числення,
тобто
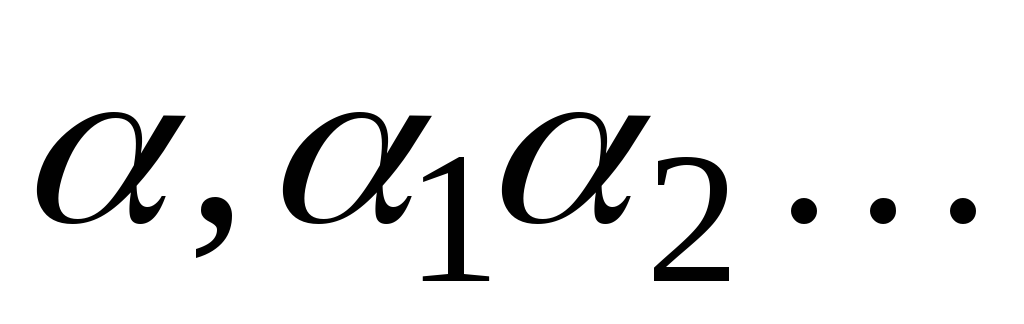 є десятковий дріб (скінчений або
нескінчений).
є десятковий дріб (скінчений або
нескінчений).
Множина дійсних чисел складається з раціональних і ірраціональних чисел. Раціональне число є або цілим числом, або скінченим чи періодичним десятковим дробом. Ірраціональне число – нескінченний неперіодичний дріб. Кожна з перелічених множин містить у собі всі попередні, тобто
Z Q R.
На множині дійсних чисел виконуються дії додавання, віднімання, множення і ділення, правила і властивості яких відомі з курсу середньої школи. Для наочного зображення дійсних чисел користуються числовою прямою або координатною віссю. Кожному числу х R відповідає певна точка числової прямої і, навпаки, кожній точці прямої відповідає певне число. Тому часто замість „число х” кажуть „точка х”.
Найбільш уживаними множинами дійсних чисел є числові проміжки, для яких існують спеціальні позначення і назви:
![]() – відрізок,
або сегмент;
– відрізок,
або сегмент;
![]() – інтервал;
– інтервал;
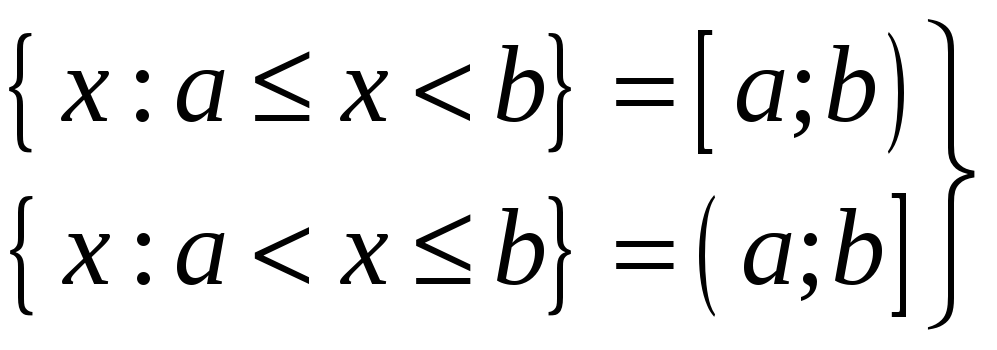 – півінтервали.
– півінтервали.
Тут
![]() і
і
![]() – дійсні числа, при чому
– дійсні числа, при чому
![]() .
Ці числа називають кінцями
відповідних проміжків, а перелічені
проміжки називають скінченними.
В аналізі розглядаються і нескінченні
проміжки:
.
Ці числа називають кінцями
відповідних проміжків, а перелічені
проміжки називають скінченними.
В аналізі розглядаються і нескінченні
проміжки:
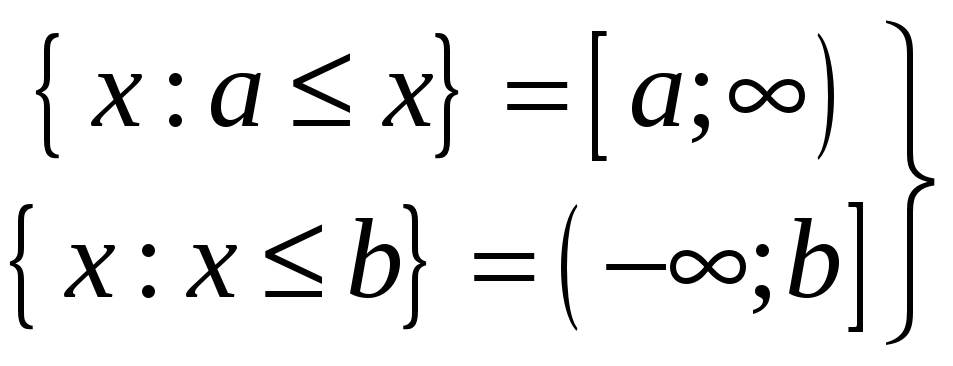 – нескінченні
півінтервали;
– нескінченні
півінтервали;
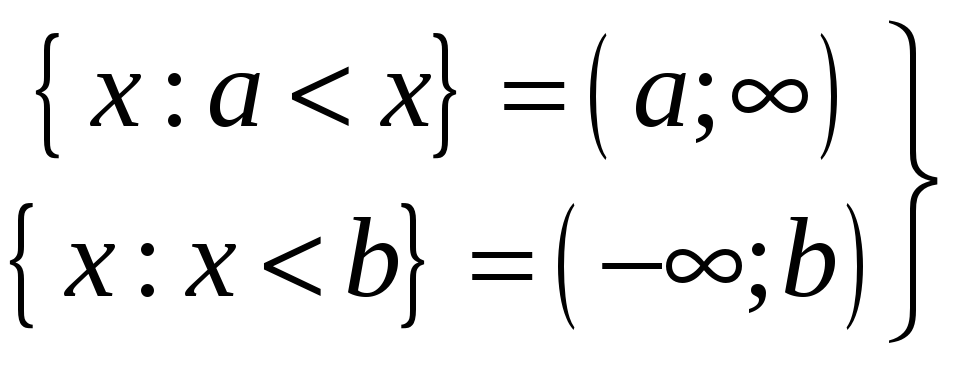 – нескінченні
інтервали.
– нескінченні
інтервали.
Множину
всіх дійсних чисел R
позначають як нескінченний інтервал
![]() .
Слід зазначити, що символ
.
Слід зазначити, що символ
![]() не є числом, і будь-які арифметичні дії
з ним не мають змісту. Числовим проміжкам
природним чином відповідають проміжки
на числовій прямій, так відрізкові
не є числом, і будь-які арифметичні дії
з ним не мають змісту. Числовим проміжкам
природним чином відповідають проміжки
на числовій прямій, так відрізкові
![]() відповідає на числовій прямій відрізок
відповідає на числовій прямій відрізок
![]() такий, що точка
такий, що точка
![]() має координату
має координату
![]() ,
а точка
,
а точка
![]() – координату
– координату
![]() .
Інтервалові
.
Інтервалові
![]() відповідає той самий відрізок, але без
своїх кінцевих точок.
відповідає той самий відрізок, але без
своїх кінцевих точок.
Околом
даної точки
![]() називається будь-який інтервал, що
містить цю точку. Інтервал
називається будь-який інтервал, що
містить цю точку. Інтервал
![]() ,
де
,
де
![]() ,
називається
,
називається
![]() -околом
точки
-околом
точки
![]() і позначається
і позначається
![]() .
Очевидно
.
Очевидно
![]() .
.
Проколеним
околом точки
![]() називається множина всіх точок околу
називається множина всіх точок околу
![]() ,
окрім самої точки
,
окрім самої точки
![]() .
Проколений
.
Проколений
![]() -окіл
точки
-окіл
точки
![]() позначається
позначається
![]() .
.
4.3. Поняття функції. Способи завдання числових функцій
Означення.
Нехай
![]() і
і
![]() – дві не порожні множини. Якщо кожному
елементу
– дві не порожні множини. Якщо кожному
елементу
![]() за певним законом поставлено у
відповідність єдиний елемент
за певним законом поставлено у
відповідність єдиний елемент
![]() ,
то кажуть, що задано відображення
множини
,
то кажуть, що задано відображення
множини
![]() у множину
у множину
![]() ,
або функція,
яка визначена на множині
,
або функція,
яка визначена на множині
![]() і приймає значення із множини
і приймає значення із множини
![]() .
.
Це записують, наприклад, так:
![]() ,
або
,
або
![]() ,
або
,
або
![]() .
.
Тут
літерою
![]() (або якою-небудь іншою) позначено той
закон чи правило, за яким встановлюється
відповідність між х
і у.
Елемент х
називається прообразом,
а елемент у
– його образом.
Множина
(або якою-небудь іншою) позначено той
закон чи правило, за яким встановлюється
відповідність між х
і у.
Елемент х
називається прообразом,
а елемент у
– його образом.
Множина
![]() називається областю
визначення
функції, а множина
називається областю
визначення
функції, а множина
![]() – областю
значень
функції.
– областю
значень
функції.
Серед
способів завдання числових функцій в
математичному аналізі найбільш уживаним
є аналітичний
спосіб, коли функція визначається
аналітичним
виразом
(формулою). Цей вираз вказує, які дії
слід виконати над даним значенням
аргументу, щоб одержати відповідне
значення функції, наприклад:
![]() ,
,
![]() .
Якщо при цьому область визначення
функції не вказується, то під нею
розуміється область
існування аналітичного виразу,
тобто множина всіх дійсних значень
аргументу, для яких аналітичний вираз
має зміст („область припустимих
значень”).
.
Якщо при цьому область визначення
функції не вказується, то під нею
розуміється область
існування аналітичного виразу,
тобто множина всіх дійсних значень
аргументу, для яких аналітичний вираз
має зміст („область припустимих
значень”).
Досить
часто користуються графічним
способом
завдання функції. Графіком
функції
![]() називається множина точок площини, які
мають координати
називається множина точок площини, які
мають координати
![]() .
Отже, якщо задано графік функції, то цим
встановлено відповідність між абсцисами
х
(значенням незалежної змінної) і
ординатами
.
Отже, якщо задано графік функції, то цим
встановлено відповідність між абсцисами
х
(значенням незалежної змінної) і
ординатами
![]() (відповідними значеннями функції).
Графічно визначені функції пов’язані,
зокрема, з наслідками роботи самописних
приладів, таких як осцилограф (реєстрація
змін електричного струму або напруги),
барограф (реєстрація змін атмосферного
тичку), електрокардіограф і т.п. Графіки,
виписані цими приладами задають функції,
властивості яких описують перебіг
відповідних процесів. В математиці
часто виявляється доцільним користуватися
графіками аналітично заданих функцій
для їх геометричного зображення і
унаочнення їх властивостей.
(відповідними значеннями функції).
Графічно визначені функції пов’язані,
зокрема, з наслідками роботи самописних
приладів, таких як осцилограф (реєстрація
змін електричного струму або напруги),
барограф (реєстрація змін атмосферного
тичку), електрокардіограф і т.п. Графіки,
виписані цими приладами задають функції,
властивості яких описують перебіг
відповідних процесів. В математиці
часто виявляється доцільним користуватися
графіками аналітично заданих функцій
для їх геометричного зображення і
унаочнення їх властивостей.
При
табличному
способі
завдання функції обирається певна
множина значень аргументу
![]() і для кожного з них указується відповідне
значення функції
і для кожного з них указується відповідне
значення функції
![]() :
:
|
х |
x1 |
x2 |
… |
xn |
|
y = f(x) |
f(x1) |
f(x2) |
… |
f(xn) |
Табличне завдання функції випливає зокрема як наслідок експерименту, в якому незалежній змінній експериментатор надає певні значення і вимірює відповідні значення функції. Таблиці складають і для функцій, які задані аналітично і часто використовуються, коли безпосереднє обчислення їх значень пов’язане з труднощами (таблиці тригонометричних функцій, логарифмів, тощо). Звичайно, таблиця не може подати всі значення функції. Ті значення функції, які відповідають проміжним значенням аргументу, не включеним до таблиці, можна знайти лише наближено, шляхом інтерполяції.
Сучасне широке поширення електронних обчислювальних пристроїв, від мікрокалькулятора і до суперкомп’ютера, зробило одним із найважливіших способів завдання функції програмний спосіб, коли функцію визначають програмою, за якою обчислювальний пристрій для заданого значення аргументу знаходить відповідне значення функції.
Ми розглянули найбільш уживані способи визначення функцій, але взагалі цих способів може бути безліч, аж до простого словесного опису залежності між змінними.
Приклад.
Так звана функція Діріхле
![]() задана на множині
задана на множині
![]() дійсних чисел, кожному раціональному
числу ставить у відповідність число 1,
а ірраціональному числу – число 0:
дійсних чисел, кожному раціональному
числу ставить у відповідність число 1,
а ірраціональному числу – число 0:
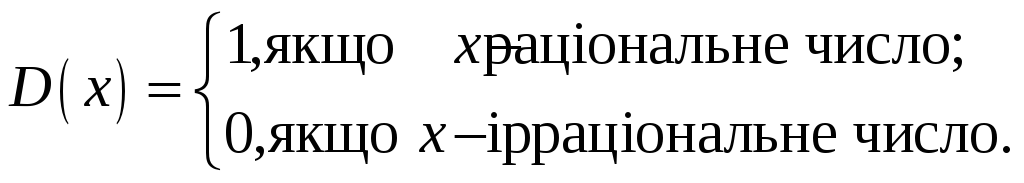
Цим описом функція Діріхле цілком визначена, а от завдати її одним з перелічених вище способів практично неможливо.
Над
функціями визначаються арифметичні
дії.
Нехай функція
![]() визначена на множині
визначена на множині
![]() ,
а функція
,
а функція
![]() визначена на множині
визначена на множині
![]() ,
при чому переріз
,
при чому переріз
![]() .
.
Тоді на
множині Х
визначена сума функцій
![]() ,
так що
,
так що
![]()
![]() .
.
Цілком
аналогічно визначаються різниця
![]() ,
добуток
,
добуток
![]() та частка
та частка
![]() (частка визначена в тих точках множини
Х,
в яких
(частка визначена в тих точках множини
Х,
в яких
![]() ).
).
Якщо
функція
![]() визначена на множині
визначена на множині
![]() і відображає її у множину
і відображає її у множину
![]() ,
а на множині Х
визначена функція
,
а на множині Х
визначена функція
![]() ,
яка відображає множину Х
у множину
,
яка відображає множину Х
у множину
![]() ,
то кожному
,
то кожному
![]() відповідає
відповідає
![]() ,
а кожному
,
а кожному
![]() відповідає певне значення
відповідає певне значення
![]() .
В решті решт ми отримуємо відображення
множини Х
у множину
.
В решті решт ми отримуємо відображення
множини Х
у множину
![]() ,
яке позначається
,
яке позначається
![]() і називається складеною
функцією
від х,
або композицією
функцій
і називається складеною
функцією
від х,
або композицією
функцій
![]() та
та
![]() ,
або функцією
від функції.
При цьому
,
або функцією
від функції.
При цьому
![]() називають проміжним
аргументом
або внутрішньою
функцією,
а
називають проміжним
аргументом
або внутрішньою
функцією,
а
![]() – зовнішньою
функцією.
Так, наприклад,
– зовнішньою
функцією.
Так, наприклад,
![]() є композицією двох функцій
є композицією двох функцій
![]() ,
,
![]() і
і
![]() ,
,
![]() .
Ця композиція відображає множину
.
Ця композиція відображає множину
![]() у множину
у множину
![]() .
.
