
- •Розділ 4. Вступ до математичного аналізу
- •4.1. Поняття множини. Логічна символіка. Необхідна і достатня умови, пряма і обернена теореми
- •4.2. Дійсні числа. Деякі числові множини
- •4.3. Поняття функції. Способи завдання числових функцій
- •4.4. Класифікація функцій. Поняття елементарної функції
- •4.5. Неявна функція, обернена функція, функція, задана параметрично
- •4.6. Границя функції. Нескінченно малі та нескінченно великі функції
- •4.7. Властивості границь
- •4.8. Еквівалентні функції
- •4.9. Визначні границі
- •Друга визначна границя:
- •4.10. Неперервні функції. Властивості неперервних функцій. Неперервність елементарних функцій
- •4.11. Асимптоти графіка функції
4.4. Класифікація функцій. Поняття елементарної функції
Основними елементарними функціями називаються:
-
Стала функція
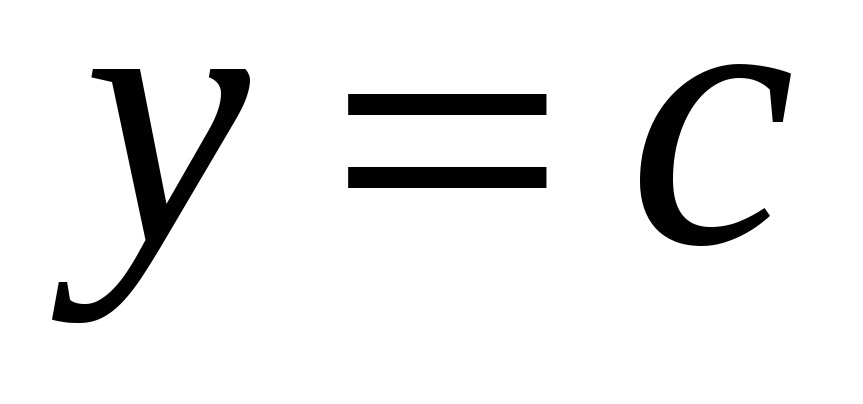
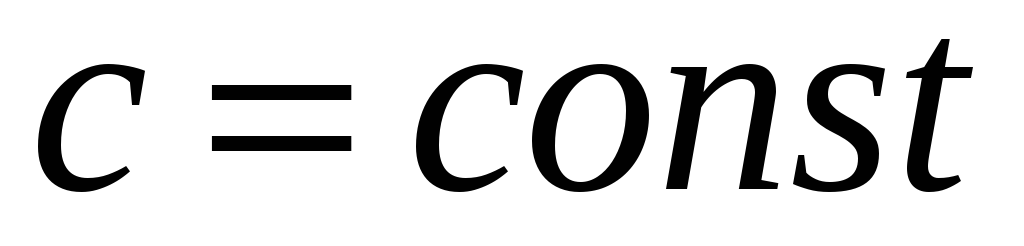 ;
; -
Степенева функція
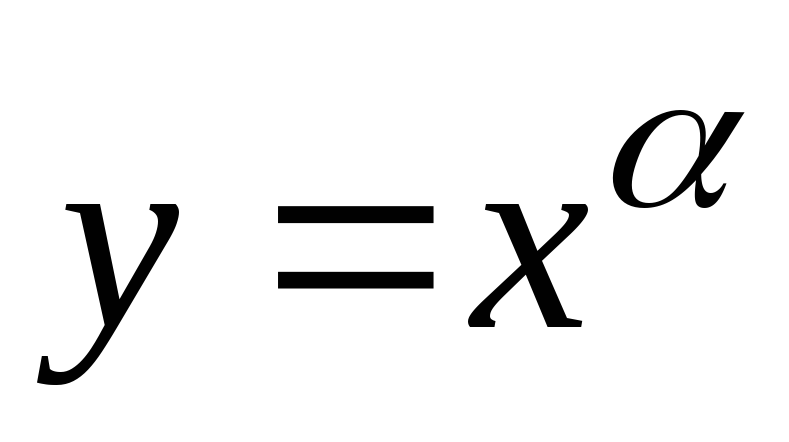 ,
R;
,
R; -
Показникова функція
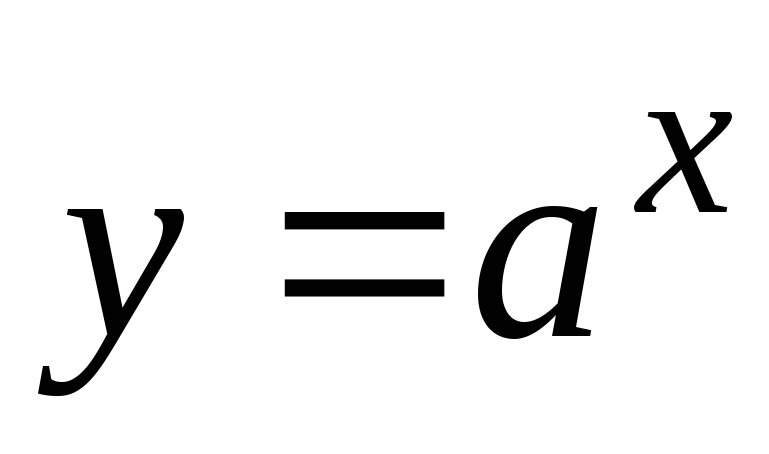
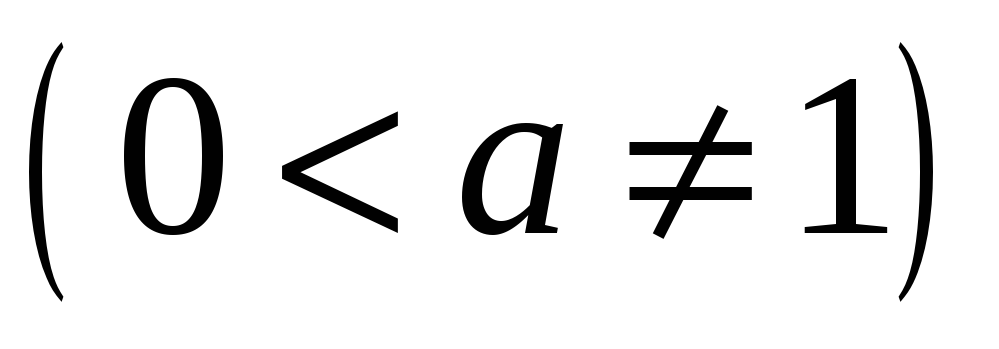 ;
; -
Логарифмічна функція

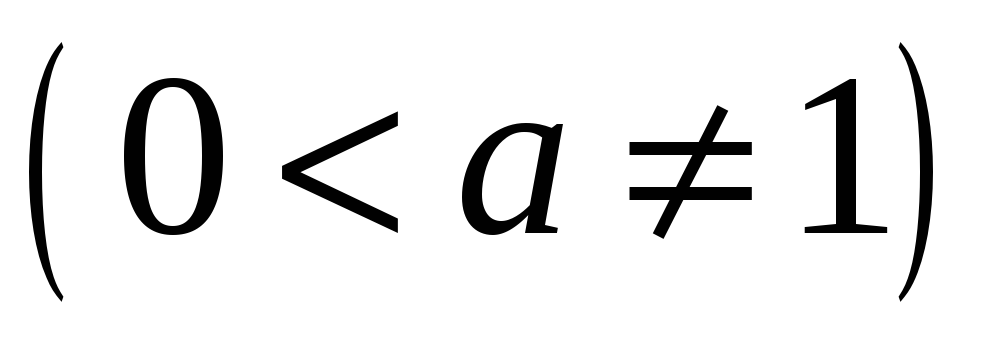 ;
; -
Тригонометричні функції:
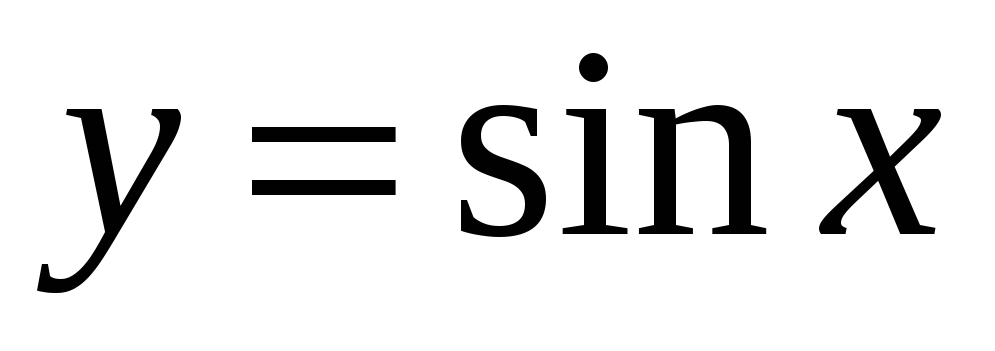 ,
,
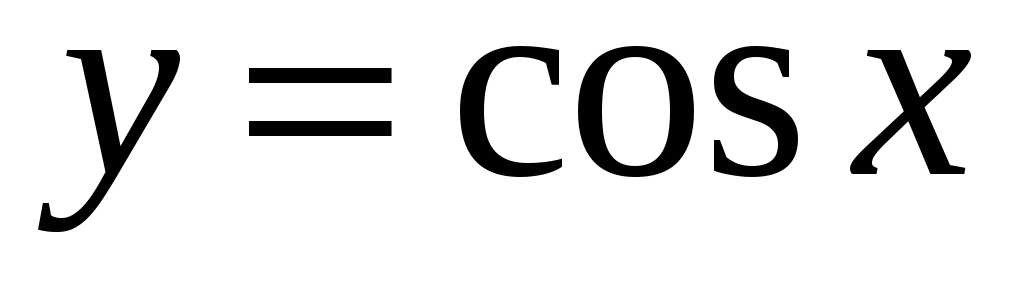 ,
,
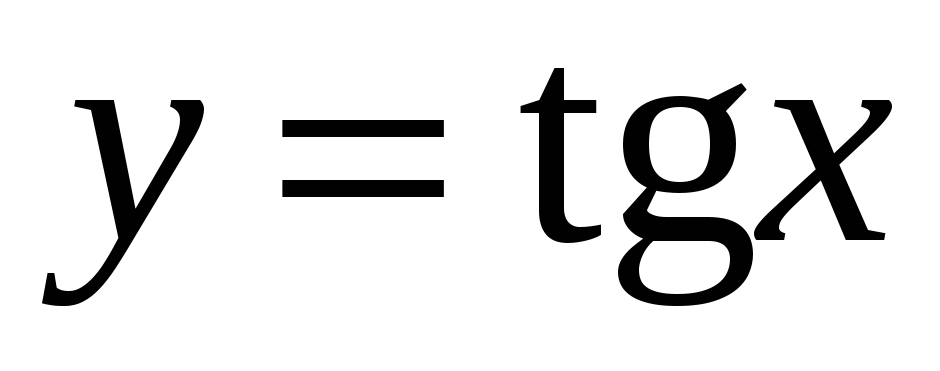 ;
; -
Обернені тригонометричні функції:
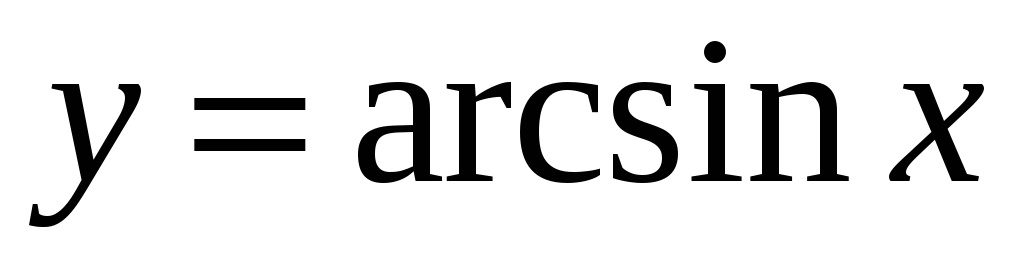 ,
,
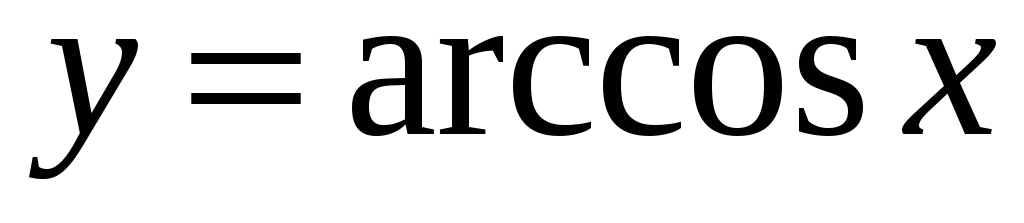 ,
,
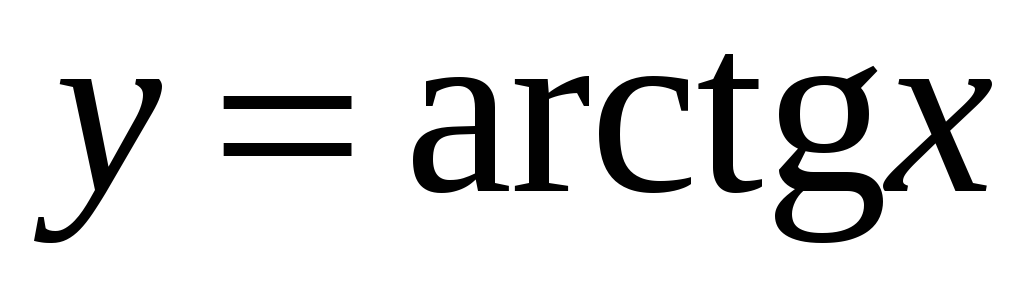 .
.
Функція,
визначена одним аналітичним виразом
(формулою), утвореним з основних
елементарних функцій за допомогою
скінченного числа арифметичних дій і
композицій (утворення складених функцій)
називається елементарною.
Наприклад,
![]() ,
,
![]() ,
тощо.
,
тощо.
Всі інші функції називаються неелементарними. Зокрема, неелементарною є функція, задана різними аналітичними виразами для різних інтервалів зміни аргументу, наприклад
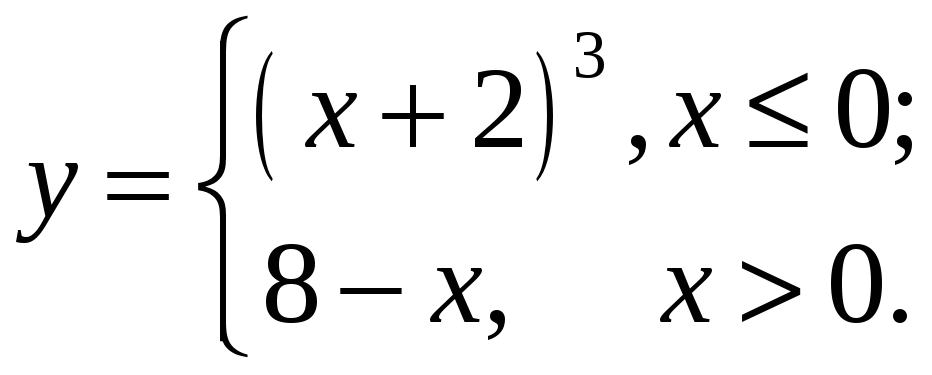
Елементарні функції поділяються на кілька класів.
1. Функція вигляду
![]() ,
,
де п
,
![]() – будь-які числа
– будь-які числа
![]() називається цілою
раціональною функцією
або многочленом
(поліномом)
степеня п.
Многочлен першого степеня називають
також лінійною
функцією,
а многочлен другого степеня – квадратичною
функцією.
називається цілою
раціональною функцією
або многочленом
(поліномом)
степеня п.
Многочлен першого степеня називають
також лінійною
функцією,
а многочлен другого степеня – квадратичною
функцією.
2. Функція, що являє собою відношення двох многочленів
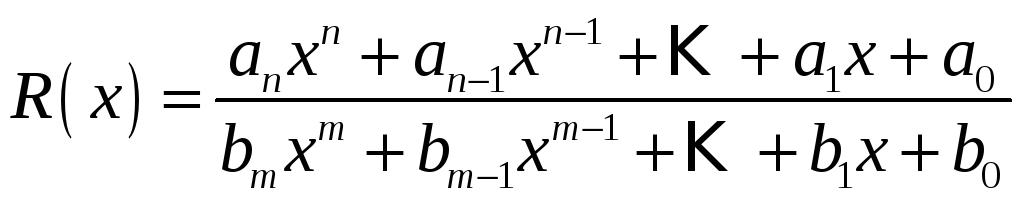 ,
,
називається дробово-раціональною функцією, Многочлен і дробово-раціональні функції разом утворюють клас раціональних функцій.
3. Функція,
яка отримана за допомогою скінченного
числа арифметичних дій і композицій
над степеневими функціями з раціональними
показниками, і не є раціональною,
називається ірраціональною
функцією,
наприклад
![]() ,
,
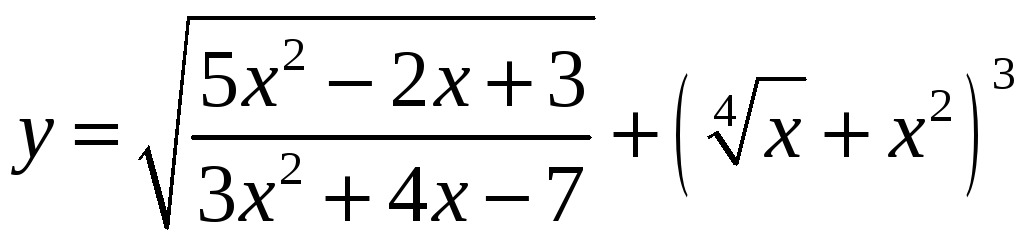 .
.
Раціональні і ірраціональні функції входять до більш загального класу – алгебраїчних функцій, які визначаються рівнянням виду
![]() ,
,
де
![]() є многочленами.
є многочленами.
4. Усяка
функція, яка не є алгебраїчною, називається
трансцендентною.
Це, наприклад, функції
![]() ,
,
![]() ,
,
![]() і т.д.
і т.д.
4.5. Неявна функція, обернена функція, функція, задана параметрично
Досі ми
розглядали функції, задані рівнянням
вигляду
![]() .
В цьому випадку кажуть, що функція
задана явним чином
або є явною.
Але функцію може визначати і рівняння
вигляду
.
В цьому випадку кажуть, що функція
задана явним чином
або є явною.
Але функцію може визначати і рівняння
вигляду
![]() , (4.1)
, (4.1)
не
розв’язане відносно залежної змінної
у.
Тут заданому значенню
![]() незалежної змінної ставиться у
відповідність значення
незалежної змінної ставиться у
відповідність значення
![]() ,
яке є коренем рівняння з одним невідомим
,
яке є коренем рівняння з одним невідомим
![]() .
.
Цей корінь повинен бути єдиним для того, щоб можна було говорити про функцію, задану рівнянням (4.1), інакше даному значенню х відповідатимуть кілька значень у, що суперечить означенню функції. Про функцію, задану рівнянням вигляду (4.1) кажуть, що вона задана неявно або неявною.
Приклади.
1. Рівняння
![]() визначає у
як неявну функцію від х,
тому що кожному значенню х
відповідає єдине значення у,
в чому можна переконатися, розв’язавши
рівняння відносно у
і отримавши явний вираз для у:
визначає у
як неявну функцію від х,
тому що кожному значенню х
відповідає єдине значення у,
в чому можна переконатися, розв’язавши
рівняння відносно у
і отримавши явний вираз для у:
![]() .
.
2.
Тим часом рівняння
![]() не визначає неявної функції, бо, наприклад,
значенню
не визначає неявної функції, бо, наприклад,
значенню
![]() відповідають два значення
відповідають два значення
![]() і
і
![]() .
.
Зазначимо,
що явну функцію
![]() можна завжди записати як неявно задану
рівнянням
можна завжди записати як неявно задану
рівнянням
![]() ,
але не навпаки, тому що не кожне рівняння
вигляду (4.1) можна розв’язати відносно
у.
Слід мати на увазі, що терміни „явна
функція” і „неявна функція” стосуються
не природи функції, а способу її
аналітичного завдання.
,
але не навпаки, тому що не кожне рівняння
вигляду (4.1) можна розв’язати відносно
у.
Слід мати на увазі, що терміни „явна
функція” і „неявна функція” стосуються
не природи функції, а способу її
аналітичного завдання.
Важливою характеристикою функції є монотонність.
Означення.
Розглянемо функцію
![]() ,
визначену в інтервалі
,
визначену в інтервалі
![]() .
Нехай
.
Нехай
![]() і
і
![]() – довільні числа з цього інтервалу.
Якщо з нерівності
– довільні числа з цього інтервалу.
Якщо з нерівності
![]() випливає, що
випливає, що
а)
![]() ,
то функція
,
то функція
![]() називається зростаючою;
називається зростаючою;
б)
![]() ,
то функція
,
то функція
![]() називається неспадною;
називається неспадною;
в)
![]() ,
то функція
,
то функція
![]() називається спадною;
називається спадною;
г)
![]() ,
то функція
,
то функція
![]() називається незростаючою;
називається незростаючою;
Зростаючі,
незростаючі, спадні й неспадні функції
в інтервалі
![]() називаються монотонними
в цьому інтервалі, а зростаючі і спадні
– строго
монотонними.
називаються монотонними
в цьому інтервалі, а зростаючі і спадні
– строго
монотонними.
Нехай
функція
![]() визначена на множині Х,
а множиною її значень є
визначена на множині Х,
а множиною її значень є
![]() .
Це означає, що кожному значенню
.
Це означає, що кожному значенню
![]() відповідає єдине значення
відповідає єдине значення
![]() .
Якщо при цьому різним значенням х
відповідають різні значення у,
то в свою чергу кожному значенню
.
Якщо при цьому різним значенням х
відповідають різні значення у,
то в свою чергу кожному значенню
![]() можна поставити у відповідність єдине
значення
можна поставити у відповідність єдине
значення
![]() ,
таке, що
,
таке, що
![]() .
Таким чином буде визначено функцію
.
Таким чином буде визначено функцію
![]() ,
яка визначена на множині
,
яка визначена на множині
![]() і має множину значень Х.
Ця функція називається оберненою
функцією
до функції
і має множину значень Х.
Ця функція називається оберненою
функцією
до функції
![]() .
Проілюструємо це схемою (рис. 4.1).
.
Проілюструємо це схемою (рис. 4.1).
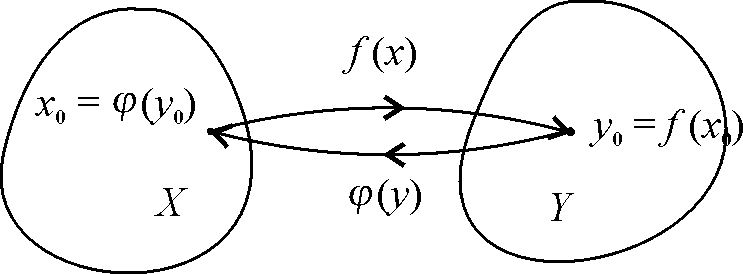
Рис. 4.1
Таким
чином
![]() і
і
![]() ,
тобто функції
,
тобто функції
![]() і
і
![]() є взаємно
оберненими.
Зазначимо, що функцію, обернену до
функції
є взаємно
оберненими.
Зазначимо, що функцію, обернену до
функції
![]() часто позначають як
часто позначають як
![]() .
.
Приклади.
1. Якщо
![]() ,
то
,
то
![]() .
.
Справді,
![]() ;
;
![]() .
.
2. Якщо
![]() ,
то
,
то
![]() ,
бо
,
бо
![]() і
і
![]() .
.
3. Якщо
![]() ,
,
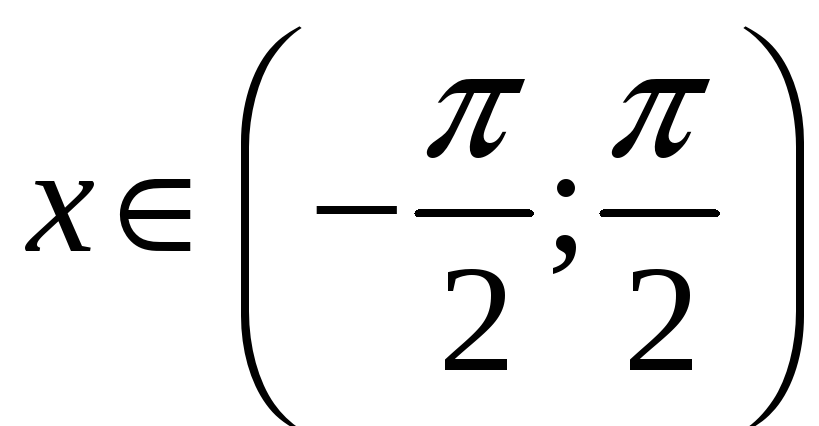 ,
то
,
то
![]() ,
бо
,
бо
![]() і
і
![]() .
.
Теорема
Якщо функція
![]() строго монотонна в інтервалі
строго монотонна в інтервалі
![]() ,
то вона має обернену.
,
то вона має обернену.
Дійсно, з означення строго монотонної функції випливає, що різним значенням аргументу ставляться у відповідність різні значення функції, а це внаслідок визначення оберненої функції і означає її наявність.
В розділі 3 йшла мова про те, що лінія на площині може бути задана параметричними рівняннями вигляду
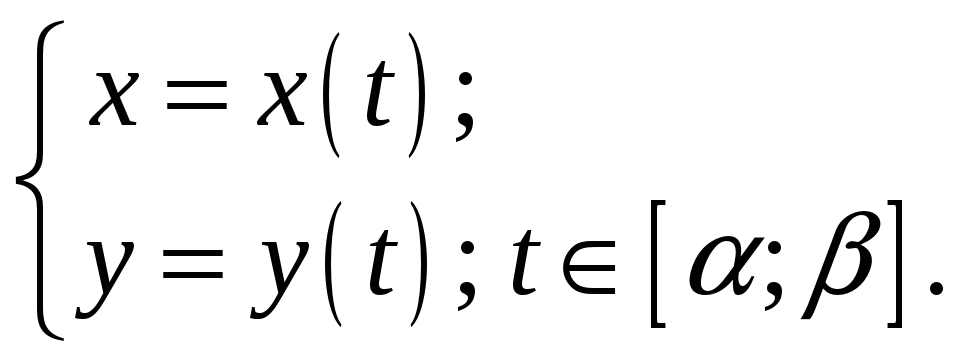 (3.5)
(3.5)
Нехай
![]() – яке-небудь число з проміжку
– яке-небудь число з проміжку
![]() .
Тоді
.
Тоді
![]() і
і
![]() ,
тобто рівняння (3.5)
ставлять у відповідність кожному числу
,
тобто рівняння (3.5)
ставлять у відповідність кожному числу
![]() із області значень функції
із області значень функції
![]() одне або кілька значень у
із області значень функції
одне або кілька значень у
із області значень функції
![]() .
Якщо при цьому кожному
.
Якщо при цьому кожному
![]() відповідає єдине значення
відповідає єдине значення
![]() ,
то це означає, що рівняння (3.5)
визначають функцію
,
то це означає, що рівняння (3.5)
визначають функцію
![]() із областю визначення
із областю визначення
![]() і областю значень
і областю значень
![]() .
Такий спосіб завдання функції
.
Такий спосіб завдання функції
![]() називається параметричним.
Рівняння (3.5)
визначають деяку криву на площині, отже
і задана параметрично функція визначає
на площині криву, а саме графік цієї
функції, але не всяка параметрично
задана лінія визначає функцію. Кожному
значенню
називається параметричним.
Рівняння (3.5)
визначають деяку криву на площині, отже
і задана параметрично функція визначає
на площині криву, а саме графік цієї
функції, але не всяка параметрично
задана лінія визначає функцію. Кожному
значенню
![]() повинно відповідати єдине значення
повинно відповідати єдине значення
![]() ,
а це можливо, якщо кожному значенню
,
а це можливо, якщо кожному значенню
![]() відповідає єдине значення х,
тобто якщо функція
відповідає єдине значення х,
тобто якщо функція
![]() має обернену
має обернену
![]() .
Якщо ця обернена функція відома, то
можна одержати явний вираз функції
.
Якщо ця обернена функція відома, то
можна одержати явний вираз функції
![]() як складеної функції
як складеної функції
![]() .
.
Приклади.
-
Рівняння
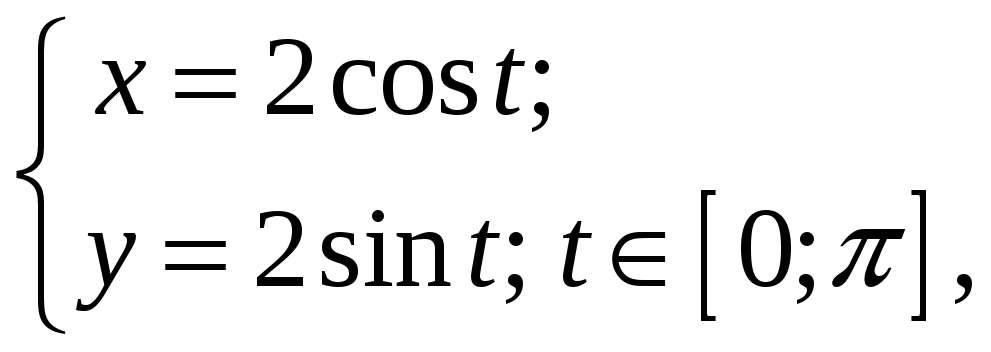
визначають
функцію, оскільки змінна
![]() строго монотонна на відрізку
строго монотонна на відрізку
![]() ,
отже має обернену, а саме
,
отже має обернену, а саме
![]() .
Тоді явний вираз функції
.
Тоді явний вираз функції
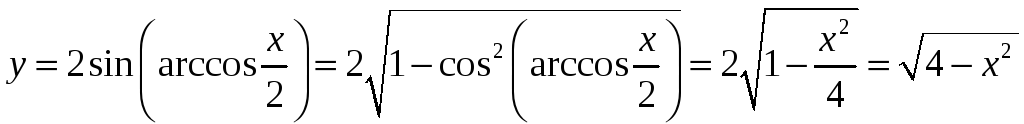 .
.
Таким
чином задана функція має графіком
півколо
![]() ,
розташоване у верхній півплощині, тому
що при
,
розташоване у верхній півплощині, тому
що при
![]() значення
значення
![]() .
.
2. Рівняння
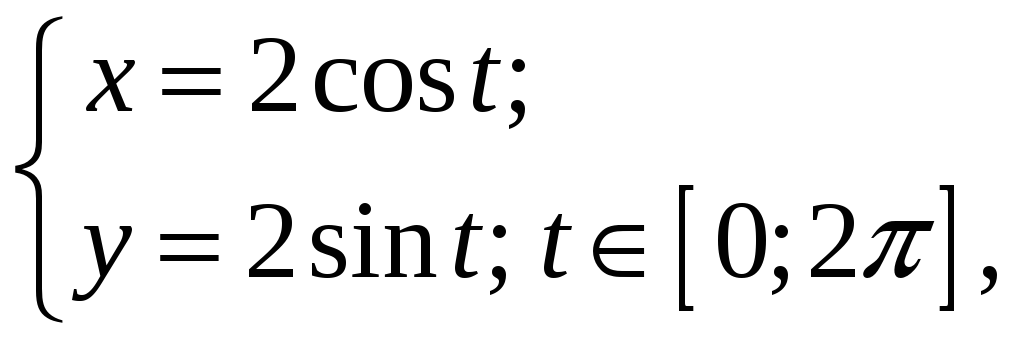
визначають
на площині коло
![]() ,
але функцію не визначають. Справді,
наприклад,
,
але функцію не визначають. Справді,
наприклад,
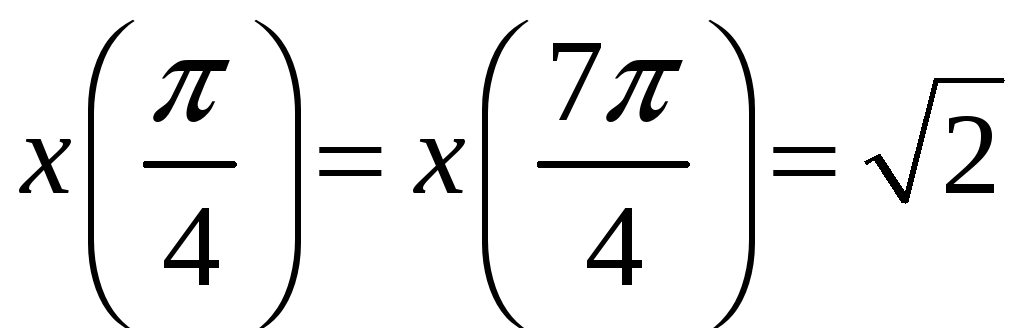 ,
тоді як
,
тоді як
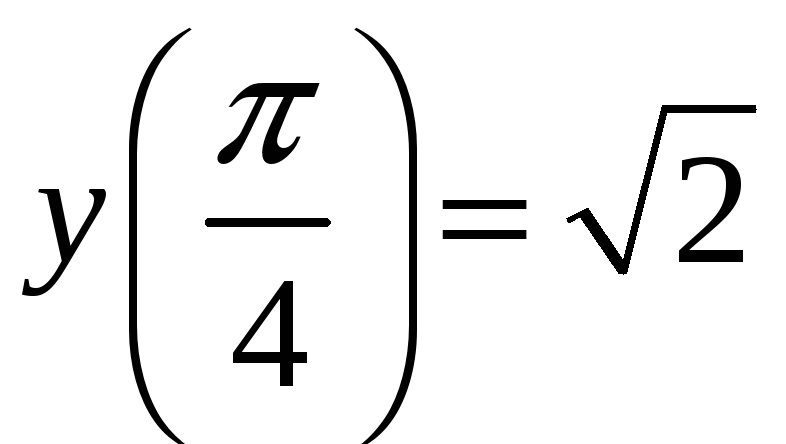 ,
а
,
а
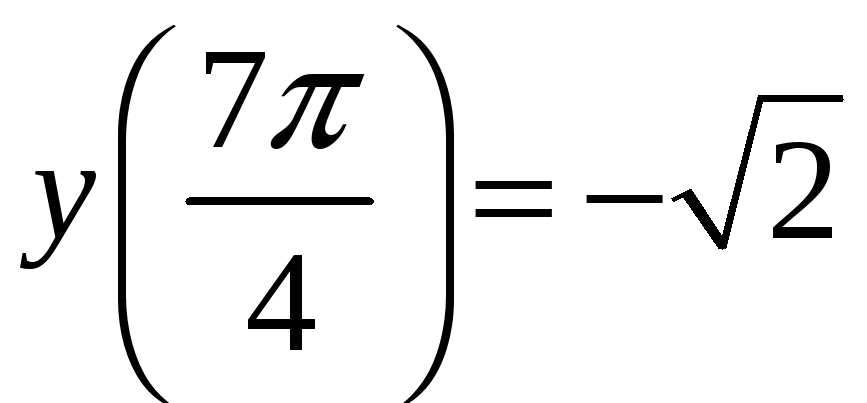 .
.
Зауважимо, що явне чи параметричне визначення функції характеризують не природу функції, а лише спосіб її аналітичного завдання.
