
- •Розділ 4. Вступ до математичного аналізу
- •4.1. Поняття множини. Логічна символіка. Необхідна і достатня умови, пряма і обернена теореми
- •4.2. Дійсні числа. Деякі числові множини
- •4.3. Поняття функції. Способи завдання числових функцій
- •4.4. Класифікація функцій. Поняття елементарної функції
- •4.5. Неявна функція, обернена функція, функція, задана параметрично
- •4.6. Границя функції. Нескінченно малі та нескінченно великі функції
- •4.7. Властивості границь
- •4.8. Еквівалентні функції
- •4.9. Визначні границі
- •Друга визначна границя:
- •4.10. Неперервні функції. Властивості неперервних функцій. Неперервність елементарних функцій
- •4.11. Асимптоти графіка функції
4.8. Еквівалентні функції
Означення. Функції f(x) і g(x) називають еквівалентними у точці x0 (або еквівалентними на нескінченності) і пишуть f(x) g(x), x x0 (x ), якщо
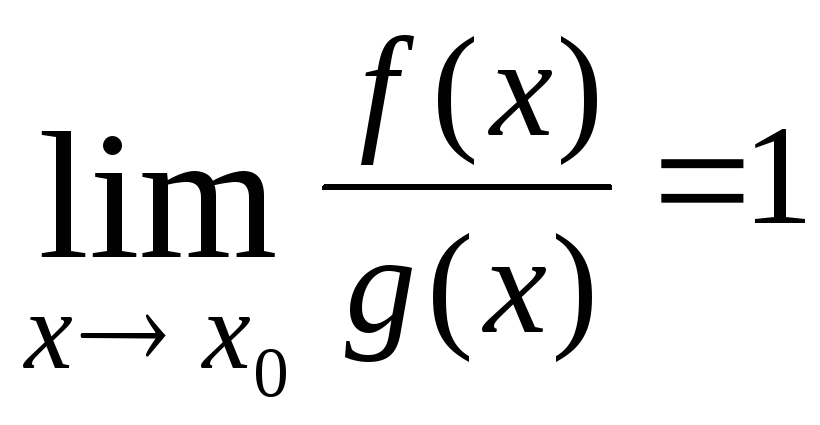
 . (4.2)
. (4.2)
Приклад.
Доведемо,
що многочлен
![]() еквівалентний на нескінченності своєму
доданку, що містить найвищий степінь
х:
еквівалентний на нескінченності своєму
доданку, що містить найвищий степінь
х:
![]()
![]() при x
. (4.3)
при x
. (4.3)
Розглянемо границю
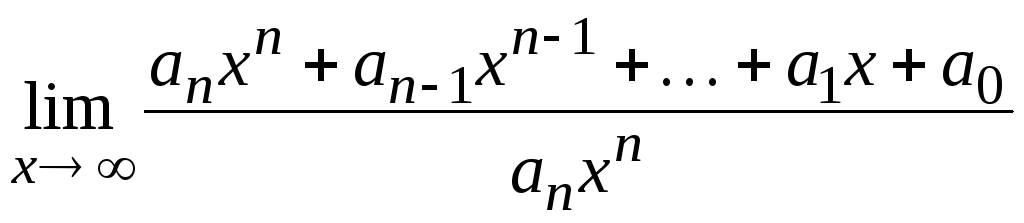 = =
= =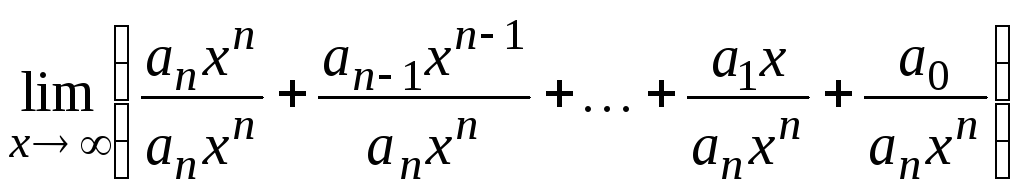 =
=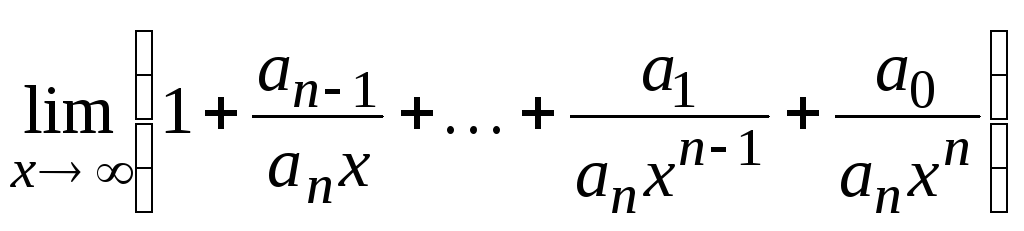 ==
==![]() 1
+
1
+
![]() + … +
+ … +
![]() +
+
![]() .
.
Функції
виду
![]() ,
0, є нескінченно великими при
x
,
отже функції
,
0, є нескінченно великими при
x
,
отже функції
![]() є нескінченно малими і
є нескінченно малими і
![]() .
Таким чином,
.
Таким чином,
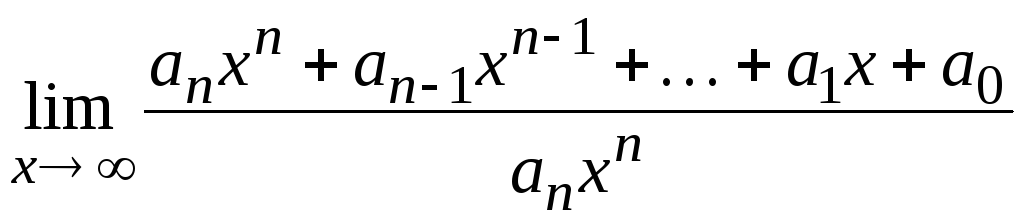 = 1,
= 1,
і згідно
з означенням еквівалентних функцій
(4.2)
![]()
![]() при x
.
при x
.
Теорема (властивість еквівалентних функцій). Якщо f(x) і g(x) – еквівалентні функції в точці x0, то
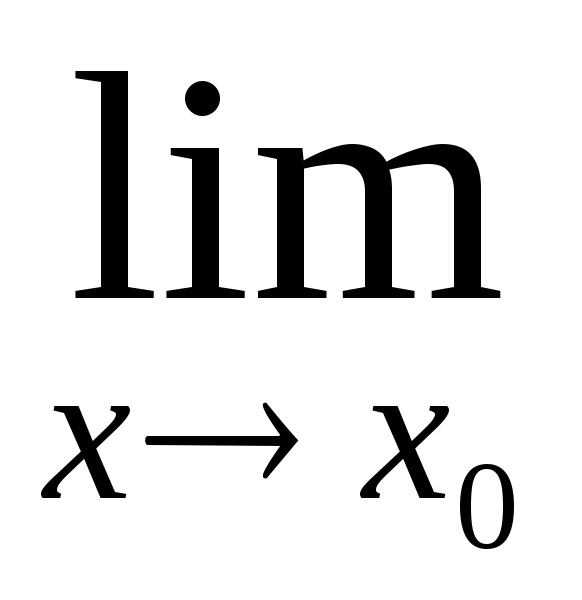 (f(x)h(x))
=
(f(x)h(x))
=
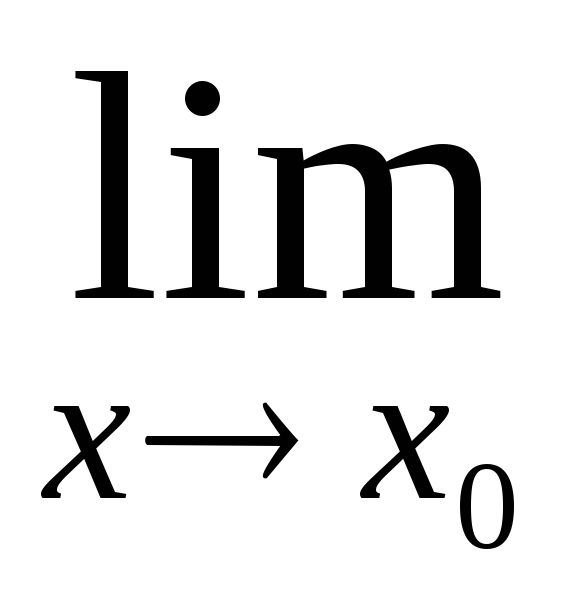 (g(x)h(x))
і
(g(x)h(x))
і
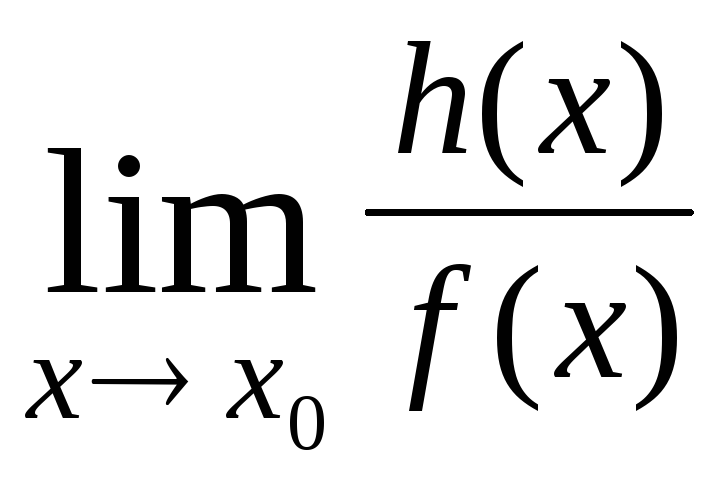 =
= , (4.4)
, (4.4)
якщо існує границя в одній з частин рівності.
Доведення. Нехай, наприклад, існують границі в правих частинах рівностей (4.4). Тоді
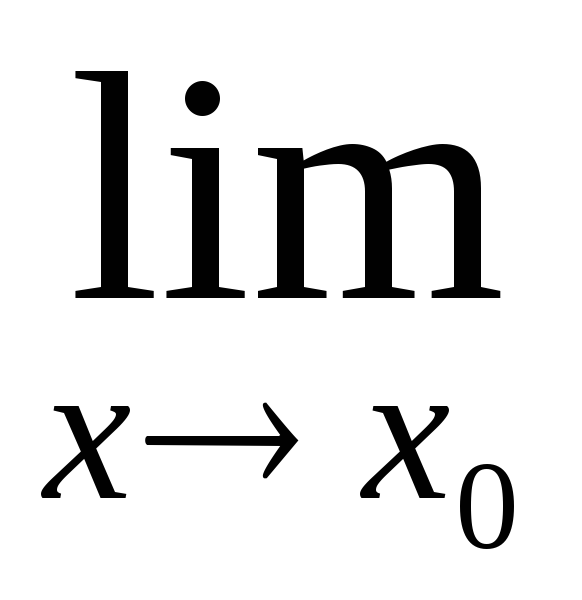 (f(x)h(x))
=
(f(x)h(x))
=
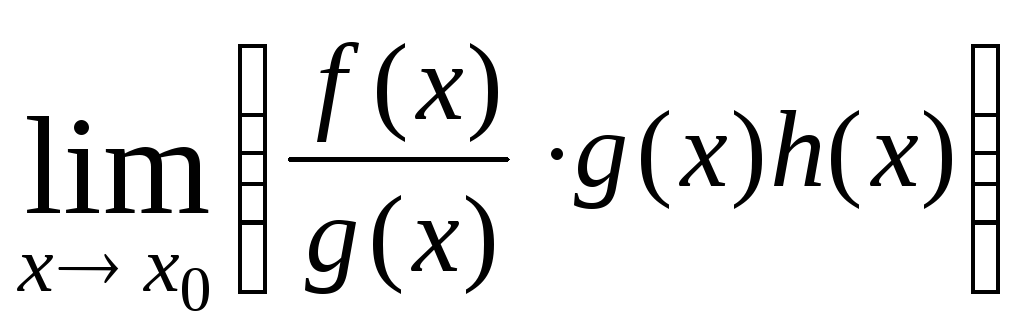 =
=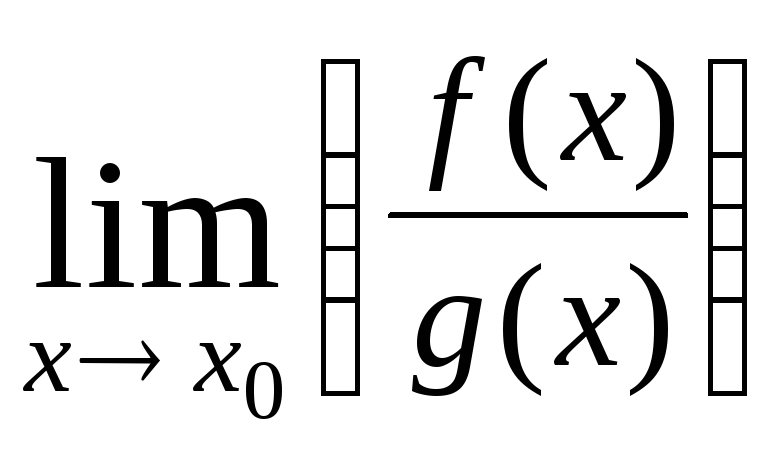 ·
· (g(x)h(x))
= =1·
(g(x)h(x))
= =1·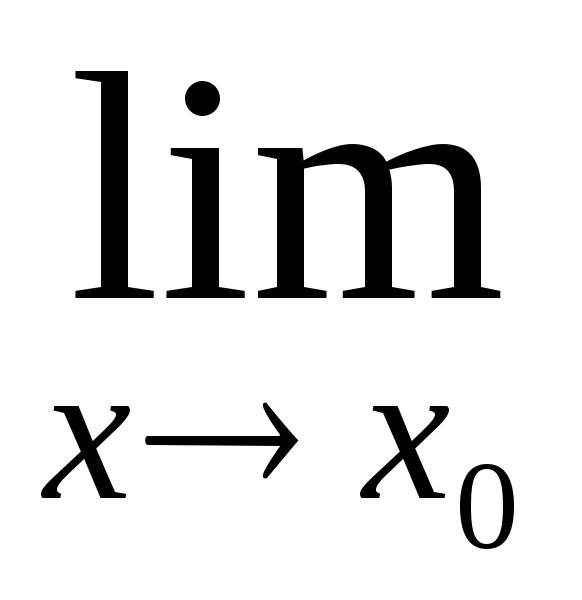 (g(x)h(x));
(g(x)h(x));
 =
=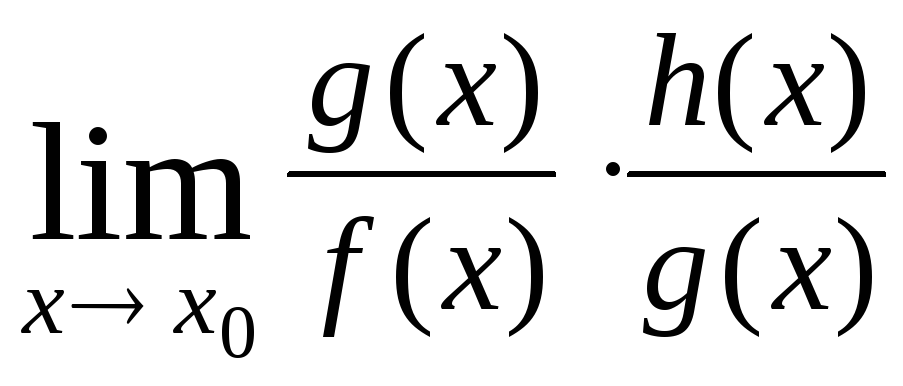 =
=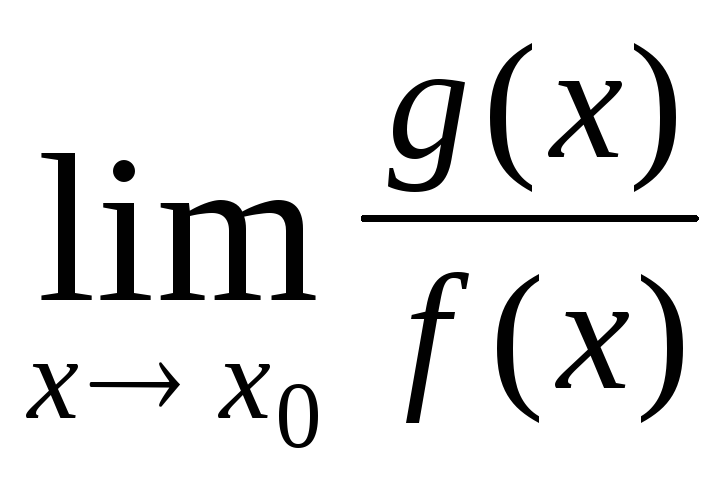 ·
·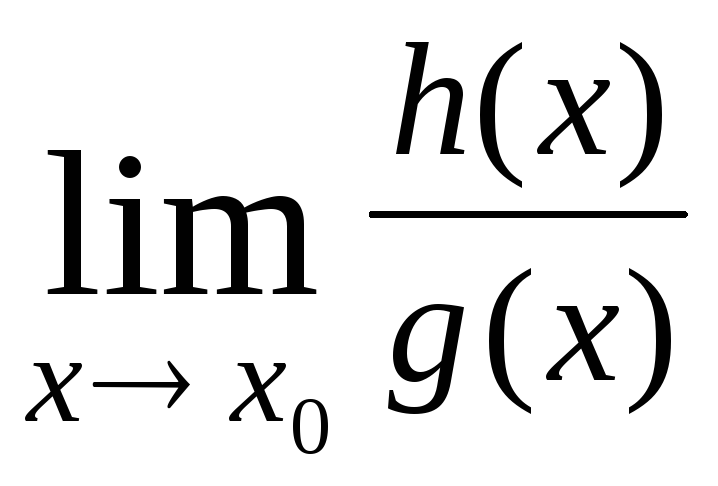 =1·
=1·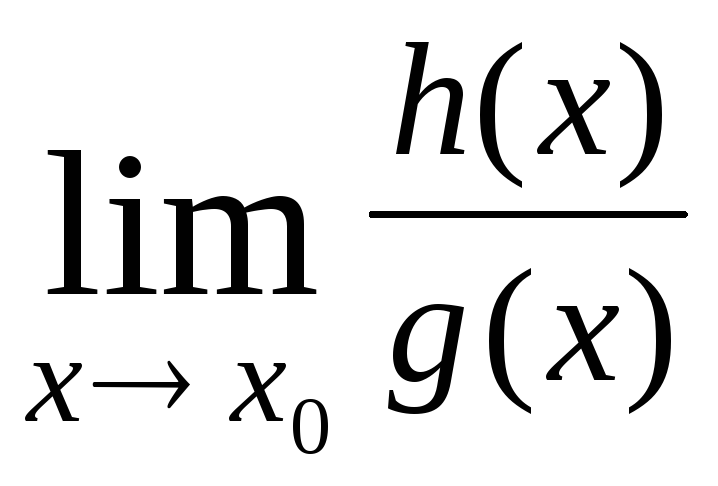 .
.
Цілком аналогічно проходить доведення для випадку, коли існують границі в лівих частинах рівностей (4.4).
Приклад. Знайти границі
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Розв'язання.
При
розв’язанні цих прикладів ми не можемо
скористатись властивістю границь 4 в),
тому що і чисельник, і знаменник дробів
є нескінченно великими функціями, тобто
не мають границі. В такому випадку
говорять, що це невизначеність виду
![]() .
Скористаємось рівностями (4.4) та
еквівалентністю (4.3). Замінимо чисельник
та знаменник кожного дробу на еквівалентну
функцію:
.
Скористаємось рівностями (4.4) та
еквівалентністю (4.3). Замінимо чисельник
та знаменник кожного дробу на еквівалентну
функцію:
а)
![]() =
=
![]() =
=
![]() ;
;
б)
![]() =
=
![]() =
=
![]() ,
бо
функція
,
бо
функція
![]() є нескінченно великою при x
;
є нескінченно великою при x
;
в)
![]() =
=
![]() =
=
![]() =
0,
оскільки
функція
=
0,
оскільки
функція
![]() є нескінченно малою при x
.
є нескінченно малою при x
.
4.9. Визначні границі
-
Перша визначна границя – це границя
![]() . (4.5)
. (4.5)
Доведення. Зауважимо, що при обчисленні цієї границі не можна скористатись властивістю 4 в) границь, тому що границя знаменника дорівнює нулю.
Рис. 4. 3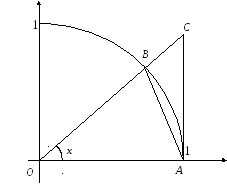
![]() .
Знайдемо площі трикутників АОВ
і АОС
та сектора АОВ.
.
Знайдемо площі трикутників АОВ
і АОС
та сектора АОВ.
SAOB
=
![]() ;
;
SAOC
=
![]() ;
;
Sсектора
AOB
=
![]() .
.
За малюнком SAOB < Sсектора AOB < SAOC, отже
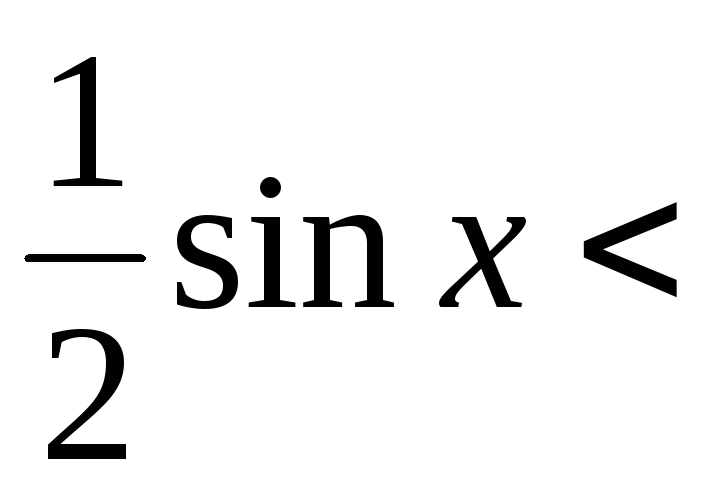
![]()
![]() .
.
Оскільки
sin
x
> 0
при x
( 0;
![]() ,
можемо розділити ці нерівності почленно
на
,
можемо розділити ці нерівності почленно
на
![]() .
Одержимо
.
Одержимо
![]() або
або
![]() .
.
Через
парність функцій
![]() і
і
![]() ці нерівності зберігаються і при x
(–
ці нерівності зберігаються і при x
(–![]() ;
0). При цьому
;
0). При цьому
![]() і за властивістю 6 виходить, що
і за властивістю 6 виходить, що
![]() .
.
Наслідки.
1.
![]() ;
;
2.
![]() ;
;
3.
![]() .
.
Таким чином, згідно з означенням еквівалентних функцій (4.2), при x 0
sinx x;
tgx x;
arcsinx x;
arctgx x.
Очевидно, що всі ці співвідношення залишаться в силі, якщо замінити в них x на яку-небудь нескінченно малу функцію.
Приклад.
Обчислити
![]() .
.
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() .
.
-
Друга визначна границя:
![]() , (4.6)
, (4.6)
де е 2, 718 – стала Ейлера.
Наслідок. Нехай (x) – нескінченно мала функція, а (x) – нескінченно велика при x x0. Тоді
![]() . (4.7)
. (4.7)
Доведення. Зрозуміло, що рівність (4.6) збережеться, якщо замінити x на будь-яку нескінченно велику функцію. Зробимо деякі арифметичні перетворення:
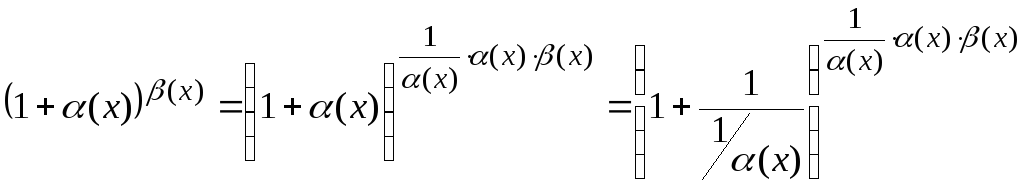 .
.
Оскільки
(x)
–
нескінченно
мала
функція,
то
![]() –
нескінченно
велика
при x
x0.
Таким чином,
–
нескінченно
велика
при x
x0.
Таким чином,

е
при x
x0.
Звідси і виходить рівність (4.7).
е
при x
x0.
Звідси і виходить рівність (4.7).
Приклад.
Обчислити
![]() .
.
Розв'язання.
Тут
згідно
з еквівалентністю (4.3)
![]() ,
а покажчик степеня нескінченно великий
при x
,
тобто маємо невизначеність типу
,
а покажчик степеня нескінченно великий
при x
,
тобто маємо невизначеність типу
![]() .
Саме такого характеру невизначеність
у виразі (4.6). Щоб скористатись наслідком
(4.7), перетворимо заданий вираз, виділивши
в дужках одиницю:
.
Саме такого характеру невизначеність
у виразі (4.6). Щоб скористатись наслідком
(4.7), перетворимо заданий вираз, виділивши
в дужках одиницю:
![]() =
=
![]() =
=
![]() =
=
=
=![]() =
=
![]() =
=
![]() =
=
![]() .
.
