34. Гармонические колебания и их характеристики.

Колебания – это движения или процессы, которые характеризуются определенной повторяемостью во времени.

Гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса.

35. Дифференциальное уравнение свободных незатухающих гармонических колебаний и его решение.

Уравнение гармонических колебаний

Запишем первую и вторую производную по времени от величины S (скорость и ускорение).

– дифференциальное уравнение гармонических колебаний

Решением этого уравнения является:

Изображение гармонических колебаний графически:

Другое представление колеблющейся величины – комплексным числом:

– действительная часть

36. Пружинный, физический и математический маятники.

Пружинный маятник

Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы.

– дифференциальное уравнение гармонического колебания

Физический маятник

Физический маятник – это твёрдое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс тела.

– дифференциальное уравнение для колебаний физического маятника

Математический маятник

Математический маятник – это материальная точка массой m, подвешенная на нерастяжимой невесомой нити и колеблющаяся под действием силы тяжести. (Это частный случай физического маятника).

– дифференциальное уравнение для математического маятника

37. Гармонический осциллятор. Энергия гармонического осциллятора.

Гармонический осциллятор – система, совершающая колебания, описываемые уравнением .

Примерами гармонического осциллятора служат: пружинный, физический, математический маятники.

Полная энергия колеблющейся точки

Пусть точка совершает гармонические колебания по закону

Кинетическая энергия:

Потенциальная энергия:

Полная энергия

Закон сохранения энергии справедлив.

38. Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. Добротность колебательной системы.

Свободные гармонические колебания в колебательном контуре

Колебательный контур – цепь, состоящая из последовательно соединенных конденсатора, катушки и резистора.

Идеализированный контур – контур, в котором сопротивление пренебрежимо мало.

В промежуточные моменты времени энергия определяется как:

(из ЗСЭ)

(L-C-R)

– дифференциальное уравнение колебаний заряда в реальном колебательном контуре

– формула Томпсона

Решением дифференциального уравнения идеализированного контура является

Колебания тока опережают по фазе колебания заряда на .

Дифференциальное уравнение свободных затухающих колебаний

Затухающие колебания – колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается.

Запишем дифференциальное уравнение свободных затухающих колебаний.

S – колеблющаяся величина

– коэффициент затухания

– циклическая частота свободных незатухающих колебаний, т. е. при .

Решение ищем в ви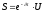де:

, где

Амплитуда таких колебаний уменьшается по экспоненциальному закону.

– период затухающих колебаний

Для характеристики колебательной системы пользуются понятием добротности Q:

Для колебательного контура:

– дифференциальное уравнение затухающих колебаний в R-L-C контуре

– решение дифференциального уравнения

– добротность колебательной системы