- •8. Преобразование матрицы линейного оператора при переходе к новому базису.
- •9.Собственные значения и собственные вектора линейных операторов:
- •10. Свойства собственных значений и собственных векторов линейного оператора.
- •11.Квадратичные формы. Определение. Примеры.
- •12. Преобразование квадратичной формы к каноническому виду.
- •13. Приведение к каноническому виду уравнений кривых и поверхностей 2-го порядка:
- •14.Каноническое уравнение кривых и поверхностей II порядка (см.Реферат)
- •15.Дифференцильные уравнения (основные понятия, примеры)
- •16.Ду I порядка. Задача Коши.
- •17.Уравнение, с разделяющимися переменными.
- •18. Однородные уравнения I порядка.
- •19.Линейные уравнения первого порядка.
- •24.Однородные дифференциальные уравнения с постоянными коэффициентами.
- •25. Линейные неоднородные уравнения с постоянными коэффициентами:
- •26. Метод вариаций произвольных постоянных.
- •27. Линейные ду высших порядков
- •28.Вронскиан, его свойства.
- •29.Преобразования Лапласа.
- •30.Свойства преобразований Лапласа
- •35.Решение систем дифференциальных уравнений операционным методом.
24.Однородные дифференциальные уравнения с постоянными коэффициентами.
Уравнение вида
![]() -
линейное ДУ с постоянными коэффициентами.
-
линейное ДУ с постоянными коэффициентами.
Если
![]() ,
то уравнение однородное.
,
то уравнение однородное.
Решение этого уравнения ищем в виде
![]() ,
где k=const.
,
где k=const.
![]()
![]()
![]()
![]()
![]() - характеристическое уравнение
- характеристическое уравнение
![]()
1)![]() >0
>0
![]() - 2 действ., разл. корня.
- 2 действ., разл. корня.
![]()
2)
![]() =0
=0
![]() =
=![]() =
=![]()
![]()
3)
![]() <0
<0 ![]() ,
,
![]()
![]()
25. Линейные неоднородные уравнения с постоянными коэффициентами:
![]() (1)
(1)
Общим решением неоднородных уравнений вида (1) = сумме общих решений, соотв. однородным уравнениям и частных решений неоднородных уравнений.
![]() ,
где
,
где
![]() -
общее решение
-
общее решение
![]() ,
z(x)- частное
решение (1).
,
z(x)- частное
решение (1).
Метод неопределенных коэффициентов:
1)![]() ,
,
![]() ,
,
![]()
![]()
![]()
Если m- корень характ
уравнения, то
![]()
2)
![]() ,
,
![]()
![]()
![]() ,
находим А и В
,
находим А и В
3)
![]()
![]()
![]()
![]()
![]()
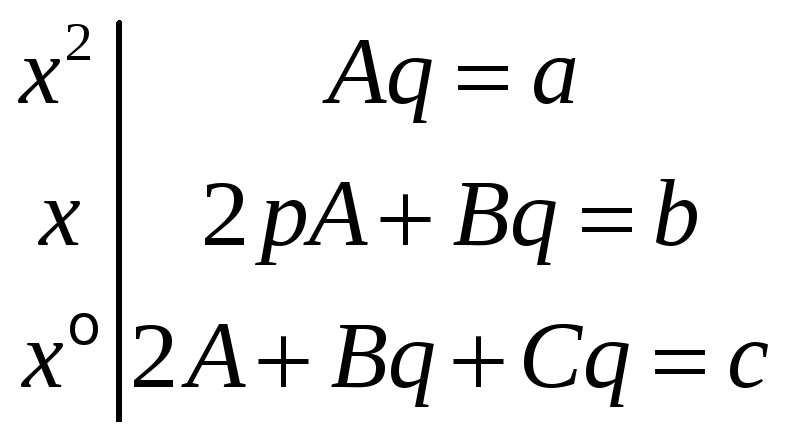
4)
![]()
![]()
![]()
![]()
![]()
Если
![]() -корень
хар уравнения, след.
-корень
хар уравнения, след.
![]()
Если
![]() и
и
![]() -корни
(кратности 2), то
-корни
(кратности 2), то
![]()
5)
![]() ,
где
,
где
![]() -
1 вид,
-
1 вид,
![]() -2
вид., след.
-2
вид., след.
![]()
26. Метод вариаций произвольных постоянных.
![]() (1)
(1)
![]() 1) z ищем методом вариаций.
1) z ищем методом вариаций.
![]() ,
где
,
где
![]() и
и
![]() -
произвольные постоянные
-
произвольные постоянные
2) Пусть
![]() и
и
![]() ,
то есть это функции, которые подберем
так, чтобы
,
то есть это функции, которые подберем
так, чтобы
![]() было решением уравнения (1)
было решением уравнения (1)
![]() (2)
(2)
Подберем
![]() и
и
![]() так, чтобы сумма
так, чтобы сумма
![]() ,
тогда:
,
тогда:
![]()
![]()
Так как z- решение (1), то подставим это в уравнение (1)
![]()
![]()
 (3)
(3)
Систему (**) относительно 2-х неизвестных
![]() и
и
![]() решаем по Крамеру:
решаем по Крамеру:
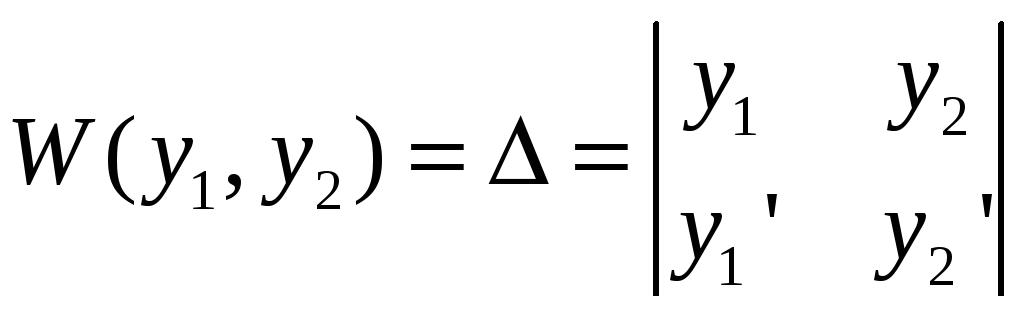
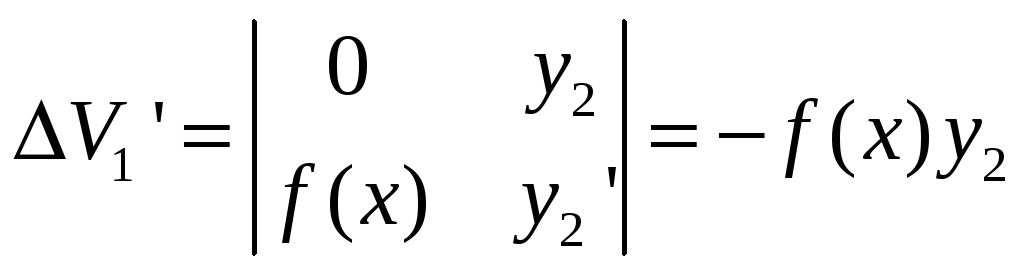
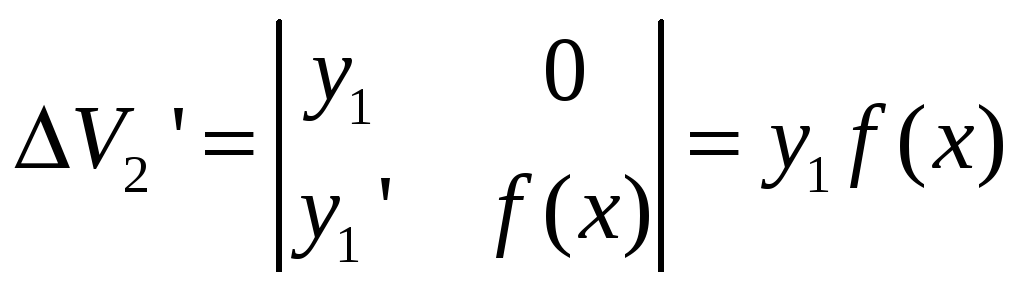
![]()
![]()
27. Линейные ду высших порядков
ДУ n-ого порядка называется
уравнение вида
![]()
Для определен.решенения необходимо задать n постоянных
С пост.коэф.:
![]()
1)![]()
![]() однородное
уравнения
однородное
уравнения
![]()
![]() - характеристическое уравнение.
- характеристическое уравнение.
![]() - корни характеристического уравнения.
- корни характеристического уравнения.
Если все корни – различные действительные
числа
![]()
Каждой паре комплексных сопр.корней
будет соответствовать
![]()
2)![]()
![]()
![]()
![]() S- кратность корня
S- кратность корня
28.Вронскиан, его свойства.
Средством изучения линейной зависимости систем функций является так называемый определитель Вронского.
Для 2-х дифференцируемых функций
![]() и
и
![]() вронскиан
имеет вид
вронскиан
имеет вид
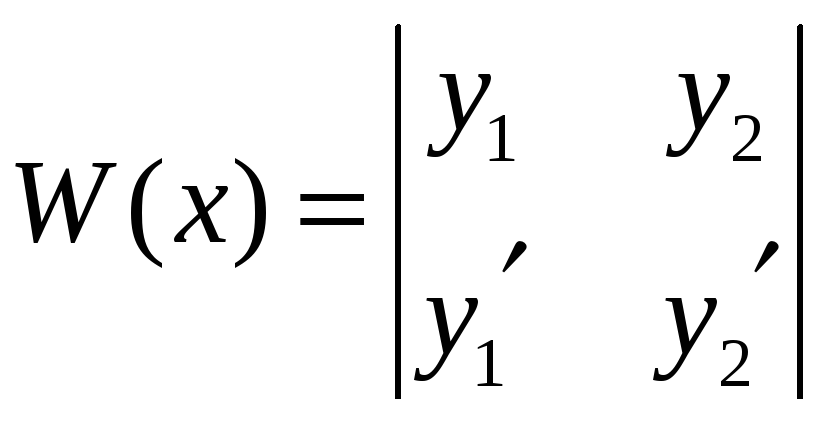
Если дифференцируемые функции
![]() и
и
![]() линейно зависимы на (a;b),
то определитель Вронского на этом
интервале тождественно =0.
линейно зависимы на (a;b),
то определитель Вронского на этом
интервале тождественно =0.
Если функции
![]() и
и
![]() линейно независимые решения на интервале
(a;b), то
определитель Вронского на этом интервале
нигде не обращается в ноль.
линейно независимые решения на интервале
(a;b), то
определитель Вронского на этом интервале
нигде не обращается в ноль.
29.Преобразования Лапласа.
Пусть f(x) – функция действительной переменной t, назовем ее оригиналом, если она обладает следующими свойствами:
1. f(t)![]() 0,
при t<0
0,
при t<0
2. f(t) непрерывна или имеет конечное число точек разрыва I рода и точки устранимого разрыва на любом конечном интервале.
3. существует такое M>0 и
S0![]() 0,
что для всех t
0,
что для всех t![]() 0
0
![]() ,
S0- показатель роста
f(t).
,
S0- показатель роста
f(t).
Прим: функция Хевисайта (единичная функция)
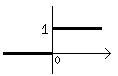
![]()
Пусть f(t) –
произвольная функция, являющаяся
оригиналом, и p=a+bi
– комплексное число такое, что Re
p![]() S0.
S0.
Преобразованием Лапласа называется выражение
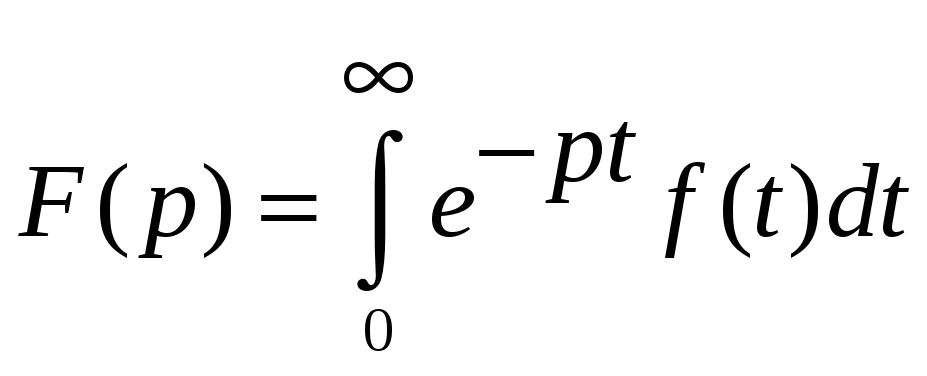 F(p)
– изображение f(t)
F(p)
– изображение f(t)
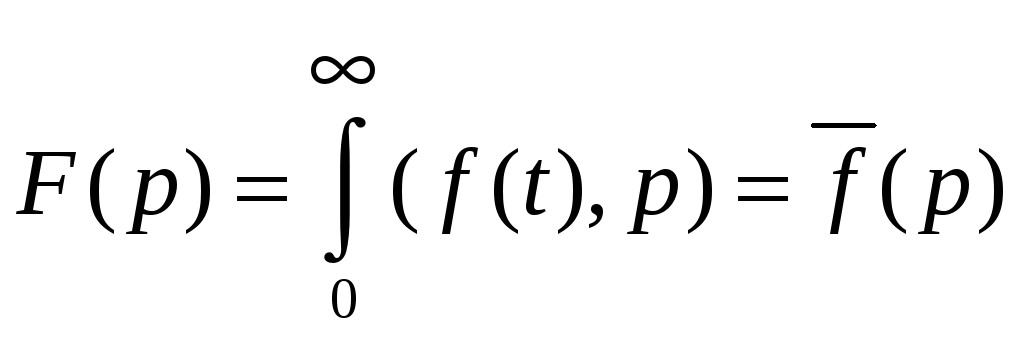
![]()
Всякому оригиналу соответствует изображение
Любой линейной комбинации оригиналов соответствует линейная комбинация их изображений
![]() k=1,2,…n
k=1,2,…n
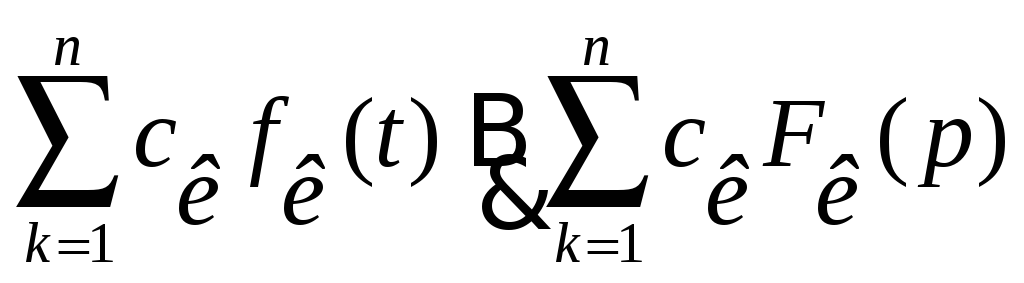
30.Свойства преобразований Лапласа
1.Линейность. Линейной комбинации
оригиналов соответствует такая же
линейная комбинация изображения.![]() ,
,
![]() ,
C1 и C2
– const.
,
C1 и C2
– const.![]()
2.Подобие. Если![]() ,
,![]() то
то
 ,
то есть умножаем аргумент оригинала на
положительное число
,
то есть умножаем аргумент оригинала на
положительное число
![]() приводит
к делению изображения и его аргумента
на это число.
приводит
к делению изображения и его аргумента
на это число.
3.Смещение (затухание). Если
![]() ,
a-const, то
,
a-const, то
![]() ,
т.е. умножение оригинала на функцию
,
т.е. умножение оригинала на функцию
![]() влечет за собой смещение переменной p.
влечет за собой смещение переменной p.
4. Запаздывание. Если
![]() ,
,
![]() ,
то
,
то
![]() ,
то есть запаздывание оригинала на
положительную величину
,
то есть запаздывание оригинала на
положительную величину
![]() приводит к умножению оригина без
запаздывания на
приводит к умножению оригина без
запаздывания на
![]() .
.
5. Дифференцирование оригинала.

6. Дифференцирование изображения.
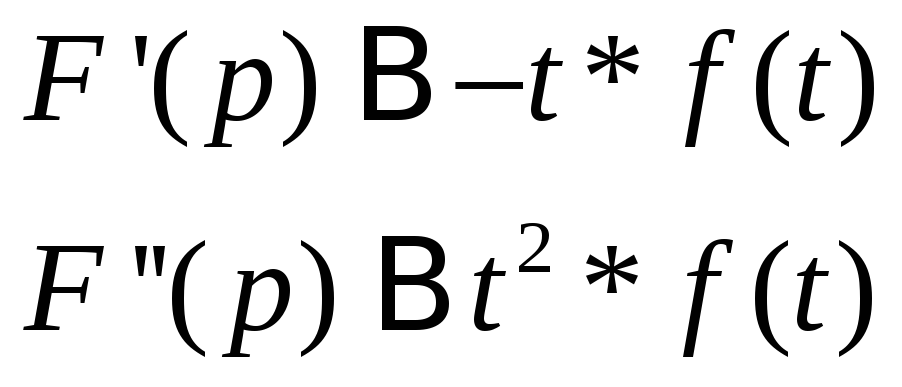
7.Интегрирование оригинала.
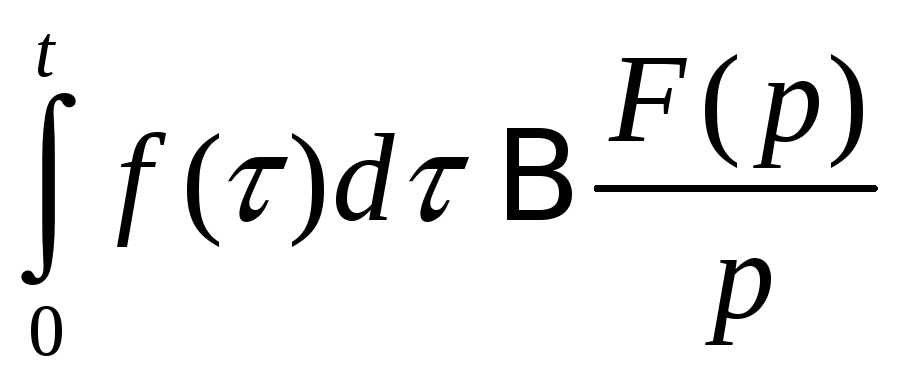
8.Интегрирование изображения.
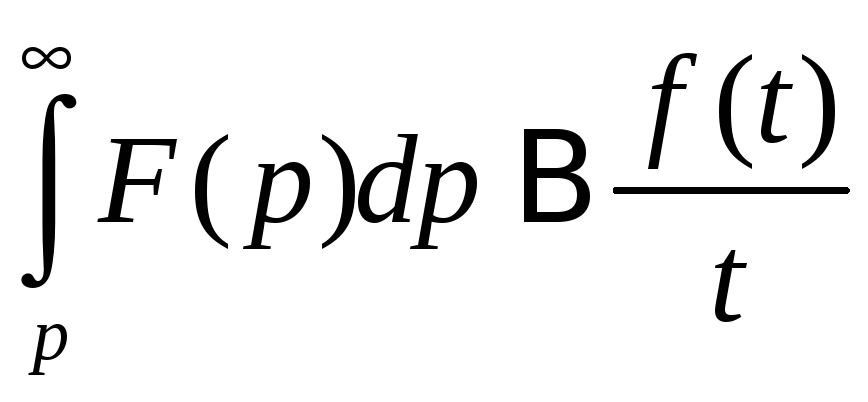
9.Умножение изображений.

10.Умножение оригиналов.
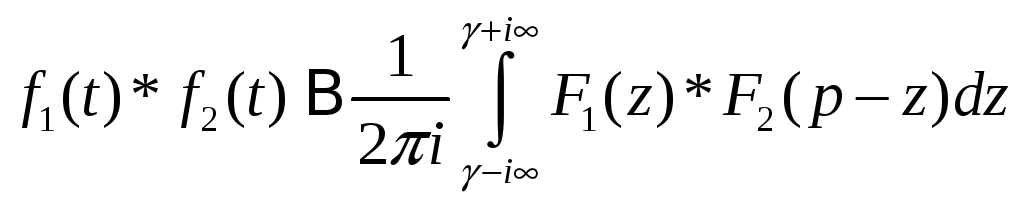
31.преобразование Лапласа элементарных функций.
1. f (t) Найти изображение процесса начавшегося t=t0 и закончившегося t=t1.
2.Найти изображение функции f(t), имеющей разное аналитическое задание на различных участках вещественной оси.
Удобно представить единичный импульс [t0;t1] следующим образом:

,
![]()
П
 ример:
ример:
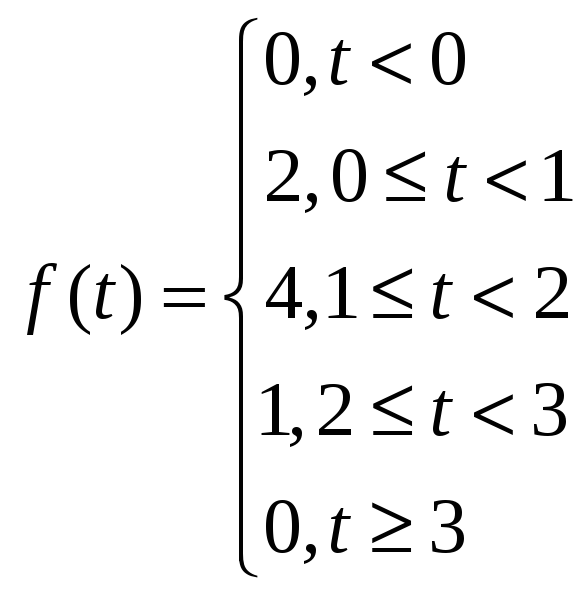





![]()
![]()
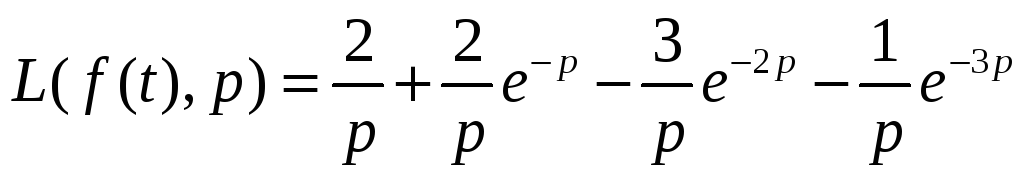
32. Свертка. Свойства свертки.
![]() ,
,![]() - оригиналы.
- оригиналы.
Сверткой
![]() и
и
![]() называется
интеграл
называется
интеграл
![]() *
*![]() =
=![]()
Свойства свертки:
1.
![]() - оригинал
- оригинал
2.
![]() =
=![]()
3. (![]() )
)![]()
![]() =
=![]() (
(![]()
![]() )
)
4.
![]() (
(![]() +
+![]() )=
)=![]() +
+![]()
![]()
33.Применение преобразования Лапласа при решении дифференциальных уравнений.
ДУ II порядка с постоянными коэффициентами.
![]()
![]()
![]()
![]() -
оригиналы.
-
оригиналы.
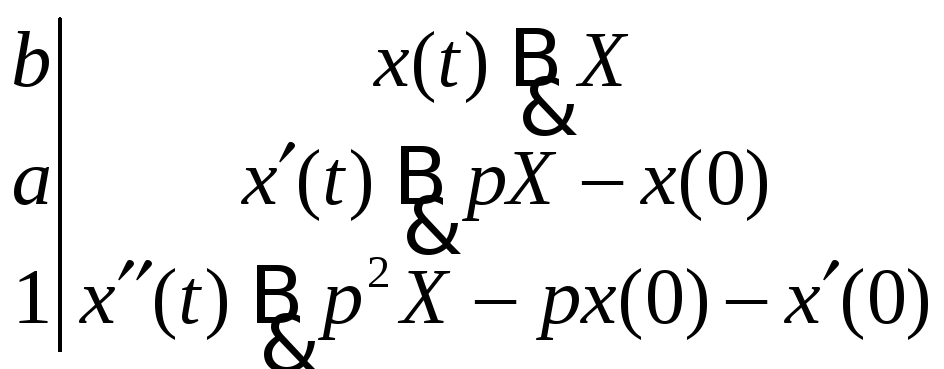
![]()
![]()
![]()
![]()
ДУ с постоянными коэффициентами n-ого порядка.
![]() ,
где
,
где
![]() - числа;
- числа;
![]() - оригиналы.
- оригиналы.
![]()
![]() …
… ![]()
![]()
![]()
![]()
если
![]()
34.Линейные однородные системы дифференциальных уравнений.
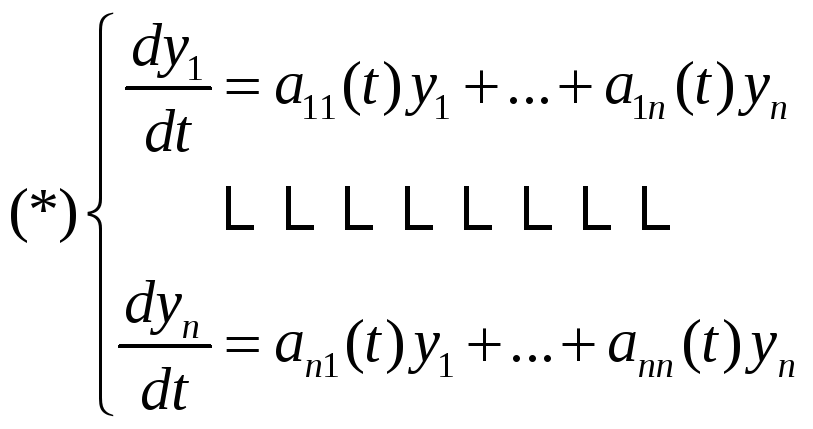
![]() -
функция, непрерывная на интервале (a;b),
называется коэффициентом, система
называется линейной однородной системой
ДУ I порядка.
-
функция, непрерывная на интервале (a;b),
называется коэффициентом, система
называется линейной однородной системой
ДУ I порядка.
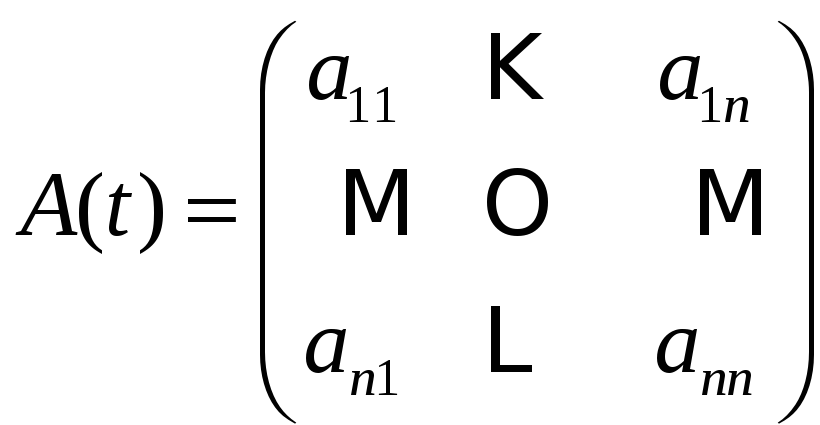
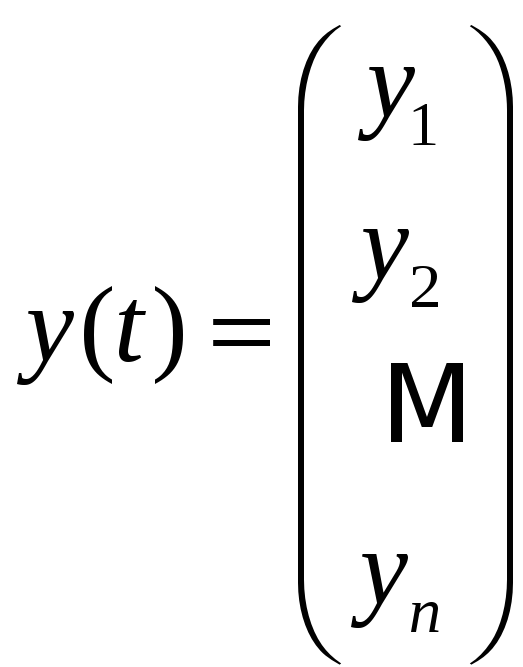 -
вектор
-
вектор
![]() - краткая запись системы (*)
- краткая запись системы (*)
Решением данной системы называется
совокупность функций
![]() - непрерывных на интервале (a;b),
удовлетворяющих условию (*) и образующих
каждое уравнение системы (*) в тождество.
- непрерывных на интервале (a;b),
удовлетворяющих условию (*) и образующих
каждое уравнение системы (*) в тождество.
Задача Коши для системы (*) – это задача
для нахождения решений этой системы,
удовлетворяющих начальным условиям.
Пусть система (*) имеет решения
![]() ;
;
![]() - общее решение. Система решений называется
линейно независимой на интервале (a;b),
если из равенства
- общее решение. Система решений называется
линейно независимой на интервале (a;b),
если из равенства
![]()
![]() =0
=0
Чтобы найти общее решение системы (*),
надо найти и линейно независимое решение
системы, тогда
![]()
Общее решение линейной неоднородной системы ДУ с постоянными коэффициентами
![]()
![]() ,
где
,
где
![]() - числа
- числа

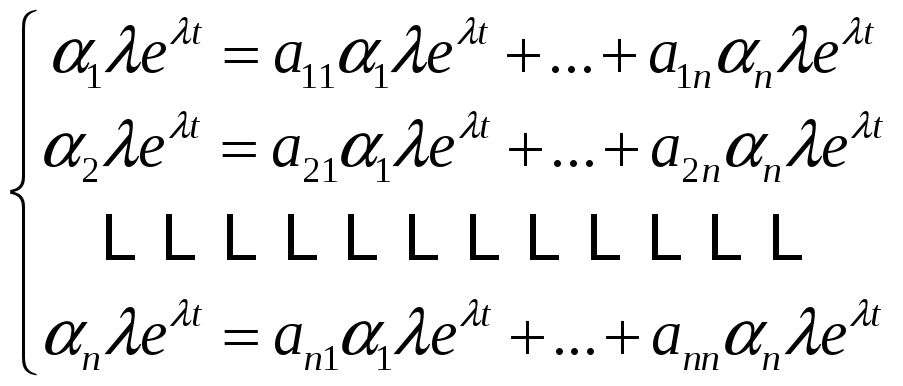
Однородная система ДУ имеет решение,
если
![]() =0
(
=0
(![]() )
)
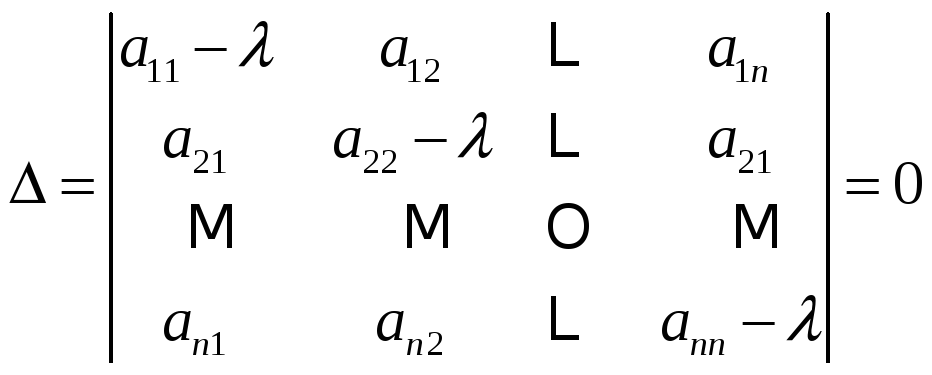
характеристическое уравнение
![]() - собственные числа. Многочлен имеет n
корней
- собственные числа. Многочлен имеет n
корней
1. если все корни характеристического
уравнения различны, то:

2. если
![]() имеет кратность m, то
имеет кратность m, то
![]() ,
где
,
где
![]() -
полином степени (m-1)
-
полином степени (m-1)
Пример:
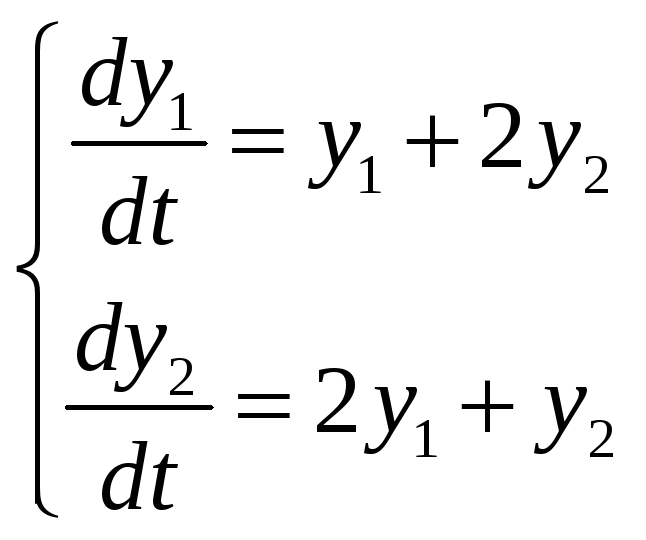
![]() =0
=0 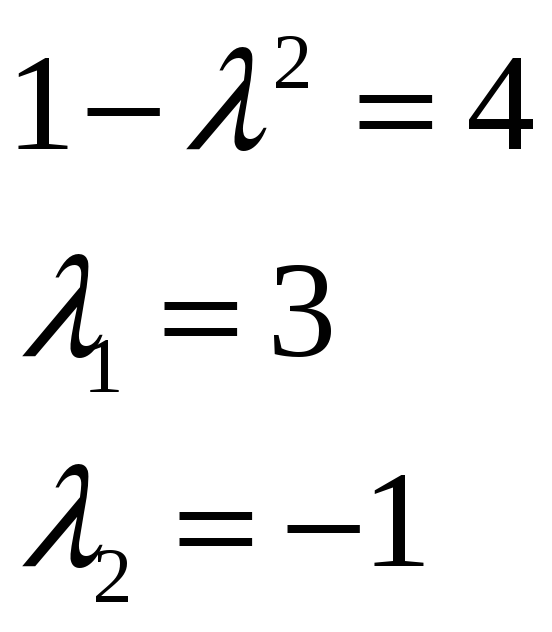
 ответ:
ответ: