
- •8. Преобразование матрицы линейного оператора при переходе к новому базису.
- •9.Собственные значения и собственные вектора линейных операторов:
- •10. Свойства собственных значений и собственных векторов линейного оператора.
- •11.Квадратичные формы. Определение. Примеры.
- •12. Преобразование квадратичной формы к каноническому виду.
- •13. Приведение к каноническому виду уравнений кривых и поверхностей 2-го порядка:
- •14.Каноническое уравнение кривых и поверхностей II порядка (см.Реферат)
- •15.Дифференцильные уравнения (основные понятия, примеры)
- •16.Ду I порядка. Задача Коши.
- •17.Уравнение, с разделяющимися переменными.
- •18. Однородные уравнения I порядка.
- •19.Линейные уравнения первого порядка.
- •24.Однородные дифференциальные уравнения с постоянными коэффициентами.
- •25. Линейные неоднородные уравнения с постоянными коэффициентами:
- •26. Метод вариаций произвольных постоянных.
- •27. Линейные ду высших порядков
- •28.Вронскиан, его свойства.
- •29.Преобразования Лапласа.
- •30.Свойства преобразований Лапласа
- •35.Решение систем дифференциальных уравнений операционным методом.
13. Приведение к каноническому виду уравнений кривых и поверхностей 2-го порядка:
(См. 12)
Пример:
![]()
![]()
![]()
![]()
![]()
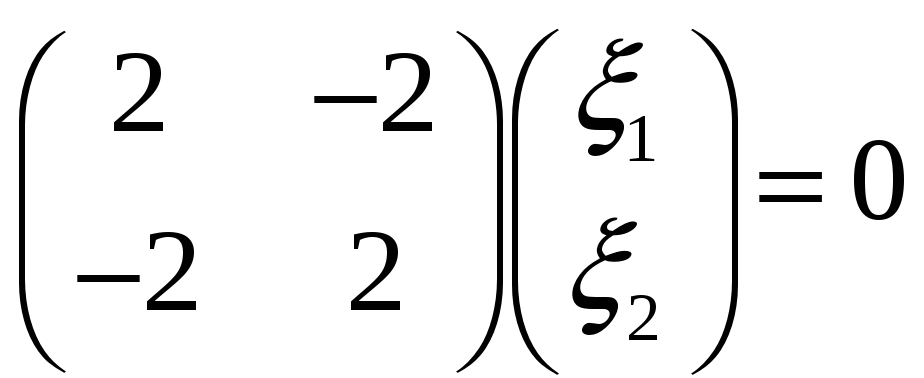
![]()
![]()
![]()
![]()
![]()
![]()
 =1>0,
след. прав ориентации
=1>0,
след. прав ориентации

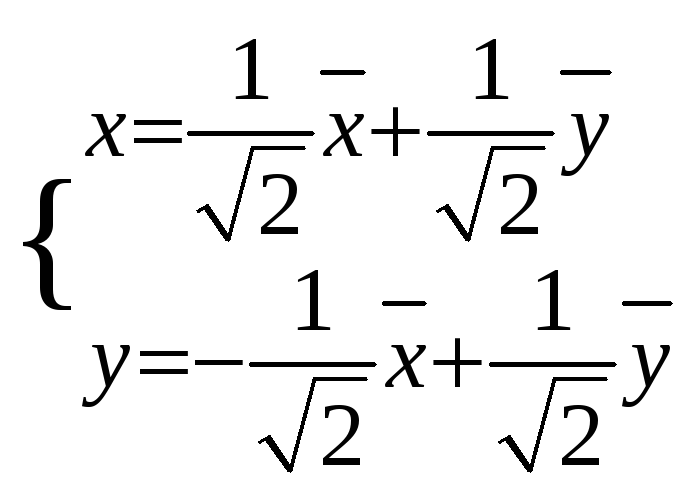
![]()
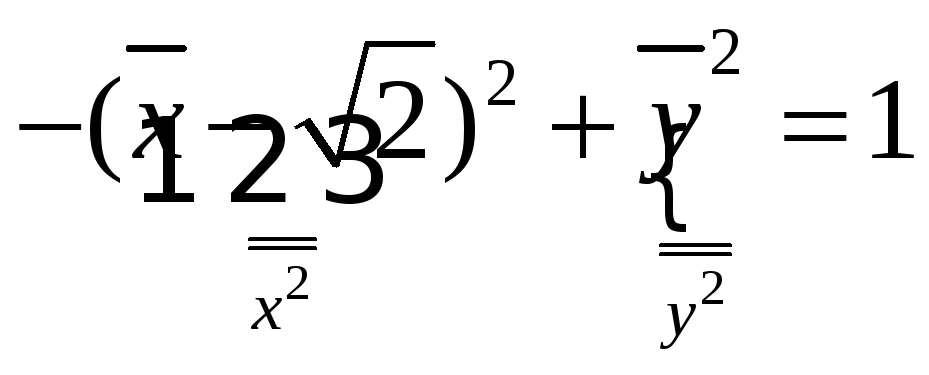
![]()
14.Каноническое уравнение кривых и поверхностей II порядка (см.Реферат)
Ax2+Bxy+Cy2+Dx+Ey+F=0 – алгебраическое уравнение кривой 2 порядка относительно переменных x и y.
Эллипс
![]() ;
если a=b,
;
если a=b,
![]()
![]() окружность.
окружность.
Гипербола
![]()
Парабола
![]()
![]() - уравнение поверхности второго порядка
относительно трех переменных.
- уравнение поверхности второго порядка
относительно трех переменных.
Если D=E=F![]() каноническое уравнение.
каноническое уравнение.
Конус
![]()
Цилиндр эллиптический
![]()
Гиперболический цилиндр
![]()
Параболический цилиндр
![]()
Однополостной гиперболоид
![]()
Двуполостной гиперболоид
![]()
Гиперболический параболоид
![]()
Эллипсоид
![]()
Эллиптический параболоид
![]()
15.Дифференцильные уравнения (основные понятия, примеры)
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию у(х) и производные этой функции по х различных порядков.
Порядок старшей производной называется порядком уравнения.
Дифференциальное уравнение называется
линейным, если левая часть этого уравнения
– многочлен первой степени относительно
неизвестной функции у и ее производных
![]()
![]()
Функции
![]() ,
определенные и непрерывные в определенном
интервале, называются коэффициентами
уравнения; f(x)
– свободный член.
,
определенные и непрерывные в определенном
интервале, называются коэффициентами
уравнения; f(x)
– свободный член.
Пример:
![]() - линейное.
- линейное.
Линейное уравнение называют однородным, если f(x) тождественно равно нулю, в противоположном случае – неоднородным.
Всякая функция
![]() ,
которая при подстановке в ДУ превращает
его в тождество, называется решением
этого уравнения.
,
которая при подстановке в ДУ превращает
его в тождество, называется решением
этого уравнения.
Общим решением ДУ
![]() называется такое решение
называется такое решение
![]() ,
которое содержит столько постоянных
,
которое содержит столько постоянных
![]() ,
каков порядок уравнения.
,
каков порядок уравнения.
16.Ду I порядка. Задача Коши.
![]()
![]()
![]() - общее решение ДУ I порядка.
- общее решение ДУ I порядка.
Геометрически общее решение ДУ I порядка – семейство интегральных кривых, соответствующих различным значениям постоянных.
Найти решение
![]() ,
удовлетворяющее условию
,
удовлетворяющее условию
![]()
Геометрически надо найти интегральную
кривую ДУ
![]() ,
проходящую через точку
,
проходящую через точку
![]()
Уравнение
![]() имеет бесконечное число решений, но
если выбр.начальн.услов., то решение
существует и только единственное.
имеет бесконечное число решений, но
если выбр.начальн.услов., то решение
существует и только единственное.
17.Уравнение, с разделяющимися переменными.
ДУ I порядка называется
уравнением с разделяющимися переменными,
если оно имеет вид
![]()
![]()
![]()
Пример:![]()
![]()
![]()
![]() ,
где
,
где
![]()
![]()
18. Однородные уравнения I порядка.
Функция
![]() называется
однородной в степени n,
если
называется
однородной в степени n,
если
![]()
![]()
если
![]() и
и
![]() - однородные функции одного и того же
порядка
- однородные функции одного и того же
порядка
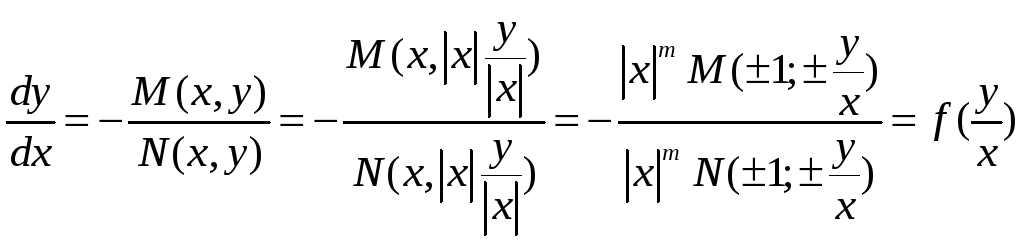
![]() Обозначим
Обозначим
![]() y=xz
y=xz
![]()
![]() уравнение
с разделяющимися переменными.
уравнение
с разделяющимися переменными.
![]()
![]()
![]()
19.Линейные уравнения первого порядка.
Уравнение вида
![]() ,
где
,
где
![]() и
функции f(x)
и p(х) – непрерывные функции
на (a,b),
называется дифференциальным линейным
уравнением первого порядка.
и
функции f(x)
и p(х) – непрерывные функции
на (a,b),
называется дифференциальным линейным
уравнением первого порядка.
Если f(x) тождественно =0, следовательно, уравнение называется однородным.
Методы решения линейного уравнения:
1)метод Бернулли:
ищем решение в виде произведения функции y=u(x)v(x)
![]()
![]()
![]()
Подберем v(x) ![]()
![]()
![]()
![]()
![]()
![]() - общее решение
- общее решение
Общее решение линейного неоднородного уравнения = решению соответствующего однородного уравнения и частного решения неоднородного уравнения.
2) Метод Лагранжа:
![]()
![]() -
общее решение однородного уравнения
-
общее решение однородного уравнения
Пусть с=с(х) – функция
![]() - неоднородное уравнение
- неоднородное уравнение
20.Уравнение Бернулли:
![]() ,
где
,
где
![]() -
любое число
-
любое число
Если
![]() =1,
=1,
![]() =0-
линейное уравнение
=0-
линейное уравнение
Если
![]()
![]() 0,
0,
![]()
![]() 1,
то:
1,
то:
![]() ,
,
![]()
![]()
![]() -
линейное уравнение от z(x)
-
линейное уравнение от z(x)
21.Уравнение Рикатти:
![]() ,
где p, q, z-
функции от х.
,
где p, q, z-
функции от х.
Пусть
![]() -
частное решение, т.е.
-
частное решение, т.е.
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]() (линейное
уравнение от u(x)
(линейное
уравнение от u(x)
22.Дифференциальные уравнения второго порядка:
![]()
![]()
![]() -
общее решение
-
общее решение
![]() -
частное решение.
-
частное решение.
![]() ,
,
![]()
Если в уравнении
![]() функции и ее частные производные
непрерывны в некой области D,
то любой точки этой области существует
единственное решение
функции и ее частные производные
непрерывны в некой области D,
то любой точки этой области существует
единственное решение
![]() ,
удовлетворяющее начальному условию.
,
удовлетворяющее начальному условию.
1)![]() .
Пусть
.
Пусть
![]() ,
,
![]()
![]() ,
,
![]() +с,
+с,
![]()
![]()
2)
![]() Пусть
Пусть
![]() ,
,
![]()
![]() ,
,
![]()
3)
![]() Пусть
Пусть
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
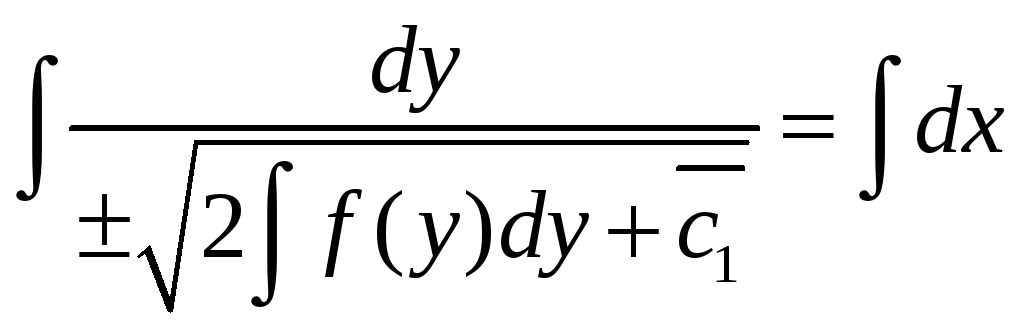 ,
,
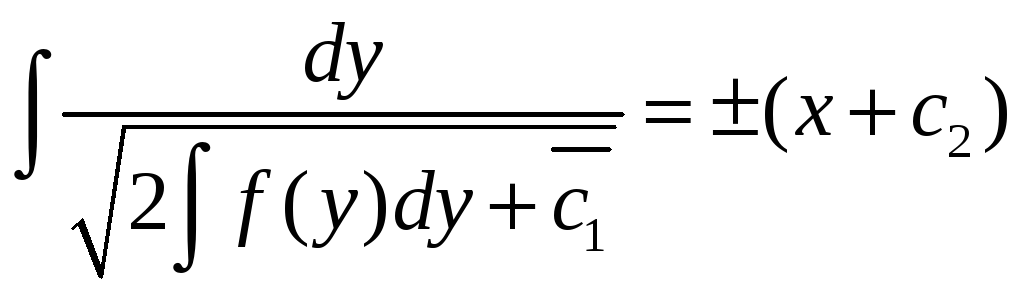
23.Общие свойства решений линейных однородных дифференциальных уравнений II порядка.
![]() (1) где
(1) где
![]() и
и
![]() - непрерывные функции.
- непрерывные функции.
![]() и
и
![]() - частные решения.
- частные решения.
2 решения
![]() и
и
![]() называются линейно независимыми, если
только тривиальные линейные комбинации
этих функций =0 и линейно зависимыми,
когда хотя бы 1 из них можно выразить
через другой.
называются линейно независимыми, если
только тривиальные линейные комбинации
этих функций =0 и линейно зависимыми,
когда хотя бы 1 из них можно выразить
через другой.
(![]() - линейная комбинация)
- линейная комбинация)
![]() и
и
![]() - независимы
- независимы
![]()
![]()
если
![]()
Пример:
![]()
![]()
 (
(![]() - независ.)
- независ.)
Функции
![]() и
и
![]() дифференцируемы и непрерывны на
(a;b)линейно
зависимы, если определитель Вронского
на этом интервале тождественно = 0, и
линейно независимы, если вронскиан
дифференцируемы и непрерывны на
(a;b)линейно
зависимы, если определитель Вронского
на этом интервале тождественно = 0, и
линейно независимы, если вронскиан
![]() 0.
0.
Определитель Вронского от непрерывных
и дифференцируемых функций
![]() - определитель n-ого
порядка, в первой строке которого
находятся функции, во второй – первые
производные и т..
- определитель n-ого
порядка, в первой строке которого
находятся функции, во второй – первые
производные и т..
Если функции
![]() и
и
![]() являются линейно независимым решением
уравнения (1), то общее решение этого
уравнения есть линейная комбинация
этих решений. (
являются линейно независимым решением
уравнения (1), то общее решение этого
уравнения есть линейная комбинация
этих решений. (![]() )
)
Доказательство:
![]()
![]()
![]()
![]()
![]() ,
ч.т.д.
,
ч.т.д.
Чтобы найти общее решение ДУ вида (1)
достаточно знать 2 частных линейно
независимых решения этого уравнения
![]() и
и
![]() ,
тогда
,
тогда
![]()
