1.Линейные пространства (определение, примеры): Множество L называется линейным пространством, а его элементы векторами, если:

- задан закон, по которому любым двум элементам из множества L сопоставляется элемент z, принадлежащий L, и называется суммой x и y.

- задан закон умножения оператора на число, по которому элементу x из множества L и числу α, соотв. элем. y L, такой, что y= αx.

- для любых x,y и zL и любых чисел α,β выполняются следующие аксиомы и :

1. x+y=y+x 2. (x+y)+z=x+(y+z) 3. такой эл-т О (нулев. эл-т)

4. , , ((-х) – противоположный элемент)

5. α(x+y)= αx+ αy 6.( α+β)x= αx+βx 7. α(βx)=(αβ)x 8. x*1=x

Прим: 1) v- множество векторов на плоскости; v – линейное пространство

2)p – множество многочленов от 1ой переменной степени не выше 5; p - линейное пространство.

2.Линейная зависимость (независимость) векторов: - вектора, принадлежащие L, - вещественные числа.

Выражение вида называется линейной комбинацией векторов с коэффициентами .

Система векторов называется линейно зависимой, если существует равная О нетривиальная (невырожден. – хотя бы 1 из коэффициентов отличен от нуля) линейная комбинация этих векторов. В противоположном случае система называется линейно независимой.

Система векторов линейно зависима тогда, когда, по крайней мере, один из этих векторов является линейной комбинацией остальных.

Доказательство: 1. необходимо

Пусть - линейно зависимая система векторов

Пусть

Следовательно, линейная комбинация векторов.

2. Достаточно.

Пусть (линейная комбинация векторов)

(-1)*

т.к., следовательно, система векторов линейно зависима.

Если в систему векторов входит нулевой вектор, то эта система будет линейно зависима.

Если какая-либо часть системы линейных векторов линейно зависима, то и вся эта система линейно зависима.

3. Базис. Координаты вектора. Размерность пространства. Система линейно независимых векторов называется базисом пространства L, если любой вектор x из этого пространства может быть представлен в виде линейной комбинации этих векторов. А числа называются координатами вектора относительно данного базиса. Если задан базис, то координаты вектора в данном базисе определены однозначно.

Доказательство:

Пусть - базис. Предположим, что x разложен двумя способами.

==0

Т.к. линейная комбинация = 0, а вектора линейно независимы =0, следовательно .

Пусть в линейном пространстве L выбран базис , тогда:

1. при сложении векторов их координаты складываются.

2. При умножении вектора на число его координаты умножаются на это число.

Доказательство: 1. xL, yL, , ,

2. α – число

Если в линейном пространстве L существует базис из n векторов, то любой другой базис этого пространства так же содержит n векторов.

Линейное пространство L, в котором базис состоит из n векторов называется n-мерным, а число n - размерностью пространства Lⁿ

4.Подпространство. Линейное нормированное пространство. Евклидово пространство. Непустое множество Z векторов в линейном пространстве L называется линейным подпространством, если для любых х и y принадлежащих Z: (x+y)=Z и для любого вектора xZ α- число (αx) Z.

Множество называется линейным нормированным пространством, если для любого вектора х, принадлежащего этому множеству поставлено в соответствие вещественное число x - вещественное число, называемое нормой элемента х, причем выполняются следующие условия:

1. Если норма 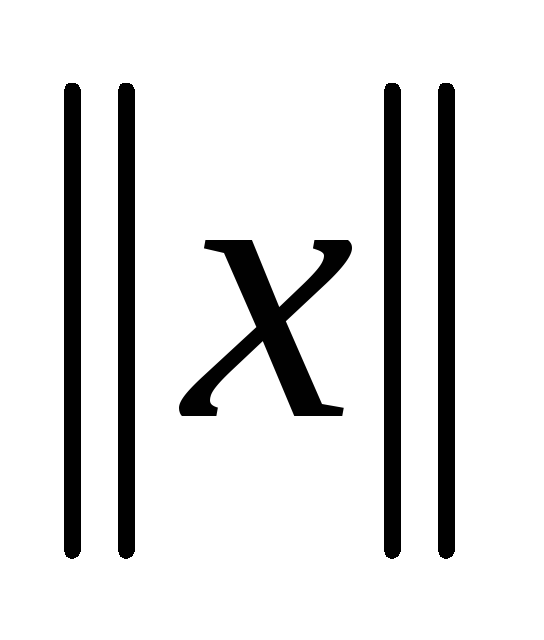=0, то х=0.

2. Для любого числа αR или αС, 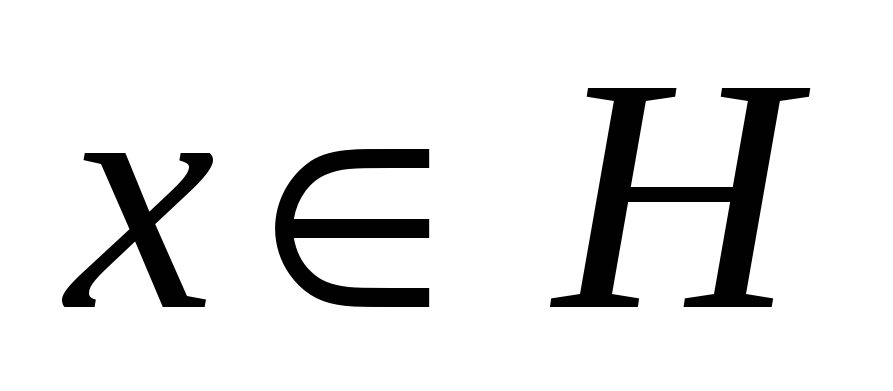норма от произведения αх будет

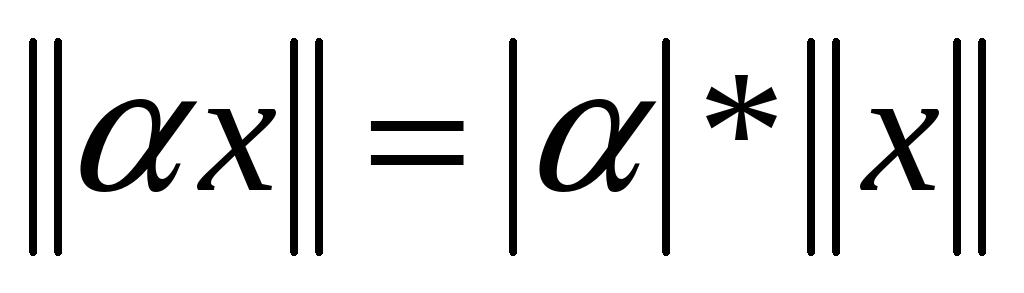
3. Для любого элемента х, y, принадлежащего Н .

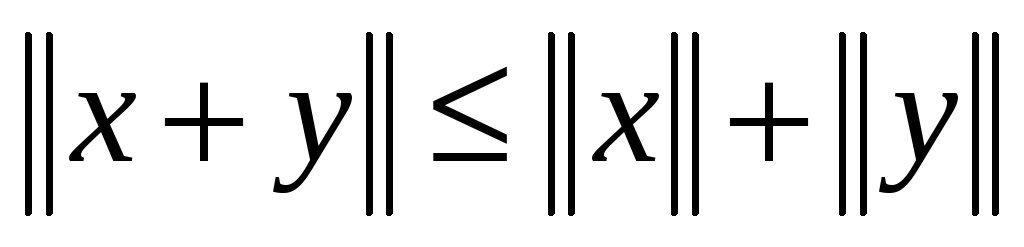Линейное пространство называется евклидовым, если в этом пространстве определено скалярное произведение векторов. Каждому x и y поставлено в соответствие действительное число (x,y), причем выполняется следующее:

1. (x,y)=(y,x) 2. (λx,y)= λ(x,y)=(x, λy) 3. (x₁+x₂,y)=(x₁,y)+(x₂,y)

4. (x,y)0 5. ()

Норма вектора x, равен в евклидовом пространстве называется длиной вектора и обозначается =

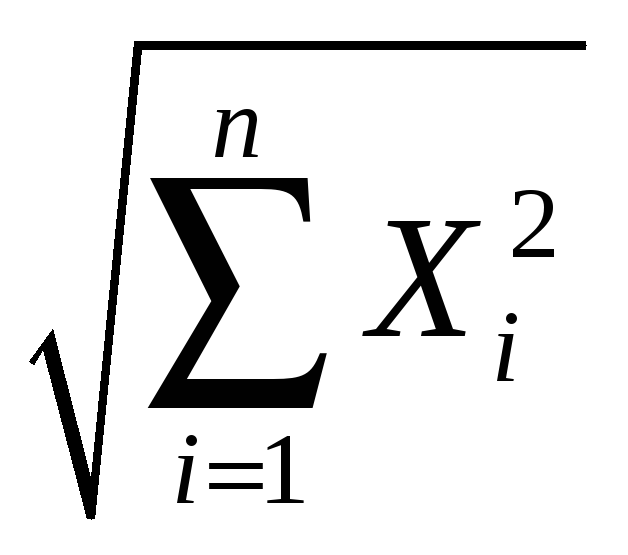
Вывод:

1. Если x и y принадлежат евклидовому пространству размерности n, тогда (x,y)=

2. x,y 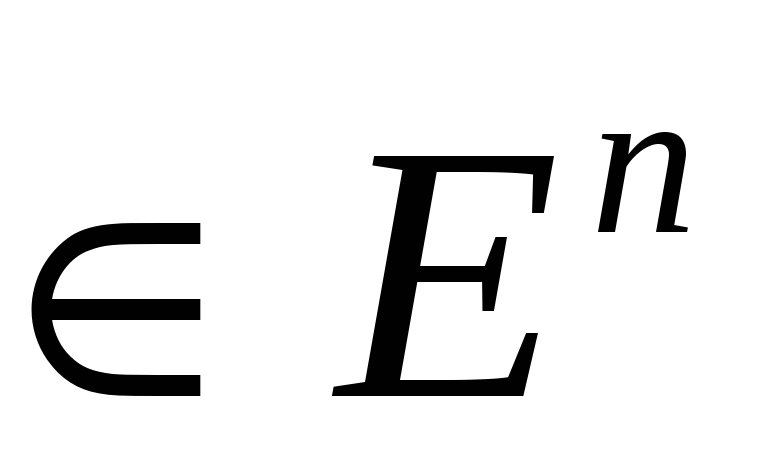и ортогональны, если их скалярное произведение = 0 ((x,y)=0) и ,

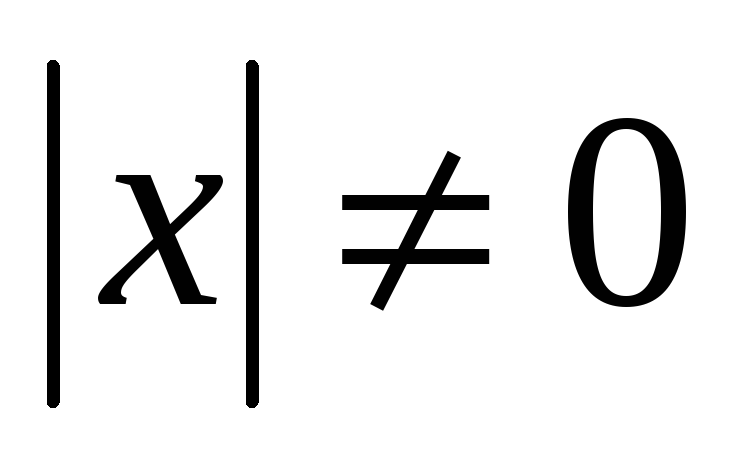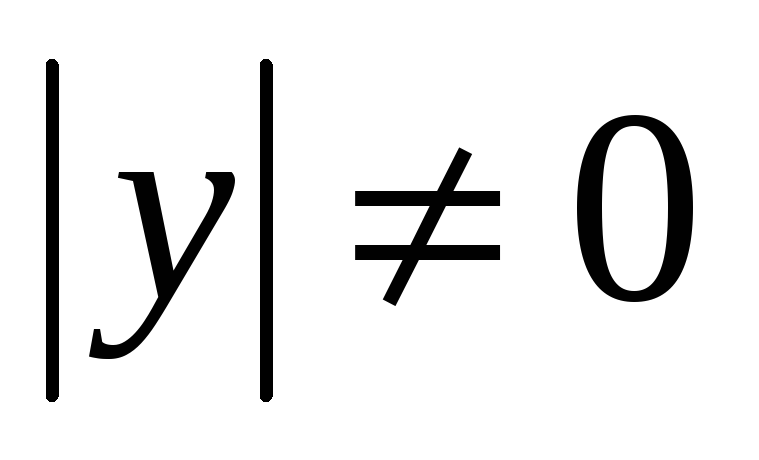
Система ненулевых векторов образует ортогональный базис в , если эти вектора попарно ортогональны, и ортонормальный базис, если каждый из векторов имеет длину =1.

5.Линейные операторы (определение, примеры). Пусть H и F – линейные пространства. Оператором A, действ. из H в F называется отображение вида A : Н F. Сопост. любому элементу

y=A(x)=Ax

Оператор А называется линейным, если для любых х₁,х₂ H , число.

1.

2.

Примечание:

1.А-умножается на число

,-число, x-вектор,

A-линейный оператор

2. M ⁿ –линейное пространство,A-оператор дифференц.

-линейный оператор

6.Матрица линейного оператора. Образуется следующим образом:

матрица: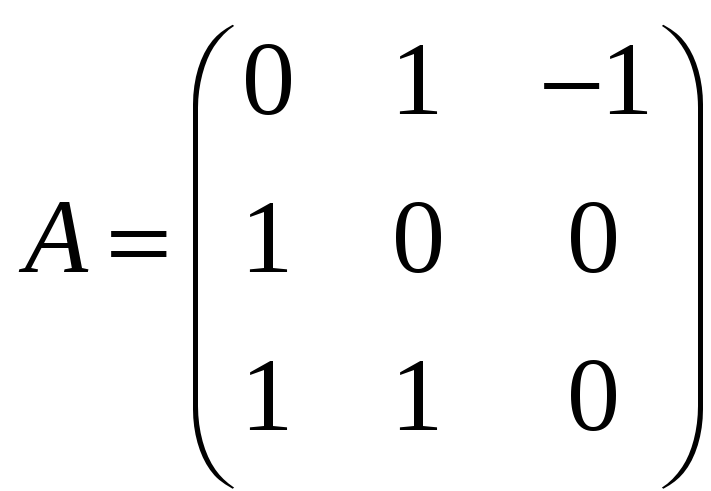

Пусть в заданном базисе лин. простр. каждому линейному опреатору А отвечает матрица , , тогда при сложении линейных операторов соответствующие им матрицы складываются, при умножении матрицы на число соответствующая матрица умножается на число, при умножении операторов соответствующие матрицы перемножаются.

7.Действия с линейными операторами. Два линейных оператора A и B называются равными и принадлежат тому же пространству, если результат их действий на один и тот же элемент х, принадлежащий к дает один и тот же элемент y.

Ax=y, Bx=y, следовательно, А=В.

Под суммой двух операторов А и В понимают третий оператор С, полученный в результате действий каждого из операторов на элементе х, принадлежащему к и суммирование результатов действий.

А+В=В+А; А+В+D=(A+B)+D=A+(B+D)

Произведением двух операторов называется оператор который получен в результате последовательно выполнения данных операторов, причем сначала действует тот оператор, который стоит ближе к элементу. A*Bx=A(Bx)

Если для любого х, принадлежащего , Ex=x, то Е – единичный оператор.

Свойства произведения:

1. A*Ex=Ax=E*Ax 2.x=A(Ax) 3.A*B(C)x=A(BC)x=(AB)Cx

4. (A+B)Cx=ACx+BCx 5. Если A*A^-1x= A^-1*Ax=Ex=x, то A^-1-обратный оператор.

8. Преобразование матрицы линейного оператора при переходе к новому базису.

А – линейный оператор. Ах=у, (х,у)

- базис в ;

=

- новый базис.

Т – матрица перехода от старого базиса к новому.

АА’, xx’, yy’, Ax’y’

x=Tx’; y=Ty’.

Пусть Ax=Atx’; y=Atx’; Ty’=ATx’; y’=T^-1ATx’; A’x’= T^-1ATx’;

A’= T^-1AT – формула перехода.

При переходе линейного оператора из базиса в базис матрица линейного оператора меняется, а определитель остается прежним.

9.Собственные значения и собственные вектора линейных операторов:

Пусть , А- линейный оператор в , вектор , удовлетворяющий соотношению , называется собственным вектором, а собственное число -собственным значением линейного оператора А.

Пусть - прямая, тогда любой вектор на этой прямой является собственным.

В комплексном пространстве всякий линейный оператор А имеет хотя бы один собственный вектор.

Доказательство:

1.

2.

3. Пусть

4.

(*)

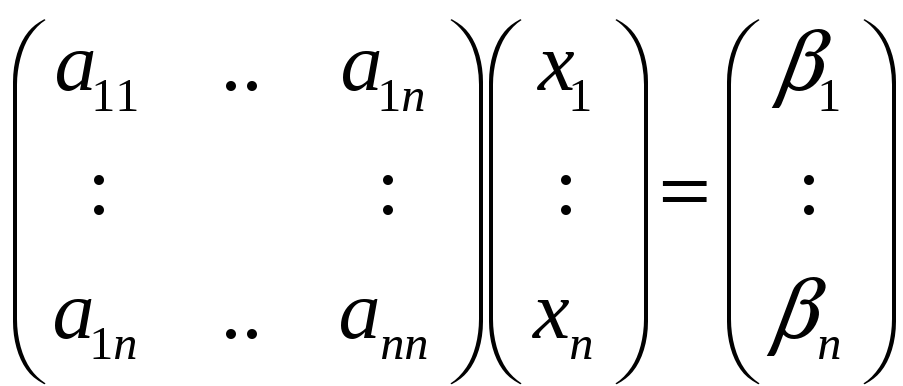
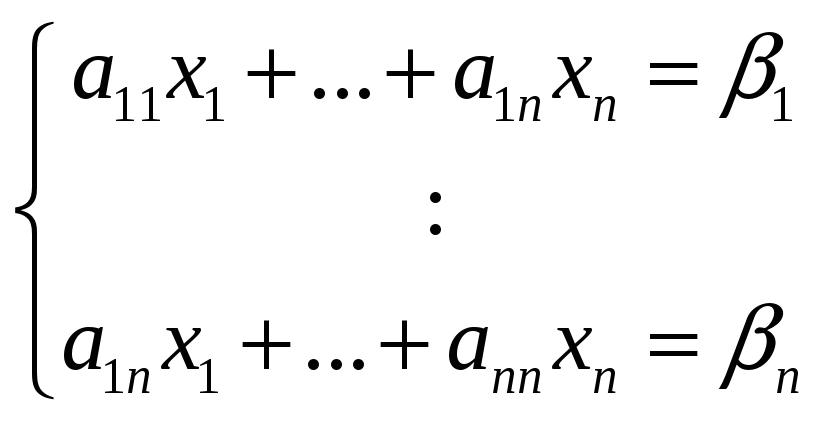
5.Пусть х- собственный

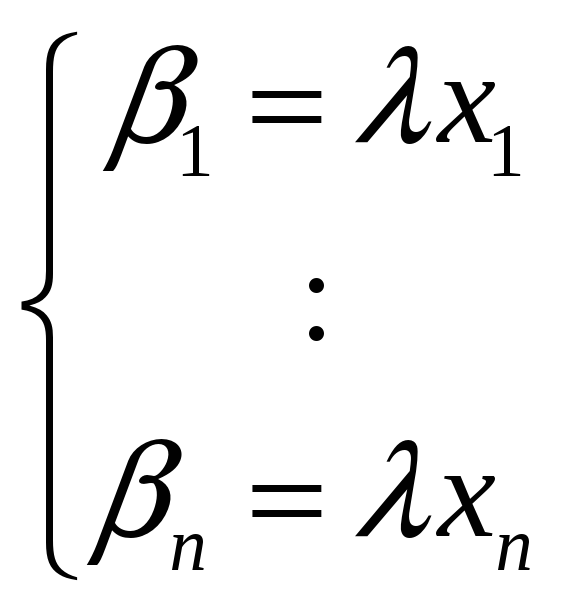, заменим в (*)

(**)

(**)- однородная система линейных уравнений, всегда имеет тривиальное решение, а чтобы имела нетривиальное, необходимо, чтобы определитель системы = 0.

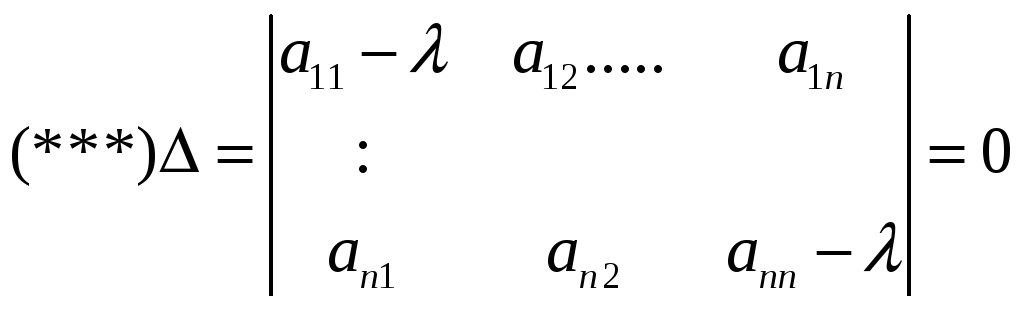
Пусть - корень уравнения n-ой степени относительно (***)

Подставим в систему (**)

- собственный вектор

Для каждого собственного числа имеется свой вектор.

10. Свойства собственных значений и собственных векторов линейного оператора.

- характеристический многочлен А, а следовательно, и собств.значен.А не зависят т выбора базиса, а определяются только самим оператором.

Собственный вектора оператора А, соответствуют различным собственным знчениям, линейно независ.

Если характеристический многочлен оператора А имеет n различных корней, то матрица А может быть приведена к диагональной форме.

Рассмотрим матрицу линейного оператора А в базисе из собственных векторов, т.к. все значения различны, то:

1. А – матрица линейного оператора в диагональном виде.

- сумма диагональных элементов

- сумма главных миноров II порядка

- определитель A

2. А – треугольная матрица, то собственными числами будут числа, стоящие на диагонали

11.Квадратичные формы. Определение. Примеры.

К.ф. – многочлен второй степени, относительно переменных не содержит свободного члена и члена в первой степени.

Числа называются коэффициентами квадратичной формы.

Если - к.ф., тогда если мы умножаем каждую переменную на действит. α

Примечание:

Квадратичная форма может быть записана в матричном виде:

=

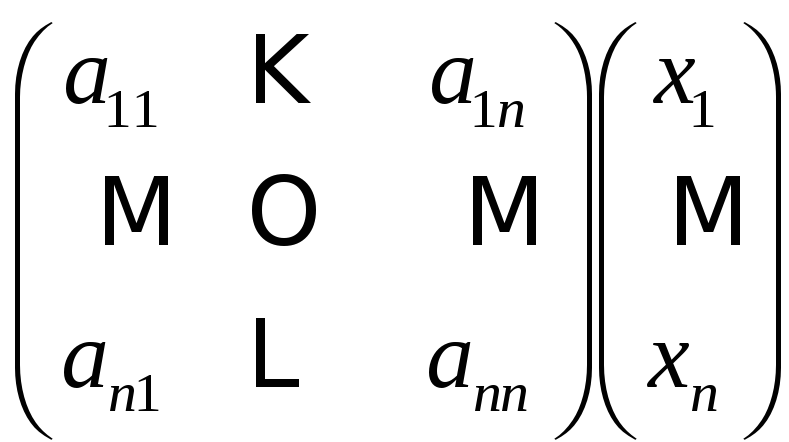
Обозначим за х матричный столбец, следовательно, =x^TAx (A- матрица квадратичной формы). Если при изменении базиса координаты вектора х меняются, то есть , то к.ф. может быть записана как к.ф. через , но с другими коэффициентами.

= x^TAx х=Lx’ (L-матрица перехода)

=(Lx’)^TA(Lx’)=(x’)^TL^TALx’=(x’)^TBx’

12. Преобразование квадратичной формы к каноническому виду.

Если матрица квадратичной формы диагональна, то к.ф. имеет канонический вид.

Пусть f(х) - к.ф. в пространстве , тогда можно найти ортонормированный базис, в котором эта к.ф. записывается диагональной матрицей.

Доказательство: пусть - ортонормированный базис из собственных векторов матрицы квадратичной формы А.

<Аx,x>=<A,>=<,>=<,>=+=

Приведение квадратичной формы второго порядка к каноническому виду:

= в

1) составим матрицу А: А=

2) находим корни характеристического уравнения:

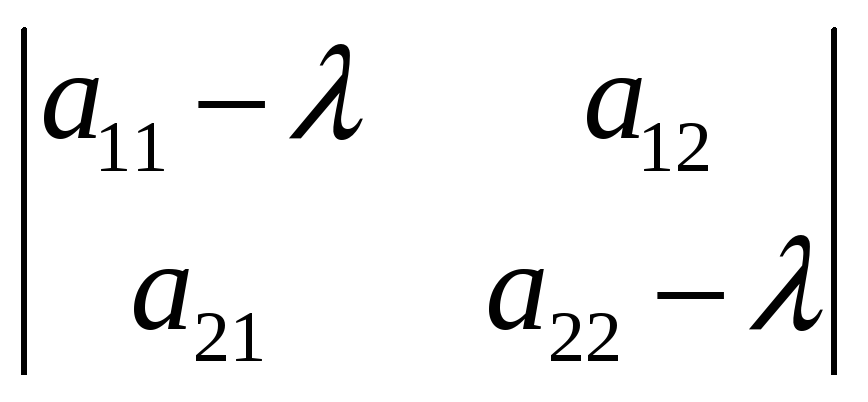=0 λ₁,λ₂ - корни 3) Находим собственные вектора, соответствующие числам λ₁ и λ₂.

,

Из них выбираем два вектора, ортогональные между собой и единичн. и - базисные вектора.

4) Составим матрицу перехода:

={e₁,m₁}, ={e₂,m₂} S(матрица перехода)=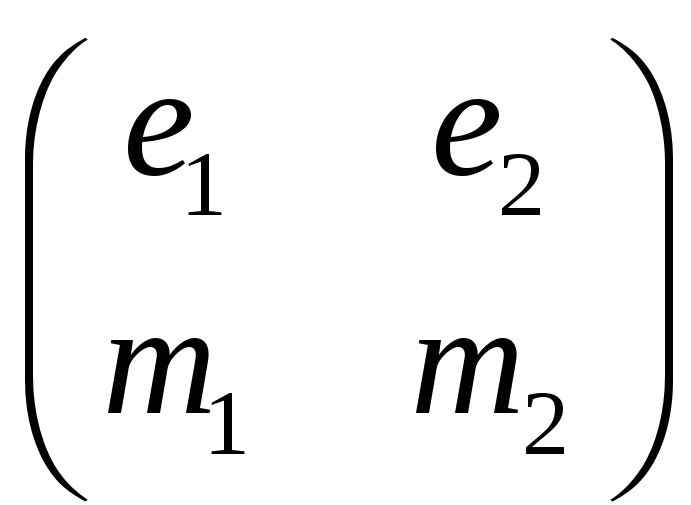

detS>0 (для сохранения взаимного ориент. новых векторов)

5) Переход к новому базису

= =

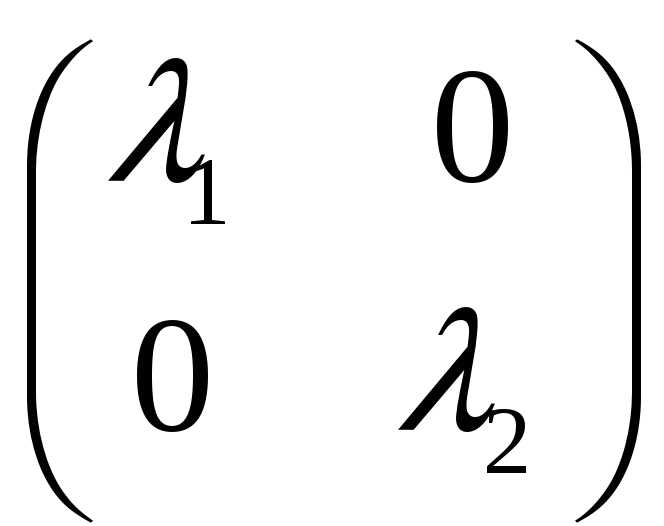
Направление собственных векторов при образовании x’=Ax называют главным направлением квадратичной формы.