
- •Курсовая работа
- •Обыкновенных дифференциальных уравнений и теории колебаний”
- •Содержание
- •Пояснительная записка
- •1. Найти особые точки системы. Определить их тип. Построить схематически фазовый портрет в окрестностях каждой особой точки.
- •2. Найти первый интеграл. Изобразить фазовый портрет уравнения на плоскости .
- •3. Исследовать при каких значениях параметра асимптотически устойчиво нулевое решение уравнения.
- •4. Исследовать устойчивость нулевого решения, построив функцию Ляпунова и применив теоремы Ляпунова или Четаева
- •5. С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость нулевое решение системы
- •6. Используя теорему Пуанкаре-Бендиксона, доказать существование цикла у системы.
- •7. Методом Пуанкаре найти приближенно периодические решения дифференциального уравнения
- •Периодическое решение будем искать в виде ряда по степеням малого параметра, то есть в виде
- •Список литературы:
3. Исследовать при каких значениях параметра асимптотически устойчиво нулевое решение уравнения.
![]()
Решение.
Мы имеем стандартный полином с коэффициентами
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]()
Составим для полинома матрицу Гурвица, и применим критерий Льенара-Шипара:
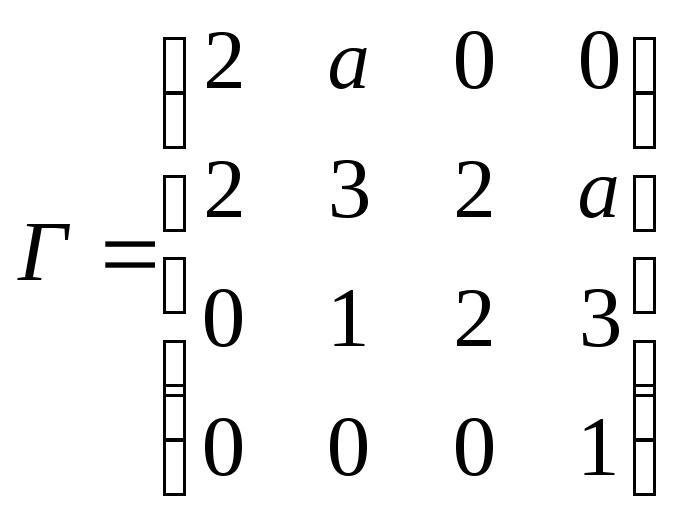
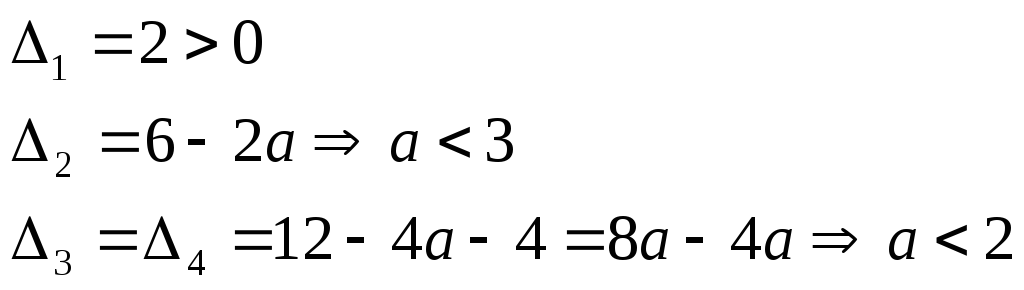
Следовательно,
система асимптотически устойчива при
![]() .
.
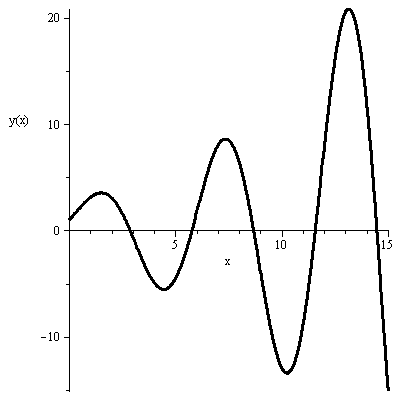
Проверим результат в пакете Maple:
>
![]()
>
![]()
>
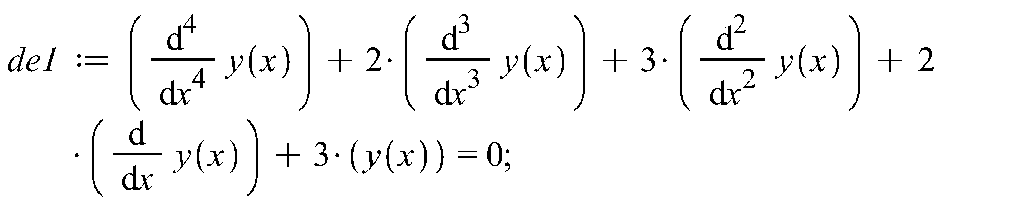

>
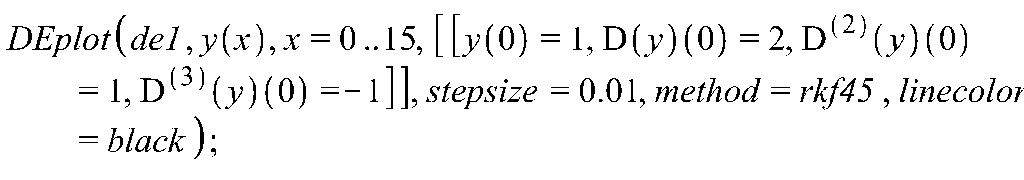
>
![]()

>
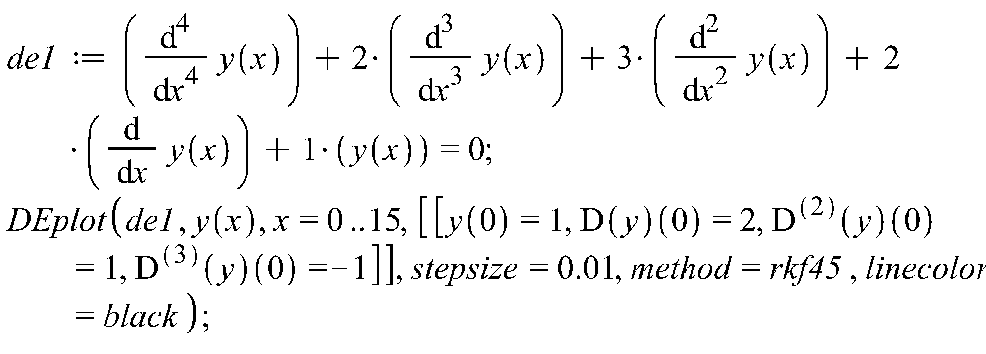
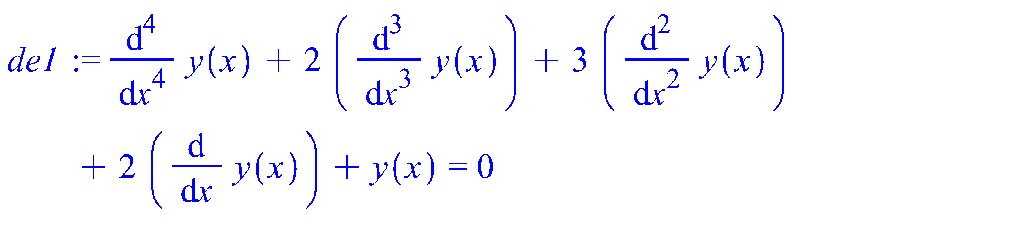
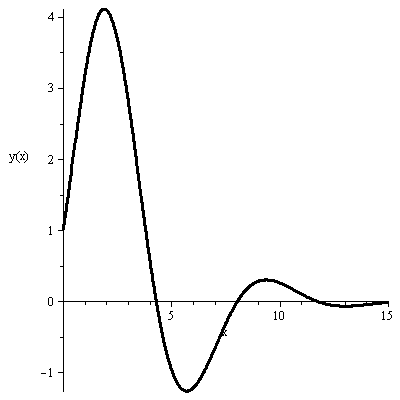
>
![]()

4. Исследовать устойчивость нулевого решения, построив функцию Ляпунова и применив теоремы Ляпунова или Четаева
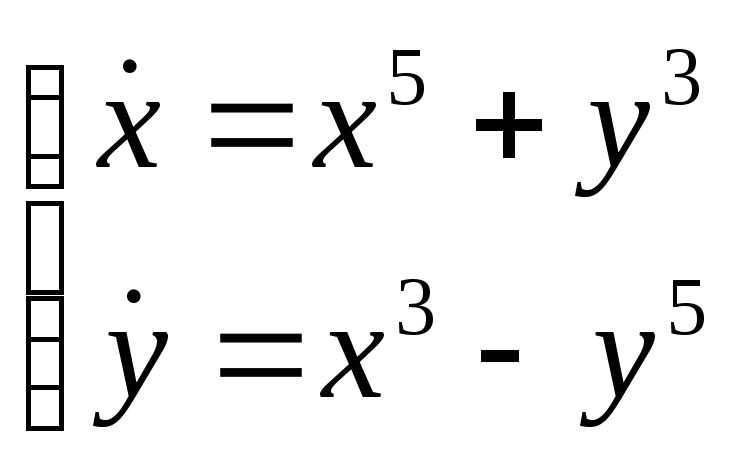
Решение.
Функцию Ляпунова
будем искать в виде
![]()
Тогда,
![]()
Положим,
![]() .
Функция Ляпунова и ее производная в
силу системы будут иметь вид:
.
Функция Ляпунова и ее производная в
силу системы будут иметь вид:
![]()
Зададим множество
![]()
Теорема 4
(теорема
Четаева).
Пусть
![]() –
положение равновесия системы
–
положение равновесия системы
![]() .
Пусть
.
Пусть
![]() -
непрерывно дифференцируемая функция,
такая что
-
непрерывно дифференцируемая функция,
такая что
![]() и
и
![]() для некоторой точки
для некоторой точки
![]() ,
такой что
,
такой что
![]() - произвольно малая величина. Определим
множество
- произвольно малая величина. Определим
множество
![]() ,
и предположим что
,
и предположим что
![]() в
в
![]() .
Тогда,
.
Тогда,
![]() -
неустойчивое положение равновесия
системы.
-
неустойчивое положение равновесия
системы.
Очевидно, что на
множестве
![]() (и
везде на плоскости) производная в силу
системы принимает положительные
значения. Положение равновесия неустойчиво
по теореме Четаева.
(и
везде на плоскости) производная в силу
системы принимает положительные
значения. Положение равновесия неустойчиво
по теореме Четаева.
Проверим полученный результат в пакете Maple (Рис. 4.1)
> restart: with(DEtools):
> eq1:=(diff(x(t),t)=(x(t)^5)+(y(t)^3));
![]()
> eq2:=(diff(y(t),t)=(x(t)^3)-(y(t)^5));
![]()
> DEplot([eq1,eq2],[x(t),y(t)],t=0..50,[[x(0)=0.35, y(0)=-0.39],[x(0)=-0.4, y(0)=0.35], [x(0)=-0.4, y(0)=0.45],[x(0)=0.4, y(0)=-0.4]],x=-0.5..0.5, y=-0.5..0.5, linecolor=sin(t), stepsize=0.01);

Рис. 4.1 Фазовый портрет системы
5. С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость нулевое решение системы
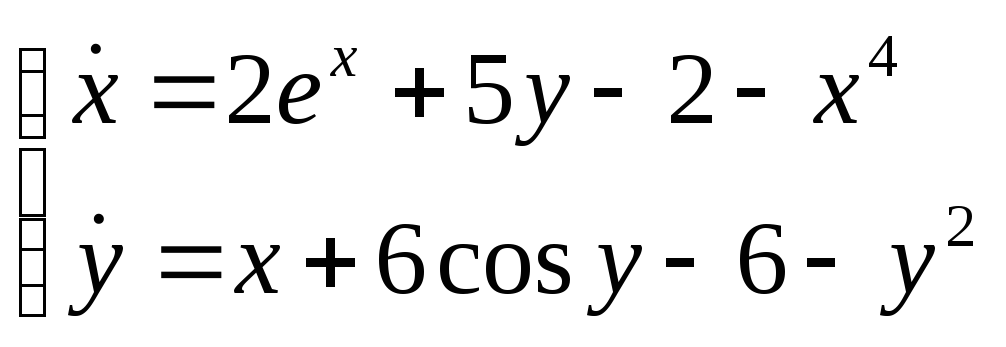
Решение.
Составим якобиан системы:
![]()
![]()
Теорема 5 (о
неустойчивости по первому приближению).
Пусть функция
![]() непрерывно
дифференцируема в некоторой окрестности
положения равновесия
непрерывно
дифференцируема в некоторой окрестности
положения равновесия
![]() .
Если хотя бы одно собственное значение
матрицы Якоби
.
Если хотя бы одно собственное значение
матрицы Якоби
![]() имеет положительную вещественную часть,
то положение равновесия
имеет положительную вещественную часть,
то положение равновесия
![]() неустойчиво
по Ляпунову.
неустойчиво
по Ляпунову.
Найдем собственные
значения матрицы
![]() :
:
![]()
Полином не является гурвицевым:
![]()
Мы имеем один положительное собственное значение, следовательно тривиальное решение системы неустойчиво по Ляпунову.
Проверим наш результат в пакете Maple (Рис. 5.1)
>
![]()
![]()
![]()
![]()
![]()
>
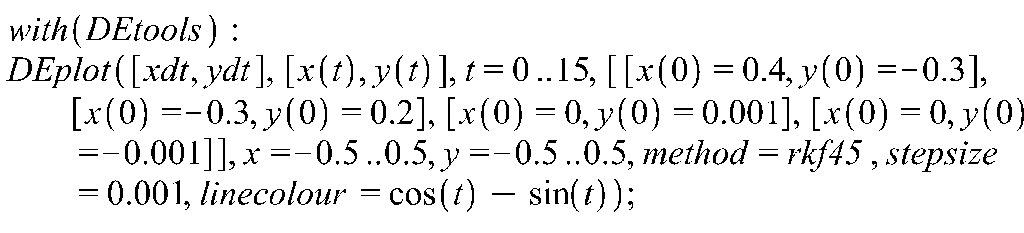
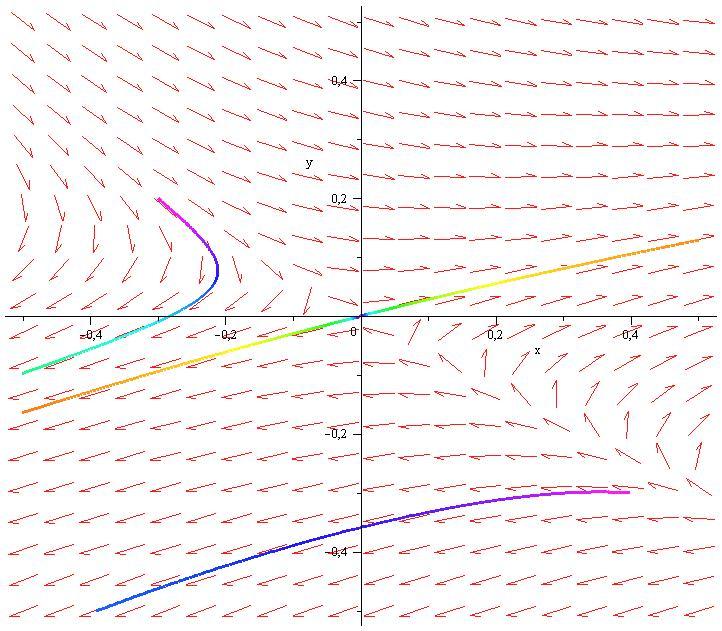
Рис. 5.1 Численное интегрирование системы
6. Используя теорему Пуанкаре-Бендиксона, доказать существование цикла у системы.
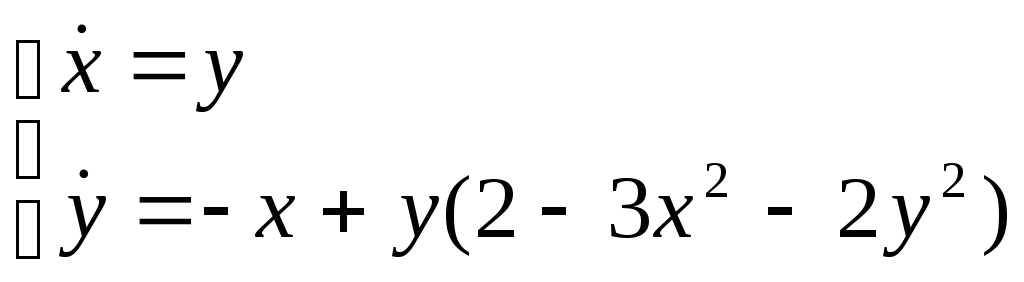
Решение.
Сначала, покажем что у системы существует единственное (неустойчивое) состояние равновесия.
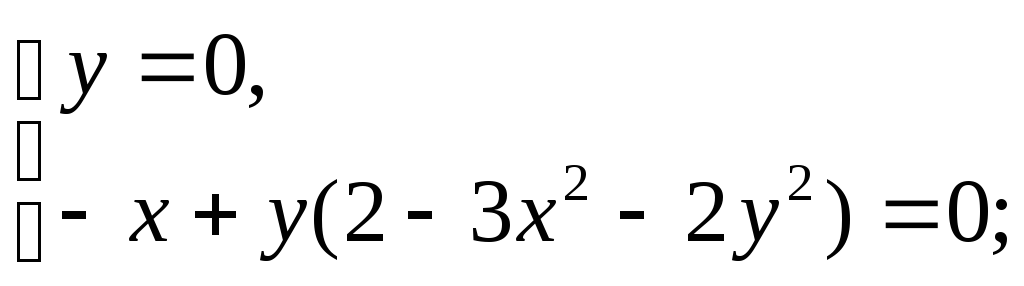
![]()
Построим якобиан системы:
![]() ;
;
![]() ;
;
Найдем собственные
значения
![]() :
:
![]() ,
,
![]() ,
,
![]()
Оба собственных значения якобиана положительны, особая точка неустойчива.
Рассмотрим функцию
![]()
Ее производная в силу системы имеет вид:
![]() ;
;
Значения производной в силу системы меняются при пересечении эллипса
|
|
(6.1) |
Однако, мы не можем
использовать эллипсы для доказательства
существования «кольца». Рассмотрим 2
окружности,
![]() ,
которая не пересекает эллипс (6.1) и лежит
внутри него, и окружность
,
которая не пересекает эллипс (6.1) и лежит
внутри него, и окружность
![]() ,
которая так же не пересекает заданный
эллипс, и внутри которой он располагается
(Рис. 6.1)
,
которая так же не пересекает заданный
эллипс, и внутри которой он располагается
(Рис. 6.1)
>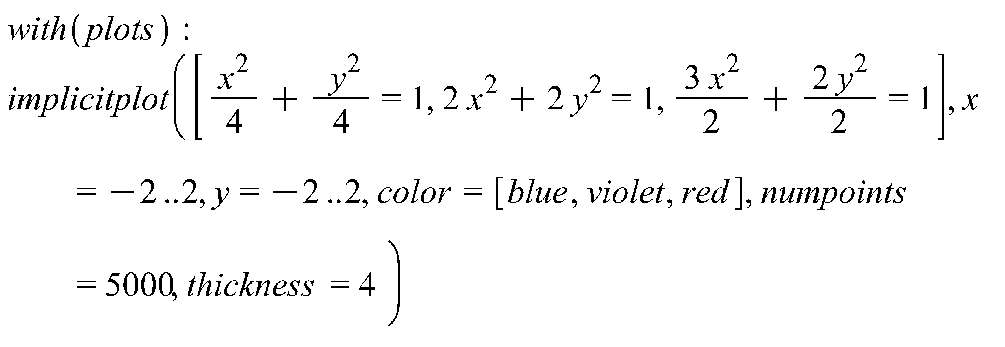
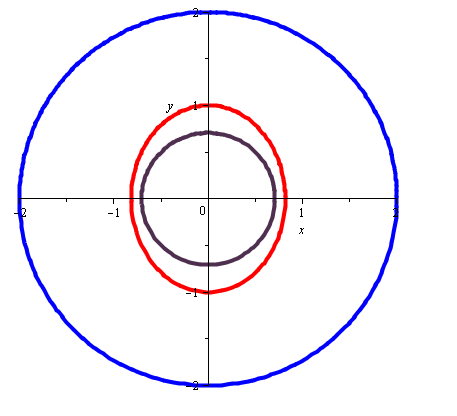
-
Рис. 6.1 Эллипс (1), при пересечении которого производная в силу системы меняет знак (красный), окружность
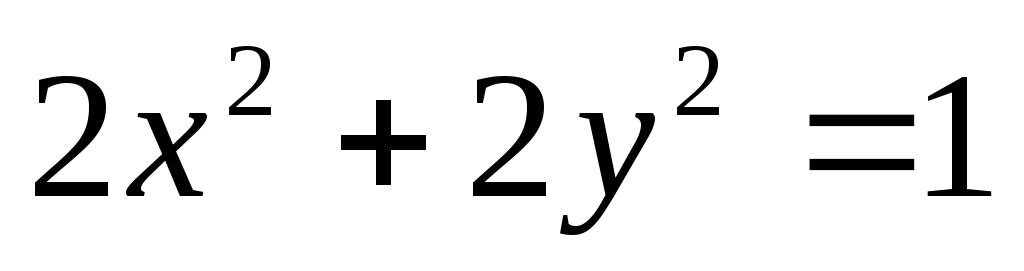 (фиолетовая), окружность
(фиолетовая), окружность
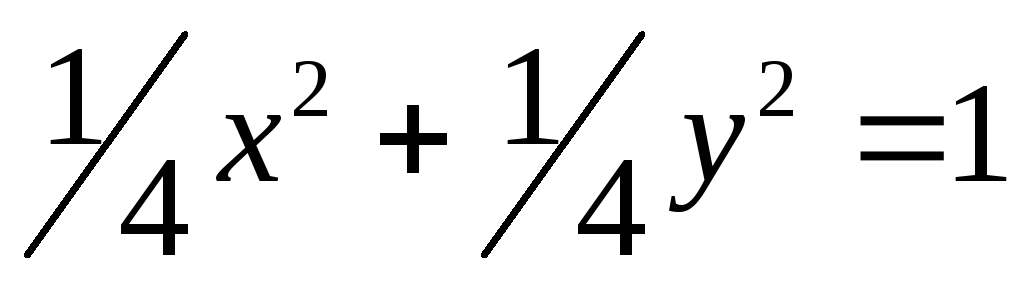 ,
(синяя).
,
(синяя).
На окружности
![]() производная в силу системы принимает
положительные значения, на
производная в силу системы принимает
положительные значения, на
![]() - отрицательные, то есть траектории
системы пересекают первую окружность
в направлении «от центра», и вторую
окружность по направлению «к центру».
- отрицательные, то есть траектории
системы пересекают первую окружность
в направлении «от центра», и вторую
окружность по направлению «к центру».
На каждой окружности возьмем точки, лежащие близко к оси абсцисс и проверим поведение траекторий. Расчеты будем производить при помощи пакета Maple:
>
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
Действительно, по теореме о непрерывной зависимости решений от начальных данных, траектории будут в дальнейшем вести себя подобным образом.
Мы можем заявить о существовании цикла у системы.
Лемма 6. Если
внутри положительно (отрицательно)
инвариантной для траекторий системы![]() области нет состояний равновесия
системы, то в этой области содержится
по крайней мере один цикл системы.
области нет состояний равновесия
системы, то в этой области содержится
по крайней мере один цикл системы.
Мы доказали, что у системы существует положительно инвариантная область, в которой нет решений системы. По лемме 6, у системы есть цикл.
Проверим полученный результат в пакете Maple (Рис. 6.2).
>
![]()
![]()
![]()
![]()
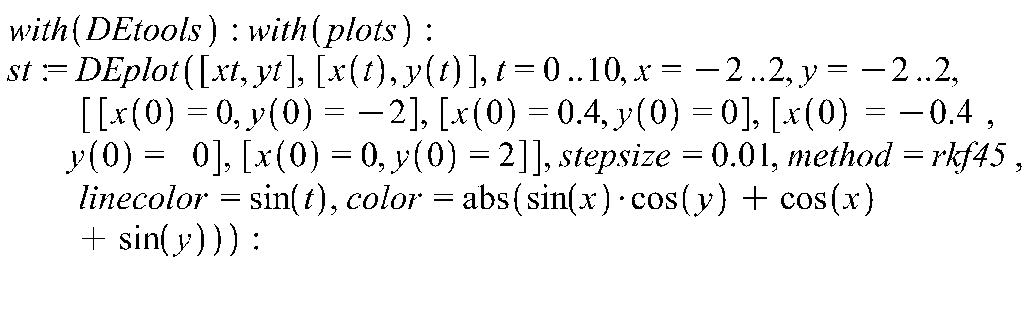
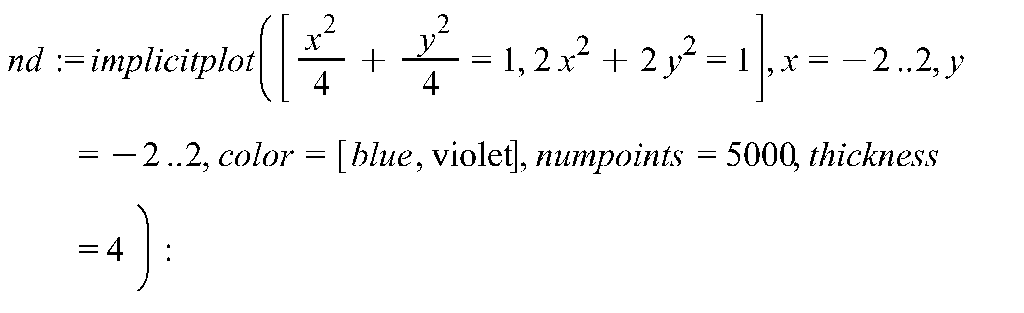
>
![]()
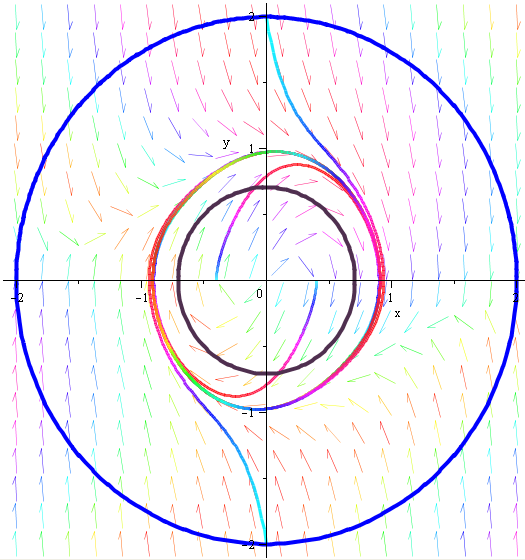
Рис. 6.2 Численное интегрирование системы
