
- •Курсовая работа
- •Обыкновенных дифференциальных уравнений и теории колебаний”
- •Содержание
- •Пояснительная записка
- •1. Найти особые точки системы. Определить их тип. Построить схематически фазовый портрет в окрестностях каждой особой точки.
- •2. Найти первый интеграл. Изобразить фазовый портрет уравнения на плоскости .
- •3. Исследовать при каких значениях параметра асимптотически устойчиво нулевое решение уравнения.
- •4. Исследовать устойчивость нулевого решения, построив функцию Ляпунова и применив теоремы Ляпунова или Четаева
- •5. С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость нулевое решение системы
- •6. Используя теорему Пуанкаре-Бендиксона, доказать существование цикла у системы.
- •7. Методом Пуанкаре найти приближенно периодические решения дифференциального уравнения
- •Периодическое решение будем искать в виде ряда по степеням малого параметра, то есть в виде
- •Список литературы:
2. Найти первый интеграл. Изобразить фазовый портрет уравнения на плоскости .
![]()
Решение.
Канонический вид уравнения Ньютона:
![]()
Оно описывает
движение материальной частицы массой
![]() ,
в потенциальном поле с потенциалом
,
в потенциальном поле с потенциалом ![]() .
В нашем случае, уравнение имеет вид:
.
В нашем случае, уравнение имеет вид:
![]()
где
![]() ,
а
,
а ![]() .
.
Для того, что бы
найти первый интеграл, умножим обе части
уравнения на
![]() :
:
![]() ,
,
следовательно:
![]()
![]()
Выражение является первым интегралом уравнения. Т.к. он является суммой кинетической и потенциальной энергии системы, этот интеграл называется интегралом энергии данной системы.
Полагая, что![]() ,
мы получаем эквивалентную исходному
уравнению систему:
,
мы получаем эквивалентную исходному
уравнению систему:
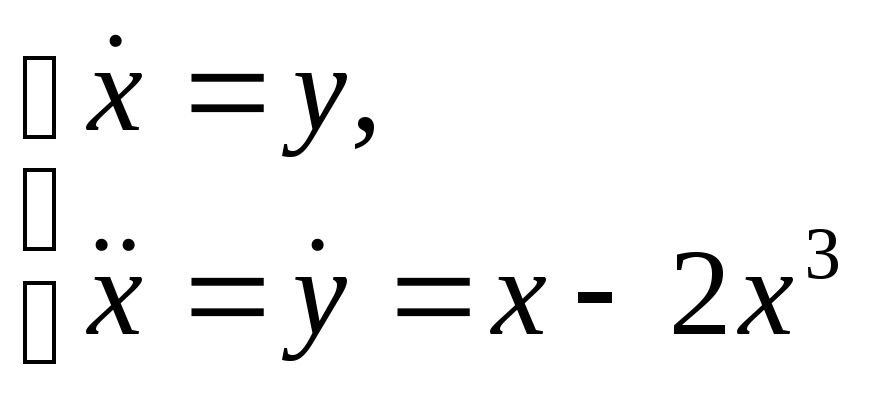
Найдем особые точки системы:
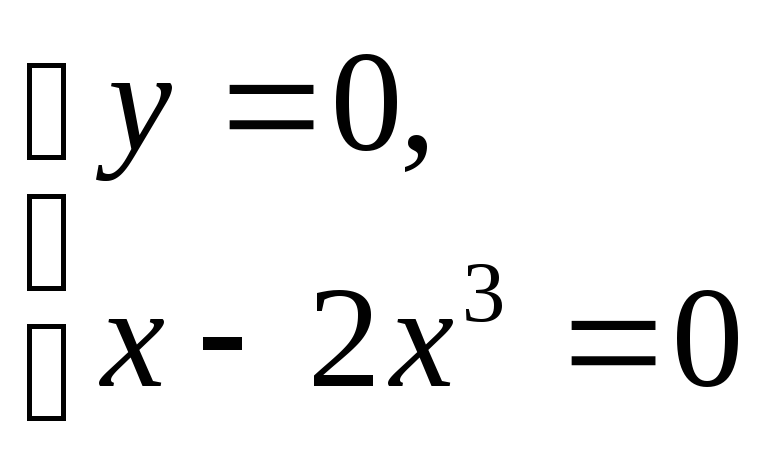
:
![]() ,
или
,
или
![]()
![]()
![]()
![]()
Таким образом, имеем три особые точки:
![]()
Исследуем функцию :
Функция четная, ;
![]()
![]()
Функция обращается в 0 при .
Производная функции обращается в ноль в особых точках системы.
![]() .
.
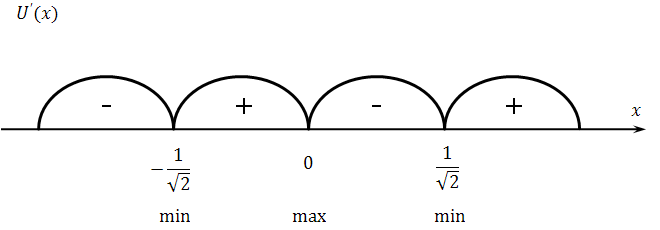
Таким образом,
особая точка
![]() -
точка типа «седло».
-
точка типа «седло».
и
![]() - точки типа
«центр».
- точки типа
«центр».
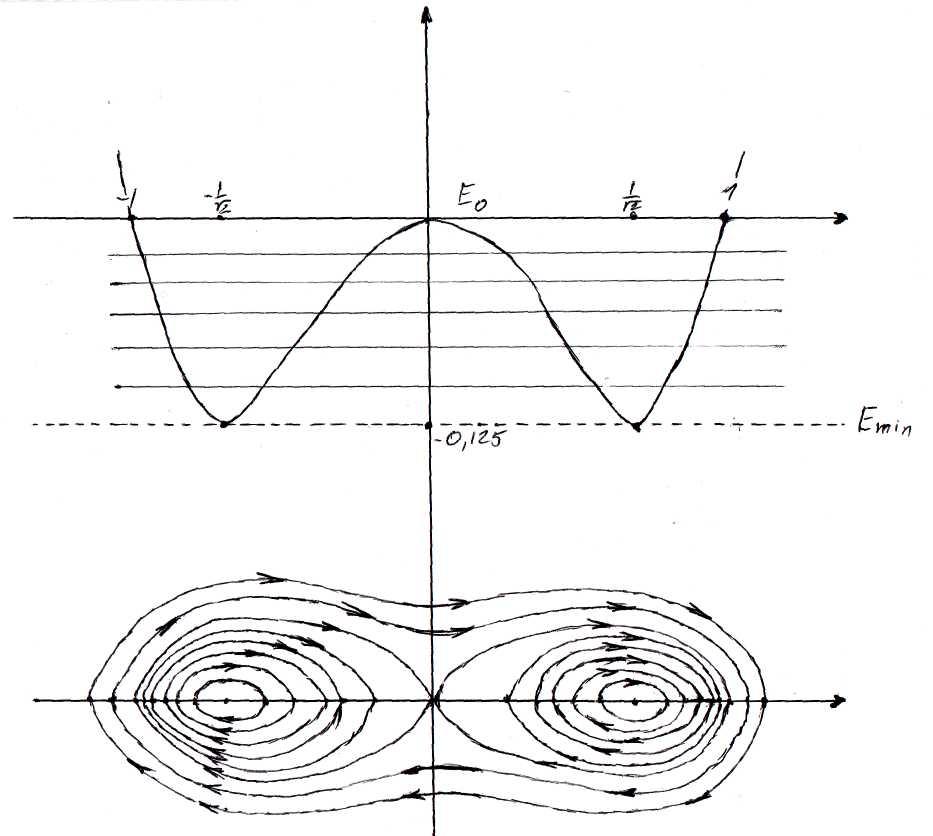
Рис 2.1 Фазовый
портрет уравнения на плоскости
![]() .
.
Проверим полученный результат в пакете Maple:
> restart; with(DEtools): >plot(((x^4)/2))- ((x^2)/2))),x=-2..2,y=-0.2..0.3) DEplot([diff(x(t),t)=y(t),diff(y(t),t)=x(t)-2*(x(t))^3], [x(t),y(t)], t=-10..10, [[x(0)=-2,y(0)=0], [x(0)=-1.5,y(0)=0], [x(0)=-1.25,y(0)=0], [x(1)=-1,y(1)=0],[x(1)=-0.75,y(1)=0], [x(1)=-0.5,y(1)=0], [x(1)=-0.25,y(1)=0],[x(0)=1,y(0)=0],[x(0)=0.75,y(0)=0], [x(0)=0.5,y(0)=0], [x(0)=0.25,y(0)=0]], x=-2..2, y=-4..4, stepsize=0.01, linecolour=red, method=rkf45);
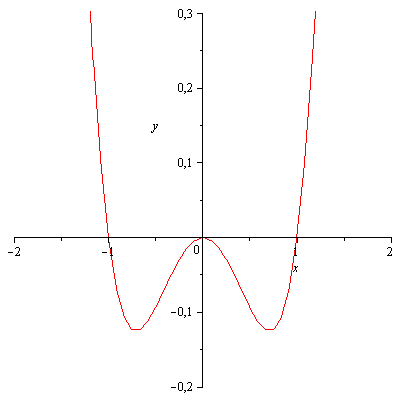
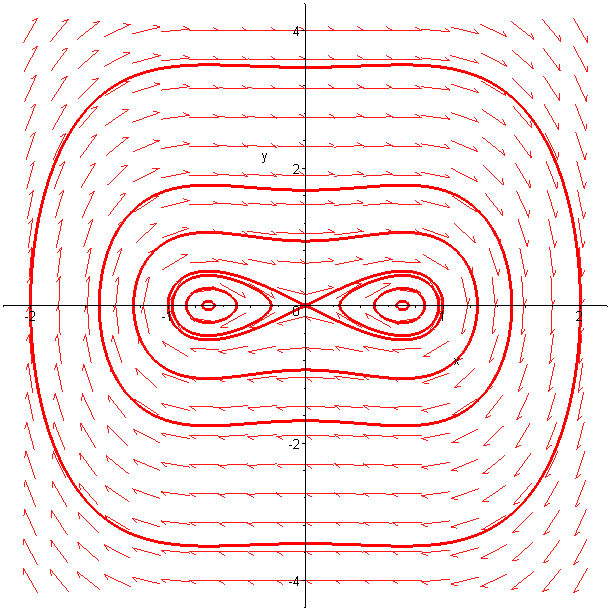
Рис 2.2 Фазовый
портрет уравнения на плоскости
![]() в пакете Maple.
в пакете Maple.
Угловые скорости движения точек по замкнутым фазовым траекториям (вокруг точек типа «центр») могут совпадать (синхронное движение) или же быть различным (асинхронное движение).
Для проверки
синхронности движения вокруг точек и
![]() вычислим периоды
движения по различным траекториям.
Воспользуемся формулой
вычислим периоды
движения по различным траекториям.
Воспользуемся формулой
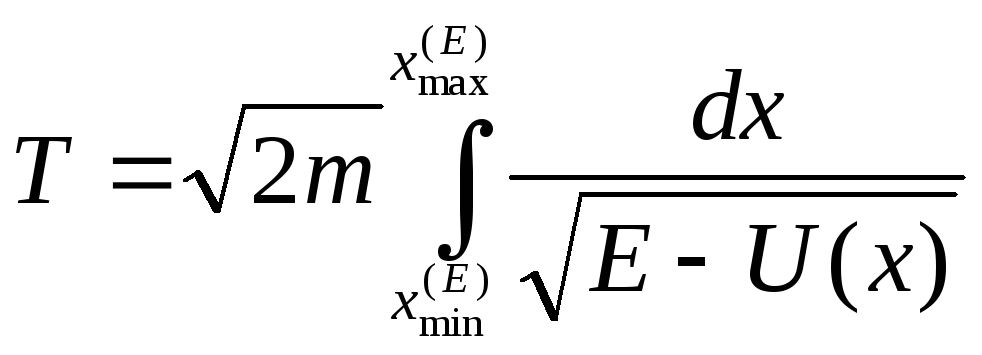
которая в нашем случае имеет вид:
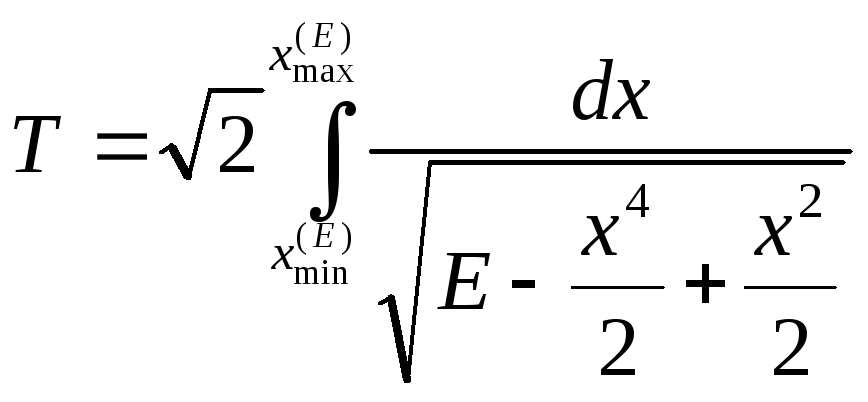
Варьируя уровень
энергии, построим таблицу зависимости
периода движения для точек и
![]() T+
и T-
соответственно.
T+
и T-
соответственно.
|
E |
-0.1 |
-0.08 |
-0.06 |
-0.04 |
-0.02 |
-0.01 |
|
T- |
4.132 |
4.276 |
4.328 |
5.042 |
5.578 |
6.638 |
|
T+ |
4.132 |
4.276 |
4.328 |
5.042 |
5.578 |
6.638 |
Таким образом, период вращения вокруг обеих точек зависит от уровня энергии (Рис 2.3), следовательно движение вокруг них является асинхронным.
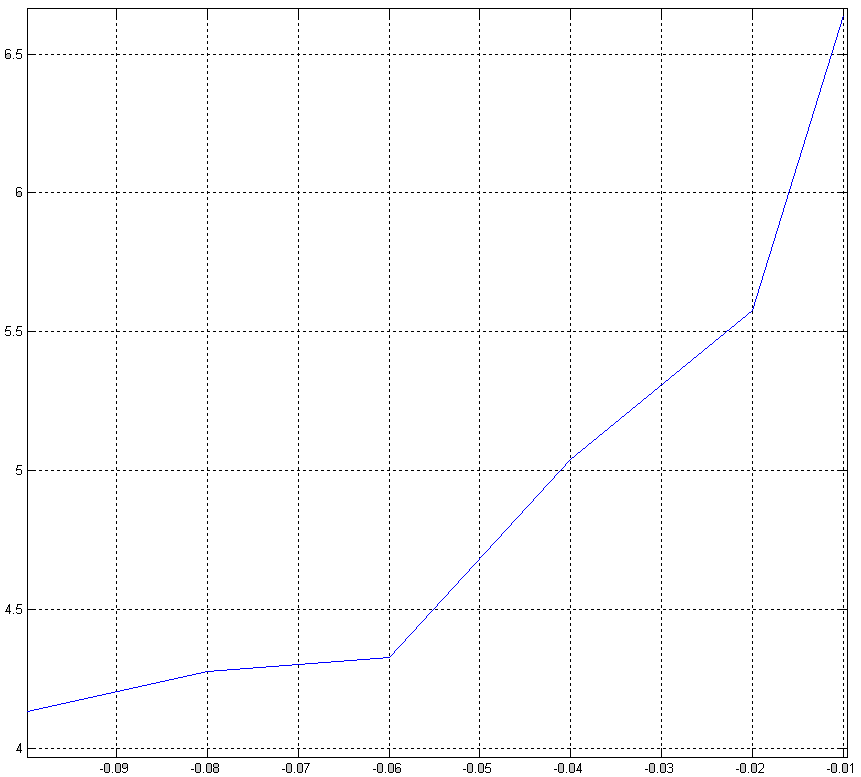
Рис 2.3 График
зависимости периода движения вокруг
точек и
![]() от уровня энергии.
от уровня энергии.
> E:=-(0.10);
evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
![]()
![]()
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.85..-0.53));
b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.53..0.85));
![]()
![]()
> E:=-(0.08);
evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
![]()
![]()
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.89..-0.45));
b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.45..0.89));
![]()
![]()
> E:=-(0.06);
evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
![]()
![]()
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.92..-0.38));
b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.38..0.92));
![]()
![]()
> E:=-(0.04);
evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
![]()
![]()
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.955..-0.3));
b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.3..0.955));
![]()
![]()
> E:=-(0.02);
evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
![]()
![]()
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.9789..-0.21));
b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.21..0.9789));
![]()
![]()
> E:=-(0.01);
evalf(solve( (((x^4)/2) -((x^2)/2) - E) , x),10);
![]()
![]()
> a:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=-0.9897..-0.143));
b:=simplify((2^(1/2))*int((1/(sqrt(E+(x^2)/2 - (x^4)/2))),x=0.143..0.9897));
![]()
![]()
