Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сыктывкарский Государственный Университет им. Питирима Сорокина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lok_extr

.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

454.81 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Определение. Точка x		называется точкой локального максимума функции	f x , если существует такая
	0
окрестность точки x0	, что для всех x из этой окрестности f x f x0 .
Определение. Точка x		называется точкой локального минимума функции	f x , если существует такая
	0
окрестность точки x0	, что для всех x из этой окрестности f x f x0 .

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Максимум и минимум функции называются её локальными экстремумами.

Термин "локальный экстремум" обусловлен тем, что введённое понятие экстремума связано с окрестностью данной точки в области определения функции, а не со всей этой областью. Функция может иметь несколько экстремумов, причём минимум в одной точке может быть больше максимума в другой.

Обычно в литературе используют термины "экстремум", "максимум", "минимум" для обозначения строгого локального экстремума, строгого локального максимума, строгого локального минимума.

Определение. Точка x	называется точкой строгого локального максимума функции	f x , если существует
0
такая окрестность точки x0 , что для всех x из этой окрестности f x f x0 .
Определение. Точка x	называется точкой строгого локального минимума функции	f x , если существует
0

такая окрестность точки x0 , что для всех x из этой окрестности f x f x0 .

Или, точка x0 называется точкой строгого локального минимума функции f x , если

0 x: 0 x x0 f x f x0 .

Определение. Наибольшее (наименьшее) значение функции на промежутке называется глобальным экстремумом. Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

Матрица, составленная из вторых производных функции, называется матрицей Гессе:

			2 f x		2 f	x
				...
			x2	...	x1 xn
			x2		x1 xn
d 2 f x			1
d 2 f x
			...	...	...
dx	T	dx	...	...	...
dx		dx	2 f x		2 f	x
			2 f x		2 f	x
				...
			x x	...
			x x		x	2
			n 1		x
						n

(гессианом условимся называть определитель матрицы Гессе; аналогично: матрица, составленная из первых производных функции, называется матрицей Якоби, а её определитель называется якобианом.

Литература:

1)Малугин В.А. "Математический анализ, курс лекций (математика для экономистов)", 2005, стр. 105 (понятие экстремума функции);

2)Малугин В.А. "Математический анализ, задачи и упражнения (математика для экономистов)", 2006, стр. 132 (глобальный экстремум; необходимое условие экстремума, 1-е и 2-е достаточное условие экстремума);

3)Письменный Д.Т. "Конспект лекций по высшей математике", 2005, стр. 202 (экстремум функции одной переменной);

4)Бортаковский А.С., Пантелеев А.В. "Линейная алгебра в примерах и задачах", 2005, стр. 226.

Краткое оформление решения задачи.

Теорема (достаточное условие экстремума). Пусть в стационарной точке x0 , y0 и некоторой её

окрестности функция

f x, y

имеет непрерывные частные производные до второго порядка включительно.

Вычислим в точке x0 , y0 значения

fxx x0 , y0 , B

fxy x0 , y0 ,

C fyy x0 , y0 .

Обозначим

AC B 2

, тогда:

1) если 0 , то функция

x , y

в точке x0 , y0

имеет экстремум: максимум, если A 0 ;

минимум, если A 0 ;

x , y

в точке x0 , y0

2) если 0 , то функция

экстремума не имеет.

В случае 0

экстремум в точке x0 , y0 может быть, может не быть. Необходимы дополнительные

исследования.

1) Исследовать на экстремум функцию

z x y

20 ,

x 0 ,

y 0

x y

Находим стационарные точки:

zx 0zy 0

y x502 0

x y 2 0

x 5y 2

Найдена стационарная точка P 5; 2 . Проверим выполнение достаточных условий наличия экстремума в данной точке.

	50

A zxx y	x	2
			x
	50

B zxy y	x	2
			y
	20

C zyy x
	y	2
			y

100x 3

40y 3

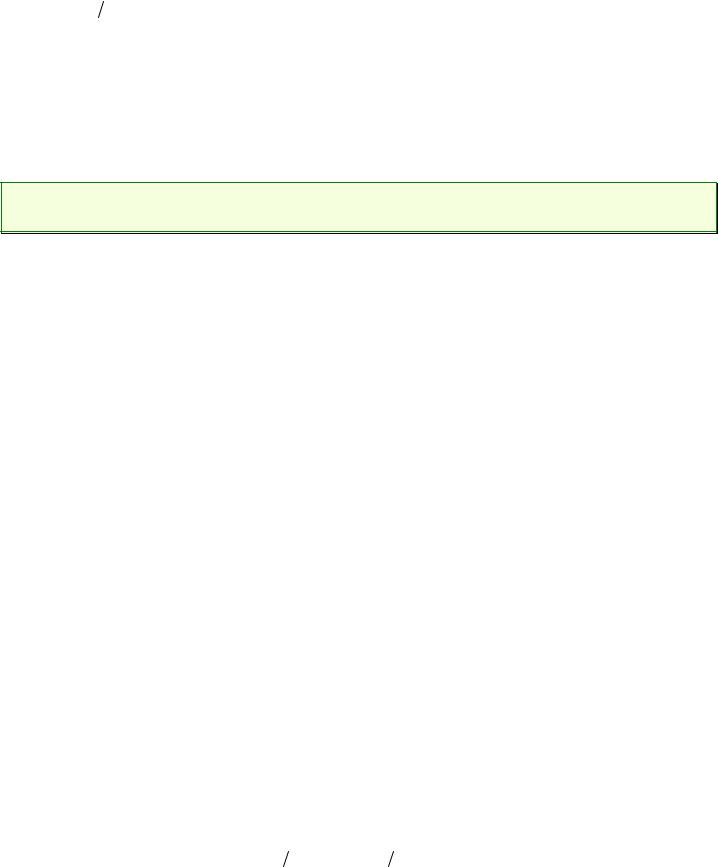
В точке P 5; 2 :

A 4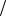5 0

B 1

C 5

	4 5	1	3 0
	4 5	1	3 0
	1	5
- в точке P 5; 2				A 0	. Значение функции в этой точке	z 5; 2 30 .
- в точке P 5; 2		минимум, т.к.		0	. Значение функции в этой точке	z 5; 2 30 .
				0

Ответ: функция имеет минимум z 5; 2 30 .

2) Найти экстремумы функции z xy 2 1 x y

z xy 2 x 2 y 2 xy 3

zx y 2 2xy 2 y 3

zy 2xy 2x 2 y 3xy 2

2x y 0

xy 2 2x 3 y 0

y 0

2x y 0

x 0

2x 3 y 0

Заметим, что при y 0

решением является множество точек с координатами x R (в пространстве это

y 0

, параллельная оси Ox ). Следовательно, среди точек с y 0 стационарных точек нет.

прямая

z 0

Исключая точки с y 0 из рассмотрения, получаем:

1 2x y 0

x 0

3 y 0

2 2x

1 2x y 0

1 2x y

x 0

2 2x 3 y

1 y 0

1 2 y 0

y 1

y 1 2

x 1 4

; 1

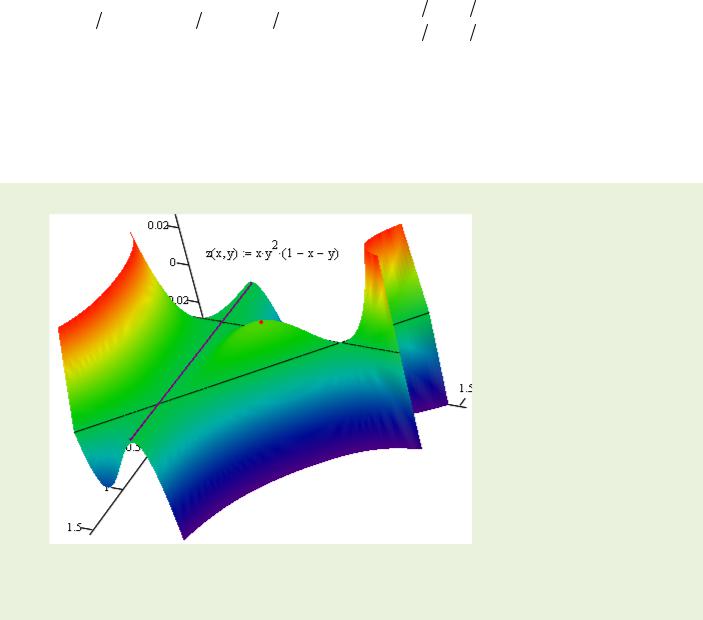
Найдены две стационарные точки	P	0; 1 и	P	1		;	1	; проверим их на соответствие достаточному
	1		2		4		2
					4		2

условию наличия экстремумов в данных точках.

A zxx 2 y 2

Bzxy 2 y 4xy 3 y 2

Czyy 2x 2x 2 6xy

Вточке P1 0; 1 :

A 2 0 ,	B 1,	C 0 ,	A B	2	1	1 0

			B C	1	0

Поскольку 0 , то в данной точке экстремума нет.

Вточке P2 1 ; 1 :

4 2

A 1 2 0 , B 1 4,			C 3 8 ,						A B	1 2		1 4			1	0
A 1 2 0 , B 1 4,			C 3 8 ,						A B	1 2		1 4			1	0
									B C	1 4		3 8			8
	A 0									1			1	1
Поскольку	0	, то в данной точке функция имеет максимум z										;			.
Поскольку		, то в данной точке функция имеет максимум z									4	;	2	64	.
											4		2	64
				1		1	1
Ответ: функция имеет максимум			z		;			.
Ответ: функция имеет максимум			z	4	;	2	64	.
				4		2	64

Сделаем иллюстрацию в Mathcad 14:

y 0	выделена бордовым цветом; пересечение
- найденный максимум отмечен красной точкой; прямая	выделена бордовым цветом; пересечение
z 0
чёрных прямых происходит в точке P1 0; 1 .

3) Исследовать функцию на экстремум z x 3 3x y 2 15x 12 y .

zx x 3 3x y 2 15x 12 y x 3x 2 3 y 2 15 zy x 3 3x y 2 15x 12 y y 6xy 12

Находим стационарные точки:

zx 0zy 0

3x 2 3 y 2 15 0

6xy 12 0

x 2 y 2 5

xy 2

x 2 y 2 5

y 2x

- окружность в пересечении с гиперболой даст четыре точки:

x		1	2
		1
			1
	y1		1

	x	2	1
		2
			2
	y 2		2

	x	3	1
		3
			2
	y 3		2

x		4	2
		4
			1
	y 4		1

Найдены четыре стационарных точки P1 2; 1 ,				P2 1; 2 ,	P3 1; 2 , P4 2; 1 . Проверим

выполнение достаточных условий наличия экстремума в данных точках.

	2		2
		3 y		15	x	6x
A zxx 3x
	2		2
		3 y		15	y	6 y
B zxy 3x

Czyy 6xy 12 y 6x

►В точке P1 2; 1 :

A 12 0

B 6

C 12

A	B	12	6	144 36 108 0
A	B	12	6	144 36 108 0
B	C	6	12

- в точке P 2; 1				максимум, т.к. A 0 . Значение функции в этой точке z 2; 1 28 .
1
								0
► В точке P2 1; 2 :
A 6 0
B 12
C 6
	A	B			6	12		36 144 108 0
	A	B			6	12		36 144 108 0
	B	C			12	6
- в точке P2 1; 2				нет экстремума, т.к. 0 .
► В точке P3 1; 2 :
A 6 0
B 12
C 6
	A	B			6	12	36 144 108 0
	A	B			6	12	36 144 108 0
	B	C			12	6
- в точке P3 1; 2			нет экстремума, т.к. 0 .

► В точке P4 2; 1 :

A 12 0

B 6

C 12

	A	B		12	6	144 36 108 0
	A	B		12	6	144 36 108 0
	B	C		6	12
- в точке P	2	; 1	минимум, т.к.				A 0	. Значение функции в этой точке z 2; 1 28 .
4
							0

Ответ: функция имеет минимум z 2; 1 28 и максимум z 2; 1 28 .

Литература:

1) Письменный Д.Т. "Конспект лекций по высшей математике", 2005, стр. 320...323 (экстремум функции двух переменных).

Решение задачи с использованием матрицы Гессе.

4) Найти экстремумы функции двух переменных z x , y 3x 2 2 y 3 6xy 12x

Определим стационарные точки из условия

z 0x

z 0y

(необходимое условие существования экстремума)

3x 2

2 y 3

6xy 12x

6x 6 y 12

2 y

6xy 12x

6 y

6x 6 y 12 0

6 y 2 6x

x y 2

y2 x

y1 1

Точки P1 1; 1

и P2 4; 2 - стационарные точки; проверим их на соответствие достаточному условию

наличия экстремума. Для этого из вторых производных функции составим матрицу Гессе:

2 z

Hx2

2 zy x

2 zx y2 zy2

	2	z	6
		z	6
x2
	2					6	6
z						6	6
z				6	H
x y				6	H	6
x y						6	12 y
2 z
2 z			12 y
y		2	12 y
y

► Продолжение решения через анализ угловых миноров матрицы Гессе [1]

Рассмотрим поведение матрицы Гессе в найденных стационарных точках.

P1	1; 1 :	H P1	6	6
P1	1; 1 :	H P1	6	12		;
			6	12
	угловые миноры: M1 6 0				,

M2 6 12 6 6 108 0 .

Поскольку M2 0 , то в точке P1 экстремума нет.

P2 4; 2 :					6	6
	H P2			6		24	;

угловые миноры: M1 6 0 ,
M2 6 24 6 6 108 0 .
	M	1	0		, то в точке P2 функция имеет локальный минимум z 4; 2 32 .
Поскольку
	M2			0

Теорема (достаточные условия экстремума). Если в некоторой точке выполнены необходимые условия экстремума и все частные производные 2-го порядка непрерывны, то существование экстремума в этой точке определяется значениями угловых миноров матрицы вторых производных (матрицы Гессе):

M1 0 , M2 0 - локальный минимум;

M1 0 , M2 0 - локальный максимум; M2 0 - экстремума нет.

Если M1 0 или M2 0 экстремум в исследуемой точке может быть, может не быть - необходимы дополнительные исследования.

При исследовании на локальный экстремум функции трёх переменных u u x , y , z рассматривается матрица

u xxu yxu zx

u xy u xz u yy u yz u zy u zz

и изучаются её угловые миноры.

Литература:

1)Малугин В.А. "Линейная алгебра. Задачи и упражнения", 2006, стр. 149 (локальный экстремум функции);

2)Письменный Д.Т. "Конспект лекций по высшей математике", 2005, стр. 320...323 (экстремум функции двух переменных);

3)Пяткова В.Б., Рузаков В.Я., Турова О.Е. "Математика, 3-й семестр", методичка УрГГУ (горный институт, Екатеринбург), 2005, стр. 23 (схема исследования функции двух переменных на экстремумы).

► Продолжение решения через анализ собственных значений матрицы Гессе [3]

Найдём собственные значения матрицы Гессе в каждой стационарной точке.

P1 1; 1 :	H P1	6	6
P1 1; 1 :	H P1	6	12
		6	12

Из уравнения

находим 1, 2 3 3

13 . Поскольку собственные значения матрицы

Гессе разных знаков, то в точке P1 экстремума нет.

P2 4; 2 :

H P2

Из уравнения

0 находим 1, 2 15 3

13 . Поскольку все собственные значения

матрицы Гессе положительные, то в точке P2 локальный минимум z 4; 2 32 .

Находим собственные значения матрицы Гессе в каждой из стационарных точек x* функции.

Если все собственные значения

► положительные:

i 0,

i 1,..., n , то в точке x* локальный минимум;

► отрицательные:

i 0,

i 1,..., n , то в точке x* локальный максимум;

► неотрицательные: i 0,

i 1,..., n , то в точке x* может быть локальный минимум;

► неположительные: i 0,

i 1,..., n , то в точке x* может быть локальный максимум;

►разных знаков, то в точке x* нет экстремума;

►нулевые: i 0, i 1,..., n , то требуется дополнительное исследование.

Литература:

1)Бортаковский А.С., Пантелеев А.В. "Линейная алгебра в примерах и задачах", 2005, стр. 530, стр. 531 (пример 9.8).

5)Найти точки экстремума функции

zx 2 40xy 2 xy 1 .

► Определим стационарные точки функции двух переменных z x, y из условия

zx 0zy 0

(необходимое условие существования экстремума)

zx 412 x 40 y 2 y zy 80xy x

2 x 40 y 2 y 0

80xy x 0

x		1	0
		1
			0
	y1		0

	x	2	0
		2
			1 40
	y 2		1 40

	x	3	41 320
		3
			1 80
	y 3		1 80

Найдены три стационарные точки P1 0; 0 , P2 0; 1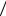40 , P3 41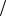320; 1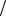80 ; проверим их на соответствие достаточному условию наличия экстремума.

При исследовании на локальный экстремум функции двух переменных z z x, y составляется матрица квадратичной формы функции относительно дифференциалов dx , dy - матрица Гессе


zxx		zxy

	zyx	zyy
	zyx	zyy

и рассматривается в каждой стационарной точке Pi .

► Если эта квадратичная форма окажется определённой, то функция z z x, y в точке Pi имеет

экстремум:

а) минимум, если квадратичная форма положительно определённая; б) максимум, если квадратичная форма отрицательно определённая.

►Если же квадратичная форма окажется неопределённой, то в точке Pi экстремума нет.

►В случаях неотрицательной определённости или неположительной определённости квадратичной формы требуется дополнительное исследование - экстремум может быть.

► Матрица Гессе:
	2 z			2 z
	x2
				x y
H				x y
H		2	z		2	z
			z			z
	y x			y		2
	y x			y

x 40 y 2

80 y 1

x y

80xy x

80x

(Заметим, что 2 F 2F 80 y 1 ).

x y y x

Итак,

	2 41	80 y 1
H	80 y 1	80x

►Установим знакоопределённость квадратичной формы, используя критерий Сильвестра [1].

►Для того, чтобы квадратичная форма от n переменных была положительно определённой, необходимо и достаточно, чтобы все угловые миноры её матрицы A были положительными.

►Для того, чтобы квадратичная форма от n переменных была отрицательно определённой, необходимо и

достаточно, чтобы знаки угловых миноров матрицы A квадратичной формы чередовались, начиная со знака минус.

►Для неопределённости (знакопеременности) квадратичной формы достаточно, чтобы хотя бы один главный минор чётного порядка был отрицателен, либо два главных минора нечётного порядка имели бы разные знаки (достаточный признак неопределённости квадратичной формы).

►В стационарной точке P1 0; 0 :

H P1	2 41		1
		1	0

угловые миноры: M1 241 0 ,

M2	2 41	1	0 1 1 0 ,
M2	2 41	1	0 1 1 0 ,
	1	0

-квадратичная форма знаконеопределённая, следовательно, в точке P1 экстремума нет.

►В стационарной точке P2 0; 1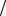40 :

H P2		2 41		1
H P2		1		0
		1		0
	угловые миноры:					M1 2 41 0 ,
	M2		2 41		1	0 1 1 0 ,
	M2		2 41		1	0 1 1 0 ,
			1		0

- квадратичная форма знаконеопределённая, следовательно, в точке P2 экстремума нет.

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.07.2019162.82 Кб45Literatura_po_UMK.doc
#
24.04.2019111.27 Кб14lkz gtnhjuhfabb.docx
#
29.03.20161.09 Mб38logica.pdf
#
26.11.2018180.22 Кб10Logika_i_teor_arg2011_OZO.doc
#
28.03.2016327.68 Кб23Logika_sots_rab_OZO_2012.doc
#
29.03.2016454.81 Кб7Lok_extr.pdf
#
02.12.2018640 Кб31make.doc
#
28.03.2016229.89 Кб7Makroekonomika_praktika.doc
#
15.09.20191.35 Mб20marKetING_(spora)_red.doc
#
28.03.2016709.12 Кб214Meditsina.doc
#
03.11.2018645.12 Кб10mem_teacher.DOC