
|
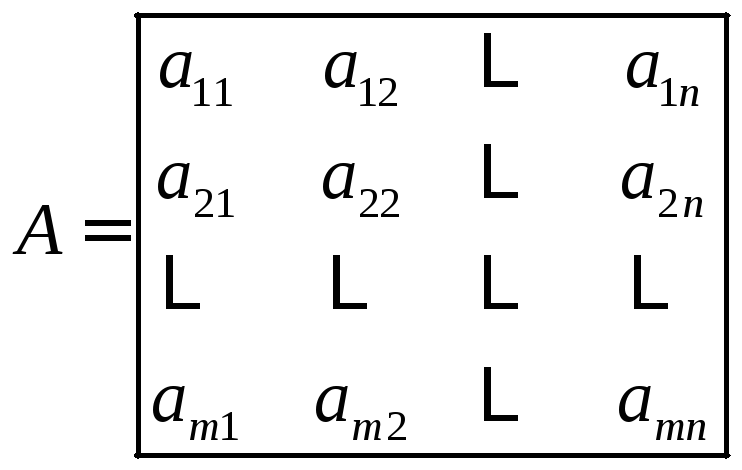
МАТРИЧНЫЕ ИГРЫ ОСНОВНЫЕ ПОНЯТИЯ Игра – упрощенная модель конфликта, имеющая четкие правила: варианты действий игроков, объем информации о действиях противника, выигрыш (исход конфликта), к которому приводит совокупность действий игроков. Игроки – стороны, участвующие в игре: 2 игрока – парная игра, более 2 – множественная игра (рассматриваются парные игры). Игра с нулевой суммой (антагонистическая игра) – выигрыш одного из игроков равен проигрышу другого. Стратегия игрока – совокупность правил, определяющих действия игрока при каждом личном ходе в зависимости от сложившейся ситуации. Решение антагонистической игры – выбор стратегий, удовлетворяющих условию оптимальности (игрок А должен получать максимальный выигрыш,когда игрок В придерживается своей стратегии, а игрок В должен получать минимальный проигрыш, когда игрок А придерживается своей стратегии). Устойчивость оптимальных стратегий – ни одному из игроков не выгодно отклоняться от своей оптимальной стратегии. Игра с полной информацией – перед каждым ходом каждый игрок знает все предшествующие ходы и выигрыши. Кооперативная игра – допускается возможность предварительных переговоров между игроками (рассматриваются некооперативные игры). МАТРИЦА ИГРЫ (платежная матрица) Пусть
у игрока
(Стратегии
игрока
Биматричная игра – у каждого из игроков своя платежная матрица. Матричная
игра
– интересы игроков противоположны
(выигрыш игрока
В
этом случае можно ограничиться одной
матрицей – матрицей игрока
СЕДЛОВАЯ ТОЧКА МАТРИЦЫ ИГРЫ
Очевидно,
что
Е Соответствующие цене игры стратегии – оптимальные чистые стратегии, а сама игра – игра с седловой точкой.
Если
СМЕШАННЫЕ СТРАТЕГИИ – применение своих чистых стратегий с частотами, задаваемыми
векторами
Оптимальные
смешанные стратегии
ТЕОРЕМА (Дж.ф. Нейман): Каждая конечная матричная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий. |
ПРИМЕРЫ
1. Пример игры Игроки А и В одновременно и независимо друг от друга записывают натуральные числа.Если их сумма четна, то единицу выигрывает игрок А (игрок В проигрывает единицу), если нечетна, то столько же выигрывает игрок В (игрок А единицу проигрывает). Матрица игры имеет вид:
B1 B2 A1 1 -1 A2 -1 1
2. Седловая точка платежной матрицы.
B1 B2 B3
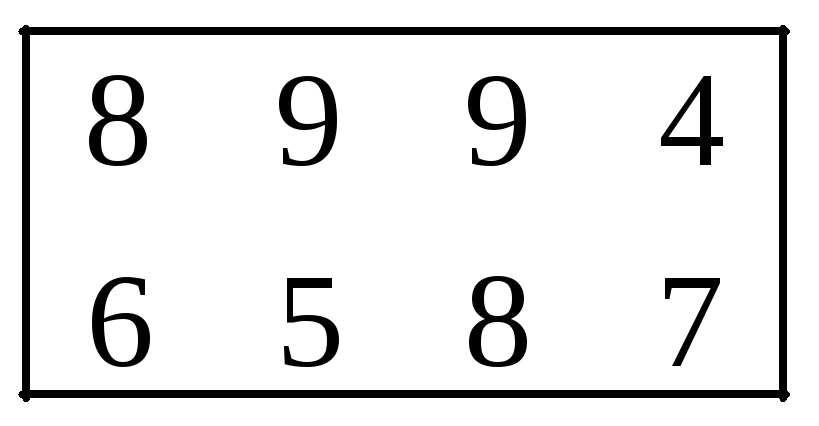
A1 4 5 3 3 A2 6 7 4 4 A3 5 2 3 2
6 7 4
Нижняя цена игры
Верхняя цена игры
Цена игры
3. Смешанные стратегии
Для игры из 1.
q 1-q p 1 -1 1-p -1 1
|
Теория игр матричные игры (продолжение)
|
ДУБЛИРОВАНИЕ И ДОМИНИРОВАНИЕ СТРАТЕГИЙ Дублирование стратегий – из одинаковых строк (столбцов) оставляем одну (один). Доминирование
стратегий
– если одна строка поэлементно больше
либо равна другой, удаляем меньшую.
Это же правило (со знаком
СВЕДЕНИЕ МАТРИЧНОЙ ИГРЫ К ЗАДАЧЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Р
Припишем
строкам вероятности
Вводя
новые переменные
Аналогично,приписывая
столбцам матрицы вероятности
Любую из этих задач можно решить одним из алгоритмов симплекс-метода, а затем, на основание теории двойственности, найти решение другой задачи. В
|
ПРИМЕРЫ
4
У
П
5.
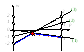
Графический
способ решения игр
И
Решая уравнения (1) и(3) получаем p =2/5, (1- p) =3/5 и v = w(2/5)= –2/5. Оптимальная
стратегия игрока А:
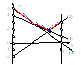
Первому столбцу припишем ненулевую вероятность q, а третьему – (1- q). Второму столбцу будет соответствовать нулевая вероятность. Решая систему
находим
q
= 4/5 и (1- q)
= 1/5. Оптимальная стратегия игрока В:
И
q
Ненулевые вероятности p и (1-p) припишем 1-й и 2-й строке. Решая полученную систему, находим p =5/8, (1- q) =3/8 Оптимальные стратегии: Игрок
А –
Игрок
В –
|


 сли
сли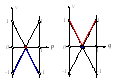 –оптимальная
чистая стратегия игрока
–оптимальная
чистая стратегия игрока
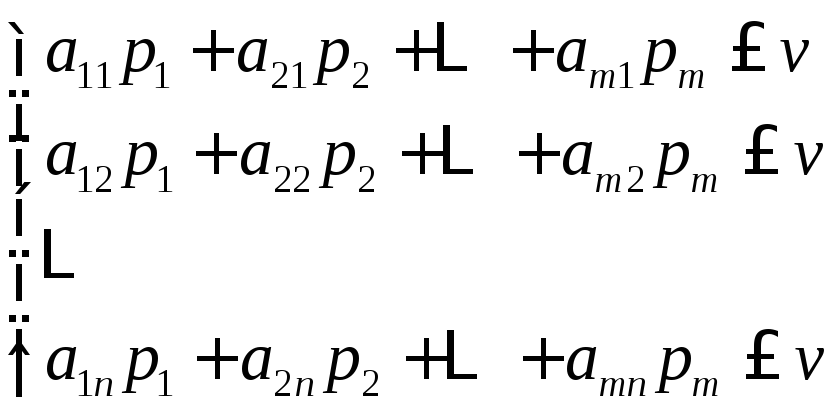
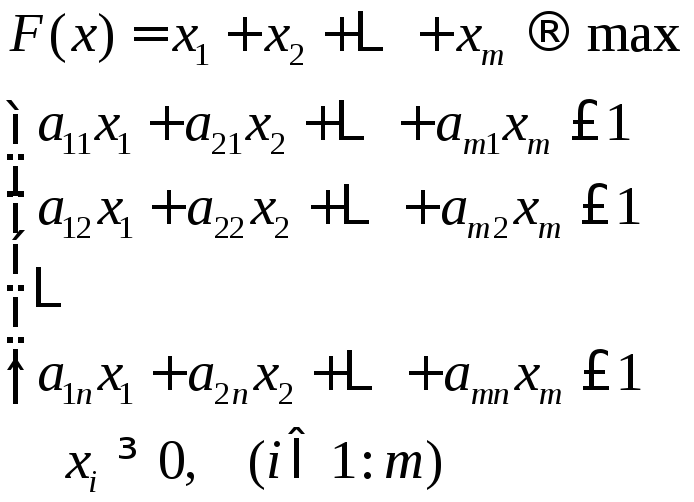
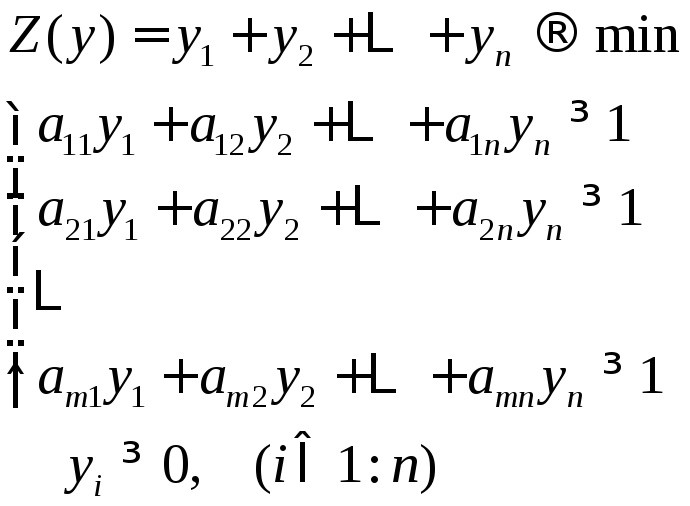

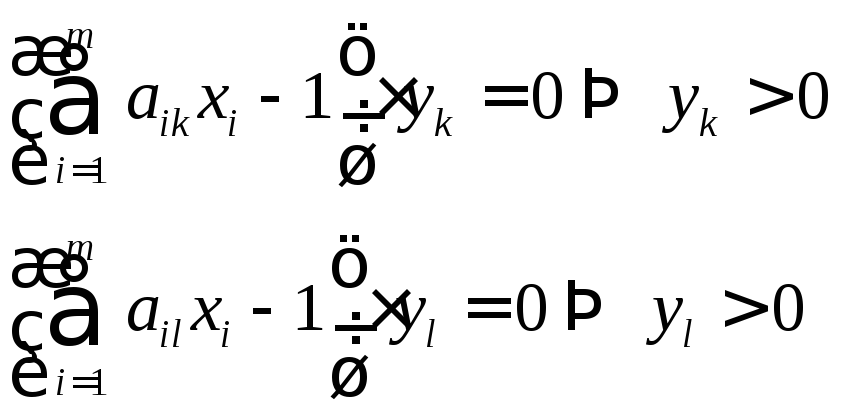
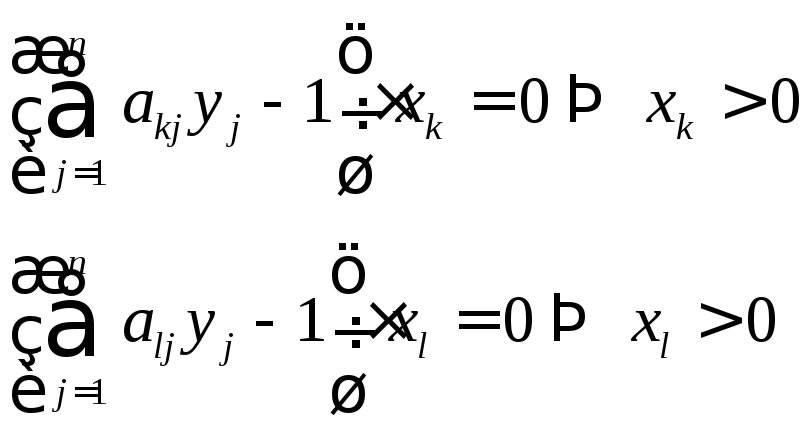

 гра
гра

 гра
гра