1.7. Відповідність, відображення і функції

Відповідність - відповідністю між множинами А и В називається підмножина G  А х В. Відповідність G називається функціональною або однозначною, якщо образом будь-якого елемента множини G1 є єдиний елемент множини G2, причому G1, G2  G.

Приклад. Англійсько – російський словник встановлює відповідність між множиною англійських і російських слів. Ця відповідність не є функціональною.

Функцією називається функціональна відповідність. Якщо функція f встановлює відповідність між множинами А и В, то кажуть, що функція f має тип АВ (позначення f : АВ). Цілком визначена функція f : АВ називається відображенням А в В. Образ А при відображенні f позначається f(A).

Якщо f(A) складається з єдиного елемента, те f називається функцією - константой.

Відображення типу АА називається перетворенням множини А.

Важливим поняттям при побудові математичних моделей дискретної математики є поняття відношення між елементами двох множин. Якщо для кожного елемента x  X можна сказати, що елемент x знаходиться або не знаходиться в даному відношенні  з елементом y  Y, то кажуть, що між елементами множини X і Y задане відношення , і пишуть x  y, у тому випадку, коли x знаходиться у відношенні  з елементом y. Наприклад, між множиною Х студентів даного курсу і множиною Y усіх навчальних предметів по даній спеціальності існує відношення  таке, що х  y означає "студент х здав екзамен з предмету y". Між елементами множин Х и Y може існувати багато різноманітних змістовних відношень, якщо Х и Y - змістовні множини. Наприклад, такими відношеннями є усілякі функціональні відношення, або відображення.

Відношення  між елементами множин X і Y називають відображенням множини Х в множину Y, якщо кожний елемент х  Х обов'язково знаходитися у відношенні з деяким елементом y  Y, причому цей елемент y  Y - єдиний для даного елемента х  Х. Відображення множини Х в множину Y позначають через  (або іншою підхожою буквою) і пишуть : Х  Y, при цьому замість х  y для х  Х и y  Y часто пишуть y = (х) і кажуть що y є представлення елемента х при відображенні. На рисунку відображення  : Х  Y зручно наводити у вигляді двочасткового графа. Розглянемо приклад (рис.1.9).

х₁ х₂ х₃ х₄

X

Y

у₁ у₂ у₃ у₄

Рис.1.9. Двочастковий граф.

Тут точки верхнього ряду зображують елементи множини Х, нижнього ряду - множини Y, і якщо має місце y = (x), то з точки х виходить стрілка, що заходить або входить у точку y. Таку форму представлення називають двочастковим графом відображення : X  Y, причому точки цього рисунка іменують вершинами графа, а стрілки - дугами графа і кажуть, що відображення  є :

а). Інєктивним, якщо в кожну вершину y  Y заходить або входить не більш однієї дуги ;

б). Сюрєктивним, якщо в кожну вершину y  Y входить не менше однієї дуги ;

в). Бієктивним, або бієкцією, якщо  інєктивно і сюрєктивно одночасно.

Для будь-якого відображення  : X  Y і будь-якого не порожньої підмножини А  Х множина образів всіх елементів х  А при відображенні  називають образом множини А и позначають (А),так що (А) = y Y : y = (x) для деякого х  А.

Для спільності і стрункості суджень приймається () = . Якщо (Х) = Y, то, очевидно,  є сюрєктивним відображенням.

У додатках часто використовується відображення : Х  R⁺, при цьому (х) виступає в ролі ціни, або ваги, або довжини, або пропускної спроможності елемента х  Х.

Очевидно, завдання бієкції : X  Y рівнозначно встановленню взаємно однозначної відповідності між елементами множин Х и Y.

Відображення : ХY і Y1: ХY називаються рівними, якщо з х  y випливає x ₁ y і навпаки, тобто якщо ці відображення можна зобразити двочастковим графом відображення.

Нехай Х и Y - кінцеві непорожні множини, причому |X| = m, |Y| = n. Тоді кількість усіх відображень : X  Y дорівнює nm. Дійсно, щоб одержати довільне відображення : X  Y, треба побудувати двочастковий граф цього відображення, для чого вибрати для кожної вершини x  X одну і тільки одну дугу серед n дуг (n = |Y| ), що можуть виходити з вершини х і заходити у вершини y  Y, причому для різних вершин х, х₁ Х зазначений вибір дуг робиться незалежно. Тому кількість усіх таких виборів, а виходить, і всіх двочасткових графів відображень буде n*n*... *n, де кількість співмножників дорівнює m = |X|, так що утворюється шукана кількість nm.

Множина усіх відображень :XY іноді позначають як Y^х, тому що для кінцевих X і Y тоді одержують формулу |Y^х| = |Y^х|. Але ніщо не заважає розглядати останню формулу для нескінченних X і Y і вважати цю формулу правилом зведення в кардинальний ступінь |X| кардинального числа |Y|.

Наприклад, с = 2^а . Далі, суму |X| + |Y| довільних кардинальних чисел визначають як потужність |X + Y| множини X + Y, створеної з усіх вершин х  Х и y  Y двочасткового графа довільного відображення : X  Y, а добуток |X| * |Y| визначають як потужність |X * Y| множини X * Y, створеного з всіляких упорядкованих пар (x, y), де x  X, y  Y. Таким чином, із дуг двочасткового графа, у якому з кожної вершини x  X виходять дуги в кожну вершину y Y. Таке визначення суми і добутки кардинальних чисел узгоджується зі звичним змістом m + n і m * n для кінцевих множин X і Y при m = =|X|, n = |Y|.

Перетворення. Відображення :XX називають перетворенням множини Х и на рисунку зображують у вигляді орграфа (орієнтованого графа) перетворення, вершинами якого є елементи x  X, а дугами - пари (х₁, х₂) такі, що х₁  х₂, тобто х₂ = (х₁). Перетворення : X  X можна зображати дворядковим записом, вміщуючі в першому рядку цього запису елементи x  X, а в другий - під ними їх представлення (х). Наприклад, для Х = 1,2,… ,7 одне з перетворень зобразимо дворядковим записом і орграфом (рис1.10):

1 2 3 4 5 6 7 1 3

= 2 4 5 6

3 7 2 5 4 6 1 7

Рис.1.10. Приклад перетворення

Очевидно, що це перетворення бієктивне, причому (А) = А для множин А=, А = 1,2,3,7 А = 4,5 ,А = 6, і тільки для них.

Бієктивні перетворення називають підстановками. Очевидно орграф підстановки  кінцевої множини розпадається на частині, однозначно обумовлені підмножинами А такими, що А = (А). Такі частини (вершини разом із дугами ) прийнято називати циклами підстановки . Максимальна кількість циклів має тотожні підстановкі , тобто такі, що х = (х) виконується для довільного х  Х. Підстановки, що мають один цикл, називаються одноцикловими. Одноциклові підстановки слугують, наприклад, моделями для опису обходу одною людиною n різноманітних пунктів (почавши рух у вихідному пункті, людина обходить всі інші по одному разу і повертається у вихідний пункт). Зауважимо, що кількість усіх підстановок n -елементної множини Х дорівнює n! = n * (n-1)*... *2*1, тому що елементу x1  X можна поставити у відповідність довільний із n елементів множини Х, але елементу х₂ при х₂  х₁, можна поставити у відповідність по підстановці  будь-який елемент із що залишилися n-1 елементів, що не є образом елемента х₁ і т.д.

У зв'язку зі сказаним вище зручно позначити через Х! множина всіх бієктивних перетворень множини Х, тому що тоді | X! | = | X |! для кінцевих множин Х.

Рекомендується пам'ятати, що 10! = 3628800, а 0! = 1 (за угодою).

Зрозуміло, кількість всіх одноциклових підстановок n - елементної множини дорівнює (n-1)! .

Приклад 1. Кожне натуральне число можна розкласти на добуток простих чисел. Якщо розташувати прості дільники у певному порядку наприклад, не зменьшення, то одержимим функцию

G(42)=(2, 3, 7); G(23)=23;

G(100)=(2, 2, 5, 5) і т.д.

Приклад 2. Кожній людині відповідає множина його знайомих.

G(Іванов)=(Сидоров, Миколаїв, ... ,Семенов)

Засоби завдання функцій.

Найбільше простий засіб завдання функцій - це таблиця, тобто список пар (x, f(x)). Проте в такий спосіб можуть задаватися тільки функції, визначені на кінцевій множині. Таблиці функцій, визначених на нескінченних множинах (наприклад, тригонометричних) задають ці функції тільки в кінцевому числі точок.

Іншим засобом завдання функцій є формула, що описує функцію, як суперпозицію інших (вихідних) функцій. Для завдання функції можуть використовуватися також графіки.

Ще два засоби завдання функцій:

а) рекурсивна процедура;

б)  x, якщо xM

f(x) =  (1.3)

 0, якщо xM

Всі наведені положення використовуються в інших розділах дискретної математики

Задачі.

1. Знайдіть множини АУ, АУ, А\У, У\А, якщо:

а) А={3, 5, 6, 7, 9}, У={4, 6, 7, 8};

б) А={3, 5, 6, 7, 9}, У={2, 4, 8};

в) А={2, 3, 4, 5, 6}, У={3, 4, 5};

г) А=Z, У=N; д) А=R, У=Q,; е) А=Z, У =Q;

ж) А=xxR, -1x5,У=xxR, -3x2;

з) А=xxR, -1x3, У=xxR,3x5;

и) А-множина всіх прямокутників, В- множина всіх ромбів.

2. Знайдіть множини А і У якщо:

а) А\У=a, b,У\А=c, d,АУ=x, y, z;

б) АУ=a, b, c, d, e, f,АУ=c, d, А\У=a, e, f ;

в) АУ=a, b, c, d, АУ=, А\У=a.

3. Нехай А - множина рішень рівнянь f(x)=0, У - множина рішень рівняння g(x)=0. Висловите через А и В множина рішень:

а) рівняння f(x)g(x)=0;

б) рівняння f(x)g(x)=0;

в) системи рівнянь f(x)=0;

g(x)=0.

4. Висловте множину дійсних коренів рівняння f(x)=0 через множини А=xf(x)0 і У=xf(x)<0.

5. Знайдіть такі множини:

а) А; б) А; в) АА; г)АА;

д) А\А; е) А\; ж) /А.

6. Дано множини А и В , причому АВ. Знайдіть:

а) АУ; б) АУ; в)А\В.

7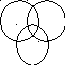. На діаграмі Эйлера-Венна зображені множини А, В, С (рис1.11). Зазначте (заштрихуйте) на цій

діаграмі множини: А В

а) АВ(ВС); б) А(ВС); С

в) (А\В)С;

г) (А\В)(В\С). Рис.1.11. До задачі 7.

8. Доведіть,що для будь-яких множин А, В, С:

а) А(ВС)=(АВ)(АС);

б) А(ВС)=(АВ)(АС);

в) А\(ВС)=(А\В)(А\С).

9. Нехай А и В - підмножини множини М. Доведіть , що :

а) А В=А  В; б) А В= АВ.

10. Множина А складається з n элементов, а множина В - з m елементів (m>n). Яке найбільше і найменше число елементів можуть містити множини АВ, АВ, А\В, В\А?

11. Доведіть, що якщо А складається з n елементів, В- із m елементів,

АВ - із k елементів, то множина АВ складається з n+m-k елементів.

12. Кожний учень у класі вивчає англійську або французку мову. Англійську мову вивчають 25 чоловік, французьку-27, а обидві мови-18. Скільки учнів у класі ?

13. У класі 30 учнів. Кожний із них займається футболом, або хокеєм. Половина учнів класу займається хокеєм, а 5 учнів - і хокеєм і футболом. Скільки учнів у класі займається футболом ?