Лекции Хуторецкий

2

AT ― результат транспонирования матрицы A. det(A) ― определитель квадратной матрицы A.

A–1 ― обратная матрица для квадратной матрицы A.

f(x) → max при условии x X ― запись задачи оптимизации: найти хотя бы один эле-

мент x X такой, что f(x) ≥ f(x') для всех x'X. Здесь X ― произвольное, вообще говоря, мно-

жество допустимых решений. Предполагается, что функция f определена на X. Argmax{f(x) | x X} ― множество всех точек максимума функции f(x) на множестве X.

P* ― задача, двойственная для задачи линейного программирования P.

P(A, b, c) ― возмущенная задача линейного программирования.

A0, b0, c0 ― исходные значения параметров задачи P(A, b, c). x(A, b, c) ― оптимальное решение задачи P(A, b, c).

y(A, b, c) ― оптимальное решение двойственной задачи P*(A, b, c).

N(β) ― базисное множество для базиса β.

xб(β) базисная часть вектора x относительно базиса β. xн(β) ― небазисная часть вектора x относительно базиса β.

B(β) ― базисная матрица для базиса β.

B–1(β) ― обратная базисная матрица для базиса β.

x(β) ― базисное допустимое решение ЗЛП в канонической форме, порожденное допус-

тимым базисом β.

Uc ― область постоянства оптимального решения для ЗЛП в канонической форме.

Если с0j = cj для всех j s, то Uc(j) ― множество всех значений cs, при которых базис β,

допустимый и оптимальный в задаче P(A0, b0, c0), остается таковым в задаче P(A0, b0, c). Ub ― область постоянства двойственных оценок для ЗЛП в канонической форме.

Если bi0 = bi для всех i r, то Ub(r) ― множество всех значений br, при которых базис

β, допустимый и оптимальный в задаче P(A0, b0, c0), остается таковым в задаче P(A0, b, c0).

G = (I, (Xi | i I), (ui | i I)) статическая игра с полной информацией в нормальной форме;

I ― множество игроков, Xi ― множество всех стратегий игрока i, ui(x) ― функция выигры-

ша игрока i, определенная на множестве X = X1 X2 … Xm всех исходов игры.

X–i = X1 … Xi–1 Xi+1 … Xm.

x–i = (x1, …, xi–1, xi+1, …, xm) X–i для x = (x1, …, xm) X ― набор стратегий всех игроков, кроме игрока i.

x = (xi; x–i) ― исход статической игры, представленный в виде пары, состоящей из стра-

тегии xi игрока i и набора x–i стратегий всех других игроков.

Ri(x–i) ― отображение отклика игрока i, определенное на X–i.

4

GM ― смешанное расширение игры G.

μi = (pik | k 1, n(i) ) ― смешанная стратегия игрока i, имеющего n(i) чистых стратегий. eik ― вырожденная смешанная стратегия игрока i, соответствующая его чистой страте-

гии с номером k.

G = (X, Y, F(x, y))

G = (A, B) ― биматричная игра.

G = (A) ― матричная игра.

5

1. Введение в предмет (2 ч.)

1.1. Основные понятия

Менеджер (руководитель, управляющий, организатор, администратор), принимает ре-

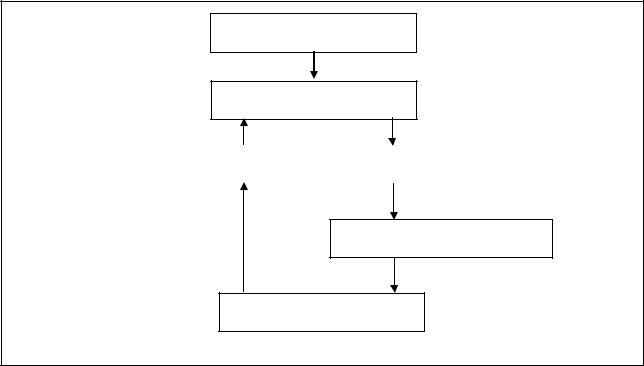
шения, осуществляет их и отвечает за результаты. Следовательно, он ― лицо, принимающее решения (ЛПР), или оперирующая сторона. Менеджер является элементом управляющей системы, которая в совокупности с объектом управления образует систему управления (см.

рис. 1).

Состояние внешней среды

Объект управления

Степень достижения цели

Управляющая система

Система управления

Рисунок 1. Структура системы управления

В каждый момент объект управления находится в некотором состоянии. Цель управле-

ния определяет множество желательных состояний объекта. Мы предполагаем, что управ-

ляющая система способна идентифицировать текущее состояние объекта управления. Если оно не принадлежит множеству желательных состояний, то ЛПР выбирает управляющее воз-

действие (управление), чтобы перевести объект в желательное состояние. Такое управление будем называть целесообразным. Выбор целесообразного управления есть решение менед-

жера. Результат управляющего воздействия и множество желательных состояний зависят от

состояния внешней среды.

1.2. Исследования в менеджменте и модели систем управления

Объектом исследования в менеджменте является система управления. Предмет иссле-

дования, как правило, ― взаимосвязь между состоянием внешней среды, управляющим воз-

6

если объект управления находится в состоянии s0. Для максимизируемой целевой функции

X*(a, s0) ={x X(a) | (a, x, s0) S*(a)} = {x X(a) | x'X(a) (F(a, x, s0) ≥ F(a, x', s0))}

Исследование состоит, как правило, из следующих этапов:

1.Анализ системы управления и выявление проблемы.

2.Содержательное описание (постановка) проблемы.

3.Построение отражающей проблему модели системы управления.

4.Анализ модели и выбор целесообразного (переводящего систему в желательное со-

стояние) управления.

5.Разработка и обоснование рекомендаций для ЛПР.

1.3. О содержании курса

Курс объединяет сведения из исследования операций (operations research, OR), науки о методах управления (management science, MS), теории принятия решений (decision theory),

системного анализа (system analysis). Все указанные дисциплины включают разделы, связан-

ные с математическими моделями систем управления. Приведенные ниже авторитетные мнения свидетельствуют о взаимосвязях между этими дисциплинами.

«Operations research и management science включают использование математического моделирования и статистических методов для анализа сложных бизнес-процессов и приня-

тия хороших решений».(1) Исследование операций ― это «применение … математических подходов к принятию деловых решений; другое название ― management science».(2) «В со-

временном словоупотреблении термины operations research, management science, system analysis можно считать почти синонимами».(3) «Математическими расчетами, облегчающими принятие целесообразных решений, занимается теория математических моделей и методов принятия оптимальных решений, или, другими словами, исследование операций».(4)

Мы будем изучать методы построения и анализа математических моделей систем управления. Такие модели формулируют на языке математики и анализируют средствами математики. В математической модели состояние внешней среды описывается набором не-

управляемых входных показателей, управляющее воздействие ― совокупностью переменных

модели (управляемых входных показателей), состояние объекта управления ― множеством

выходных показателей. Наша задача ― освоить базовые, широко применяемые и хорошо ис-

следованные классы моделей, соответствующие основным типам ситуаций выбора.

(1)Crowder H.P. The Science of Smart Decisions // OR/MS Today, 2000. V. 27. No. 3.

(2)Operations research // Imber J., Toffler B.-A. Dictionary of marketing terms. 4th edition. N.Y.: Hauppauge, 2008 (Barron's Educational Series).

(3)Lesso W.G. Operations research // McGraw-Hill Concise Encyclopedia of Science and Technology. New York: McGraw-Hill, 2002.

(4)Гимади Э.Х., Глебов Н.И. Математические модели и методы принятия решений. Новосибирск, НГУ,

2008.

8

Типы ситуаций выбора различаются степенью доступности для ЛПР в момент приня-

тия решения информации о состоянии внешней среды в период реализации этого решения.

Пусть A0 A ― множество состояний, в которых может находиться внешняя среда в период реализации решения.

Если A0 = {a0}, состояние внешней среды можно считать известным, то имеем ситуа-

цию выбора в условиях определенности (детерминированная ситуация).

Если множество A0 не одноэлементное и на нем задано распределение вероятностей

(например, одна из характеристик внешней среды является случайной величиной), то выбор происходит в условиях риска (стохастическая, или вероятностная, неопределенность).

Если множество A0 не одноэлементное, но распределение вероятностей на нем неиз-

вестно, то возникает ситуация природной (интервальной) неопределенности.

Выбор решения происходит в условиях субъективной (игровой) неопределенности, ес-

ли на состояние внешней среды влияют какие-то целеустремленные агенты (ЛПР, пресле-

дующие собственные цели).

Особого внимания требует формализация «смешанных» ситуаций, в которых доступ-

ность информации о некоторых характеристиках внешней среды соответствует различным типам неопределенности. В недетерминированной ситуации состояние объекта управления следует описывать так, чтобы функция реализации не зависела от неопределенных парамет-

ров внешней среды. Для этого обычно используют усреднение по случайным параметрам внешней среды (ожидаемый результат) и минимизацию полезного эффекта по неопределен-

ным параметрам (гарантированный результат).

1.4. Задачи математического программирования

Пусть S и A ― множества возможных состояний некоторого экономического объекта и его внешней среды соответственно.

Предположение 1. Объект управляем, то есть ЛПР может выбором решения влиять на поведение и состояние объекта.

Предположение 2. Известна функция реализации, s = (a, x, s0), сопоставляющая каж-

дой тройке (a, x, s0), где a A, x X(a) и s0 S, состояние, в которое переходит объект из ис-

ходного состояния s0, если в состоянии a внешней среды применить к нему управление x.

Предположение 3. ЛПР имеет цель, которая для каждого возможного состояния внеш-

ней среды a A указывает множество S*(a) желательных состояний объекта управления.

Предположение 4. Выбор решения происходит в условиях определенности, то есть со-

стояние a0 внешней среды в период реализации решения известно оперирующей стороне.

9

Фиксированные аргументы a0 и s0 можно исключить, поэтому положим X = X(a0),

Предположение 5. Известна оценочная функция, h(s), которая указывает, в какой сте-

пени достигается цель ЛПР, если объект находится в состоянии s.

Предположение 6. Функция h(s) возрастает по мере приближения к цели.

Тогда желательными являются те состояния, в которых оценочная функция достигает максимума. Целевая функция принимает вид f(x) = h( (x)), определена на X и указывает сте-

пень достижения цели в результате решения x.

При сделанных предположениях задача (1) является задачей оптимизации: найти оп-

Обозначение. Rn ― арифметическое пространство размерности n, множество всех век-

торов-столбцов вида x = (x1, …, xn)T, где xi R для всех i.

Предположение 7. Решения описаны как числовые векторы, то есть конечные наборы значений числовых показателей, управляемых входных параметров: x Rn.

При этом предположении задача (2) является задачей математического программиро-

Предположение 8. Множество допустимых решений X есть множество всех решений

конечной системы ограничений: уравнений и/или нестрогих неравенств.

Задача (3), дополненная предположением 8, становится задачей нелинейного програм-

мирования.

Обозначение. Для целых чисел m и n положим m, n = {m, …, n}, если m ≤ n, и m, n =

10