
1_konspekt
.docЛекция 1. Параллельное проектирование и его свойства. Изображение плоских фигур, многогранников и круглых тел при параллельном проектировании.
Литература: [1] § 26 – 29, [2] §1 – 3.
Пусть в пространстве дана некоторая
плоскость и вектор
![]() ,
который ей не параллелен.
,
который ей не параллелен.
О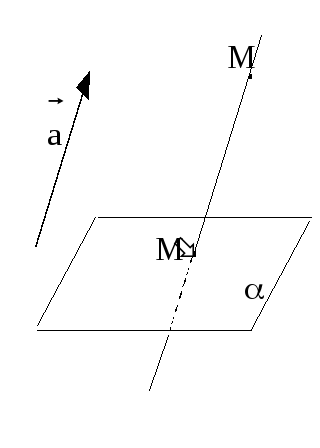 пределение
1. Под параллельной проекцией точки
М на плоскость
в направлении вектора
пределение
1. Под параллельной проекцией точки
М на плоскость
в направлении вектора
![]() понимается точка М,
полученная при пересечении плоскости
и прямой,
параллельной
понимается точка М,
полученная при пересечении плоскости
и прямой,
параллельной
![]() и проходящей через М.
и проходящей через М.
Ясно, что вместо вектора
![]() для определения параллельной проекции
точки на плоскость можно взять прямую,
не параллельную этой плоскости.
для определения параллельной проекции
точки на плоскость можно взять прямую,
не параллельную этой плоскости.
Е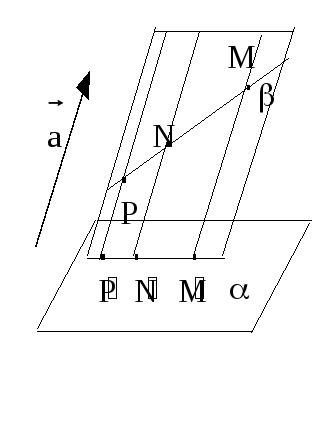 сли
в пространстве дана некоторая фигура,
то, проектируя каждую ее точку, мы получим
параллельную проекцию этой фигуры на
плоскость.
сли
в пространстве дана некоторая фигура,
то, проектируя каждую ее точку, мы получим
параллельную проекцию этой фигуры на
плоскость.
Будем предполагать в дальнейшем, что рассматриваемые в пространстве прямые, лучи и отрезки не параллельны направлению проектирования. При параллельном проектировании выполняются следующие свойства.
-
К
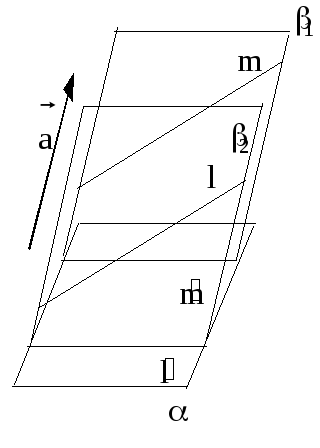 оллинеарные
точки отображаются в коллинеарные и
сохраняется их простое отношение.
оллинеарные
точки отображаются в коллинеарные и
сохраняется их простое отношение. -
Прямая проектируется в прямую, отрезок – в отрезок, луч – в луч.
-
Параллельные прямые отображаются либо в параллельные прямые, либо в одну прямую.
-
Сохраняется отношение длин отрезков, лежащих на одной прямой или на параллельных прямых.
Изображение плоских и пространственных фигур при параллельном проектировании
Пусть в пространстве дана некоторая плоскость , ее мы будем называть плоскостью изображения. Дано также некоторое направление проектирования на плоскость . Рассмотрим некоторую фигуру F в пространстве. Спроектируем ее на плоскость , получим фигуру F.
О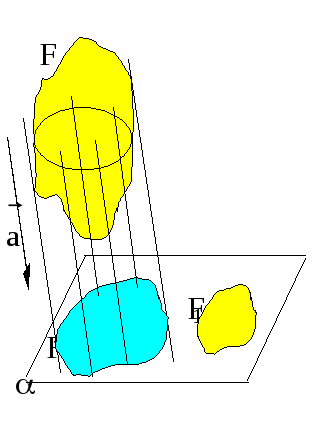 пределение.
Фигура F1
плоскости изображения, подобная F,
называется изображением фигуры F
при параллельном проектировании.
пределение.
Фигура F1
плоскости изображения, подобная F,
называется изображением фигуры F
при параллельном проектировании.
Введем понятие аффинного отображения одной плоскости на другую.
Взаимно однозначное отображение плоскости на плоскость называется аффинным, если при этом отображении коллинеарные точки отображаются в коллинеарные и сохраняется простое отношение точек.
Аффинное отображение плоскости на себя представляет собой аффинное преобразование этой плоскости, которое было изучено ранее. Аффинные отображения обладают теми же свойствами, что и аффинные преобразования плоскости: неколлинеарные точки отображаются в неколлинеарные точки, репер плоскости – в репер плоскости, прямая линия – а прямую линию, отрезок – в отрезок, луч – в луч. Справедливо также основное свойство аффинных отображений, которое доказывается практически дословно, как и основное свойство аффинных преобразований плоскости.
Основное свойство аффинных отображений. Пусть на плоскости дан аффинный репер R, а на плоскости - аффинный репер R. Тогда существует единственное аффинное отображение плоскости на плоскость , при котором репер R отображается в репер R.
Будем считать, что фигура F плоскости аффинно эквивалентна фигуре F плоскости , если существует аффинное отображение на , при котором образом F служит фигура F.
Из основного свойства аффинных отображений следует, что два треугольника, один из которых принадлежит плоскости , а другой плоскости , аффинно эквивалентны.
Два четырехугольника АВСD и ABCD, один из которых принадлежит плоскости , а другой плоскости , аффинно эквивалентны в том и только в том случае, когда (АС,О) = (AC,O), (BD,O) = (BD,O), где О и O' - соответственно точки пересечения их диагоналей AC и BD, АС и ВD.
Доказательства этого утверждения проводится дословно так же, как и в случае аффинных преобразований плоскости.
Справедлива следующая теорема.
Т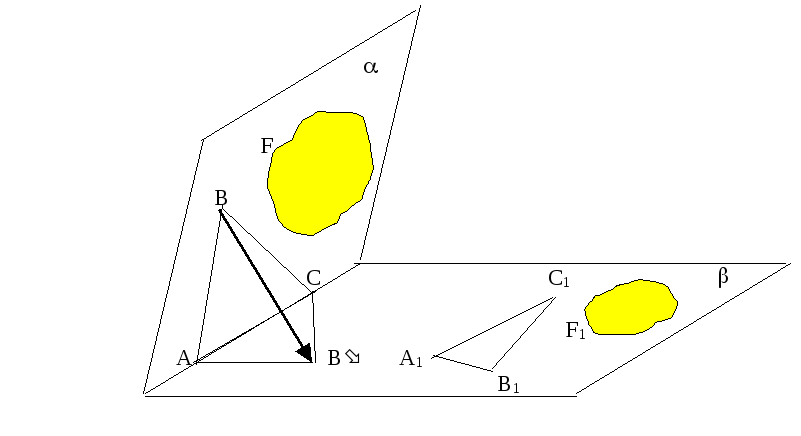 еорема.
Фигура F1
плоскости
служит изображением фигуры F
плоскости
в ом и только в том случае, когда они
аффинно эквивалентны.
еорема.
Фигура F1
плоскости
служит изображением фигуры F
плоскости
в ом и только в том случае, когда они
аффинно эквивалентны.
Треугольник изображается треугольником.
Четырехугольник – четырехугольником, точка пересечения диагоналей которого делит диагонали в том же отношении, что и у оригинала.
Поэтому прямоугольник, квадрат, ромб и параллелограмм изображаются параллелограммом.
Трапеция изображается трапецией, отношение оснований которой совпадает с отношением оснований оригинала.
Произвольный n – угольник
изображается n – угольником.
Рассмотрим пятиугольник ABCDE плоскости
, который изображается
пятиугольником A1B1C1D1E1
плоскости . Треугольник
ABC изображается
произвольным треугольником A1B1C1,
а точки D1E1 с троятся
следующими образом: точки пересечения
диагонали A1C1 с диагоналями
B1E1 и B1D1делит их
в том же отношении, что и у оригинала.
троятся
следующими образом: точки пересечения
диагонали A1C1 с диагоналями
B1E1 и B1D1делит их
в том же отношении, что и у оригинала.
Т ак
как эллипс и окружности аффинно
эквивалентны, то окружность изображается
эллипсом, а ее перпендикулярные диаметры
– сопряженными диаметрами эллипс, а
центр - центром.
ак
как эллипс и окружности аффинно
эквивалентны, то окружность изображается
эллипсом, а ее перпендикулярные диаметры
– сопряженными диаметрами эллипс, а
центр - центром.
Теорема Польке – Шварца. Вершины любого четырехугольника A1B1C1D1 плоскости , заданные в определенном порядке служат изображением аффинного репера, равного данному R(A,B,C,D).
Изображение пространственных фигур при параллельном проектировании.
Из теоремы Польке – Шварца следует, что изображением тетраэдра, равного данному, при параллельном проектировании может служить произвольный четырехугольник (в частности и не выпуклый).
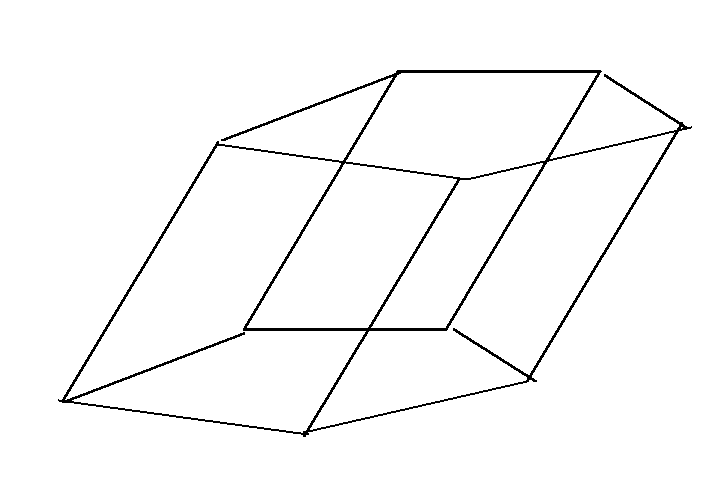
Изображением параллелепипеда, в том числе прямоугольного и куба, является фигура, состоящая из трех пар параллелепипедов, полученных друг из друга параллельным переносом.
П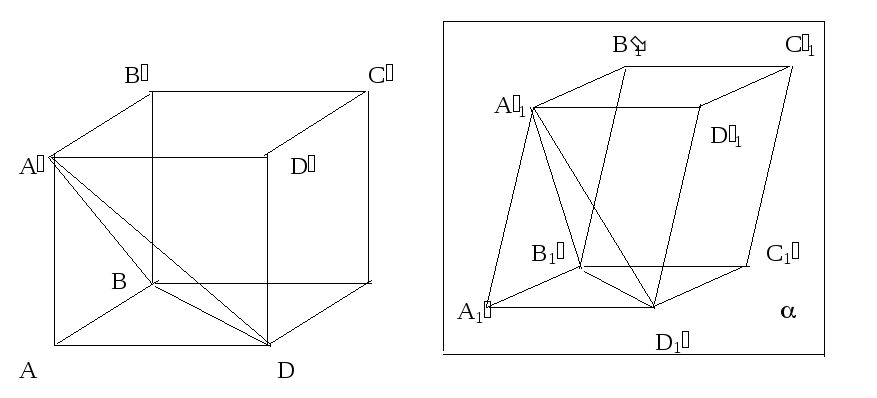
 ри
этом строится вначале изображение
тетраэдра ABDA.
И силу теоремы Польке – Шварца оно
представляет собой четырехугольник
A1B1D1A1
плоскости изображения .
Затем этот четырехугольник достраивается
до трех пар указанных параллелограммов.
ри
этом строится вначале изображение
тетраэдра ABDA.
И силу теоремы Польке – Шварца оно
представляет собой четырехугольник
A1B1D1A1
плоскости изображения .
Затем этот четырехугольник достраивается
до трех пар указанных параллелограммов.
Построение изображения призмы. Изображением n – угольной призмы служит фигура, состоящая из двух равных n – угольников – изображений оснований призмы, и n параллелограммов – изображений ее боковых граней. При этом построение изображений оснований подчиняется правилу построения изображения n – угольника.
Построение пирамиды. Основание n – угольной пирамиды изображается n - угольником, построение которого подчиняется правилу построения изображения n – угольника. Вершина пирамиды изображается точкой, а боковые грани – треугольниками.

При этом из теоремы Польке – Шварца следует, что в качестве изображения вершины пирамиды и трех вершин основания можно взять произвольный четырехугольник на плоскости.
Изображение цилиндра.
Д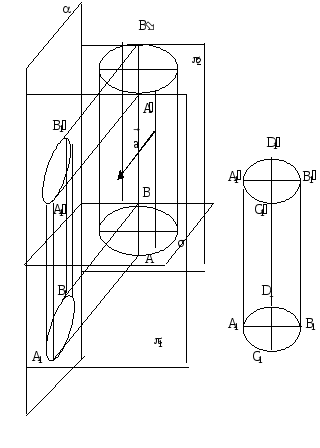 ан
прямой круговой цилиндр. Для наглядности
будем считать, что плоскость изображения
параллельна оси
цилиндра, а направление проектирования,
определенное вектором
ан
прямой круговой цилиндр. Для наглядности
будем считать, что плоскость изображения
параллельна оси
цилиндра, а направление проектирования,
определенное вектором
![]() не перпендикулярно .
Проведем плоскости 1
и 2,
перпендикулярные
и касающиеся цилиндра. Основания цилиндра
изобразятся эллипсами, а его образующие
АА и ВВ
- касательными к изображению оснований
(контурные образующие).
не перпендикулярно .
Проведем плоскости 1
и 2,
перпендикулярные
и касающиеся цилиндра. Основания цилиндра
изобразятся эллипсами, а его образующие
АА и ВВ
- касательными к изображению оснований
(контурные образующие).
 Изображение
конуса. Так же, как и в случае цилиндра,
выберем плоскость изображения параллельно
оси цилиндра, а вектор
Изображение
конуса. Так же, как и в случае цилиндра,
выберем плоскость изображения параллельно
оси цилиндра, а вектор
![]() ,
определяющий направление проектирования,
не перпендикулярно плоскости изображения.
Пусть - плоскость
основания конуса. Проведем через его
вершину S прямую, параллельную
вектору
,
определяющий направление проектирования,
не перпендикулярно плоскости изображения.
Пусть - плоскость
основания конуса. Проведем через его
вершину S прямую, параллельную
вектору
![]() .
Получим точку S
пересечения этой прямой и плоскости
основания. Тогда конус проектируется
в фигуру, полученную отрезками касательных
SA
и SB,
проведенных из точки S
к окружности основания, и самой
окружностью. Поэтому при проекции конуса
на плоскость мы
получим, что окружность основания
изображается эллипсом, изображение
вершины S принадлежит
прямой, содержащей ее меньшую ось, а
контурные образующие – отрезками
касательных, проведенных из изображения
вершины к изображению окружности
основания.
.
Получим точку S
пересечения этой прямой и плоскости
основания. Тогда конус проектируется
в фигуру, полученную отрезками касательных
SA
и SB,
проведенных из точки S
к окружности основания, и самой
окружностью. Поэтому при проекции конуса
на плоскость мы
получим, что окружность основания
изображается эллипсом, изображение
вершины S принадлежит
прямой, содержащей ее меньшую ось, а
контурные образующие – отрезками
касательных, проведенных из изображения
вершины к изображению окружности
основания.
Изображение сферы. При построении
изображения сферы используется
ортогональная проекция, иначе сфера
будет изображена эллипсом. Поэтому
изображением сферы служит окружность.
Для наглядности на изображении сферы
указывают окружность большого круга,
не перпендикулярную и не параллельную
плоскости изображения (экватор). Проведем
прямую, перпендикулярную плоскости
экватора. Изображения ее точек пересечения
со с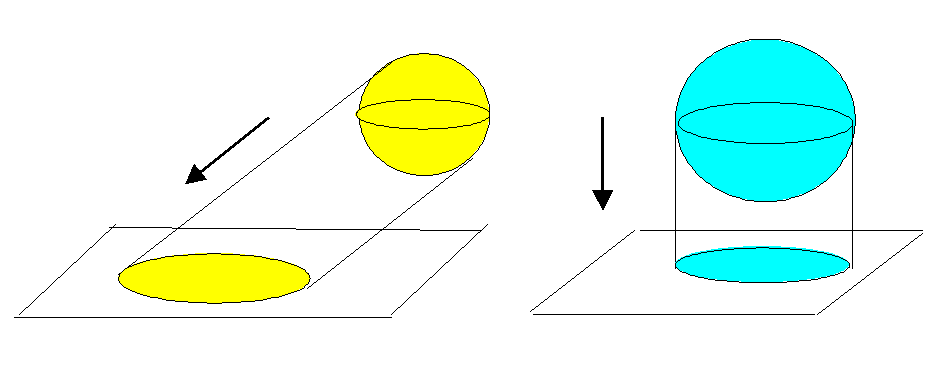

 ферой
называются полюсами. Полюсы сферы не
расположены на контурной окружности
сферы, иначе экватор сферы представляет
собой отрезок, а его плоскость –
параллельна плоскости изображения.
Укажем способ построения полюсов,
соответствующих данному экватору.
ферой
называются полюсами. Полюсы сферы не
расположены на контурной окружности
сферы, иначе экватор сферы представляет
собой отрезок, а его плоскость –
параллельна плоскости изображения.
Укажем способ построения полюсов,
соответствующих данному экватору.
Обозначим плоскость изображения через
, а плоскость экватора
через . АВ и CD
оси эллипса экватора на изображении.
Они принадлежат плоскости ,
Точки С и D
принадлежат большой окружности,
полученной при пересечении
и сферы. Эти точки проектируются в С и
D. Прямая SN
перпендикулярна плоскости ,
а сами эти точки служат пересечением
прямой и сферы. Таким образом:
![]() Величина угла между плоскостями
и равна .
Очевидно, этот угол совпадает по величине
с углом СОС
прямоугольного треугольника СОС,
а угол NON
прямоугольного треугольника NON
равен
Величина угла между плоскостями
и равна .
Очевидно, этот угол совпадает по величине
с углом СОС
прямоугольного треугольника СОС,
а угол NON
прямоугольного треугольника NON
равен
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() ,
а
,
а
![]() .
.
С другой стороны, если СК – касательная
к эллипсу экватора на изображении сферы,
то треугольник СОК прямоугольный,
![]() ,
и, как было доказано ранее,
,
и, как было доказано ранее,
![]() .
Поэтому
.
Поэтому
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() .
Таким образом,
.
Таким образом,
![]()
