
integraly_-_vse_(1) (1)
.pdf
|
|
dx |
Отв. _ |
2 |
|
|
1 |
|
|
C. |
|
|
12. |
I |
|
|
|
|
|
|
|
||||
|
. |
|
3 tg |
3x |
1 |
|
См. (8.6) |
|||||
sin 3x 1 |
|
|
||||||||||
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Часть 10. Тригонометрические подстановки
В части 4 был рассмотрен метод подстановки (замены переменной).
Для вычисления некоторых интегралов существуют стандартные подста-
новки, которые позволяют успешно и рационально вычислить эти интегра-
лы. Рассмотрим следующие, так называемые, тригонометрические подстановки.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подынтегральная |
Подстановка |
Новая подынтегральная |
||||||||||||||
функция |
функция |
|
||||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f x, |
|
|
|
|
x a sin t, x a cost |
f (asin t, a cost) (10.1) |
||||||||||
a2 x2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
a |
,(x |
a |
) |
f ( |
a |
|
, atgt) |
(10.2) |
|
f (x, |
|
x2 |
a2 ) |
|
||||||||||||
|
|
|
cos t |
|||||||||||||
|
|
|
|
|
|
|
cost |
sin t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
x a tgt, (x a ctgt) |
f (a tgt, |
|
a |
) |
(10.3) |
|||||
f (x, |
|
x2 |
a2 ) |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 42. Вычислим интеграл I 
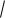 a2 x2 dx.
a2 x2 dx.
Решение. Для вычисления данного интеграла подойдет одна из три-
гонометрических подстановок, (см. (10.1))
Если x asint , то |
|
|
|
t arcsin |
x |
|
|
a2 x2 |
a cos t, |
dx a cos t, |
. Отсюда сле- |
||||
a |
|||||||
|
|
|
|
|
|
дует, что I 
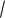 a2 x2 dx a cost a cost dt a2 cos2 t dt.
a2 x2 dx a cost a cost dt a2 cos2 t dt.
Новый интеграл в правой части не является табличным, но в части 8
интеграл такого вида был разобран (см. (8.3)). Преобразуем подынтегральную функцию необходимым образом и получим следующее.
51

|
2 |
|
1 |
1 |
cos 2t dt |
a2 |
dt |
a2 |
1 |
cos 2t d 2t |
a2 |
1 |
|
|
||
I a |
|
|
|
|
|
|
|
t |
|
sin 2t |
C. |
|||||
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
2 |
|
2 |
|
2 |
|
2 |
2 |
|
|
|
Для окончательного ответа в полученный интеграл необходимо под-
ставить t arcsin ax , но прежде, чем сделать это, преобразуем наш результат,
чтобы ответ выглядел интереснее.
|
1 |
|
1 |
|
1 |
|
1 |
|
|
|
|
|||||||||||||
Учтем, что |
sin 2x |
2sin t cost |
a sin t a cost |
x a2 |
x2 . И теперь |
|||||||||||||||||||
|
|
a2 |
|
|
|
|||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||
запишем окончательный ответ: |
I |
|
|
2 |
x |
2 |
a |
2 |
|
C. |
|
|
||||||||||||
|
x |
|
a |
|
|
|
arcsin |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|||
Замечание. Так с помощью тригонометрической подстановки была получена формула 19 таблицы 1 основных интегралов.
Пример 43. Вычислим интеграл I |
|
dx |
||
|
|
|
. |
|
x |
|
|
||
x2 9 3 |
||||
Решение. Проанализируем подынтегральную функцию, сравнивая ее со всеми случаями, рассмотренными в части 10.
Ответьте последовательно на следующие вопросы и выполните соот-
ветствующие преобразования.
1) Какая из тригонометрических подстановок подходит для вычисле-
ния данного интеграла? (см. таблицу 3)
(Подходит подстановка x cos3 t , (см.(10.2))
2) Прео6разуйте данный интеграл, |
подставив |
x |
3 |
|
|
, |
в подынте- |
|||||||||||
cost |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
3sin t |
dt |
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
||||
гральное выражение. |
( |
I |
|
|
cos t |
|
|
|
cos t |
dt. ) |
||||||||
|
|
|
|
|
|
|
2 |
|
||||||||||
|
|
|
|
3 |
|
|
3 |
|
27 |
|
|
sin |
|
t |
|
|||
|
|
|
|
|
3tgt |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
cost |
|
|
|
|
|
|
|
|
||||||
3) Имея уже достаточный опыт, вычислите получившийся после за- |
||||||||||||||||||
мены переменной интеграл. |
|
|
|
|
|
|
|
|
|
( |
|
1 |
ctgt t C ) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|||
52
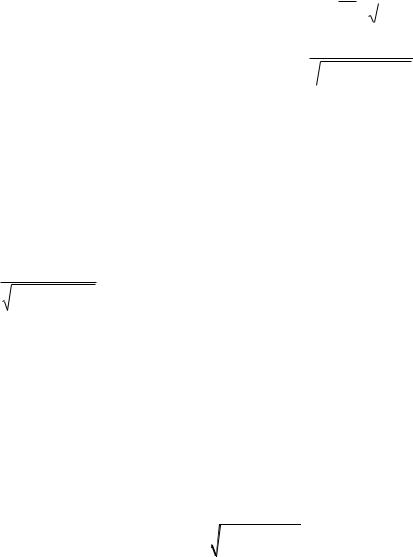
4) Перейдите к исходной переменной и выпишите окончательный
1
ответ. ( I
27
|
|
3 |
3 |
|
|
|||
|
|
|
|
|
arccos |
|
|
C. ) |
|
|
|
|
|
|
|||
|
x |
2 |
9 |
|
|
x |
|
|
|
|
|
|
|
|
|||
Пример 44. Вычислим интеграл I dx .
 x2 6x 10 5
x2 6x 10 5
Решение. Проанализируем подынтегральную функцию и выясним,
чем она характерна, какой метод вычисления интеграла следует выбрать. 1) Подынтегральная функция содержит квадратный трехчлен, поэто-
му, прежде всего следует в квадратном трехчлене выделить полный квад-
рат. (См. (6.1)). Выделив полный квадрат, получим интеграл
I |
dx |
, который пока не является табличным и не похож ни на |
x 3 2 1 5. |
один табличный интеграл.
2) Необходимо избавиться от иррациональности, что позволит сде-
лать замена переменной. Подынтегральная функция подобна функциям,
рассмотренным в части 10. Воспользуемся одной из тригонометрических подстановок. (См. таблицу 3).
Выбираем подстановку x 3 tgt, тогда
|
dt |
|
|
|
|
|
|
1 |
|
dx d x 3 dtgt |
|
, |
x 3 |
2 |
1 |
||||
|
|
|
|
|
|||||
cos |
2 |
|
|
cos t. |
|||||
|
|
t |
|
|
|
|
|||
Теперь относительно новой переменной интеграл будет выглядеть следующим образом.
I cos3 t dt .
3).Интегрирование нечетной степени тригонометрической функции было рассмотрено в части 8. (См. (8.2)).
Преобразуем должным образом подынтегральную функцию и вы-
числим получившийся интеграл.
53
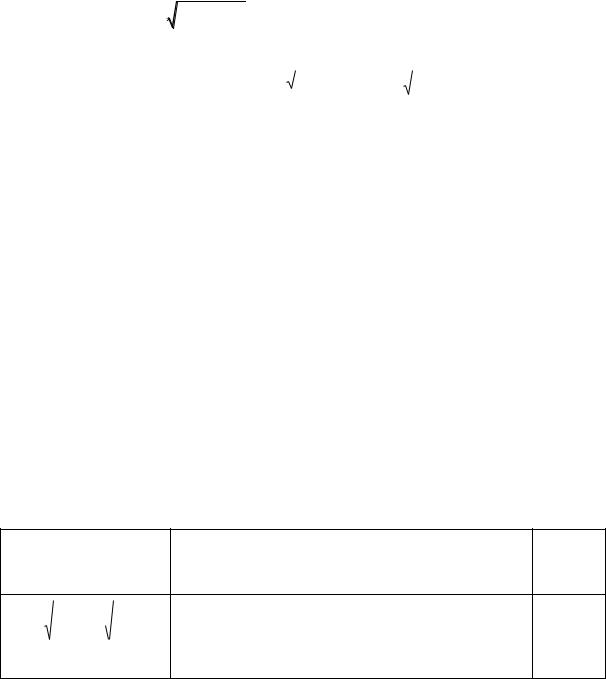
I cos2 t cos tdt cos2 td sin t 1 sin2 t d sin t d sin t sin2 td sin t |
|
||||||||||||||||||
sin t |
1 |
sin3 t C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы |
|
дать |
|
окончательный |
|
ответ, |
заметим, |
что |
|||||||||||
sin t tgt cos t x 3 |
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x 3 2 1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
x 3 |
1 |
|
|
|
x 3 3 |
|
||||
И теперь получаем ответ: I |
|
|
|
|
|
|
|
|
|
C. |
|
||||||||
|
|
|
3 |
|
|
|
|
||||||||||||
x2 6x 10 |
x2 6x 10 3 |
|
|||||||||||||||||
Замечание. В рассмотренном примере было применено несколько методов интегрирования, а именно, выделение полного квадрата, тригоно-
метрическая подстановка, интегрирование нечетной степени тригономет-
рической функции, подведение под знак дифференциала. Последователь-
ная постановка вопросов и ответы на них привели к успешному решению задачи.
Часть 11.Интегрирование некоторых иррациональных
функций
Рассмотрим еще несколько стандартных подстановок, применяю-
щихся при интегрировании некоторых иррациональных функций.
Таблица 4.
Подынтегральная
Подстановка
функция
|
|
|
|
|
|
|
|
|
|
ax b |
|
|
f (x, m |
ax b |
|
, n |
ax b |
) |
tr , где r |
- наименьшее общее крат- |
|||||
|
|
cx d |
||||||||||
cx d |
|
cx d |
|
|
(11.1) |
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
ное чисел m и n . |
|
||
54

|
|
Подстановки Чебышева |
|
|
|
|
||||
|
|
1) Если |
|
p целое число, то x ts , |
где s - |
|
||||
f (x) xm a bxn p |
|
наименьший общий знаменатель чисел m |
|
|||||||
, |
и n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где m, n, p - |
|
2) Если |
|
m 1 |
целое число, то |
a |
bxn ts , |
(11.2) |
||
|
|
|
||||||||
|
|
|
|
|
||||||
рациональные |
|
|
|
n |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
числа |
|
где s знаменатель дроби p . |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3) Если |
m 1 |
p целое число, |
то |
a |
b ts , |
|
||
|
|
|
|
xn |
||||||
|
|
|
|
n |
|
|
|
|||
|
|
где s знаменатель дроби p . |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Замечание. Не любой интеграл от иррациональных функций может быть выражен через элементарные функции. То есть не любая иррацио-
нальная функция имеет элементарную первообразную. В частности, для интеграла вида I xm a bxn p dx имеет место следующая теорема Чебыше-
ва. |
|
|
|
||
Интеграл |
I xm a bxn p dx может быть выражен в элементарных |
||||
функциях только в трех случаях: |
|||||
если p целое число, |
|||||
если |
m 1 |
целое число, |
|||
n |
|
||||
|
|
|
|||
если |
|
m 1 |
p целое число. |
||
|
n |
|
|||
|
|
|
|||
Если p целое положительное число, то выражение преобразуется по формуле бинома Ньютона, если p целое отрицательное или дробное число,
то возможные подстановки даны в таблице 4.
|
|
|
|
|
|
|
Пример 45. Вычислим интеграл I |
1 4 x |
|
dx. |
|||
|
|
|
|
|
||
|
x |
|||||
|
|
|
|
|||
55

1
Решение. Подынтегральная функция имеет вид f (x) x 2 1
1
1 2
x 4 .
Проверим, выполняется ли для нее одно из условий Чебышева. (См.
(11.2)).
|
|
Имеем m |
1 |
, |
n |
1 |
|
, p |
1 |
. |
Так как |
p |
целое положительное число, |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
вычисляем |
|
|
m 1 |
|
|
2 . Результат есть целое число. Для вычисления данного |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s 2 |
|
|
|
|||||||||||||||||||||||||||
интеграла подойдет подстановка |
|
1 x 4 t 2 , где |
|
|
знаменатель |
дроби |
|||||||||||||||||||||||||||||||||||||||||||||||||
p |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Из подстановки следует, |
|
что x |
|
t2 1 |
4 , |
dx 8 |
|
t2 1 3 tdt . И |
после |
||||||||||||||||||||||||||||||||||||||||||||
преобразования данный интеграл будет иметь следующий вид. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
I |
|
|
|
|
|
t |
|
|
|
|
|
|
8 t |
2 |
1 |
3 |
tdt 8 t |
2 |
t |
2 |
1 dt 8 |
1 5 |
1 3 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
t |
|
C. |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
3 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
t |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Возвращаясь к исходной переменной, получаем окончательный от- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
вет: I |
8 |
|
|
1 4 |
|
|
|
5 |
1 4 |
|
3 |
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Пример 46. Вычислим интеграл I |
|
|
|
|
|
dx |
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
4 3x2 3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Решение. Подынтегральную функцию можно представить в |
виде |
||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
4 |
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3x |
|
2 . Проверим, |
выполняется ли для нее одно из условий Че- |
||||||||||||||||||||||||||||||||||||||||||||||||||||
f (x) x |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
бышева. (См. (11.2)). Здесь m 0, |
n 2, |
p |
3 |
. Видим, |
что |
m 1 |
|
1 |
|
не яв- |
||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
n |
2 |
|
|
|||
ляется целым числом, а |
m 1 |
p 1 целое число. Поэтому данный инте- |
||||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
грал можно вычислить |
с |
|
помощью |
подстановки |
a |
b t s , |
то |
есть |
||||||||||||||
|
xn |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
4 |
3 t 2 . Отсюда следует, |
что |
x |
2 |
|
, dx |
|
2t |
|
|
dt . И после под- |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x2 |
|
|
|
|
t2 3 |
t2 3 3 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56 |

становки |
и |
|
преобразования данный |
интеграл |
принимает вид |
||||||||
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
I |
|
|
|
dt |
|
|
C . |
|
|
|
|
|
|
4t |
2 |
4t |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из выбранной подстановки следует, |
что |
t |
|
4 3x2 |
|
. Подставляя это |
||||||
|
|
x |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в полученный результат интегрирования, получаем окончательный ответ:
I |
|
|
x |
|
C. |
|
|
|
|
||
|
|
|
|
||
|
3x2 |
||||
4 4 |
|
|
|||
|
Пример 47. Вычислим интеграл I |
|
|
x3dx |
|
. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 x3 |
|
|
|
|
|
||||
|
Решение. |
|
Подынтегральную функцию можно |
представить в ви- |
||||||||||||||||
|
3 |
1 |
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
де f (x) x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Проверим, выполняется ли для нее одно из условий Чебышева. (См. |
|||||||||||||||||||
(11.2)). Имеем m 3, n 3, p |
1 |
. Видим, что p |
не является целым чис- |
|||||||||||||||||
|
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
лом, |
m 1 |
|
4 |
тоже не является целым числом и |
m 1 |
p |
5 |
не целое чис- |
||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
n |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
n |
6 |
|
|||
ло. Условия теоремы Чебышева не выполняются, а следовательно, данный интеграл нельзя выразить в элементарных функциях, то есть не существу-
ет такой элементарной функции, чья производная равна подынтегральной
|
f (x) |
|
x3 |
|||
функции |
|
|
|
|
. |
|
|
|
|
|
|||
|
|
|
||||
|
|
1 |
x3 |
|||
Ответ: данный интеграл является не берущимся.
Задачи для самостоятельной работы
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||
1. |
I |
|
|
|
|
|
dx . |
Отв. |
|
|
|
|
|
|
|
|
|
arcsin |
|
|
|
C. |
|
|
|
|
|
См.(10.1) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
9 x2 3 |
|
|
|
|
9 x2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
2. |
I |
|
|
|
|
x3 |
|
|
|
|
|
dx. |
Отв. |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
16 |
|
|
|
|
C. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
См.(10.2) и (8.5) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 16 3 |
|
|
||||||||||||||||||||
|
x2 16 5 |
|
|
|
x2 16 |
|
|
3 |
|
|
||||||||||||||||||||||||||||||||||
3. |
I |
|
|
|
|
|
dx |
|
|
|
|
|
. |
Отв. |
|
1 |
|
|
|
1 |
|
|
|
|
x |
|
|
|
|
1 |
|
C. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
ln |
tg |
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
|
См.(10.3) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
x2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
x |
|
4 |
|
|
8 |
|
|
|
2 |
|
|
|
|
2 |
|
|
4 x2 4 |
|
|
|||||||||||||||||||||
57
Список литературы
1. Зарубин B.C., Иванова Е.Е., Кувыркин Г.Н. Интегральное исчис-
ление функций одного переменного: Учеб. для вузов. /Под ред.
B.C.Зарубина, А.П.Крищенко. – М: Изд-во МГТУ им. Н.Э. Баумана, 2006.
–528 с. (Сер. Математика в техническом университете, вып. VI).
2.Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Интеграл-Пресс, 2006. – 416 с.
3.Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 2. – М.: Интеграл-Пресс, 2006. – 544 с.
4.Бугров Я.С., Никольский С.М. Высшая математика. Т. 2. Диффе-
ренциальное и интегральное исчисление. – М.: Дрофа, 2003. – 512 с.
5. Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб. пособие для втузов. /Под ред.
А.В.Ефимова, Б.П.Демидовича. – М.: Наука, 1993. – 478 с.
6. Сборник задач по математике для втузов. Ч. 2. Специальные раз-
делы математического анализа: Учеб. пособие для втузов. /Под ред.
А.В.Ефимова и Б.П.Демидовича. – М.: Наука, 1986. – 368 с.
7.Задачи и упражнения по математическому анализу для втузов. /Под ред. Б.П.Демидовича. – М.: Интеграл-Пресс, 1997. – 416 с.
8.Вся высшая математика: Учебник для втузов: В 6 т. /Краснов М.Л.,
Киселев А.И., Макаренко и др. – Т. 2. – М.: Эдиториал УРСС, 2000. – 184
с.
9. Вся высшая математика: Учебник для втузов: В 6 т. /Краснов М.Л.,
Киселев А.И., Соболев С.К. и др. – Т. 3. – М.: Эдиториал УРСС, 2001. – 237 с.
10. Добрица Б.Т., Роткова О.В., Шахов Е.М. Неопределенный инте-
грал. – М.: МГТУ, 1988.
58
Оглавление |
|
Введение........................................................................................................................ |
1 |
Часть 1. Основные сведения....................................................................................... |
2 |
Основные свойства неопределенных интегралов ..................................................... |
2 |
Таблица основных определенных интегралов для функции f(u)............................... |
|
Таблица 1....................................................................................................................... |
3 |
Часть 2. Тождественное преобразование подынтегральной функции................... |
4 |
Задачи для самостоятельной работы .......................................................................... |
6 |
Часть 3. Подведение под знак дифференциала ........................................................ |
7 |
Задачи для самостоятельной работы ........................................................................ |
13 |
Часть 4. Интегрирование по частям ........................................................................ |
14 |
Задачи для самостоятельной работы ........................................................................ |
20 |
Часть 5. Метод подстановки (замена переменной) ................................................ |
21 |
Задачи для самостоятельной работы ........................................................................ |
23 |
Часть 6. Интегрирование некоторых функций, содержащих квадратный |
|
трехчлен....................................................................................................................... |
24 |
Задачи для самостоятельной работы ........................................................................ |
29 |
Часть 7. Интегрирование рациональных дробей.................................................... |
30 |
Таблица 2..................................................................................................................... |
30 |
План разложения рациональной правильной несократимой дроби |
на сумму |
элементарных дробей................................................................................................. |
31 |
Метод Остроградского (выделение рациональной части интеграла) ................... |
38 |
Задачи для самостоятельной работы ........................................................................ |
40 |
Часть 8. Интегрирование тригонометрических функций...................................... |
40 |
Часть 9. Интегрирование гиперболических функций............................................ |
49 |
Задачи для самостоятельной работы.................................................................... |
50 |
Часть 10. Тригонометрические подстановки...................................................... |
51 |
Таблица 3..................................................................................................................... |
51 |
Часть 11.Интегрирование некоторых иррациональных функций ........................ |
54 |
Таблица 4..................................................................................................................... |
54 |
Задачи для самостоятельной работы ........................................................................ |
57 |
Список литературы..................................................................................................... |
58 |
|
59 |
