Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4614 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Московский государственный технический университет им. H.Э.Баумана
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

integraly_-_vse_(1) (1)

.pdf
Скачиваний:
13
Добавлен:
23.03.2016
Размер:
1.06 Mб
Скачать
☆

ментально. Однако этот интеграл можно представить как сумму двух инте-

гралов:

x 2

dx

 

 

x

 

dx

 

 

2

 

 

dx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

2

 

 

 

2

 

 

x

 

1

 

x

 

1

 

x

 

1

Из этих интегралов второй интеграл, как мы видим, является таблич-

ным при u x (см. таблица 1, формула 16), в первом же интеграле можно

1

подвести под знак дифференциала и x , и . Рассмотрим оба вариан-

x 2 1

та подведения под дифференциал.

 

 

 

 

1

 

xdx

1

 

 

x 2

 

 

1

 

 

dx 2

а)

 

 

 

 

 

 

 

 

 

d

 

 

 

 

 

 

 

, (см. (3.2));

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 2 1

 

 

 

x 2 1 2

 

 

2

 

x 2 1

б) x

 

dx

 

 

xd ln(x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 2 1) .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 2 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Полученный в пункте б) интеграл не похож ни на один из интегралов таблицы 1.

 

 

 

 

см.(3.1)

 

 

 

 

 

 

 

dx 2

a 1, b 1

d (x 2 1)

 

Полученный в пункте а) интеграл

 

 

 

 

 

 

 

похож на

 

 

 

 

 

 

x 2 1

x 2 1

 

 

u

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

du

при u x 2

1, который является табличным. См. таблицу 1 форм. 1

 

 

 

 

 

 

при u x 2 1, n

1

 

 

 

u 1/ 2du

u1/ 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

:

 

C 2

 

u C .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

1 / 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Окончательно получаем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 2

 

dx

 

 

 

x

 

 

dx 2

 

 

dx

 

 

 

1

 

 

 

 

dx 2

2

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 2 1

 

 

 

 

x 2 1

 

x 2 1

 

 

 

x 2 1

 

 

x 2 1

 

 

 

 

 

 

1

(x 2 1) 1/ 2d (x 2 1) 2

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x 2

1 2ln(x

x 2 1) C .

 

 

 

2

 

 

 

 

 

 

 

 

 

 

x 2 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: I

x 2 1 2ln(x x 2 1) C .

 

 

 

 

 

 

 

 

 

 

 

11

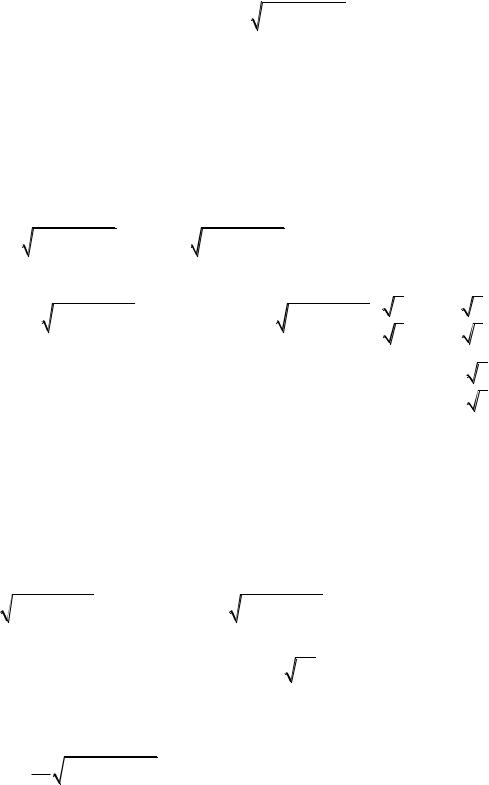
Пример 9. Вычислим интеграл

I

x 3 ln(2x 2 3)

dx .

 

 

2x

2

3

 

 

 

 

 

 

 

 

 

 

 

Решение. Данный интеграл не является табличным. Подынтеграль-

ная функция имеет два множителя

f1(x ) x

и

f2

(x )

1

 

, которые

 

 

2x 2

 

 

 

 

 

 

 

 

3

можно проинтегрировать и подвести под знак дифференциала. После под-

ведения под знак дифференциала интеграл будет иметь следующий вид:

 

1

 

3 ln(2x 2 3)

dx 2

1

 

3 ln(2x 2 3)

 

d (2x 2 3);

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а) I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2x 2 3

 

4

2x 2 3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

 

 

 

 

2

 

 

 

 

2x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

б)

I x 3 ln(2x 2

3)

 

x 3 ln(2x 2 3)

 

 

 

 

 

d arctg

 

 

 

 

 

 

 

.

2(x 2 3/ 2)

 

 

 

 

 

 

 

 

 

x

3

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Работа над пунктом б) к успеху не приведет, так как при

u (x ) arctg

 

 

 

2x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

данный интеграл не напоминает ни один из табличных интегралов. В

пункте а) требуется еще одно подведение под знак дифференциала. Преоб-

разуем

интеграл в

пункте а), сделав замену

 

u 2x 2 3

и используя

du

d lnu , (см. (3.2), таблицу 1 форм. 2):

 

 

 

 

 

 

u

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

d (2x 2 3)

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3 ln(2x

2

 

 

 

3 ln(2x 2

3)d ln(2x 2

 

 

 

I

 

3)

 

 

 

 

 

 

3)

 

 

4

 

 

2x 2 3

4

 

 

 

1

 

u1/ 3du

1

 

u 4 / 3

 

3

 

 

3

 

 

 

 

 

 

 

 

 

C

u 4 / 3

C

3 u 4 C ,

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

4

4 / 3

16

 

 

 

16

 

 

 

 

 

 

 

 

где u ln(2x 2

3) . Получаем окончательный ответ.

 

Ответ: I 163 3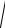ln4 (2x 2 3) C .

Замечание. Метод подведения под знак дифференциала является ос-

новным методом интегрирования. Поэтому чем больше будет решено за-

дач, связанных с ним, тем легче будет усвоить следующие методы интег-

рирования.

12

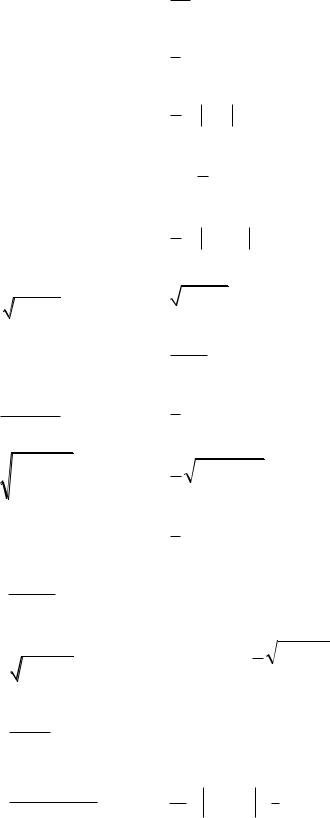
1. (4x 1)7dx

2. cos3xdx

3.

dx

sin 2x

 

4. (sinx cosx )2dx

5.

dx

 

 

 

6x 5

6.

 

dx

 

 

 

 

2x 3

 

 

7.x 3x 2 dx

8.arctg2 xdx

x2 1

9.

arcsinx

dx

 

1 x 2

10.cos3x sin2 3xdx

11.x 5 dx

x2 9

12.

3 4x

 

 

dx

 

 

 

 

1 9x

2

 

 

 

13. dx

1 ex

14. x arctg 4xdx

1 16x 2

Задачи для самостоятельной работы

Отв. 321 (4x 1)8 C

Отв. 13 sin 3x C

Отв. 12 ln tg x C

Отв. x 12 cos 2x C

Отв. 16 ln 6x 5 C

Отв. 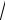2x 3 C n 1/ 2

Отв. 1 3x 2 C

2ln 3

Отв. 13 arctg3 x C

Отв. 23 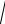arcsin3 x C

Отв. 19 sin3 3x C

 

1

 

9

 

 

5

 

x 3

 

C

Отв.

ln

 

x 2

 

ln

 

 

 

 

 

 

x 3

 

2

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

Отв. arcsin 3x 94 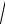1 9x 2 C

Отв. x ln(1 ex ) C

Отв. 321 ln 1 16x 2 81 arctg2 4x C

См. (3.1), таблицу 1 форм. 1

См. (3.1), таблицу 1 форм. 5

См. (3.1), таблицу 1 форм. 9

(a b)2 a 2 2ab b2

См. (3.1), таблицу 1 форм. 6

См. (3.1), таблицу 1 форм. 2

См. (3.1), таблицу 1 форм. 2

См. (3.2), таблицу 1 форм. 4

См. (3.2), таблицу 1 форм. 17 и 1

См. (3.2), таблицу 1 форм. 15 и 1

См. (3.1), (3.2), таблицу 1

форм. 1

Пример 8, таблицу 1 форм. 2 и 18

Пример 8, таблицу 1 форм. 1 и 15

1

 

1 a a

, См. (3.2),

1 a

1 a

 

 

таблицу 1 форм. 1 и 2

См. (3.1), (3.2), таблицу 1

форм. 1 и 2

13

Часть 4. Интегрирование по частям

Если интеграл можно преобразовать так, что f (x )dx u (x )dv(x ) ,

но получившийся интеграл нельзя вычислить, применяя уже рассмотрен-

ные методы, то имеет место следующая формула, называемая формулой интегрирования по частям:

u (x )dv(x ) u (x ) v(x ) v(x )du (x ) ,

(4.1)

то есть

интеграл от произведения одной функции на дифференциал другой функции равен произведению этих функций минус интеграл от произведения второй функции на дифференциал первой функции.

Пример 10. Вычислим интеграл log2xdx .

Решение. Данный интеграл не является табличным и не похож ни на один интеграл из табличных. Функцию f (x ) log2 x невозможно преобра-

зовать так, чтоб она стала табличной. Подынтегральное выражение имеет форму u (x )dv (x ) , поэтому в силу формулы интегрирования по частям (4.1)

получаем:

 

udv uv vdu , где

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

log2xdx u (x ) log2 x , dv (x ) dx ,

 

x log2 x x

 

 

x ln 2

 

 

dx

 

 

 

 

v(x ) x , dv(x ) v dx

 

 

 

 

 

 

 

 

 

 

x ln 2

 

 

 

 

 

 

 

 

 

x log2 x ln12 dx x log2 x lnx2 C .

Ответ получен.

Пример 11. Вычислим интеграл x cosxdx .

14

Решение. Данный интеграл допускает два варианта приведения к ви-

ду udv , так как под знак дифференциала можно подвести как x , так и

cosx , см. (3.2). Рассмотрим оба варианта.

а)

Подведем

под знак дифференциала x . Получим интеграл

cosxd (x 2 / 2) вида

udv . В результате применения формулы интегриро-

вания по частям получим новый интеграл вида vdu (x 2 / 2)d cosx .

б)

Подведем под знак дифференциала cosx . Получим интеграл

xd sinx

вида udv . В результате применения формулы интегрирования

по частям получим новый интеграл вида vdu sinxdx .

Из двух полученных новых интегралов проще оказался второй. По-

этому для вычисления исходного интеграла выбираем преобразования, по-

казанные в пункте б). Покажем результат применения формулы (4.1):

 

 

{ {

{ {

{

{

 

x cosxdx

x d sinx x

sinx

sinx dx .

 

 

u dv

u

v

v

du

Ответ: x sinx cosx C .

Пример 12. Вычислите интеграл lnxxdx .

Решение. (Поэтапная самопроверка.) Ответьте последовательно на

следующие вопросы.

1) Какую часть подынтегральной функции проще подвести под знак

дифференциала?

См. (3.2). (Под знак дифференциала проще подвести

1

 

 

.)

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

2) Как будет выглядеть новый интеграл?

 

 

 

 

 

 

 

(см. таблица 1 форм. 1,

ln

x

 

dx lnxd 2

 

 

 

 

x .)

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

15

3) Примените к исходному интегралу формулу интегрирования по

частям.

ln

x

 

 

 

 

 

 

 

 

 

 

 

dx 2 lnx d x 2

x lnx

 

x

 

 

 

 

 

x

 

 

{ {

 

 

 

 

{

 

u dv

 

 

 

v

d lnx . {

du

4) Новый интеграл в правой части не является табличным, можно ли его преобразовать к табличному интегралу?

 

 

 

 

 

(Можно, воспользовавшись равенством d ln x ln x dx

1

 

dx .)

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5) Выполнив преобразование из пункта г),

вычислите интеграл.

 

 

 

 

 

ln x

 

 

 

 

 

 

 

1

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx 2 x lnx

x

 

dx 2 x lnx

2

 

 

 

2 x lnx 4 x

 

C

 

 

 

 

 

 

 

 

x

 

 

 

 

x

 

 

x

 

 

 

 

 

 

 

Ответ получен.

Пример 13. Вычислите интеграл x dx . cos2 3x

Решение. (Поэтапная самопроверка.) Ответьте последовательно на

следующие вопросы.

1) Можно ли подвести под знак дифференциала x , и как тогда будет

выглядеть интеграл?

 

 

 

 

 

 

 

 

xdx

 

1

 

 

 

dx 2

 

Можно, см. (3.2)

 

 

 

 

 

 

 

 

 

 

 

 

 

.

cos2 3x

2

cos2 3x

 

 

 

 

 

 

 

 

2) Можно ли подвести под знак дифференциала

 

 

1

 

 

, и как будет

 

 

 

 

 

 

cos2

3x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

выглядеть интеграл в этом случае?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

1

 

 

 

d 3x

 

 

 

1

 

 

 

Можно, см. (3.1)

и (3.2)

 

x

 

 

 

 

 

x

 

 

 

 

 

 

 

 

xd tg 3x .

 

 

 

3

 

 

 

 

 

 

 

 

 

 

cos2 3x

 

 

 

 

cos2 3x

 

3

 

 

3) В пунктах а) и б) получены интегралы вида

 

udv . Поменяйте в

обоих интегралах функции u и v

местами и выберите для дальнейших вы-

числений тот из них, который проще.

 

 

 

 

 

 

 

 

 

 

 

vdu

1

 

2

1

 

 

 

Из пункта а) следует

 

x d

 

 

.

 

 

 

 

 

 

2

cos2

3x

16

 

 

vdu

1

 

 

 

 

3

 

 

Из пункта б) следует

 

 

 

 

tg 3xdx.

(Второй из полученных интегралов проще, поэтому для вычисления исходного

интеграла мы выбираем преобразования из пункта б).)

4) Завершите вычисление интеграла.

 

 

 

 

 

xdx

 

 

 

1

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

1

x tg 3x

 

 

sin 3x

 

 

 

 

 

 

 

 

 

 

 

x d tg 3x

(x tg 3x

tg 3x dx )

 

dx

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

cos

3x

3

{ 142 443

 

3

{

{

 

{

{

 

3

 

 

 

cos3x

 

 

 

 

 

 

 

 

u

dv

 

 

 

u

v

 

 

v

du

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

x tg3x

1

 

 

sin3x

d3x

1

 

x tg3x

1

 

d cos3x

 

1

x tg3x

1

ln

 

cos3x

 

C .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

cos3x

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

9

 

 

3

 

 

 

 

9

cos3x

 

 

3

 

 

 

9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ получен.

Существуют интегралы, для вычисления которых формулу интегрирования по частям необходимо применить несколько раз.

Пример 14. Вычислите интеграл x 2exdx , применяя метод интегри-

рования по частям.

Решение. Ответьте последовательно на следующие вопросы.

1) Какую часть подынтегральной функции можно подвести под знак

дифференциала? (Под знак дифференциала можно подвести и x 2 , и ex .)

2) Чтобы построить интеграл вида udv , рассмотрите два возмож-

ных варианта: подведите под знак дифференциала x 2 , затем ex .

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 x

dx

1

 

 

 

x

 

3

 

 

 

2 x

dx

 

 

2 x

 

 

 

 

 

 

x e

 

 

 

e

dx

 

и

 

 

x e

 

x de

, см. (3.1) и (3.2).

3) Как будет выглядеть новый интеграл вида

 

vdu

в каждом из этих

 

 

 

 

 

 

 

 

 

 

 

 

vdu

1

 

 

3

 

x

 

 

vdu

 

x

2

двух случаев?

 

 

 

 

 

 

 

 

 

 

 

 

x de

 

и

e dx

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

4) Какой из последних интегралов проще для дальнейшего вычисле-

ния?

 

 

Проще

exdx 2

ex 2xdx 2 xexdx .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

17

5) Примените формулу интегрирования по частям к исходному инте-

гралу, выбрав более простой способ подведения под знак дифференциала.x 2exdx x 2dex x 2ex exdx 2 x 2ex 2 xexdx .

6) В правой части появился интеграл xexdx , для вычисления кото-

рого снова применим формулу интегрирования по частям, подведя под

дифференциал также ex .

xexdx xdex

xex exdx xex ex C .

7) После двух применений формулы

интегрирования по частям

окончательно получаем x 2exdx x 2ex 2 xexdx x 2ex 2 xex ex C .

Ответ получен.

Существуют интегралы, применение к которым формулы ин-

тегрирования по частям приводит к уравнению относительно иско-

мого интеграла.

Разберем следующие примеры.

Пример 15. Вычислим интеграл 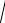a 2 x 2dx , используя метод ин-

тегрирования по частям.

Решение. Данный интеграл имеет вид udv , и если применим к нему формулу интегрирования по частям (4.1), то получим следующее:

 

 

a 2

x 2 dx x a 2

x 2

 

 

 

14442 4443{

 

{ 14442 4443

 

 

 

u

 

dv

 

v

 

 

 

u

 

 

 

 

 

 

 

x 2dx

 

 

 

 

 

x

a 2 x 2

 

2

 

.

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d

 

 

(a 2

 

 

 

 

 

a 2 x 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x d

a 2 x 2

 

 

 

 

 

 

 

 

 

 

 

 

 

2xdx

 

 

{ 144442 44443

 

 

 

 

 

.

v

 

du

 

 

 

 

 

 

 

 

 

a 2 x 2

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

x 2 ) dx

18

Последний интеграл не является табличным, и никакое подведение под знак дифференциала не приводит его к табличному виду. Преобразуем этот интеграл следующим образом:

 

 

x 2dx

 

 

 

 

 

(x 2

a 2 ) a 2

 

 

 

 

a 2 x 2

 

 

a 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

 

2

 

 

 

2

 

 

 

2

 

2

 

 

2

 

2

a

x

 

 

 

 

a

x

 

 

 

 

 

a

x

 

 

a

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a 2 x 2dx a 2

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

2

x

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тогда для исходного интеграла мы имеем следующее уравнение:

 

 

 

dx x

 

a 2

 

 

dx

 

 

 

 

dx .

a 2 x 2

a 2 x 2

 

 

 

a 2 x 2

 

 

 

 

 

 

 

a

2

2

 

 

 

 

 

 

x

 

 

 

 

 

Перенесем последнее слагаемое в левую часть и выразим искомый интеграл:

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

x

2

dx

 

2

x

2

a

2

 

x

 

 

2

x

2

 

C .

a

 

 

 

x a

 

 

 

ln

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ получен.

Пример 16. Вычислим интеграл ex sinxdx , применяя метод интег-

рирования по частям.

Решение. В данном интеграле под знак дифференциала можно подвести и ex , и sinx :

а) ex sinxdx sinxdex ; б) ex sinxdx exd cosx .

Если в обоих интегралах вида udv поменять функции u и v места-

ми, то интегралы вида vdu будут выглядеть следующим образом:

а) vdu exd sinx ; б) vdu cosxdex .

Нельзя сказать какой из них проще, поэтому для вычисления исход-

ного интеграла может быть выбрано любое из этих преобразований. Пре-

19

образуем интеграл и применим к нему формулу интегрирования по частям

(4.1):

 

 

d sinx (sinx ) dx

 

ex sinxdx sinxdex ex sinx exd sinx

cosxdx.

 

ex sinx ex cosxdx.

Впоследнем интеграле подведем под знак дифференциала функцию

ex , а затем применим снова формулу интегрирования по частям:

 

 

 

 

 

 

 

 

 

 

 

d cosx (cosx ) dx

 

 

ex cosxdx cosxdex ex cosx exd cosx

 

 

 

sinxdx.

 

 

 

ex cosx ex sinxdx.

 

 

 

Тогда для исходного интеграла получим следующее уравнение:

 

 

 

ex sinxdx ex sinx ex cosx ex sinxdx.

 

 

 

Из данного уравнения выразим исходный интеграл:

 

 

 

ex sin x

1

ex (sin x cosx ) C .

 

 

 

 

 

 

 

2

 

 

 

 

Ответ получен.

 

 

 

Задачи для самостоятельной работы

1. arcctgxdx

Отв. x arcctgx

 

1

ln(x 2

1) C

См. (4.1)

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.

x 2 ln xdx

Отв.

1

 

x 3 lnx

1

x 3 C

 

См. (3.2) и (4.1)

 

 

 

 

 

 

 

 

3

 

 

 

9

 

 

 

 

 

3.

 

log2 x

dx

Отв.

 

1

log

2

x

1

C

См. (3.2) и (4.1)

 

 

 

 

 

 

x 2

 

 

 

 

x

 

 

 

 

 

x ln 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.

xe3xdx

Отв.

1

xe3x

 

1

e3x C

 

 

См. (3.2) и (4.1)

 

 

 

 

 

 

 

 

 

3

 

 

 

9

 

 

 

 

 

 

 

 

20

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности