integraly_-_vse_(1) (1)

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Пример 17. Вычислим интеграл

.pdf

Скачиваний:

Добавлен:

23.03.2016

Размер:

1.06 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

x sin 2xdx

Отв.

x cos 2x

sin 2x C

См. (3.2) и (4.1)

x 2 cosxdx

Отв. x 2 sin x

2x cosx sin x C

См. (3.2) , (4.1) и

пример 14

2x sin xdx

Отв.

ln 2 sinx cosx

2x C

См. пример 16

1 ln

coslnxdx

Отв.

x (cos ln x sin ln x ) C

См. (4.1)

x cosx

Отв.

ctgx

См. (3.2) и (4.1)

sin3 x

2sin2 x

Часть 5. Метод подстановки (замена переменной)

Если интеграл f (x )dx нельзя взять, применяя ранее предложенные

методы, причем в подынтегральной функции есть часть (x ) , которая вы-

глядит “инородной”, то можно попробовать ввести новую переменную

(x ) t . Выразим переменную x (t ) , вычислить дифференциал dx (x )dt и подставить в подынтегральную функцию, то исходный ин-

теграл преобразуется следующим образом:

f (x )dx f ( (t )) (t )dt f *(t )dt.

Если получившийся интеграл можно вычислить, то

f (x )dx F *(t ) C F *( (x )) C ,

где F *(t ) – первообразная функции f *(t ) , подставив в которую

t (x ) , получаем ответ.

Рассмотрим несколько примеров, в которых используется данный

метод.

Решение. Данный интеграл не является табличным, не похож ни на один из табличных интегралов. Используя свойства интегралов невозмож-

но представить этот интеграл в виде суммы табличных интегралов. В по-

дынтегральной функции отсутствует часть, которую можно было бы под-

вести под знак дифференциала. Данный интеграл нельзя вычислить, ис-

пользуя формулу интегрирования по частям. Попробуем упростить подын-

тегральную функцию, заменив ее знаменатель новой переменной t :



						2				3x 1 t ,					2
									(t 2)2						2	(t 2)			t 2
			dx						(t 2)2						3	(t 2)	2		t 2
															3		dt
	2					x						,						3		t	dt .
	2			3x 1		x				3		,				t		3		t	dt .
										2
						dx				2	(t 2)dt
						dx					(t 2)dt
										3
Последний интеграл легко вычисляется.
	t	2					2
	t	2					2

		t					t
			dt		1			dt t 2ln					t	C .

Вернувшись к старой переменной t 2 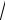3x 1, окончательно по-

лучаем:

	dx		2	2				C .
					3x 1 2ln	2	3x 1

2
		3x 1	3

Ответ получен.

Пример 18. Вычислите интеграл cos 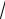xdx .

Решение. (Поэтапная самопроверка.) Ответьте последовательно на

следующие вопросы.
1) Является ли данный интеграл табличным?	(Нет.)
2) Похож ли он на один из табличных интегралов?

(Похож на интеграл cosudu .)

3) Можно ли какую-либо часть подынтегральной функции подвести

под знак дифференциала?	(Нет.)
	22

4) Сделав замену 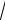x t , преобразуйте данный интеграл.

t , x t 2

cos xdx

dx 2tdt .

t costdt .

5) Знаком ли вам последний интеграл? Каким методом можно его

вычислить? (Методом интегрирования по частям, см. часть 4.)

6) Применив нужный метод интегрирования, вычислите интеграл.

t costdt	{ {	{	{	{ {	t sint cost C .
t costdt	t d sint t		sint	sint dt	t sint cost C .
	u dv	u	v	v du

7) Не забудьте вернуться к старой переменной.

Ответ: 2 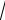x sin x cos x C .

Задачи для самостоятельной работы

1. x (2x 3)7dx

2.		dx

	x 2
	x 2

3.e x dx

4.e 3x dx

5. x 1 dx

1 3 x 1

6 xdx

43 x 1

7. 1 34x dx

8. 2 5x dx

4 5x

Отв. (2x 3)9 3(2x 3)8 C 36 32

Отв. 2 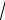x 2 2ln(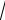x 2) C

Отв. 2 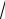xe x e x C

Отв.e 3x 33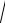x 2 63x 6 C

Отв. 76 6(x 1)7 65 6(x 1)5 23x 1

66x 1 arctg 6x 1 C

		3		1		3	6		3
			6 x 5
Отв.					x			x		arctg 26 x C

	10			8		32			64
	10			8		32			64

Отв. x 103 6(4x )5 C

Отв. 158 4(5x )3 254 4(5x )5 C

2x 3 t

x 2 t

x t

3x t и (4.1)

6x 1 t

6x t

64x t

45x t

u x x0 .

Часть 6. Интегрирование некоторых функций,

содержащих квадратный трехчлен

Рассмотрим некоторые интегралы вида							f (x, ax2 bx c)dx и способы
их вычисления.
			dx		1
1.					, k	,1	(6.1)
1.	(ax	2	bx c)	k	, k	,1	(6.1)
	(ax		bx c)		2

Для вычисления интеграла такого вида достаточно выделить полный квадрат в квадратном трехчлене ax2 bx c a(x x0 )2 B , что приведет к табличному интегралу при

		mx n			dx ,	1
2.						k	,1	(6.2)
	(ax	2	bx c)	k
						2

Для вычисления интеграла такого вида существует два способа.

Первый способ. Выделив полный квадрат, преобразовать квадратный

трехчлен так, что ax2 bx c a(x x )

2 B , и затем заменить x x

t .

Второй способ. Тождественно преобразовать числитель mx n , вы-

делив в нем слагаемое,

равное

производной

квадратного

трехчлена

(ax2 bx c) 2ax b . Пользуясь тем,

что u dx du , подвести это слагаемое

под знак дифференциала.

(2ax b) n

mx n

(2ax b)dx

(ax2 bx c)k

)

(ax2 bx c)k

Первый интеграл справа приводится к

. Второй интеграл имеет

вид, рассматриваемый в (6.1).

, N

(6.3)

(mx n)

ax2 bx c

Для вычисления интеграла данного вида существует стандартная

подстановка mx n

, которая приводит этот интеграл к одному из преды-

дущих видов (6.1) или (6.2).

(x)dx

, где Pn

(x) - многочлен порядка n .

(6.4)

ax2

bx c

Для

вычисления

данного

интеграла

полагаем,

что

Pn (x)dx

(x) ax2

bx c

где

многочлен

ax2 bx c

n 1

ax2

bx c

(x) Axn 1

Bxn 2 ... C

имеет неопределенные коэффициенты, которые

n 1

вместе с числом можно найти, продифференцировав обе части равенства

и приравняв коэффициенты при одинаковых степенях x в получившемся

выражении.

Замечание. Одно из свойств неопределѐнного интеграла, вытекаю-

щее из его определения, заключается в том, что dxd f (x)dx f (x) .

Рассмотрим несколько примеров.

Пример 21. Вычислим интеграл J		dx


	5	4x x	2
	5	4x x

Решение. Данный интеграл не является табличным, но похож на ин-

теграл 15 таблицы 1, интеграл такого вида был рассмотрен в пункте (6.1).

Выделим

полный

квадрат

подкоренном

выражении

5 4x x2 (x2 4x 4) 4 5 9 (x 2)2 .

Тогда J

d (x 2)

. (См.(3.1)).

(x 2)

9 (x 2)

Новый интеграл является табличным при u x 2 .

(См. таблицу 1

форм. 15).

Ответ:

J arcsin

x 2

C .

3x 4

Пример 22. Вычислим интеграл

dx .

x2 7x 10

Решение. (См.(6.2)).

Первый способ. Выделим в квадратном трехчлене полный квадрат

	2		2		7	7 2	49		7		2	9	.
x		7x 10 x		2x				10 (x		)
x		7x 10 x		2x				10 (x		)
					2	2	4		2			4

Произведем замену

3x 4

J x2 7x 10

	7
x		t
x	2	t
	2
			7
dx x t			7
dx x t
			2
	dt
dx	dt

переменных так,									что			x		7	t . Тогда
переменных так,									что			x		2	t . Тогда
														2
			7
3	t				4		tdt		13		dt
3	t		2		4
			2			dt 3							.
		t2		9			t2	9		2	t2	9	.
		t2		4			t2	4			t2	4
				4				4				4

Получили два, достаточно просто вычисляющихся интеграла:

															d (t2							9		)
		tdt							1						d (t2							4		)					1			ln			t2					9		C				. (См. (3.2) и (3.1)).
		tdt							1													4							1											9
t										2
					9																9					2											4						1
		2			9											t2					9					2											4
		2														t2
					4															4
																			t				3
																							3
			dt									1				ln
			dt									1											2			C2 . (См. таблицу 1 форм.18).
		2			9					2			3						t				3			C2 . (См. таблицу 1 форм.18).
		2			9								3										3
	t
	t				4								2										2
					4								2										2
И окончательно, получаем
																																																			t	3
																																																				3
J							3x 4																			1										2	9					13				1						2
																			dx 3												ln			t															ln				C
				x2 7x 10															dx 3									2			ln			t					4				2				3		ln		t	3	C
																																																			t	2
																																					2(x						7		)	3
																																											7
						3										7				2			9				13																2
								ln			(x								)														ln																	C
						2		ln			(x						2		)						4					6			ln				2(x						7	)		3				C
																																					2(x						2	)		3
Ответ: J														3								7x 10																13					x 2					C .
																ln		x2																							ln

																																											x 5
													2																								6
													2																								6

Второй способ. Тождественно преобразовав числитель, выделим в нем производную квадратного трехчлена (x2 7x 10) 2x 7 .

3x 4	3	(2x) 4	3	(2x 7)	3 7	4	3	(2x 7)	13	.
	2		2		2		2		2

Тогда данный интеграл можно представить как разность двух инте-

гралов:

		3	(2x 7)	13
3x 4						3	(2x 7)dx	13	dx
3x 4		2		2		3	(2x 7)dx	13	dx
	dx				dx					.
x2 7x 10	dx		x2 7x 10		dx	2	x2 7x 10	2	x2 7x 10	.

В первом из полученных слева интегралов подведем числитель под знак дифференциала (см. (3.2))

(2x 7)dx

d (x2 7x)

d (x2 7x 10)

7x 10

C1 .

x2 7x 10

Второй интеграл приводится к табличному путем выделения полного квадрата (см. (6.1))

x 2

C2 .

x2 7x 10

x 5

)

Окончательный ответ совпадает с уже полученным

3x 4

x 2

C .

7x 10

x2 7x 10

x 5

Пример 23. Вычислите

интеграл

, ответив после-

(x 1)

x2 2x 2

довательно на поставленные вопросы.

Решение. 1) Является ли данный интеграл табличным?

(нет)

2) Можно ли часть подынтегральной функции подвести под знак

дифференциала и относительно некоторой новой переменной u свести ин-

теграл к табличному? (Можно подвести под знак дифференциала x1 1 ,

но новый интеграл не будет табличным).

3) Что существенное содержит подынтегральная функция в свете


рассмотренных нами способов интегрирования?	(Квадратный трехчлен)
4) К какому пункту части 6 относится данный интеграл?		(6.3)

5) С чего следует начать преобразование данного интеграла, чтобы

привести его к табличному виду? (Необходима подстановка x 1 1t (см. (6.3)).

6)	Преобразуйте интеграл выбранным способом.				dt


			1		4t t			2
			1		4t t
7)	Является ли полученный интеграл табличным?						(нет)
8)	Каким образом его можно привести к табличному?
	(Выделить полный квадрат. См.(6.1)).
9)	Преобразуйте полученный интеграл выбранным способом.
				dt
				dt				.


		(t 2)				2	3
		(t 2)					3

10) Вычислите полученный интеграл и выпишите окончательный от-

вет.

(Не забудьте вернуться к исходной переменной x !)

2x 1 x2

2x 2

C .

Ответ: J ln

t 2

1 4t t 2

C ln

x 1

Пример 24. Вычислим интеграл

2x3 x2 1

dx .

Решение. (См.(6.4)).

Данный интеграл имеет вид

Pn (x)

dx ,

где P (x) 2x3

есть

ax2 bx c

многочлен порядка n 3 . Следуя предложенному способу, допустим,

что

этот интеграл

2x3 x2 1

(x)

2x 5

x2 2x 5

n 1

x2 2x 5

где Q

(x) Q (x) Ax2

Bx C

- многочлен порядка n 1 2 , с неопре-

n 1

деленными коэффициентами и - некоторое число. Далее продифферен-

цируем обе части полученного равенства, учитывая, что

dxd f (x)dx f (x) .

Результатом дифференцирования будет новое равенство следующего

вида.

x3 x2 1

(2Ax B)

Ax2 Bx C

2x 2

x2 2x 5

2 x2 2x 5

x2 2x 5

Умножив обе части на

x2 2x 5 , получим

2x3 x2 1 (2Ax B) (x2

2x 5) Ax2 Bx C (x 1)

(*)

Так как равенство (*) имеет место для любого значения x , (заметим,

что функция f (x)

2x3

x2 1

определена для любого x R ), коэффициен-

2x 5

ты при одинаковых степенях x в обеих частях (*) должны быть равны. Это позволяет составить систему для нахождения чисел A, B, C и . Приравня-

ем коэффициенты при x3 , x2 , x			и x0 1 слева и справа в (*)
x3		2 2 A A
x2 1 B 4 A A B
x2 1 B 4 A A B			решая полученную систему, найдем
			решая полученную систему, найдем
x 0 10 A 2B B C
x	0	1 5B C
x		1 5B C

A 23 , B 76 ,C 196 и 8.

Теперь исходный интеграл равен

	2			7		19					dx
	2		2	7		19		2			dx
J		x			x		x		2x 5	8		.


	3			6		6					x2 2x 5

Выделив в последнем слагаемом полный квадрат (x 1)2 4 в подко-

ренном выражении, получаем ответ:

2x 5 8 ln

x 1

2x 5

C .

Задачи для самостоятельной работы

См. (6.1)

Отв.

x 2

x2 4x 13

C .

4x 13

Отв.

arcsin

x 1

C .

См. (6.1)

4x 2x

3. 3x2 12x 16

3 x

5. 2x2 5x 2 dx

6. (x 2)x2 6x 8dx

7.				dx


	(x 2)				x	2	3x
	(x 2)				x		3x
8.				dx


	x	2	1 6x 3x					2
	x		1 6x 3x

9. 3x3 x2 2x dx

4 x2

10. 4x2 x 1dx x x2


Отв.				1				arctg							3(x 2)							C .


	2			3											2
																									3

Отв. 2					x2 3x 4 2 ln																x						x2 3x 4					C
Отв. 2					x2 3x 4 2 ln																x				2		x2 3x 4					C
																									2
Отв.		17					ln		x 1 2								1		ln		2x2 5x 2										C .


										x 2
	2														4
	2														4
	1																			1									2
	1							2										3		1									2
								x 6x 8										3					(x 3) x 6x 8

			3																		2
Отв.											1
											1	ln		x	3							x		2	6x	8				C
												ln		x	3							x			6x	8				C
				1							2				x 6
											2
Отв.									arcsin												C .
													3(x 2)
				2
				2

Отв.						1 6x 3x2										3ln					1 3x 1 6x 3x2												C
Отв.										x						3ln												x					C
										x																		x

Отв. (x2 2x 6)4 x2 8arcsin 2x C .

Отв. 2(x 1)x x2 2arcsin(2x 1) C

См. (6.1)

См. (6.2)

См. (6.2) и

таблицу 1,

форм.20

См. (6.3)

См. (6.3), и

замена 1x t

См. (6.4)

Часть 7. Интегрирование рациональных дробей

P (x)

n 2

Рассмотрим

интеграл

вида

dx ,

где

(x)

P (x) a xm a xm 1 ... a

, Q (x) b xn b xn 1 ... b

- многочлены степени m

соответственно,

и подынтегральная дробь является несократимой. Для

интегрирования несократимой дроби

(x)

необходимо следующее еѐ пре-

(x)

образование, вытекающее из основных теорем алгебры.

	Таблица 2.

Условие	Преобразование

m n	Выделение целой части (то есть деление многочлена Pm (x) на

	30

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.201516.04 Кб14inflation.docx
#
16.09.201929.77 Кб16Informatsionnye_tekhnologii_v_istoricheskikh_is...docx
#
09.02.2015670.72 Кб26Innov_prots.doc
#
09.11.2018321.02 Кб5INSTR.DOC
#
10.02.2015659.25 Кб19integral.pdf
#
23.03.20161.06 Mб13integraly_-_vse_(1) (1).pdf
#
13.07.201922.72 Кб7inzhenerka (1).docx
#
09.02.201576.29 Кб127InzhGraf_otvety.doc
#
09.02.201556.83 Кб14inzhRK.doc
#
23.03.20163 Mб62Ispravlenny_otchyot.docx
#
17.04.2019667.77 Кб7itogovaya_shpora.docx