
УчебникНГ_полный
.pdf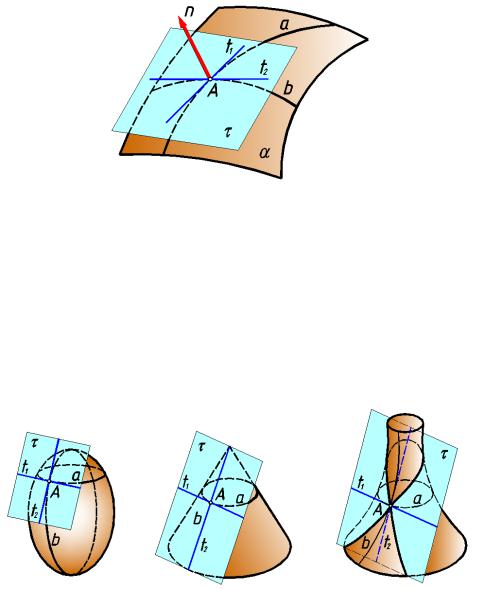
Прямой, касатель ной к поверхности называется прямая, касательная к какой-ли бо кривой, принад лежащей поверхности.
Нормалью к пове рхности в заданной точке называют прямую, перпендикулярную касательной плоскости в данной точке. С помощью нормали определяю кратчайш ее расстояние от внешней т очки до поверхности.
Посколь ку плоскость одноз начно задается двумя пересекающимися прямыми, то, для задания касательной плоскости в некоторой точке А поверхности, следует через эту
точку провести на поверхности две линии а и b и построить к ним касательные t1 и t2
(рис.226).
Если на поверхности через точку мо жно провести прямую линию, то она будет прин адлежать касательной плоскости к повер хности в данной точке.
рис. 226
Взаимное положение касательной плоскости и поверхн ости может быть трех
видов:
1.Касательная пл оскость может иметь с поверхностью только одну общую точку. Такая поверхность называется поверхностью с элл иптически ми точками
(рис.227).
2.Касательная плоскость может касаться поверхности по линии. Такая поверхность называется п оверхностью с параболическим и точками (рис.228).
3.Касательная плоскость может пересекать поверхность. Такая поверхность называется поверхностью с гиперболическими точками ( рис.229).
рис. 227 |
рис. 228 |
рис. 229 |
Существуют поверхности, имеющие несколько различных типов точек. Например, поверхность открытого тора обладает точками всех трех типов: на наружной части поверхности находятся точки эллиптического типа, на внутренней части поверхности — точки гиперболического типа, на границе внешней и внутренней частей поверхности — точки параболического типа.
131
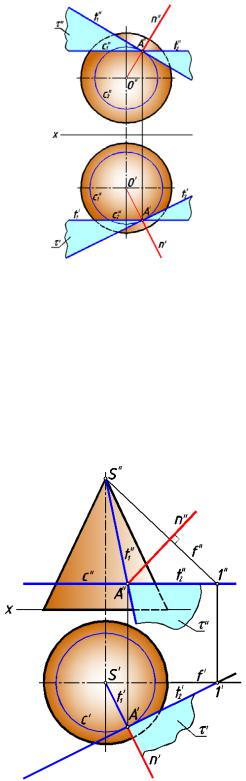
Рассмотрим построение проекций касательной плоскости и нормали к поверхности сферы (рис.230 ).
Через т очку А на с фере можно провести касательные t1 и t2 к двум окружностям с1
и с2 , проходящим на поверхности |
через точку |
А и параллельных горизонтальной и |
фро нтальной п лоскостям проекций . |
Касательная |
к плоской кривой лежит в плоскости |
этой кривой. |
|
|
Нормаль n к сфере всегда проходит чер ез центр сферы.
рис. 230
Построение проекций касательной плоскости и н ормали к поверхности конуса д ано на рис.231.
Плоскость касается кони ческой по верхности по образующей t1, которая прин адлежит касательной плоскости. Достаточно провести ещё касательную t2 к окружности с, проходящей через точку А.
Для проведения нормали n через точку А проводим перпендикуляр к касательн ой плоскости (фронтальная проекция нормали перпенд икулярна фронтальной проекции фро нтали касательной плоскости).
рис. 231
132
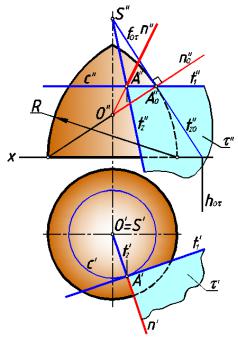
Рассмотрим построение проекций касательной плоскости и нормали к поверхности тора (рис.232).
Для построения касательной плоскости, проходящей через точ ку А на торе достаточно провести касательные к двум линиям, проходящим на поверхности через точку А. Одной из
таких линий является параллель с — окружность, параллельная горизонтальной плоскости проекций. Вторая линия — меридиан поверхно ти (дуга окружности радиусом R ).
Построи ть касательную t1 к параллели с не сложно.
Меридиан поверхности не паралле ен фронтальной плоскости проекций и проецируется на нее дугой эллипса. Чтобы избе жать построения лекальной кривой, используем способ преобразования чертежа — вращение вокруг проецирующей прямой. Ме идиональную
плоскость вместе с точкой |
А повернем вокруг оси поверхности |
в положение главной |
меридиональной плоскости. |
Меридиан, проходящий через точку А, |
совместится с главным |
меридианом, а точка А займет положение А0. Касательная t20 к главному меридиану в точке А0 пересекает ось поверхности в точке S. Поскольку точка S при вращении вокруг оси тора
неподвижна, токасательнаяt2 кповерхностипройдетчерезэтуточку.
Заметим , что п лоскость τ, касательная к поверхности тора в точке А0 перпендикулярна фронтальной плоскости проекций. Фронтальная проекция нормали n0 к поверхности в точке А0 перпендикулярна фронтальному следу f0τ касательн ой плоскости. Нормаль n0 пересекает ось поверхн ости в точ ке О, через которую проходит фронтальная проекция n" нормали к поверхности в точке А .
рис. 232
Вопросы для самопроверки
¾Какая прямая называется касательной к поверхности в заданной точке?
¾Какая плоскость называется каса тельной к поверхност и в заданной точке?
¾Какая прямая называется нормалью к поверхности в заданной точке?
¾Каким может быть взаимное положение поверхности и касательной к ней плоскости?
¾Как на черте же задать касательную плоскость к поверхности?
¾Как построить проекции нормали к поверхности?
¾ Как построи ть проекц ии нормали к поверхности вращения без построения касательной плоскости?
133
§42. ПОСТРОЕНИЕ ОЧЕРКА ПОВЕРХНОСТИ ВРАЩЕ НИЯ, ОСЬ КОТОР ОЙ НАКЛ ОНЕНА К ПЛОСКОСТИ ПРОЕКЦИЙ
Если ось |
поверх ности вра щения наклонена к |
плоскости |
проекций, то на |
эту |
||||||||||||
плоскость поверхность проецируется с искажением. |
|
|
|
|
|
|
|
|
||||||||
Рассмотрим построение |
очерковых |
образую щих |
кон ической |
поверхности |
||||||||||||
вращ ения, ось которой |
параллельна фронтальной плоскости проекций, |
но наклонена к |
||||||||||||||
горизонтальной плоскости проекций (рис.233). |
|
|
|
|
|
|
|
|
|
|||||||
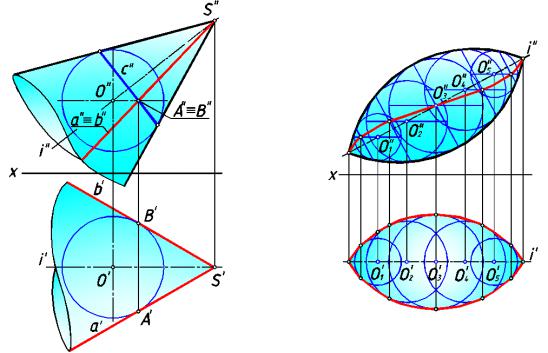
На оси конуса выб ираем произвольную |
точку О и, взяв её за центр сферы, впишем |
|||||||||||||||
сферу, касающуюся конической поверхности по параллели с. |
|
|
|
|
|
|
|
|||||||||
Образу ющими |
конуса, |
являющимися |
очерковыми |
при |
проеци ровании |
на |
||||||||||
горизонтальную |
плоскость |
проекц ий, |
будут |
образующие, по которым |
горизонталь но |
|||||||||||
проецирующие |
плоскости |
касаются |
конической поверхности. |
Эта |
плоскости будут |
|||||||||||
касаться вписанной сферы в точках А и |
В, |
лежащи х на |
экваторе |
сферы. Искомые |
||||||||||||
касательные а и b проходят через точки А и В и вер шину конуса S. |
Горизонтальные |
|||||||||||||||
проекции этих прямых задают очерк ко ической |
поверхности |
на |
горизонтальн ой |
|||||||||||||
плоскости проекций, |
а |
их |
фронтальные |
проекции |
определяю т |
границу видимости |
||||||||||
поверхности на ее горизонтальной проекции |
|
|
|
|
|
|
|
|
|
|
||||||
Следует |
обратить |
внимание, |
что угол |
между |
очерковыми |
образующими |
на |
|||||||||
фро нтальной плоскости проекций отличается от угла между очерковыми образующими на горизонтальной плоскости проекций.
На рис.234 задана поверхность вращения, ось которой параллельна фронтальн ой плоскости проекции, но н аклонена к горизонтальной пло скости проекций. Для построе ния горизонтального очерка этой поверхности используют следующий прием. В поверхность вписывают ряд сфер, центры которых находятся на оси поверхности. Постр оив горизонтальные проекции этих сфер, проводят кривую линию, огибающу ю эти сферы. Построенная кривая является горизонтальным очерком п оверхности.
рис. 233 |
рис. 234 |
Вопросы для самопроверки
¾ Как построить очерковые образующие конуса вращения, ось которого наклонена к одной из плоскостей проекций?
134
Глава VI II
МЕТР ИЧЕСКИЕ ЗАДАЧИ
К метрическим задачам относятся задачи на определен ие расстояний и углов
между геометрическими фигурами, а также задачи на построение о трезка и угла с наперед заданным значением, соответственно, линейн ой и градусной величины.
В основе алгорит ма решения любой метрической задачи лежит третий инвариант ортогонального проецирования:
Φ &π1 Φ′ Φ
или
Φ&π2 Φ′′ Φ
§4 3. ОПРЕДЕЛЕНИЕ РАС СТОЯНИЙ
Расстояние между геометрическими фигурами определяется величиной кратчайшего отрезка прямой между двумя точками, принадлежащими этим фигурам.
Длину отрезка прямой мо жно |
определить различными способами: построен ием |
|
прямоугольного треугольника (рис.46, 47), |
замен ой плоскостей проекц ий (рис.100), вращен ием |
|
вокруг проециру ющей прям ой (рис.108 ). |
|
|
43. |
1. Расстояние от то чки до прямой линии |
|
Расстояние от точки |
до прямой линии равно длине перпендикуляра, опуще нного из точки |
|
на эту прямую. |
|
|
рис. 35 |
рис. 236 |
рис. 237 |
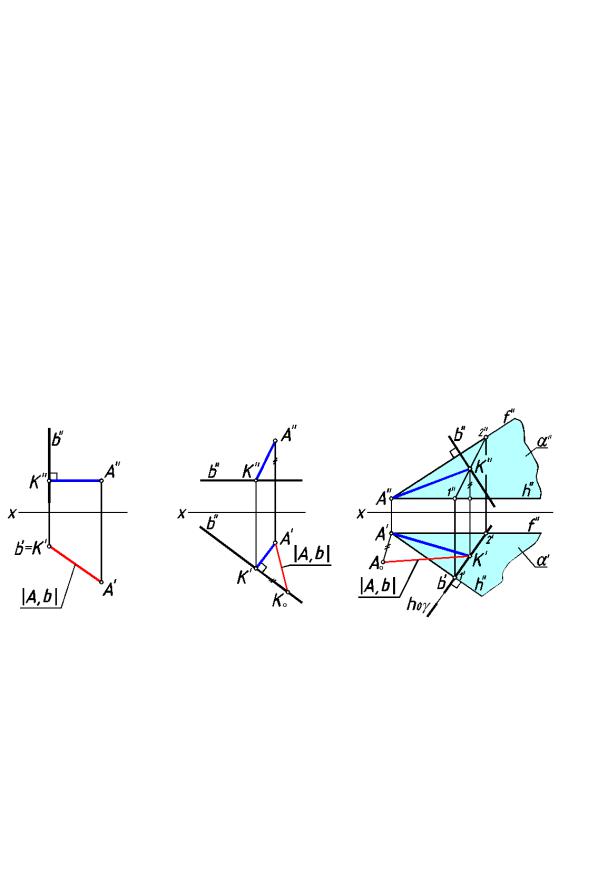
На рис.235 отрезок АK является перпендикуляром, опущ енным из точки А на
прям ую b. На горизонтальную плоскость проекции π1 он проецируется в натуральную величину.
На рис.236 прямой угол между АK и прямой b проецируется без искажения (на основании теоремы о частном случае проецирования пря мого угла). Перпендикуляр АВ на обе плоскости проекций проецируется с искаж ением.
На рис. 237 для проведения перпендикуляра к прямой b общего положения из точ ки
А следует сначала через точку А провести пл оскость α, перпендикулярную прямой b. Эта плоскость является мно жеством п рямых, пр оходящих через точку А и составляющих с
прям ой b угол 90°. Точка K пересечения прямой b с п лоскостью α является основанием перпендикуляра, опущенного из точ ки А на прямую b.
135

43.2. Расстояние от точки до плоскости
Расстояние от точ ки до пло скости равно длине перпендикуляра, опущенного из точки на эту пл оскость.
На рис.238 плоскость α перпендикулярна горизонтальной плоскости проекций.
Отрезок АК, определяющ ий расстояние от точки А до плоскости α, параллелен плоскости проекций π1 и проецируется на неё в натуральную величину.
На рис.239 плоскость α занимает общее положение относительно плоскостей проекций. Поэтому целесообразно, сначала заменой плоскостей проекций преобразовать
чертеж так, что бы плоскость стала перпендикулярна новой плоскости проекций π3.
рис. 23 8 рис. 239
4 3.3. Расстояние от точки до поверхности |
|
|
|
|
||
Расстояние от точки до |
поверхности определяется |
величин |
ой |
нормали, |
||
проведенной из точки к поверхности |
. |
|
|
|
|
|
Опреде ление расстояния от точки |
до поверхности вращения рассмотрим на |
|||||
при мере определения расстояния |
от точки |
А до конической |
поверхности |
|
враще |
ния |
(рис.240). |
|
|
|
|
|
|
рис. 240
Нормаль к поверхности вращения расположена в меридиональной плоскости, проходящей через ось поверхности вращения.
136
Для |
решения |
данной |
задачи удобнее |
всего использов ать спос об |
враще ния |
||
вокруг проецирующей прямой. |
Меридиональную плоскость, |
которой принадлеж ит |
|||||
норм аль, |
поворотом |
во круг |
оси |
поверхности |
совмещаем с |
плоскостью |
главного |
мери диана. Точка А пер ейдет в новое положение Ао. Перпендикуляр, о пущенный из фро нтальной проекции точки Ао н а очерковую образующую конуса равен расстоянию от точки А до поверхности.
43.4. Расстояние между параллельными прямыми
Расстояние между параллельными прямыми изм еряется длиной перпендикуляра, опу щенного из произволь ной точки одной прямой на другую.
Из определения ясно, что решение задачи сводится к нах ождению расстояния от точки до прям ой.
43.5. Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми линиями определяется отрезком прям ой, заключенным между этими прямыми и перпендикулярным к обеим прямым.
Такой перпендикуляр можно провести лишь один.
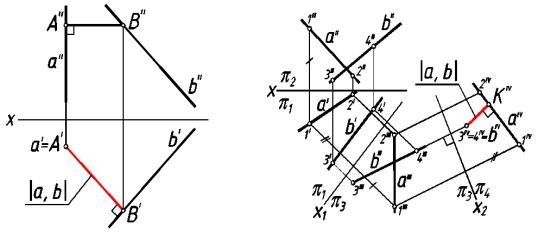
На рис. 241 представлен случай, когда одна из скрещивающ ихся прямы х а занимает
проецирующее положение относительно плоскости π1, а вторая прямая b — общего положения. Отрезок АВ перпендикулярен обеим прямым (частный случай проецирова ния прям ого угла) и параллелен горизонтальной плоскости проекций. С ледовательно,
горизонтальная проекция отрезка А'В' равна расстоянию между прямыми а и b.
рис. 241 |
рис. 242 |
На рис. 242, где скрещиваю щиеся прямые а и b занимают общее положе ние относительно плоскостей проекций, последовательной заменой двух плоскостей проекций чертёж преоб разован так, что одна из заданных скрещивающихся прямых b заняла
положение перпендикулярное новой плоскости проекций π4. Перпендикуляр к обеим скрещивающимся прямым определяет расстояние между ними.
Еще один подход к решению задачи состоит в следующем. Две скрещивающиеся прям ые можно заключить в единственную пару параллельных плоскостей , расстоя ние между которыми будет равно расстоянию между этими скрещивающимися прямыми. Либо одну из прямых заключить в плоскость, параллельную второй прямой, и на йти расстояние ме жду этой плоскостью и параллельной ей прямой.
137
43.6. Рассто яние между параллельными прямой и плоскость ю
Расстояние между прямой и параллельной ей плоскостью определяется величин ой перпендикуляра, опущенного из произвольной точки прямой на плоскость.
43.7. Расстояние между параллельными плоскостями
Расстояние между параллельными плоскостями определяется величин ой перпендикуляра, опущенного из точки, взятой на одной из плоскостей, на другую плоскость.
Вопросы для самопроверки
¾Какие задачи относятся к метрическим?
¾Что называет ся расстоянием меж ду двумя геометрическими фигурами?
¾Каким способом можно определить длину отрезка пря мой?
¾Как измерить расстояние от точки до прямой линии, о т точки до плоскости, от точки до поверхности?
¾Как измерить расстоян ие между параллельными прямы ми?
¾Как определяется расстояние между скрещивающимися прямыми?
¾ Как |
измерить расстояние между параллельными прямой и плоскостью, |
меж |
ду параллельными плоскостями? |
§44. |
ОПРЕ ДЕЛЕНИЕ ВЕЛИЧ ИН УГЛОВ |
|
Опреде ление угла |
между прямой |
и пло скостью, двумя плоскостями, |
скрещивающимися прям ыми сводится к нахо |
дению угла между двумя прямыми. |
|
44.1. Угол меж ду пересекающимися прямыми
Угол между пересекающимися прямы ми проецируется на плоскость проекций без искажения, когда плоскость этого угла параллельна плоскости проекций.
Проще всего задача решается враще нием плоскости угла вокруг линии уровня
(рис.243).
рис. 243
138

44.2. Угол между скрещ ивающим ися прямыми
Угол между скре щивающимися прямы ми определяется величиной плоского угла, образованного пересекаю щимися прямыми, параллельными зада нным скрещивающи мся прям ым.
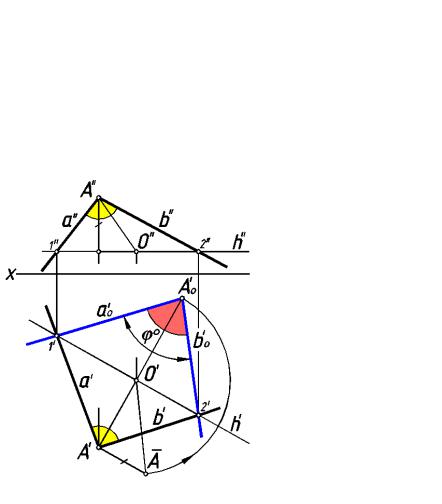
На рис.244 представлено решение задачи по определению угла меж ду скрещивающимися прямыми а и b. С этой целью через точку А на прямой b проведена прям ая с, параллельная прямой а. В еличина угла φ° ме жду пересекающимися прямыми а и c определяет величину угла между скрещивающимися прямыми аи b.
Для определения величины угла φ° использовано вращение вокруг фронтали f. Совпадение проекций с' и а' позволяет избежать лишних п остроений.
рис. 244
44.3. Угол между прямой и плоскостью
Угол между прямой а и пл оскостью α определяют величиной острого угла φ° между этой прямой и её п роекцией аα на данную плоскость (рис.245).
Для нахождения |
проекции |
прямой а на плоскость α нужно: найти точку В |
пересечения пр ямой α с |
плоскостью |
α, затем из произвольной точки А прямо й а провести |
прям ую n, перпендикулярную плоскости α, и найти точку Аα пересечения этой прямо й n с плоскостью α. Через найденные точки В и Аα провести прямую аα, которая будет
проекцией а прямой на плоскость α.
Если решать задачу по излож енной схеме, то решение будет довольно сложным.
139

рис. 245 |
рис. 246 |
Из рис.2 45 видно, что угол γ° между прямой а и п ерпендикуляром n к плоскости α, |
|
проведенным через произвольную точку А прямой а, равен 90° — |
ϕ°. Поэтому реше ние |
задачи можно упростить следующим образом: |
|
1)на прямой выбрать произвольную точку А;
2)через выбранную точку А провести п рямую n, перпендикулярную плоскости α;
3)определить величину острого угла γ ° между заданной прямой а и проведенн ой прям ой n;
4)определить величину острого угла ϕ° = 900 - γ°.
Применение изложенного способа позволяет из бежать решения двух трудоемких задач нахождения точек пересечения прямых а и b с плоскостью α.
На рис. 246 представлено ре шение задачи по определению угла между прямой а и плоскостью α на проекционном чертеже. Через точку А, принадлежащую прямой а, проведен перпендикуляр n к плоскости α. Вращением вокруг горизонтали h найдена величина угла γ° между прямыми a и n. Дополняющий угол γ° до 90° является искомым углом ϕ° между прямой а и плоскостью α.
44.4. У гол наклона прямой к плоскости прое кций
Угол наклона прямой к плоскости проекций проецируется без искажения, если прям ая параллельна плоскости проекций (см. рисунки 28 -33).
В случае, когда задана прямая общего положения, следует применить способы преобразования чертежа: замену п лоскостей проекций (рис.100) или вра щение вокруг проецирующей прямой (рис.108).
Напомним, что построением прямоугольного треугольника также можно на йти угол наклона прямой к плоскости проекций (рис.46, 47).
44.5. У гол между плоскостями
Двугранный угол между плоскостями определяют величиной плоского острого угла между прямыми, принадлежащими этим плоскостям и перпендикулярными прям ой пересечения плоскостей.
На рис. 247 показан такой угол φ°. Если вне плоскостей взять произвольную точку А и провести через нее прямые n1 и n2, перпендикулярные заданн ым плоскостям α и β, то величина угла φ° между этими прямыми n 1 и n2 бу дет равна величине угла меж ду плоскостями α и β.
140
