
УчебникНГ_полный
.pdfТочки пересечения плоскости γ с нижним основанием призмы получаем в
пересечении горизонтального следа hoγ с шестиугольником A2'B2'C2'D2'E2'F2 ' в точках
1' и 2'.
Остальные точки пересечения определяем, заключая каждую из граней в горизонтально проецирующую плоскость и находя ее пересечение с заданной плоскостью
γ. Например, грань C1D1C2D2 заключаем в плоскость hoCD. Находим линию пересечения двух плоскостей, заданных следами по точкам пересечения одноименных следов – K(K',K'') и L(L',L''). Фронтальная проекция этой линии пересечения K''L'' пересечёт
фронтальные проекции ребер C1''C2'' и D1''D2'' в точках 3'' и 4''.
Аналогично строим проекции точек 5 и 6, соединяем последовательно все точки на каждой проекции и получаем замкнутую фигуру сечения многогранника плоскостью общего положения.
35.3.Пересечение поверхностей двух многогранников
Вобщем случае два многогранника пересекаются по пространственной замкнутой ломаной линии. В частных случаях эта ломаная линия может распадаться на две и более замкнутые ломаные линии. Вершинами ломаной являются точки пересечения ребер одного многогранника с гранями другого. Стороны ломаной линии представляют собой отрезки прямых, по которым пересекаются грани многогранников. Отсюда следуют, как и
впредыдущем параграфе, два способа построения линии пересечения поверхностей многогранников:
1) Способ ребер — построение вершин ломаной как точек пересечения ребер первого многогранника с гранями второго и ребер второго многогранника с гранями первого. При этом, найденные точки соединяются в определенной последовательности, соблюдая следующее правило: прямыми соединяются лишь те точки, которые принадлежат одной грани.
2) Способ граней — построение сторон ломаной как отрезков прямых попарного пересечения граней данных многогранников.
Выбор способа зависит от свойств пересекающихся многогранников. Построения упрощаются, если вершины и стороны ломаной линии определяются соответственно как точки и прямые пересечения граней общего положения одного многогранника с проецирующими ребрами и гранями другого.
При построении линии пересечения поверхностей двух пирамид, призмы и пирамиды, двух призм в качестве вспомогательных плоскостей можно использовать плоскости общего положения:
1)Если строится линия пересечения поверхностей двух пирамид, то вспомогательные плоскости должны проходить через вершины пирамид;
2)Если строится линия пересечения поверхностей пирамиды и призмы, то вспомогательные плоскости должны проходить через вершину пирамиды параллельно боковым ребрам призмы;
3)Если строится линия пересечения поверхностей двух призм, вспомогательные плоскости должны проходить параллельно боковым ребрам обеих призм.
Указанные плоскости пересекают поверхность пирамиды по прямым, проходящим через ее вершину, а поверхность призмы — по прямым, параллельным ее ребрам. Это в ряде случаев сокращает объем графических построений и позволяет заранее определить те грани одного многогранника, с которыми пересекаются ребра другого.
Рассмотрим два конкретных примера.
Пример 1. Построить линию пересечения поверхностей четырехгранной призмы и трехгранной пирамиды (см. рис.173) Поскольку грани призмы горизонтально проецирующие плоскости, то, воспользовавшись способом ребер, определяем точки
101

пересечения ребер SA, SB, SC пирамиды с гранями призмы просто: горизонтальные проекции их точек пересечения 1' и 4', 2' и 6', 3' и 7' получаются как пересечение указанных ребер с вырожденными проекциями граней призмы.
Из боковых ребер призмы только ребро N1N2 пересекается с поверхностью пирамиды. Для определения точек 5 и 8 её пересечения с поверхностью пирамиды через
неё проведем горизонтально проецирующую плоскость γ, проходящую через вершину
пирамиды S. Плоскость γ пересекает грани SAB и SAC пирамиды по прямым S10 и S9, которые, пересекаясь с N1N2, определяют недостающие вершины 5 и 8 искомой линии пересечения. Она состоит из двух замкнутых ломаных 1-2-3-1 и 5-6-7-8-5.
рис.173
Пример 2. Построить линию пересечения трехгранной пирамиды SABC с прямоугольной призмой (рис.174).
Поскольку грани призмы профильно проецирующие, воспользуемся способом граней.
Т.к. грани призмы являются и плоскостями уровня, то сначала построим сечение
пирамиды плоскостью γ1 верхней грани призмы, обозначенной следом foγ1. Из полученного треугольного сечения выделяем ломанную 1-2-3-4, расположенную в пределах верхней грани призмы. Строим треугольное сечение пирамиды плоскостью
нижней грани призмы — γ2, обозначенную следом foγ2. Выделяем участки ломанной 5-6-7 и 9-10, расположенные в пределах нижней грани.
Поскольку точки 4 и 5 принадлежат одновременно грани SBC пирамиды и передней грани призмы, на чертеже совпадающей с плоскостью β1 и заданной следом
hoβ1, значит, отрезок 4-5 является линией их пересечения. Аналогично, по отрезку 1-10 пересекаются грань SAB пирамиды и передняя грань призмы. Точки 7 и 9 принадлежат задней грани призмы, но различным граням SAC и SAB пирамиды. Поэтому находим
102
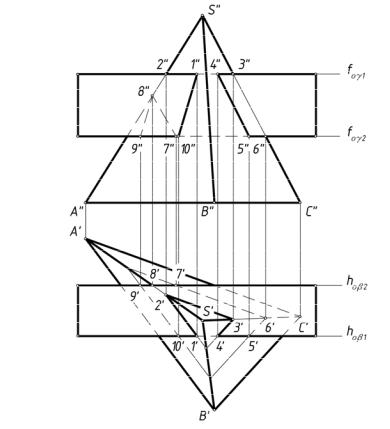
рис. 174
точку 8 пересечения задней грани призмы с ребром SA пирамиды. Горизонтальная проекция 8' точки 8 определяется как точка пересечения S' A' с вырожденной проекцией
задней грани призмы β2, совпадающей со следом hoβ2. Эта задняя грань призмы является фронтальной плоскостью уровня.
Замкнутая пространственная ломаная линия 1-2-3-4-5-6-7-8-9-10-1 представляет собой искомую линию пересечения поверхностей заданных многогранников.
§36. СЕЧЕНИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ ПЛОСКОСТЬЮ
В инженерной деятельности очень часто приходится строить сечение плоскостью поверхностей вращения, которые могут быть частью поверхности детали. Поэтому целесообразно отдельно рассмотреть случаи пересечения плоскостью простейших поверхностей вращения.
Напомним, что поверхностью вращения называется поверхность, образованная вращением некоторой линии вокруг неподвижной прямой. Неподвижная прямая
называется осью вращения поверхности- i, а вращающаяся линия — образующей — g. Задание этих двух линий достаточно для определения поверхности вращения:
геометрической части определителя поверхности Ф(i, g) и алгоритмической части —
вращения g вокруг i.
Сечение поверхности вращения осевой плоскостью называется меридианом поверхности, а осевая плоскость — меридиональной плоскостью. Меридиан, параллельный плоскости проекций, называется главным меридианом. Любое сечение поверхности вращения плоскостью, перпендикулярной оси вращения, будет окружностью. Эти два сечения поверхности вращения очевидны. Рассмотрим некоторые случаи сечения поверхности вращения плоскостью.
103
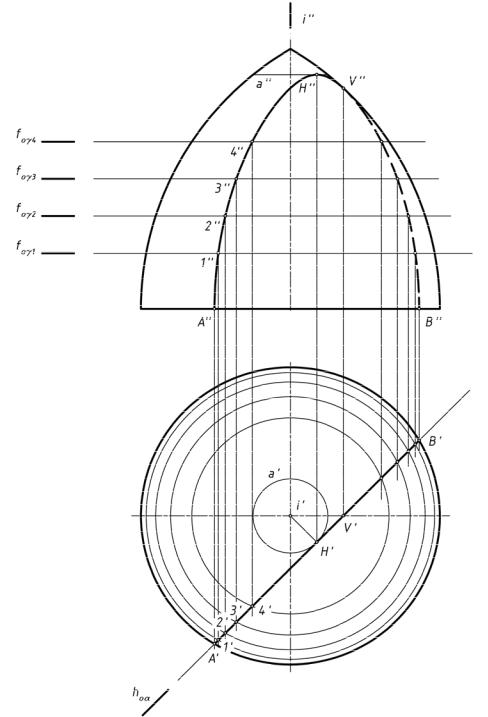
36.1.Сечение поверхности вращения проецирующей плоскостью
Пусть поверхность вращения Ф(i,g) сечется горизонтально проецирующей
плоскостью α, представленной на рис.175 горизонтальным следом hoa. Т.к α — горизонтально проецирующая плоскость, то сечение поверхности плоскостью на
плоскость проекций π1 спроецируется в прямую линию — след hoa.
рис.175
Для построения фронтальной проекции сечения построим проекции каркаса параллелей поверхности, т.е. несколько горизонтальных отрезков, перпендикулярных
проекции оси i" и на равных расстояниях друг от друга. Можно представить, что эти отрезки
104
есть проекции линий пересечения поверхности вращения горизонтальными плоскостями, т.е. параллели этой поверхности. Построим горизонтальные проекции этих параллелей — окружностей. Определяя точки пересечения окружностей-параллелей с горизонтальной
проекцией плоскости α, находим несколько общих точек — 1', 2', 3', …. С помощью линий связи строим фронтальные проекции этих точек и соединяем их плавной кривой. Самой
высокой точкой сечения будет точка H. Она определяется как точка касания параллели a с плоскостью α. Горизонтальная проекция точки H' есть основание перпендикуляра, опущенного из центра i' на hoa. Отрезок i' H' равен радиусу этой параллели.
Точка V есть точка пересечения главного меридиана с плоскостью α и является точкой перехода видимого контура сечения в невидимый.
36.2.Сечение плоскостью общего положения
рис.176
Для построения линии пересечения поверхности вращения β с плоскостью общего положения a необходимо воспользоваться вспомогательными горизонтальными
плоскостями-посредниками, позволяющими легко определить их линии пересечения с a и
β. Надеемся, что не составит труда построить проекции линии пересечения, используя предыдущий опыт рис.172 и рис.175.
105

§37. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ, ОДНА ИЗ КОТО РЫХ ЗАНИМАЕТ ПРОЕЦИРУЮЩЕЕ ПОЛОЖЕНИЕ ОТНОСИТЕЛЬНО ПЛОСКОСТИ ПРОЕКЦИЙ (ЦИЛИ НДРИЧЕСКАЯ ПР ЕЦИРУ ЮЩАЯ)
Кроме плоскости только цилиндрическая поверхность может проецироваться на плоскость пр оекций в линию. На рис.177 представлено пе ресечение поверхности
цили ндра вращения с плоскостью α об щего положения. Плоскость пересекает цили ндрическу ю поверхн ость по эллипсу.
На горизонтальную плоскость проекций эллипс проецируется в окру жность, а на
фро нтальную п лоскость проекций — в эллипс. |
|
|
|
Для нахождения |
фронтальной проекц ии линии пересечения необходимо |
на йти |
|
фро нтальные проекции |
ряда точек, принадлежащих линии пересечения, |
по |
их |
прин адлежности плоскости. |
|
А и |
|
Сначала найдём проекции высшей и низшей точек линии пересечени я (точки |
|||
В). Эти точки расположены в плоскости β, перпендикулярной горизонтальной плоскости проекций и проходящей через ось цилиндрической поверхности (на линии ската плоскости α).
рис. 177
На фронтальной п роекции часть линии пересечения, расположенная на перед ней части цилиндр ической поверхности будет видимой, а на противоположной части — невидимой.
Границей видимости являются точки С и D, расп оложенные в плоско сти главного мери диана цилиндрической поверхности (в плоскости γ). Находим их фронтальные
проекции по принадлежности этих точек плоскости α.
Аналоги чно можно находить фронтальные проекции любых точек, принадлежащ их лини и пересечения.
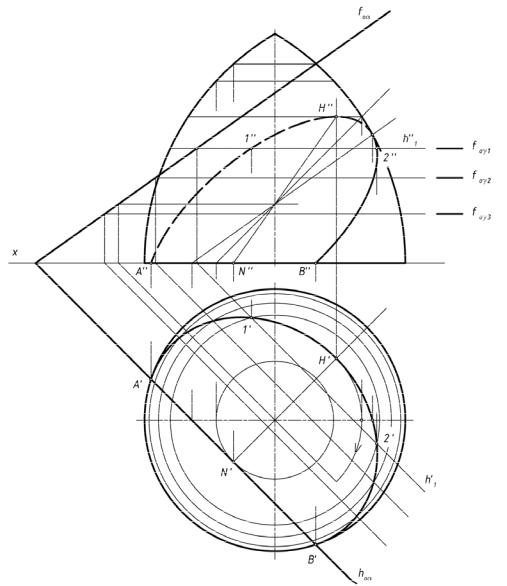
На рис.178 проецирующая плоскость α пересекает все образующ ие цили ндрическо й поверхности. Линия пересечения — эллипс. Его фронтальная проек ция e" — отрезок прямой, совпадающий со следом fоα секущей плоскости. Горизонтальная проекция e' — окружность.
106
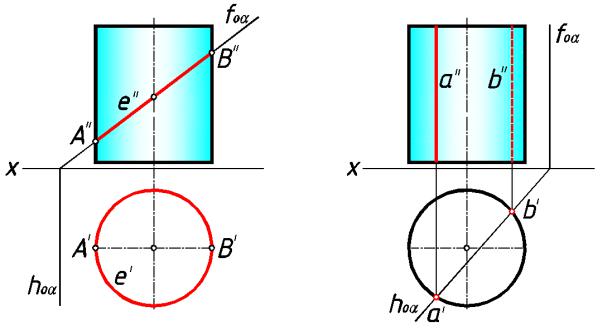
рис.1 78 |
рис.179 |
0
На рис. 179 горизонтально проецирующая плоск ость α параллельна образующим цили ндрическо й поверхности, поэтому пересекает цилиндрическую поверхность по
образующим a и b. Горизонтальные проекции этих образующих принадле жат пересечению горизонтального следа этой плоскости с окр ужностью, в которую проецируется цилиндрическая поверхность на горизонтальную плоскость проекций.
Рассмотрим пересечение проецирующей плоскости с конической поверхностью вращ ения.
На рис унках 180, 181 и 18 2 представлены варианты расположения плоскостей относительно образующ их конич еской поверхностей и лин ий их пересечения с конической поверхность ю.
1. Если плоскость α1 проходит через вершину конической поверхности S и пересекает эту поверхность в единственной точке (в вершине), то всякая параллельная ей
плоскость α2 |
пересечет |
коническ ую поверхность |
по |
эллипсу |
e |
(рис.180 ). В |
частном |
|
случае, когда |
плоскость |
α3 перпендикулярна оси |
кон уса, она |
пересекает |
коническую |
|||
поверхность п о окружности c (по эл липсу с равными осями). |
|
|
|
|
||||
Горизонтальная |
проекция вершины конуса |
S ' является |
одним |
из |
фокусов |
|||
горизонтальной проекци |
и e' эллипса. |
|
|
|
|
|
|
|
Угол наклона секущей плос кости к ос и конуса в этом случае больше угла наклона образующих к оси.
2. Если плоскость β1 проход ит через вершину конической поверхности S и касается поверхности конуса по прямой а, то всякая паралле льная ей п лоскость β2 пересечет
коническую поверхность по параболе p (рис.181).
Горизонтальная проекция вершины конуса S' является фокусом горизонтальн ой проекции p' параболы.
Угол наклона секущей плоскости к оси конуса в этом случае равен углу накл она образующих к оси.
3. Если плоскость γ1 про ходит через вершину конической поверхности S и пересекает поверхность п о двум образующим а и b, то всякая параллельная ей плоскость γ2 пересечет ко ническую поверхность по гиперболе g (рис.182).
107
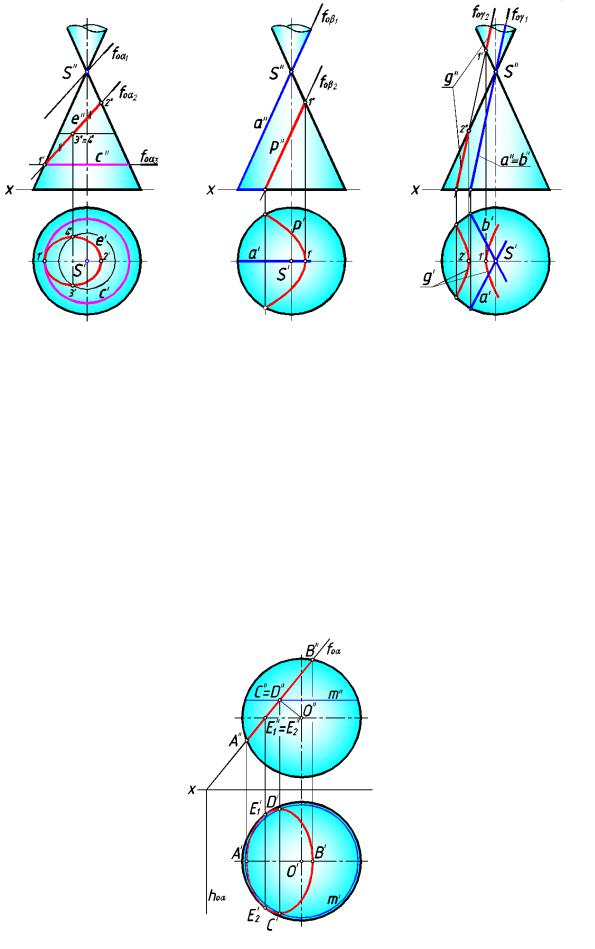
рис. 180 |
рис. 181 |
рис. 182 |
Горизонтальная |
проекция вершины конуса |
S ' является одним из фокусов |
горизонтальной проекци и g' гиперболы.
Угол наклона секущей плоск ости к оси конуса в этом случае меньше угла наклона образующих к оси.
Рассмотрим пересечение фронтально проецирующей плоскости со сферой (рис.18 3). Любая п лоскость пересекает сферу по о кружности.
На фронтальную плоскость проекций окружность проецируется в отрезок А"В" совпадающий с фронтальным следом плоскости и равный диаметру окружности.
На горизонтальну ю плоскость проекций окружность проецируется в эллипс. Большая ось эллипса равна диаметру окружности сечения, т.е. велич ине
фро нтальной проекции этой окружности, а малая ось равна проекции отрезка AB на горизонтальную плоскость проекций.
Точки Е1 и Е2 (граница видимости кривой) распол ожены на экваторе сферы.
Ранее на рис.175 представлено построение линии пересечения пр оецирующ ей плоскости α с поверхностью тора.
рис. 83
108
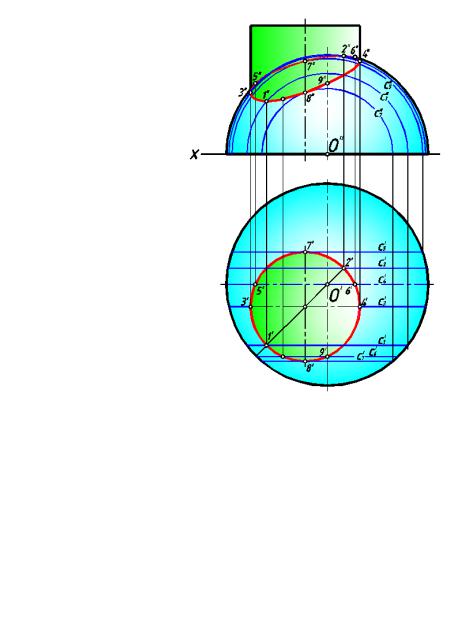
На рис. 184 показано пересеч ение сферы с прямым круговы м цилиндром, который занимает прое цирующее положение относительно горизонтальной плоскости проекций.
Горизонтальная проекция линии пересечения уже известна. Она совпадает с окружностью, в которую проецируется цилиндрическая поверхность на горизонтальную плоскость проекций.
рис. 84
Фронтальную проекцию линии пересечения строят, исходя из её принадлежности
поверхности сферы, с помощью окружностей с1, с2, с3 …с6 и находя на них точки 1, 2, 3…9 , принадлежащие линии пересечения.
Сначала находят п роекции характерных точек линии пересечения. Низшая точка 1
и высшая точ ка 2 принадлежат |
плоскости , проходящей через центр сферы и |
ось |
||
цили ндрическо й поверхности. |
|
|
|
|
Точки |
3 и 4, являющиеся |
границей видимост и |
кривой при проецировании |
на |
фро нтальную |
плоскость проекций, расположены на |
образу ющих цилиндричес кой |
||
поверхности, являющихся очерком этой поверхности на ф ронтальной плоскости проекции. Точки 5 и 6 принадлежат главному меридиану сферы.
Вопросы для самопроверки
¾Какие поверхности могут занима ть проецир ующее положение относительно плоскостей проекций?
¾ Какие |
линии |
являются |
проекциями |
линии |
пересечения |
проецирующ ей |
|
цилиндрической поверхн ости с плоскостью общего положения? |
|||||||
¾ Какие |
линии |
являются |
проекциями |
линии |
пересечения |
проецирующ ей |
|
цилиндрической |
поверхности |
с проецирующей |
плоскостью, произвольно |
||||
наклоненной к оси поверхности? |
|
|
|
|
|||
¾ По каким линиям плоскость, |
параллельна я оси цилиндра, |
пересекает его |
|||||
поверхность? |
|
|
|
|
|
|
|
¾В каких случаях плоскость пересекает коническую поверхность вра щения по двум пересекающимся прямым, поокружности, по эллипсу, по параболе, по гиперболе?
¾По какой линии плоскост ь пересека ет сферу?
¾Какие точки линии пересечения поверхностей относятся к характерным (опорным) точкам?
109
§38. П ЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ОБЩЕГО ПОЛОЖ ЕНИЯ
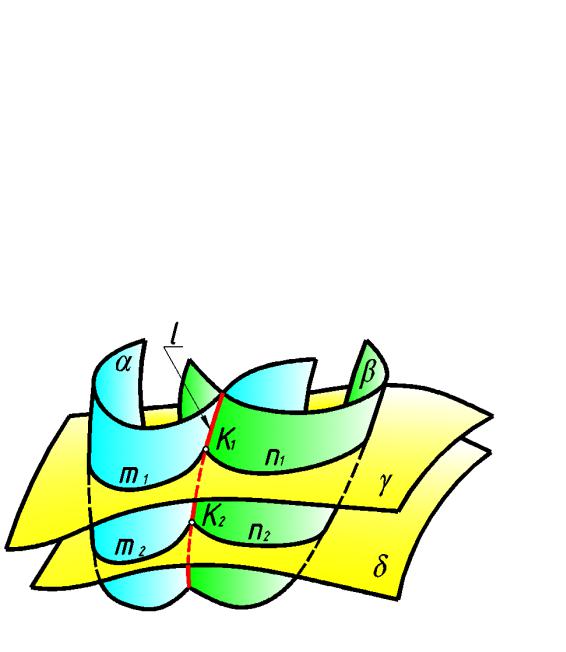
В этом случае применяют особый пр иём для нахождения точек, принадлежащ их лини и пересечения, к оторый называется способом вспомогательн ых секущ их поверхностей (рис.185).
Суть этого способа состоит в том, что для нахождения точки линии пересече ния
поверхностей α и β вводят вспомогательную поверхность γ и определяют линии m1 и n1 пересечения вспомогательной пове рхности с заданными.
На пер есечении п олученных линий расположе на точка K1, принадлежащая как вспомогательной поверхности, так и пересекающимся поверхностям. То есть, эта точка прин адлежат линии пересечения поверхносте й.
Вводя ряд вспомогательных поверхностей, находим достато чное количество точек,
определяющих линию пересечения.
В качестве вспомогательных поверхностей можно использовать как кривые
поверхности, так и плоскости. В последнем с лучае описанный способ называют способом вспомогательных секущих плоскостей.
Вспомогательную поверхность следует |
выбирать таким образом, чтобы |
мож но |
было легко находить линию пересечения её |
с поверхностям и, и чтобы эта |
ли ния |
пересечения проецировалась на плоскость проекций в виде простых линий (прямых и ли окружностей).
рис. 185
38.1. Способ вспомогательных проецирующих плоскостей
На рис.186 представлено построение линии пересечения плоскости общего
положения с поверхностью конуса вращения. В данном случае плоскость α пересекает коническую поверхность по эллипсу, а основание конуса — по отрезку BC.
Сначала найдём высшую точку A лин ии пересечения. Высшая точка принадлеж ит плоскости β, перпендикулярной го ризонтальной плоскости проекций и проходящей через ось конической поверхности перп ендикуляр но плоскости α. Плоскость β пересекает конус по образующей SL, а плоскость α по прямой а. На пересечении этих прямых находится точка A.
Низшими точками являются точки B и C, которы е находятся на горизонтали b, по которой плоскость основания конуса γ пересекает плоскость α.
110
