
УчебникНГ_полный
.pdf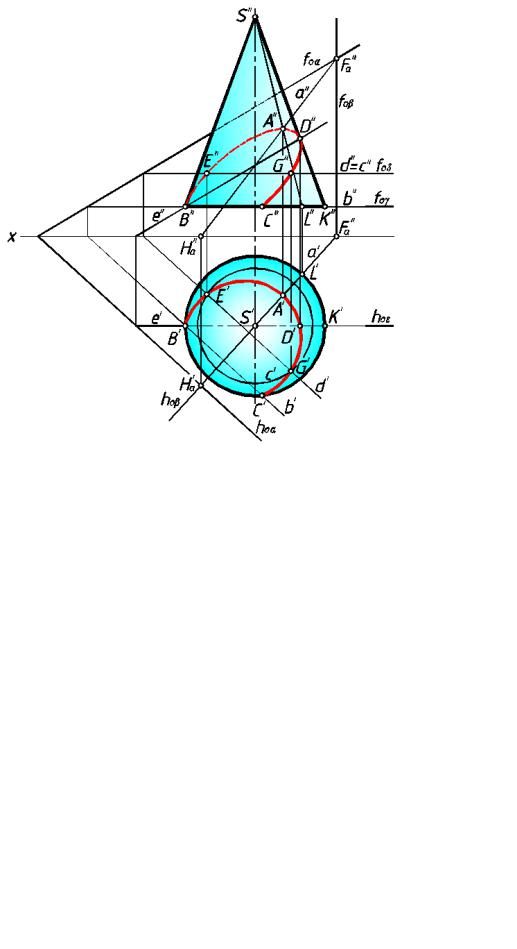
рис. 186
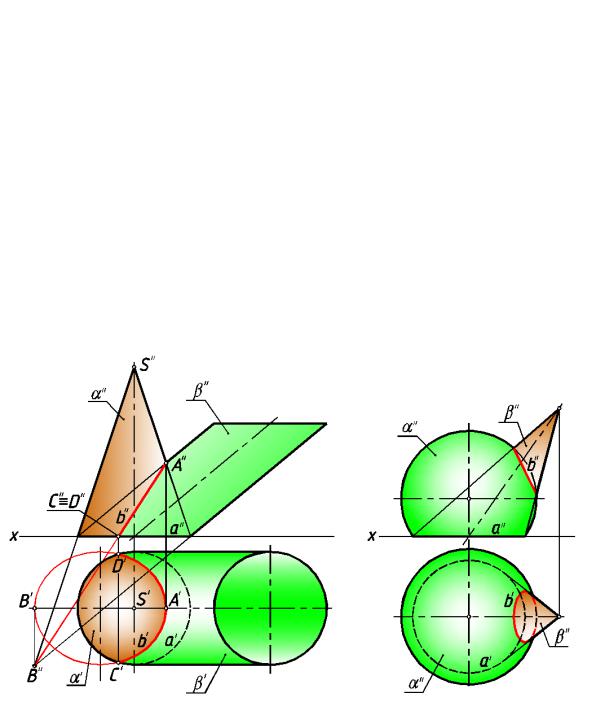
Точка D на очерковой образующей конуса — граница видимости фронтальн ой проекции кривой. Для нахождения этой точки используем проецирующую
вспомогательную плоскость ε, кото рая пересекает конус по образующей SK, а плоскость по фронтали е. Точка их пересечен ия — точка D.
Промежуточные точки линии пересечения легко найти, применяя всп омогательные плоскости пер пендикулярные оси конической поверхности. Эти плоскости пересекаются с
плоскостью α по горизонталям, а с конической поверхн остью по окружностям. Например,
задав вспомогательную секущую плоскость δ, найдем точки E и G. Их проекции находятся на пересечении проекци й окружности с, полученной от пересечения плоскости
δ с конусом, и горизонтали d, полученной от пересечения плоскости δ с плоскостью α. На рис. 187 представлено построение ли нии пересечения сферы с центром в точке О
иконуса вращения, ось которого перпендикулярна горизонтальной плоскости проекций.
Кхарактерным (опорным) точкам лин ии пересечения откосятся точки A, B и C. Точк и A и B являются верхней и нижней точками линии пересечения. Их фронтальные
проекции находятся на пересечении фронтальных проекций главных меридиа нов
заданных поверхностей, которые лежат в плоскости ε, проходящ ей через ось конуса и центр сферы.
Точка С является границей видимости линии пересечения поверхностей на горизонтальной плоскости проекц ий. Поскольку коническая поверхность полностью
видна на горизонтально й проекции, а у сферы только верхняя ч асть до ее экватора e, точка С должна лежать на экваторе сферы. Для нахождения прое кций точки С заключим
экватор е в п лоскость α и построим проекции параллели с, по которой эта плоскость
пересечет поверхность конуса. На пересече нии проекций экватора е и параллели с получим проекции двух точек С1 и С2, в которых линия пересечения изменяет видимость.
111
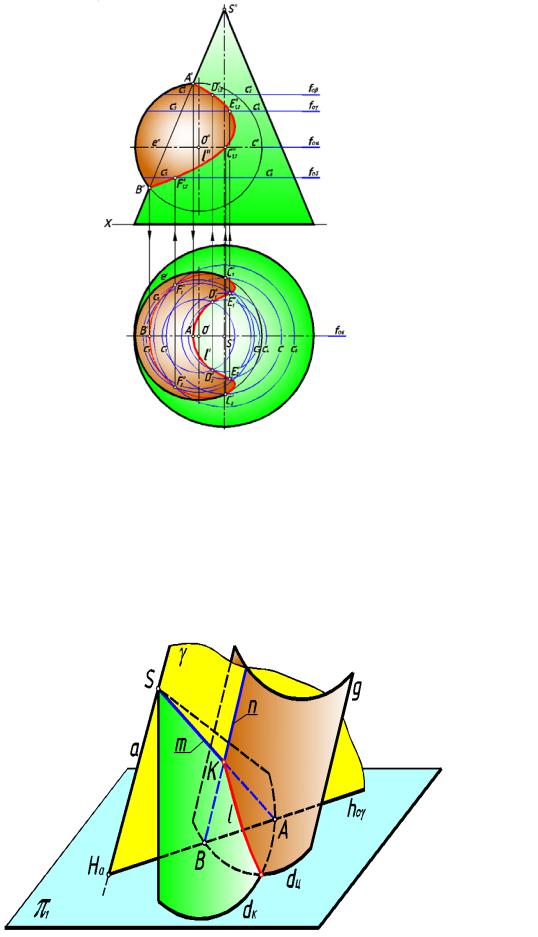
рис. 187
Промежуточные точки линии пересечения находим, вводя ряд п араллельных
горизонтальных секущи х плоскостей: β, |
γ, δ. Каждая из этих плоскостей пересекает |
|
заданные поверхности по окружностям (параллелям) с1 , с2, |
с3, с4, с5, с6, на пересечении |
|
которых находятся искомые точки D1, D2, E1, E2, F1, F2. |
|
|
В заключение заметим: |
легко решена |
способом вспомогательных |
1) данная задача может быть |
||
концентрических сфер (см. §33), |
|
|
2)фронтальнаяпроекцияпостроеннойлиниипересеченияявляетсяпараболой (см.§37 ).
38.2.Сп особ вспом огательных плоскостей общего положения
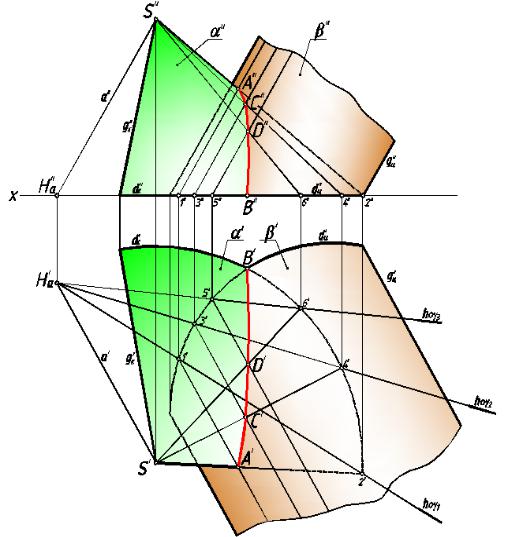
рис. 188
112
При по строении линии |
пересечения линейчатых поверхностей рационал ьно |
использовать вспомогательные |
секущие плоскости общего положения, которые |
пересекают заданные поверхности по прямым линиям — образующ им этих поверхностей. Пересечение конической и цилиндрической поверхностей общего вида показано на
рис. 188.
Для того, чтобы вспомогательная плоскость пересекала цилиндрическую поверхность по прямой (образующей), она должна быть параллельна образующим этой цили ндрическо й поверхности. Дл я того, чтобы плоскость пересекала коническую поверхность по прямой (образующей), она должна прох одить через вершину коническ ой поверхности.
Следовательно, если мы п роведём прямую а через вершину S коническ ой
поверхности параллельно образую щим g цилиндрической поверхн ости, то все плоскости, содержащие эту прямую, будут пересекать обе поверхности по прямым (образующим).
Для построения образующих через то ку Hа пер есечения прямой а с плоскостью π1, на которой находятся направляющие dк и dц задан ных повер хностей, проводим след hоγ вспомогательной плоскости γ. Через точки А и В пер есечения следа с направляющими
поверхностей проводим образующие m и n соответствующих поверхностей. Точка K пересечения образующих является общей точкой поверхностей, т.е. принадлежит линии их пересечения l.
Решение этой задачи в проекциях представлено на рис.189.
рис. 189
113
Рассмотрим построение точек, принадлежащей линии пересечения заданных поверхностей.
При нах ождении образующ их, по которым вспомогательная плоскость пересекает заданные цил индричес кую и коническую поверхности, необходимо определить пересечение вспомогательной плоскости с направляющими заданных поверхностей.
Вспомогательную плоскость задаём прямой а и |
горизо нтальным |
следом |
h оγ1, |
|
который пересекает направляющую цилиндрическую |
поверхность в |
точке |
1, а |
|
направляющую |
конической поверхности точке 2. Через эти точки пройдут образующие, |
|||
по которым |
вспомогательная плоскость пересекает |
заданн ые поверхности. |
На |
|
пересечении этих образу ющих получаем точку А, при надлежащую линии пересече ния заданных поверхностей.
Для построения следующей точки проводим след hоγ2 второй вспомогательн ой плоскости. Через точки 3 и 4 пересечения этого следа с направляю щими цил индрическ ой
и конической |
поверхностей |
проводим об разующие |
этих |
п оверхностей |
и на их |
пересечении |
получаем точку |
С , принадлежащую |
линии |
пересечени я |
заданных |
поверхностей.
Повтор яем описанные действия для получения требуемого количества точек.
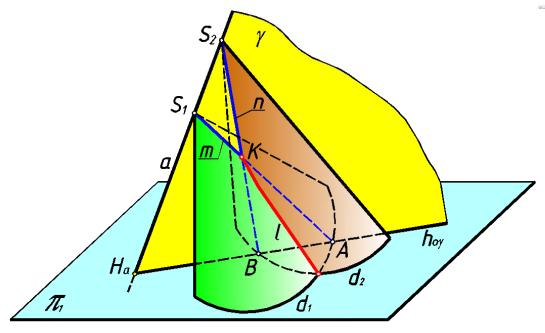
На рис.190 представлено нахождение одной из точек ли нии пересечения двух конических поверхностей .
рис. 190
Для того, чтобы в спомогательная плоскость пересекала к оническую поверхность по прямой (образующей), она до лжна проходить через вершину этой поверхности.
След овательно, если мы проведём прямую а через вершины S1 и S2 заданных коническ их поверхностей, то любая плоскость, проходящая че рез эту прямую, пересечет обе поверхности по прямым линиям (образующим этих поверхностей).
Для построения образующих через то чку Hа пе ресечения прямой а с плоскостью π1, на которой находятс я направляющие d1 и d2 задан ных повер хностей, проводим след hоγ вспомогательной плоскости γ. Через точки А и В пересечения следа вспомогательн ой
плоскости с направляющими |
поверхностей проводим образующие m |
и n |
соответствующ их поверхностей. |
Точка K пересечен ия образующих является |
общ ей |
точкой поверхностей, т.е. принадлежит линии их пересечения l. |
|
|
|
|
114 |
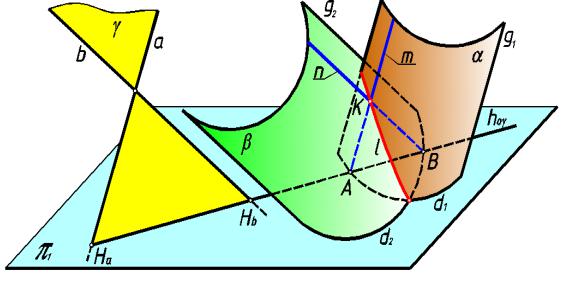
Рассмотрим построение одной из точек линии пересечения двух цил индрическ их поверхностей α и β с образующим и g1 и g2, направляющие котор ых d1 и d2 расположены
на плоскости проекций π1 ( рис.191 ).
Для того, чтобы плоскость пересекала цилиндрическую поверхность по прям ой лини и, она должна быть параллельн а образующим этой поверхности. Следовательно, е сли
задать плоскость γ двумя пересекающимися прямыми a и b, где a||g1 и b||g2, то такая плоскость пересечет обе цилиндрические пов ерхности по прямы м линиям (образующим этих поверхностей).
рис. 191
Горизонтальный |
след hоγ плоскости γ, проходящий через горизонтальные следы |
||
Hа и Hb прям ых a и b, |
пересекает направляющие заданных поверхностей в точках A и B. |
||
Через эти точки |
проход ят образующие m и n, по |
которым плоскость γ пересекает |
|
цили ндрически е |
поверхности. Точка K, в которой |
пересекаю тся прямые m и n, |
|
прин адлежит обеим цилиндрическим поверхностям, а значит, и линии их пересечения l. Проводя следы вспомогательных плоскостей параллельно следу hоγ можно на йти
необходимое количество точек для построения линии l.
Вопросы для самопроверки
¾ В чем суть способа вспомогательных секущих поверхностей, п рименяемого при построен ии линии пересечения поверхностей?
¾ В каких случаях в качестве вспомогательных поверхностей используют плоскости об щего полож ения?
¾ Как следует выбирать вспомогательные плоскости при построении ли нии пересечения коническо й и цилиндрической, двух конических, двух цилиндрических поверхностей общего вида?
38.3.Способ концентр ических секущих сфер
В нек оторых случаях при построении линии пересечения поверхностей целесообразно в качестве вспомогательных поверхностей использовать не плоскости, а сферы. Их п рименение основан о на свойстве соосных поверхностей враще ния
115
пересекаться по окружн |
остям. Соосными называются поверхности вращения, имеющ ие |
|||
общую ось (рис.192, 19 |
3). Отсюда следует, что сфера с центро м на оси поверхности |
|||
вращ ения пересекает эту поверхность по окружностям. |
|
|
|
|
Различают два |
способа: способ концентрических |
секущих |
сфер и |
спо соб |
эксцентрических секущих сфер. |
|
|
|
|
Концентрическими секущими сферами называются |
сферы, |
имею щие |
общий |
|
центр. |
|
|
|
|
Способ применяют при одновременном соблюдении трех условий:
1.Обе пересекаю щиеся поверхности — поверхно сти вращения.
2.Оси поверхностей пересек аются.
3.Оси параллельны одной из плоскостей проекций.
На рис.192 демонстрируется применение способа концентрических сфер при построении линии пересечения поверхности тора и конической поверхности вращения. Все изложенн ые выше ус ловия применения способа соблюдаются.
За центр вспомога тельных сфер прини маем точку О, в которой пересекаются оси поверхностей.
рис. 192
При решении данной задачи необходимо определить величины радиусов сфер, введение которых даёт возмож ность п олучения точек, принадлеж ащих линии пересечения заданных поверхностей. Максимальный радиус сферы равен наибольшему
расстоянию от |
выбранн ого |
цент ра |
вспомогательных |
сфер |
(точки |
пересечения осей |
||
заданных поверхностей) до |
точек |
А и |
В (точек |
пересечения очерков |
заданных |
|||
поверхностей). |
Минимальный радиус |
вспомогательной |
с феры |
равен |
ради усу |
|||
наибольшей из двух сфер, вписанных в заданные поверхности. В нашем примере это радиус сферы, вписанно й в тор.
116
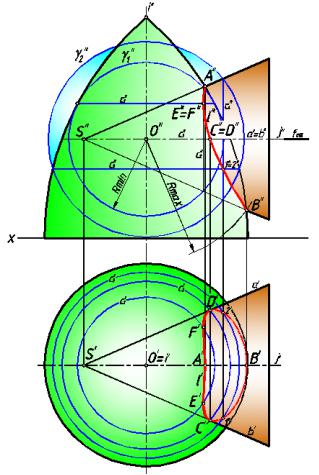
Точки, принадлежащие линии пересечения поверхностей находим следующим образом. Минимальная сфера γ1 касается поверхности тора по окружности с1 и пересекает поверхность конуса по окружности с2. Обе окружности на фронтальную
плоскость проецируются в виде отрезков прямых с"1 и с"2. Так как окружности находятся на общей сфере, они пересекаются в точках E и F. Горизонтальные проекции
этих точек находим на горизонтальной проекции окружности с1. Точки E и F — ближайшие к оси тора.
Следующая вспомогательная сфера γ2 пересекает заданные поверхности по
окружностям с"3 и с"4, которые проецируются на фронтальную плоскость отрезками. На пересечении этих окружностей находим точки 1 и 2. Горизонтальные проекции этих
точек находим на горизонтальной проекции окружности с2.
Продолжая построения по изложенной схеме, находим необходимое количество
точек, которые затем соединяем плавной кривой линией l.
Характерные точки C и D, определяющие границы видимости кривой на горизонтальной плоскости проекций, находим с помощью вспомогательной
секущей плоскости α, которая пересекает тор по окружности с5, а конус по образующим а и b.
38.4. Способ эксцентрических секущих сфер
Эксцентрическими называются сферы с несовпадающими центрами. Способ применяют при одновременном соблюдении трех условий:
1.Одна из пересекающихся поверхностей — поверхность вращения, а втораяповерхность с круговыми сечениями (трубчатая или циклическая).
2.Поверхности имеют общую плоскость симметрии.
3.Плоскость симметрии параллельна одной из плоскостей проекций.
Одним из оснований применения данного способа является то, что одна и та же окружность может принадлежать бесчисленному множеству сфер различного радиуса, центры которых находятся на перпендикуляре к плоскости окружности, проведенном через центр этой окружности.
На рис.194 представлено построение линии пересечения конической и торовой поверхности (кольца). Тор в данном примере используется как трубчатая поверхность, т.е. поверхность с круговыми сечениями в меридиональных плоскостях.
К опорным точкам линии пересечения относятся высшая и низшая точки A и B, определяемые пересечением фронтальных очерков поверхностей, и точки D на границе видимости горизонтальной проекции кривой пересечения поверхностей, которую можно найти только после построения всей кривой.
Для нахождения произвольной точки, принадлежащей линии пересечения указанных поверхностей, на поверхности тора выбираем окружность с1, принадлежащую меридиональной плоскости µ1. На фронтальную плоскость проекций окружность с1 проецируется в отрезок 1"2". Все центры сфер, которые можно провести
через эту окружность, расположены на прямой n1, перпендикулярной плоскости этой окружности и проходящей через её центр С1. Точку О1 пересечения этой прямой с осью
конуса i выбираем за центр вспомогательной сферы и проводим эту сферу γ1 через
окружность с1 на торе. Выбранная сфера пересекает конус по окружности с2, которая проецируется на плоскость проекций в отрезок 3"4". Точки пересечения двух окружностей задают точку K, принадлежащую линии пересечения поверхностей.
Горизонтальные проекции точек находим на параллелях с7 торовой поверхности. Остальные точки кривой находим в той же последовательности.
117
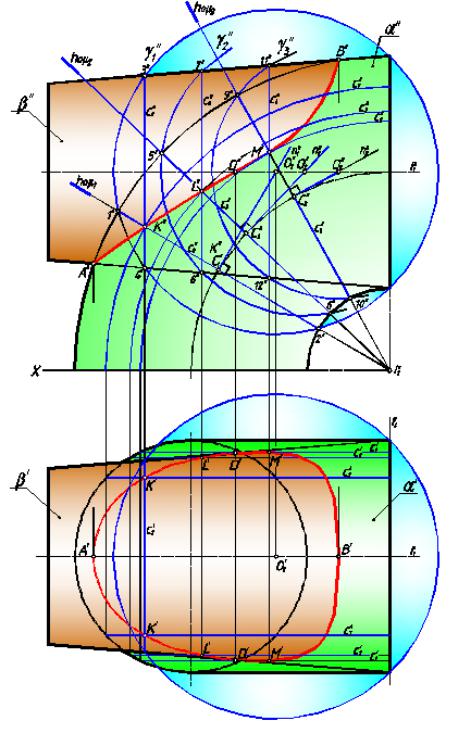
рис. 93
Вопросы для самопроверки
¾В каком случае использу ют концентрические секущие сферы?
¾Где находятся центры вспомогательных секущих сфер?
¾Чему равен радиус наименьшей и наибольшей из применяемых сфер?
¾Опишите последовательность действий для построени я одной из точек ли нии пересечения в способе концентрических секущ их сфер.
¾В каком случае использу ют эксцен трические секущие с феры?
¾Опишите последовательность действий для построени я одной из точек ли нии пересечения в способе эксцентрических секущ их сфер.
118
§39. ЧАСТНЫЕ СЛУ ЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОС ТЕЙ ВТОРОГО ПОРЯДКА
В обще м случае кривые поверхности пересекаются по сложным пространственным кривым линиям. В частн ых случаях рассмотрим линии п ересечения поверхн остей второго порядка [8].
Основная теорем а алгебры применительно к пересечению поверхностей фор мулируется так: две алгебраические поверхности порядков n и m пересекаются по
пространственной кривой порядка n*m.
Следствие из этой теоремы: две поверхности вт орого порядка пересекаются по
пространственной кривой четвертого порядка. |
|
|
И |
ещё одно следствие из основной теоремы: если две |
поверхности второго |
порядка |
имеет общую плоскость симметрии, то линия |
их пересечения при |
пря моугольно м проецировании проецируется на эту плоскость или ей параллельную в кривую второго порядка.
При реш ении прикладных задач встречаются случ аи, когда линии пересечения двух поверхностей распадаются на две и ли более составляю щие. При этом, возможны случаи, когда две или более составляющих совпадают, что ведет к касанию этих составляющих. Рассмотрим некоторые из этих случаев, имея в виду, что ли ния пересечения двух поверхностей второго по рядка в случае их частичного взаимного расположения мо жет
распадаться в таких вариантах: |
|
|
а) |
4=1+3; |
|
б) |
4=1+1+2; |
|
в) |
4=1+1+1+1; |
|
г) |
4=2+2. |
|
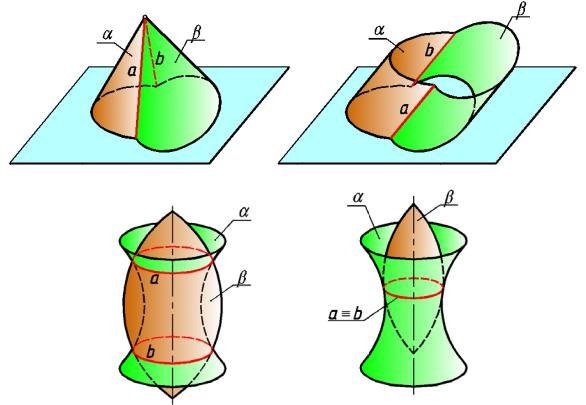
На |
рис.194 показано, что |
две конические поверхности с общей вершин ой |
пересекаются по прямым линиям, |
образующим этих поверхностей. На рис. 195 показаны |
|
два пересекающихся цилиндра с параллельными образующими. Их линии пересечения — общие образую щие.
рис.194 |
рис.195 |
рис.196 |
рис.197 |
119
Две соосных поверхности вращения (рис.196) пересекаются по общим параллелям (окружностям, плоскости которы х перпендикулярн ы оси вращения). Если такие поверхности касаются д руг друга (рис.197), то линия и х касания — окружность (общ ая параллель).
В общем случае |
две поверхности второго |
порядка пересекаются по |
пространственной кривой четвертого порядка, так |
называемой биквадратной |
|
кривой. |
|
|
В частном случае |
эта кривая может распадаться на крив ые меньшего порядка. |
|
Сумма порядков линий, на которы е распадается линия пересечения, должно равняться четырем, т.е. четыре пря мые, две кривые второго порядка и т.д.
Ниже представлены без доказательства несколько теорем относящихся к случаям распадения кр ивой четвертого порядка на линии меньшего порядка.
Теорема 1. Если две поверхности второго порядка пересекаются по одной плоск ой кривой, то они пересека ются и по второй кривой, которая так же является плоской. Этот
случай представлен на рис.198. |
|
|
|
|
|
|
|
Поверхности конуса вращения α и |
эллиптического цилиндра |
β пересекаются |
|||||
по окружности |
а основания конуса (плоская |
кривая). |
Следовател ьно, они пересекаются |
||||
и по второй |
плоской кривой α, проходящей |
через точки А |
и |
В, являющиеся |
|||
пересечением |
очерковых образу ющих заданных |
поверхносте й. |
В |
данн ом |
примере |
||
кривая b — эллипс. |
|
α, то, очевидно, |
|
|
|||
Если о дной из поверхностей является сфера |
второй |
плоск ой |
|||||
лини ей пересечения b будет окружность (рис.199). Эту теорему часто ис пользуют для нахождения круговых се чений на эл липтических поверхностях.
рис. 198 |
рис. 199 |
Теорема 2 (о двойном прикосновении). Если две п оверхности второго порядка α и β име ют две точки прикосновения A и B, то линия их пересечен ия распадается на две плоские кривы е второго порядка а и b, плоскости которых проходят через прям ую, соединяющую точки прикосновения (касания) A и B.
На рис. 200 построена линия пересечения поверхности эллиптического цилиндра и конической поверхности вращения. Точки прикосновения — A и B, линии пересечения а и b — эллипсы. Плоскости кривых а и b пересекаются п о прямой АB.
120
