3. Формула Ньютона (правило трех восьмых)

Более высокую точность вычисления обеспечивает интерполирование подынтегральной функции полиномом третьей степени. В результате получают формулу Ньютона (правило трех восьмых):

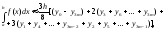
где 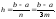Схема алгоритма численного интегрирования по правилу трех восьмых показана на рис. 5.7 Практическое применение нашли также четвертая, пятая и шестая формулы Ньютона-Котеса, однако их использование приводит к более громоздким схемам.

Рис. 5.7 Алгоритм вычисления определенного

интеграла по формуле Ньютона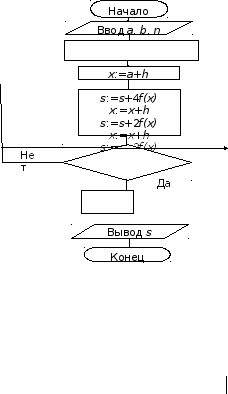

Рассмотренные выше циклические структуры характеризуются одной общей особенностью – во всех рассмотренных примерах заранее можно определить число повторений тела цикла. Задачи, где число повторений заранее неопределенно, приводят к так называемым циклам с неизвестным (до начала цикла) числом повторений.

Пусть, например, надо определить интервал (a, b), внутри которого функция y=f(x) пересекает ось абсцисс (внутри этого интервала функция f(x) обращается в ноль, т. е. f(x)=0). На рис. 5.8 показано возможное решение поставленной задачи в форме соответствующего графика. Первоначально можно предположить, что искомый интервал может иметь границы a=x₀ и b=x₀+h_x. Если в указанном интервале нет искомой точки, то искать ее следует в следующем интервале (a+h_x , b+h_x). Последовательный анализ интервалов продолжается до тех пор, пока не будет достигнут искомый результат. Необходимое условие того, что функция y=f(x) пересекает ось абсцисс, может быть записано в следующем виде: y_a·y_b<0, где y_a = f(a); y_b = f(b).

На рис. 5.9 приведена схема алгоритма нахождения интервала (a, b), с использованием оператора цикла с предусловием.

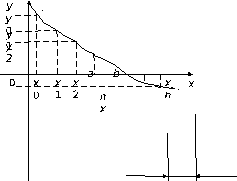
Рис. 5.8 Нахождение интервала, внутри

которого функция пересекает ось абсцисс

Условие продолжения цикла определено с помощью логической переменной v. Значение переменной v формируется из двух условий. С одной стороны выход из цикла возможен в тех случаях, когда найден искомый интервал (a, b), т. е. выполняется условие f(a)f(b)<0. С другой стороны, точка пересечения с осью абсцисс может отсутствовать, тогда выход из цикла осуществляется в результате достижения граничной (конечной) точки x_n. Объединенное условие продолжения цикла

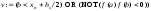
2. Алгоритм вычисления суммы бесконечного ряда

Характерным примером итерационных циклов является задача вычисления суммы бесконечного ряда:

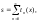
где t_n(x) – слагаемое, зависящее от параметра x (в общем случае) и номера n. Вычисляемая последовательность

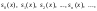
где 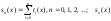– частная сумма.

Для контроля погрешности можно использовать последовательность

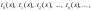
где t_n(x) = s_n(x) – s_n-1(x) – слагаемые ряда n.

.

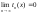Условие выхода из итерационного цикла (справедливо при знакопеременном ряде {t_n(x)}):

| t_n ( x ) | <  .

Алгоритм вычисления бесконечной суммы является модификацией одного из алгоритмов вычисления конечной суммы. Если применение рекуррентных формул нецелесообразно, то вычисления будут наиболее эффективными, если каждое слагаемое определять по общей формуле и полученные значения накапливать в некоторой переменной. Общий вид схемы алгоритма, реализующего вычисление бесконечной суммы с погрешностью  с помощью цикла с предусловием, показан на рис. 5.10, а.

Если для вычисления слагаемых используются рекуррентные соотношения

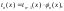
то общая схема итерационного алгоритма для вычисления бесконечной суммы показана на рис. 5.10, б.

Например, тригонометрическая функция sin(x) может быть представлена в виде бесконечной суммы

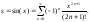
В данном случае

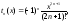
тогда

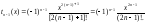
Теперь можно определить

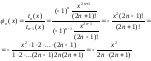
Начальное значение слагаемого находим по формуле