2. Формулы Ньютона-Котеса

Если подынтегральную функцию заменить каким-либо интерполяционным многочленом, то получим квадратурные формулы вида:

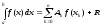
где х_к – выбранные узлы интерполяции; A_k – коэффициенты, которые зависят от выбранных узлов, но не зависят от вида функции f(x); R – остаточный член, определяющий максимальную ошибку при использовании квадратурной формулы; k=0, 1, …, n.

Разбивая отрезок интегрирования [a, b] на n равных частей системой точек

x_k = x₀+kh; k=0, 1, …, n; x₀=a; x_n=b

и вычисляя подынтегральную функцию в полученных узлах

y_k=f(x); k=0, 1, …, n,

получают квадратурные формулы для равноотстоящих узлов. Эти формулы называют формулами Ньютона-Котеса. Наиболее удобны при численном интегрировании интерполяционные многочлены невысоких порядков, при использовании которых получают достаточно простые составные формулы.

1. Формула трапеций.

Формула трапеций получается в случае использования интерполяционного многочлена 1-го порядка:

Остаточный член имеет вид: Использование формулы трапеций при вычислении определенного интеграла приводит к ошибк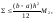егде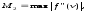

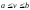
Для нахождения приближенного значения определенного интеграла по формуле трапеций можно использовать алгоритм, схема которого представлена на рис. 5.5.

Ошибка ограничения для метода трапеций больше, нежели чем для других формул Ньютона-Котеса, но его привлекательность заключается в простой реализации. Кроме того, незначительное усложнение алгоритма позволяет существенно снизить погрешность вычислений, поэтому формула трапеций достаточно часто используется (в сочетании с другими формулами).

Например, в случае аппроксимации подынтегральной функции интерполяционным многочленом Эрмита получают формулу Эйлера:

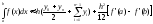
Остаточный член этой формулы свидетельствует о том, что небольшая добавка к формуле трапеций существенно повышает ее точность.

В последней формуле значения производных можно заменить двусторонними разностями

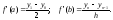
В результате формула Эйлера превращается в формулу Грегори, но общий порядок точности понизится с четвертого до третьего.

2. Формула парабол (Симпсона)

Используя интерполяционный многочлен 2-го порядка (параболу) получают формулу численного интегрирования – формулу Симпсона:

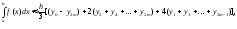
где

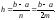
Рис. 5.5 Алгоритм вычисления определенного

интеграла по формуле трапеций

На рис. 5.6 показана схема алгоритма, реализующего вычисления по формуле парабол. При реализации формулы число узлов обязательно нечетно, т. е. число участков разбиения интервала интегрирования должно быть четным: n=2m. В алгоритме использован прием, при котором число повторений цикла уменьшается в два раза, т. е. дважды реализуется модификация параметра цикла, что уменьшает время выполнения алгоритма. Метод Симпсона считается одним из наиболее применяемых методов численного интегрирования, обеспечивающим достаточно хорошую точность вычислений.

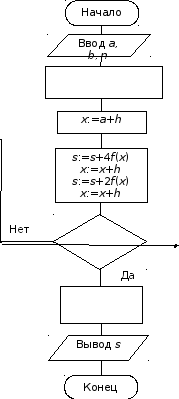
Рис. 5.6 Алгоритм вычисления определенного

интеграла по формуле Симпсона