
- •Движение частиц в одновременно действующих электрическом и магнитном полях
- •Движение частиц в одновременно действующих электрическом и магнитном полях значительной протяжённости
- •Возрастание массы при увеличении скорости
- •Эквивалентность массы и энергии
- •Общие следствия из уравнения движения
- •Форма траектории
- •Движение электрона в поле атомного ядра, описываемое классической теорией
- •Аналоги оптического закона преломления в электрическом и магнитном полях
- •Расчет фокусного расстояния тонкой линзы на основании уравнения движения
- •Электростатическое поле как спектрометр
- •Магнитное поле как спектрометр
- •Каскадный генератор
- •Синхротрон и синхрофазотрон
- •Микротрон
- •Максимальная энергия, достижимая с помощью ускорителей
- •Характеристика диода в высокочастотном поле
- •Фазовая фокусировка
- •Излучающий электрон с точки зрения классической электродинамики
- •Излучение Черенкова
- •Постулаты Бора
- •Спектр излучения
- •Простейшая форма принципа соответствия
- •Модель атома Бора-Зоммерфельда
- •Недостатки теории Бора
- •Аналог волновой оптики
- •Правила вычисления вектора состояния
- •Математические основы квантовой механики
- •Временное изменение ожидаемого значения
- •Роль коммутативности операторов
- •Наиболее важные операторы
- •Система с одним электроном
- •Поведение одноэлектронной системы в магнитном поле
- •Влияние магнитного момента ядра на энергетические состояния атома
- •Понятие микросостояния в квантовой механике
- •Определение распределения, соответствующего состоянию равновесия
- •Связь с макроскопической термодинамикой
- •Классический газ
- •Электронный газ
- •Фотонный газ
- •Природа химической связи
- •Строение твердого тела
- •Распределение потенциальной энергии в металле
- •Зонная теория твердого тела
- •Электроны в периодическом потенциальном поле. Одномерный случай
а) |
б) |
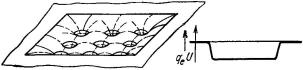
Рис. 116. Распределение среднего потенциала в поле двумерного кристалла (а); упрощенный график изменения потенциальной энергии (б).
электроны движутся в пространстве, свободном от воздействия каких-либо сил, как частицы газа — электронного газа, и только потенциальный барьер на поверхности металла мешает им выйти из металла наружу; ударяясь в поверхность металла, электроны отражаются от нее точно так же, как молекулы газа от стенки сосуда. Их взаимодействие с ионами решетки, однако, важно учитывать и в этом приближении; электроны могут соударяться с ионами и при этом обмениваться с ними энергией.
Вследующем приближении учитывается уже периодичность потенциала. Даже исходя только из периодического изменения потенциальной энергии, можно вывести ценные заключения о возможных состояниях электронов. Мы увидим, что электроны могут находиться только в определенных энергетических зонах.
Наконец, картина будет дополнена, правда, только в общих чертах, рассмотрением взаимодействия между электронами и ионами, что позволит разъяснить приятие электрического сопротивления.
26.4Зонная теория твердого тела
Вдальнейшем следует учитывать, что потенциал внутри тела не постоянен, а соответствует периодичности решетки. Следовательно, вопрос в том, как ведет себя электрон в периодическом потенциальном поле согласно представлениям квантовой механики. В следующем разделе эта задача будет решена количественно. Здесь же мы хотим, прежде всего, добиться качественной характеристики ожидаемых результатов.
Мы начнем с рассмотрения двух различных путей: во-первых, рассмотрим, что происходит при движении свободного электрона в периодическом потенциальном поле; во-вторых, рассматривая электроны, находящиеся в связанном состоянии, исследуем, как изменяется это состояние при объединении в металле множества атомов.
Всоответствии с первым способом рассмотрения проблемы плоская волна, описывающая электрон, должна двигаться в пространстве с периодическим потенциалом. Если эта волна достигнет точки кристалла, в которой потенциал меняется скачкообразно, т.е. встретится с ионом, это приведет к рассеиванию, как и в случае световой волны, которая попадает на маленькую частицу вещества. Из точки скачка потенциала, обусловленного наличием иона, исходят сферические волны по всем направлениям. В связи с тем, что ионы металла находятся в узлах правильной кристаллической решетки, интерференция сферических волн в направлении падения приводит к усилению последних; во всех
211
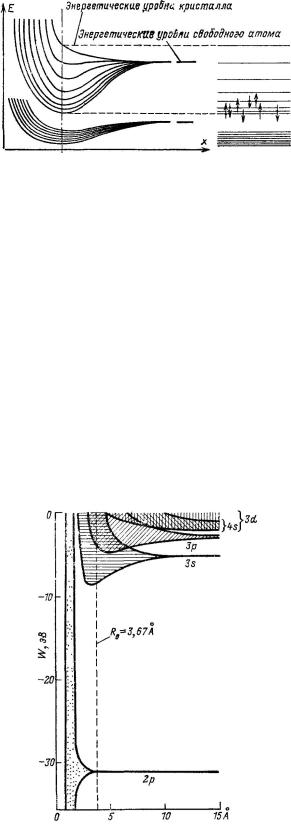
Рис. 117. Расщепление энергетических уровней атома под воздействием полей соседних атомов.
Вправой части рисунка показано положение энергетических уровней в изолированном атоме.
Вположении, соответствующем межатомным расстояниям, равным постоянной решетки a, вся система обладает минимумом потенциальной энергии E. На этом расстоянии возникает, следовательно, стабильная металлическая связь.
других направлениях волны, напротив, ослабляются. В результате плоские волны проходят вещество без рассеивания и, следовательно, без потери интенсивности. Однако из рентгеноструктурного анализа известно, что при определенных углах падения и длинах волн обеспечиваются условия полного отражения — брэгговское отражение. Определение длины волны электрона однозначно задает величину импульса и энергии, так что электроны, обладающие определенной величиной импульса и соответствующей ему величиной энергии, не могут двигаться сквозь металл. Отсюда одновременно следует, что вероятность значений, близких к этим дискретным величинам, тоже очень мала. Таким образом, видно, что энергия электрона не может принимать любое произвольное значение: наряду с разрешенными значениями энергии есть и запрещенные значения или зоны.
Рис. 118. Энергетические зоны натрия.
С помощью второго способа рассмотрения приходят качественно к такому же выводу, т.е. к тем же энергетическим зонам. Рассмотрим сначала два одинаковых атома, бесконечно удаленных друг от друга. Тогда их внешние электроны могут иметь раз-
212

личные энергетические уровни в соответствии с тем, что основному и возбужденным состояниям атома соответствуют различные дискретные значения энергии23, которые при сближении этих атомов изменяются вследствие взаимодействия между атомами, и энергетические уровни расщепляются. Это может быть наглядно прослежено на рис. 117, где энергетические уровни представлены как функция расстояния между атомами для случая с 8 атомами. Поскольку в реальном металле очень много атомов и, кроме того, расщепленные уровни находятся очень близко друг от друга24, мы получаем зоны с почти непрерывным распределением энергии (рис. 118).
Первоначальные дискретные энергетические уровни, расщепляясь, образуют зоны, состоящие из очень большого количества находящихся близко друг от друга энергетических уровней, на каждом из которых согласно принципу Паули могут быть размещены два электрона. Нельзя, однако, обнаружить электрон с величиной энергии, приходящейся на интервал между двумя такими зонами. Этот интервал называется запрещенной зоной. В следующем разделе будет проведено соответствующее количественное рассмотрение. После этого мы еще раз вернемся к качественному рассмотрению зонной структуры.
23Энергетические состояния внешних электронов двух одинаковых атомов будут одними и теми же, так как рассмотрение возбужденных состояний сближающихся атомов не имеет большого смысла, ибо время жизни электрона в таком состоянии мало ( 10 8 с) и если нет внешнего воздействия, то и нет атомов в возбужденном состоянии.
24В энергетической шкале.
213
27 Электроны в периодическом потенциальном поле
27.1Электроны в периодическом потенциальном поле. Одномерный случай
Решение одномерного уравнения Шредингера. Волны Блоха. Количественное исследование соотношений в реальном кристалле, хотя при этом предполагается идеальная (свободная от дефектов) кристаллическая структура, выглядит сложнее. При качественном рассмотрении ожидаемых соотношений одномерной кристаллической модели необходимо, чтобы ионы решетки находились на одной прямой на расстоянии a, соответствующем «периоду решетки». Предположим, что именно вследствие периодичности в точках x; x C a; x C 2a; : : : ; x C na на электрон действует тождественная сила, так что потенциальная энергия Wp .x/, определяющая силы воздействия, периодически изменяется. Предположим дальше, что и вероятности обнаружения электрона в этом месте тождественно равны, т.е.
Wp .x/ D Wp .x C a/I |
.x/ |
.x/ D |
.x C a/ .x C a/: |
(430) |
|||
Здесь .x/ означает решение одномерного уравнения Шредингера: |
|
||||||
d 2 |
|
2m |
W |
Wp .x/ |
|
|
|
|
|
C |
8 |
D 0: |
(431) |
||
|
dx2 |
h2 |
|||||
Исследуем решение с помощью так называемой волны Блоха:
.x/ D Uk .x/ej kx : |
(432) |
Здесь Uk .x/ является периодической функцией:
Uk .x C a/ D Uk .x/: |
(433) |
Правомерность этого подхода (432) можно оправдать двумя способами: во-первых, с помощью этого приема автоматически выполняется уравнение (430), так как
.x |
C |
a/ .x |
C |
a/ |
D |
U |
.x |
C |
a/ej k.xCa/U .x |
C |
a/e j k.xCa/ |
D |
|
|
||||||
|
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
D |
U |
|
.x |
C |
a/U .x |
C |
a/ |
D |
U |
.x/U .x/ |
D |
.x/ .x/: (434) |
|
|
|
|
|
|
|
|
k |
|
k |
|
k |
k |
|
|
||||||
С другой стороны, уравнение (432) обозначает плоскую волну ej kx , амплитуда которой Uk .x/ модулируется с частотой, определяемой периодом решетки, что физически тоже понятно. Что же касается более общего трехмерного случая, то хотелось бы строже обосновать тот факт, что решение должно иметь вид волны Блоха.
Если использовать волну Блоха для решения уравнения Шредингера, получим для функции Uk .x/ следующее дифференциальное уравнение:
d 2Uk .x/ |
|
d Uk .x/ |
|
8 2m |
W |
h2 |
|
|
|
C 2j k |
|
C |
|
|
k2 Wp .x/ Uk .x/ D 0: |
(435) |
|
dx2 |
dx |
h2 |
8 2m |
|||||
Модель Кронига—Пенни. Дальнейшие определения могут быть сделаны только после конкретных предположений относительно зависимости Wp .x/. Модель Кронига—Пен- ни есть модель, отражающая простейшие, но существенные свойства кристаллов. Эта
214

Рис. 119. Модель кристалла Кронига—Пенни и эквивалентная электрическая схема (длинная линия).
кристаллическая модель достаточно просто описывает реальное распределение потенциала (рис. 119): на расстоянии a от иона Wp D 0, затем следует потенциальный барьер шириной b, который повторяется с периодом a C b.
Решение уравнения (435) позволяет тотчас получить значения функции Ux :
|
|
|
|
|
|
|
|
|
|
|
Uk1 D Aej .˛ k/x C Be j .˛Ck/x ; 0 < x < aI |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Uk2 |
|
D C ej .ˇ |
k/x C De j .ˇCk/x ; |
|
|
b < x < 0; |
|
|
|
|
|
|
|
|
|
(436) |
|||||||||||||||||||
причем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˛ D r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2mW |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(437) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˇ D s |
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
.W |
Wp0/: |
|
|
|
|
|
|
|
|
|
|
|
|
|
(438) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Значение констант A, B, C и D получают из следующих четырех граничных усло- |
||||||||||||||||||||||||||||||||||||||||||||
вий25: |
|
|
|
|
|
|
|
|
|
|
|
|
|
ˇxD0 D Uk2 |
ˇxD0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
ˇ |
|
|
|
|
|
|
ˇ |
|
Uk1 |
A C B D C C DI |
|
|
|
|
|
|
|
|
|
|
|
|
(439) |
|||||||||||||||||||
|
|
|
|
D |
|
|
|
|
|
D |
|
|
|
|
ˇ |
|
|
|
|
ˇ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
d Uk |
ˇx |
|
|
d Uk |
ˇx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
D |
|
2 |
|
|
|
; |
|
j .˛ |
k/A j .˛ C k/B D j .ˇ k/C |
|
j .ˇ C k/DI |
(440) |
||||||||||||||||||||||||||||||
|
|
dx |
0 |
|
dx |
|
0 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
ˇxDa D |
|
|
ˇxD b |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
D |
|
|
|
|
C |
|
|
|
|
|
|
|
I |
|
|
|||||||||
|
|
|
|
ˇ |
|
|
|
|
ˇ |
ˇ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uk1 |
ˇ |
|
|
Uk2 |
|
|
; |
|
Ae |
j .˛ k/a |
|
|
|
Be |
j .˛ k/a |
|
C e |
j .ˇ k/b |
|
|
De |
j .ˇ |
C |
k/b |
|
|
(441) |
|||||||||||||||||
|
|
ˇ |
|
|
ˇ |
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
d Uk |
ˇx a D |
|
|
d Uk |
ˇx b |
; j .˛ k/Aej .˛ k/a |
|
j .˛ C k/Be j .˛Ck/a D |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
dx |
|
dx |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
ˇ |
|
|
|
|
|
|
ˇ |
|
|
|
|
|
|
|
D |
j .ˇ |
|
|
k/C e |
|
|
|
|
|
|
j .ˇ |
C |
k/De |
|
|
|
C |
|
|
: |
(442) |
||||||
|
|
|
|
ˇ |
D |
|
|
|
|
|
ˇ |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
ˇ |
|
|
|
|
|
ˇ |
|
|
|
|
|
|
|
|
|
|
|
|
|
j .ˇ k/b |
|
|
|
|
|
|
j .ˇ |
|
k/b |
|
|
|||||||||||
25Постоянные A, B, C , D выбираются таким образом, чтобы функция U.x/ и ее производная d U.x/=dx были непрерывны при x D 0 и x D A и чтобы в силу периодичности U.x/jxDa D U.x/jxD b .
215
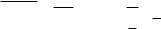
Нетривиальные значения A, B, C , D получают тогда, когда детерминант системы
равен нулю: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ˇ |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
ˇ |
D |
|
j .˛ k/ |
|
|
|
|
C |
k/ |
|
|
|
|
|
j .ˇ k/ |
|
C |
|
0: |
|||||
ˇ |
|
|
j .˛ |
|
|
|
|
|
j .ˇ k/ |
ˇ |
|
||||||||||
ˇ |
|
|
|
C |
|
|
C |
|
|
|
|
|
C |
|
C |
ˇ |
|
|
|||
ˇ |
ej .˛ k/a |
|
|
|
|
|
|
|
|
e j .ˇ k/b |
|
|
ˇ |
|
|
||||||
ˇ |
|
e |
j .˛ Ck/a |
|
|
|
|
|
ej .ˇC k/b |
ˇ |
|
|
|||||||||
ˇ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˇ |
|
|
ˇ |
j .˛ k/ej .˛ k/a |
j .˛ k/e j .˛ k/a |
|
j .ˇ k/e j .ˇ k/b |
j .ˇ k/ej .ˇ k/b |
ˇ |
|
|
|||||||||||||
ˇ |
Более обстоятельное рассмотрение приводит к относительно простому |
выражению |
|||||||||||||||||||
|
ˇ |
|
|
||||||||||||||||||
|
.jˇ/2 |
˛2 |
sh jˇb sin ˛a C ch jˇb cos ˛a D cos k.a C b/: |
|
|
(443) |
|||||||||||||||
|
|
2˛jˇ |
|
|
|
|
|||||||||||||||
|
Для подробного исследования значения W < Wp0 целесообразно ввести величину |
||||||||||||||||||||
|
|
|
|
|
|
jˇ D s |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
8 |
|
.Wp0 |
W / D ˇ0: |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|||||||
|
Отсюда получим уравнение для граничного условия: |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
ˇ2 |
|
|
˛2 |
|
|
|
|
|
|
|
|
|
|
|
|
cos k.a C b/ D |
0 |
|
|
|
sh ˇ0b sin ˛a C ch ˇ0b cos ˛a: |
|
|
|
(444) |
||||||||||
|
|
2˛ˇ0 |
|
|
|
||||||||||||||||
Исходя из представления о бесконечно узком и одновременно бесконечно высоком потенциальном барьере, получим зависимость, описывающую более простые, но весьма существенные особенности. Пусть Wp0 ! 1, b ! 0, однако таким образом, что величина
|
ˇ2ab |
D ı .ˇ ˇ0/ |
Wp0 ! 1 2 |
||
lim |
|
|
b ! 0 |
|
|
остается конечной. В этом случае справедливо s r
ˇb D |
ˇ2ab |
2 |
b D |
||
|
2 |
|
ab |
||
следовательно
ch ˇb cos ˛a !
С другой стороны,
r2 p
ıb ! 0;
a
cos ˛a:
|
ˇ2 ˛2 |
|
ˇ2 |
|
|
|
ˇ |
|
ˇ2b a |
|
|
ı |
|
|||
|
|
sh ˇb ! |
|
sh ˇb ! |
|
|
ˇb ! |
|
|
|
! |
|
|
; |
||
|
2˛ˇ |
2˛ˇ |
|
2˛ |
2˛ a |
˛a |
||||||||||
так что наконец получаем выражение |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
cos ka D ı |
sin ˛a |
C cos ˛a: |
|
|
|
|
|
|
(445) |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
˛a |
|
|
|
|
|
|
||||||||
Это уравнение (445), являющееся исходным для наших дальнейших исследований, выявляет связь между волновым числом k, величиной ˛ и энергией (уравнение (436)), т.е. функцию W D W .k/. Отсюда, если ı D 0; cos ka D cos ˛a и таким образом k D ˛, т.е.
|
h2k2 |
|
2 |
2 |
|
|
p2 |
|||
W D |
|
I |
k D |
|
D |
|
I |
W D |
|
; |
8 2m |
|
h=p |
2m |
|||||||
216

опять получим зависимость между энергией и волновым числом для свободного электрона. Эта зависимость представлена на рис. 120 в виде показанной справа параболы, начерченной прерывистой линией.
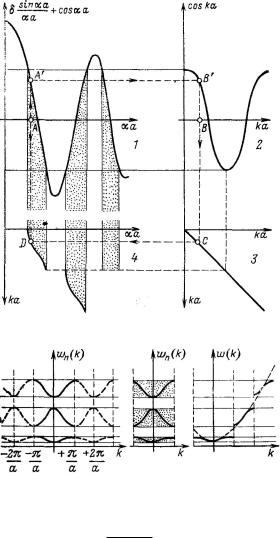
На рис. 120, б приведена зависимость W D W .k/ для общего случая, исходя из уравнения (445), На графике 1 рис 120, а представлена правая часть уравнения (445) в виде функции ˛a. На графике 2 изображена левая часть уравнения (445) в виде функции ka. Очевидно, что действительное значение волнового числа получают только тогда, когда величина правой части уравнения (445) меньше единицы, так как значение cos ka при действительном ka всегда меньше 1. Отсюда следует, что существуют такие значения энергии, для которых нет решения. На рис. 120 коэффициент, определяющий энергию, соответствующую произвольному ˛a, графически представлен таким образом, чтобы спроецировать ординату, относящуюся к ˛a, графика 1 (рис. 120, а, точка А) на график 2, где соответствующее значение k задается абсциссой B. Соответствующую точку графика, представляющую собой конечный результат, получают как точку пересечения D вертикали, исходящей из точки A, с горизонталью, соответствующей величине K. Система координат служит исключительно для облегчения проецирования соответствующей величины ka с помощью прямой, проведенной под углом 45˚.
На рис. 120, б показан такой же график 4, отличающийся от предыдущего тем, что на вертикальной оси вместо ˛a нанесена величина, пропорциональная непосредственно
энергии:
.˛a/2 D 8 2ma2 W: h2
Из уравнения (445) или из рис. 120, а, наглядно демонстрирующего взаимосвязь различных величин, видно, что каждому допустимому значению энергии, которое отличается одно от другого только целочисленным коэффициентом, кратным 2 =a, соответствует бесконечно большое количество значений k. На рис. 120 (левая часть) приведена кривая, показывающая периодическую зависимость W D W .k/ от k. Однако если значение k остается в интервале
|
|
|
|
|
6 k 6 C |
|
; |
a |
a |
||
то получают семейство кривых, представленных на рис. 120. Для установления однозначного соответствия этих параметров индексом обозначают, к какой зоне относится значение энергии соответствующее данному значению k:
W D Wn.k/:
Взаимно-однозначное соответствие может быть достигнуто и тем, что со следующими друг за другом областями изменения величины k будут сопоставлены следующие одна за другой энергетические зоны.
Предварительно заметим, что область изменения значений k: a 6 k 6 C a называют первой зоной Бриллюэна, область 2a 6 k 6 6 k 6 C 2a — второй зоной Бриллюэна и т.д. На рис. 120, б представлены зависимости Wn.k/ в схеме повторяющихся зон, в схеме приведенных зон, в расширенной зонной схеме.
Аналогия с линиями передач. Система допустимых и запрещенных значений энергии очень напоминает чередование полос пропускания и запирания многозвенного фильтра, особенно если учесть, что зависимость энергии от времени определяется выражением
ej ! t D ej 2 t D ej 2 Wh t ; ! $ W:
217
а)
б)
Рис. 120. Определение возможных значений ˛a в модели Кронига—Пенни (а). В качестве ре-
зультата получаем схему 4, где ˛a D a |
8 2 mW |
представлена как функция ka, и схематическое |
|
h2 |
|||
изображение различных возможных зависимостей W |
W .k/ для случаев периодического по- |
||
q |
|
|
|
D
вторения, ограничения и уширення (б).
Действительно, эти явления аналогичны даже в количественном отношении, так что для решения уравнения Шредингера в случае модели Кроннга—Пенни может быть использована теория, описывающая линии передач. Периодически изменяющемуся потенциалу соответствует электрическая цепь с изменяющимся волновым сопротивлением.
Решение дифференциального уравнения, описывающего напряжение, мы ищем в виде, который обеспечивает непрерывность U и d U =dx вплоть до границ рассматриваемой области. В случае волны производная d U =dx непосредственно связана с силой тока I . Требование непрерывности U и d U =dx выражает, следовательно, тот простой и само собой разумеющийся факт, что в непосредственной близости от области поглощения напряжение или сила тока должны существовать как слева, так и справа от этой области.
Для того чтобы обеспечить полную аналогию с уравнением телеграфной линии, вводим с
помощью уравнения |
|
|
|
|
|
d |
D |
j 2 |
W |
I |
|
|
|
|
|||
|
dx |
h |
|||
силу тока I . Она, естественно, является фиктивной. Уравнение Щредингера разделяется вслед-
218

ствие этого на два дифференциальные уравнения первого порядка:
|
d |
D |
|
|
|
W |
I |
|
|||||||
|
|
|
|
|
|
|
j 2 |
|
I |
(446) |
|||||
|
|
dx |
|
h |
|||||||||||
|
|
d U |
D |
|
j 2 LI I |
(447) |
|||||||||
|
|
|
|
|
|
||||||||||
|
|
|
dx |
||||||||||||
dI |
|
|
|
|
|
|
W 2m.W |
Wp0/ |
|
||||||
|
D j 2 |
|
|
|
|
|
|
I |
(448) |
||||||
dx |
h |
|
|
|
W 2 |
|
|||||||||
|
|
|
dI |
D |
|
j 2 C U: |
|
|
(449) |
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
dx |
|
|
|
|||||||||
Для сравнения также записано дифференциальное уравнение для длинной линии. Сразу же видны аналогии между отдельными величинами:
U ! |
; I ! I ; ! |
W |
; L ! 1; C ! |
2m.W Wp0/ |
|
|
|
|
: |
(450) |
|||
h |
W 2 |
|||||
На рис. 119 дана длинная линия, которую можно рассматривать как аналог нашей кристаллической модели. Ее можно также рассматривать как цепь, состоящую из симметричных четырехполюсников. Полоса пропускания и область запирания фильтра, составленные из симметричных элементов, могут быть определены с помощью члена A11 матрицы A. Известные соотношения между входящими в это выражение величинами позволяют записать:
U1 D ch gU2 C Z0 sh gI2I |
(451) |
|||
I1 D |
sh g |
U2 |
C ch gI2: |
(452) |
|
||||
Z0 |
||||
Здесь Z0 обозначает полное волновое сопротивление четырехполюсника и g — коэффициент переноса, следовательно, при е g имеем отношение U2/U1. Если, таким образом, четырехполюсник находится в положении пропускания или запирания, то значения g соответственно являются действительными или мнимыми. В случае идеальной электрической цепи
p p
g D j 2 LC l I Z0 D L=C ;
где L и C обозначают соответственно индуктивность, приходящуюся на единицу длины, и емкость.
Сообразно с этим можно определить значения ch g для элемента, представленного на рис. 121, а. Этот элемент состоит из двух асимметричных четырехполюсников, которые в свою очередь состоят из двух элементов, включенных последовательно (рис. 121). В асимметричном случае имеют место соотношения
U1 |
|
A.1/U2 |
A.1/I2 |
|
|
U1 |
D A.1/ |
U2 |
I |
|||
|
|
|
11 |
|
12 |
|
|
|||||
I |
1 |
DA.1/U |
2 |
CA.1/I |
|
I |
I1 |
I2 |
||||
|
D |
21 |
C 22 |
2I |
|
|
|
|
|
|||
|
|
|
|
|
.1/ .1/ |
|
.1/ .1/ |
D 1: |
|
|
||
|
|
|
|
|
A11 A22 |
|
A12 |
A21 |
|
|
||
Если поменять местами начало и конец упомянутого выше асимметричного четырехполюсника, то матрица A.2/ примет вид:
A.2/ |
|
.1/ |
.1/ |
|
|
A22 |
A12 |
: |
|
|
D |
.1/ |
.1/ |
! |
|
A21 |
A11 |
219
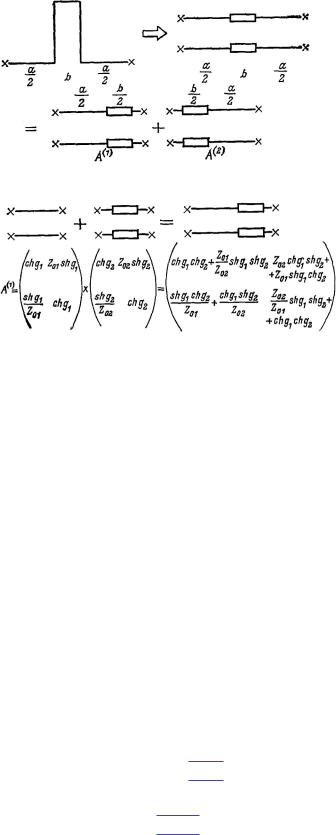
а)
б)
Рис. 121. К определению членов матрицы, описывающих элементы эквивалентной схемы, представленной на рис. 119.
Так как нас интересует только первая компонента получающейся матрицы Ar es , она легко может быть найдена, исходя из правил умножения для матриц:
r es |
.1/ .2/ |
.1/ .2/ |
.1/ .1/ |
.1/ .1/ |
.1/ .1/ |
|
A11 |
D A11 A11 |
C A12 A21 |
D A11 A22 |
C A12 A21 |
D 2A11 A22 |
1: |
В последнем преобразовании использовано соотношение
.1/ .1/ |
.1/ .1/ |
D 1: |
A11 A22 |
A12 A21 |
В результате: умножения, используя дополнительное условие, получаем:
A11r es D 2A11.1/A22.1/ |
1 D |
Z02 |
C |
Z01 |
sh 2g1 sh 2g2 |
C ch 2g1 ch 2g2: |
Z01 |
Z02 |
С другой стороны,
Ar11es D ch gr es :
Следовательно, если принять во внимание соотношения
p
2g1 D j 2 pL1C1 2g2 D j 2 L2C2
gr es D j k.a C b/I p
Z01 D pL1=C1I Z02 D L2=C2;
aI bI
а также использовать величины, соответствующие им, по указанной аналогии, то получим уравнение (444).
220

Кристаллическая решетка конечного размера. До сих пор мы исследовали бесконечную одномерную кристаллическую решетку. Теперь предположим, что задана длина кристалла L, которая имеет конечное значение. Таким образом, мы имеем в целом L=a узлов решетки. Можно предположить, что в случае, когда L=a представляет собой очень большое число, нельзя определить существенные отклонения от решения, характерного для бесконечного кристалла. Аналогия с длинной линией, однако, требует одной оговорки. Длинная линия конечной длины представляет собой колебательную систему. Стационарное состояние возникает только при совершенно определенных частотах и соответственно при совершенно определенных длинах волн, которые хотя и состоят из бесконечного множества членов, однако образуют дискретное множество значений. Применительно к значениям энергетических уровней периодического потенциала это означает, что эти величины не непрерывно изменяются внутри зоны, а могут принимать внутри ее только определенные дискретные значения. Для определения числа и положения этих дискретных величин используем естественные допущения, что на обоих концах кристалла имеют место одинаковые соотношения. В связи с аналогией с длинной линией это означает, что, например, начало и конец линии могут быть разомкнуты или накоротко замкнуты.
Идентичные соотношения для начала и конца кристалла получаются при условии, что уравнение, определяющее энергию, имеет вид:
cos.k 0/ D 1 D cos.k L/:
В этом случае левая часть уравнения (444) в точках x D 0 и x D L, а следовательно, и правая часть имеют идентичные энергетические значения. Условие возникновения этого состояния:
т.е. |
|
|
kL D l 2 ; |
||||
2 |
|
l 2 |
|
||||
k D l |
D |
I l D 1; 2; : : : ; N; |
|||||
|
|
|
|
||||
L |
N a |
||||||
где N обозначает число узлов решетки. Отсюда можно сразу же подсчитать, что k ни в коем случае не может принимать произвольное значение между 0 и 2 =a или=a и C =a, а имеет лишь дискретные значения, определенные вышеприведенным уравнением. Ясно также, что в указанной теперь зоне имеется N различных значений k
исоответственно этому N различных значений энергии W . При очень большом числе атомов решетки два следующие один за другим значения k очень мало различаются, как
исоответствующие значения W , так что практически зона может рассматриваться как континуум.
Подытоживая сказанное, можно заключить следующее: описывая поле твердого тела с помощью периодического потенциала, подразумевают, что допустимые значения энергии составляют зоны, которые отделены друг от друга запрещенными зонами. Хотя разрешенные значения энергии внутри зоны могут практически рассматриваться как непрерывно изменяющиеся, каждая энергетическая зона состоит в действительности из такого же числа дискретных энергетических уровней, которое равно числу атомов, содержащихся в кристалле26.
26Полученный вывод совершенно очевиден. Действительно, согласно принципу Паули в любой квантовой системе, каковой, в частности, является рассматриваемый кристалл, не могут существовать электроны, обладающие одинаковым набором квантовых чисел. Но ведь мы образуем кристалл из N одинаковых атомов. Поэтому каждый из N одинаковых уровней этих атомов, занятый электронами, должен слегка изменить свою первоначальную энергию, что и приведет к образованию зоны, состоящей из дискретных уровней.
221

27.2Электроны в периодическом потенциальном поле. Трехмерный случай
Исследуем теперь соотношения, существующие в реальных трехмерных кристаллах. Согласно уравнению Шредингера в данном случае
~2 |
|
2m 4 .rE/ C Wp .rE/ .rE/ D W .rE/; |
(453) |
причем периодичность потенциальной энергии Wp соответствует периодичности решет-
ки: |
|
|
E |
D |
|
E C |
|
|
|
|
|
|
|
|
R /: |
|
|||||
|
W .r / |
|
Wp .r |
|
|
|||||
|
|
p |
|
|
|
En |
|
|||
При этом |
|
D |
|
E |
C |
E |
C |
E |
|
|
En |
|
|
||||||||
|
n1a1 |
|
n2a2 |
|
|
n3a3 |
(454) |
|||
R |
|
|
|
|
|
|
|
|
|
|
обозначает вектор решетки, aE1, aE2, aE3, являются векторами базиса, характеризующими расположение элементарных ячеек, а n1, n2, n3 — любыми целыми числами (рис. 122).
Для решения уравнения (453) используем теорему Флюге—Блоха, согласно которой
функция, описывающая решение уравнения |
.rE/, обладает следующим свойством: |
|||||
E C |
R |
/ |
D |
kR |
E |
(455) |
|
||||||
.r |
|
ej E En .r /; |
||||
En |
|
|
|
|
|
|
где E означает произвольный вектор. Сразу же ясно, что уравнение этого типа полностью k
соответствует нашим предположениям, сообразно с которыми функция, описывающая вероятность местопребывания электрона, обладает той же периодичностью, что и решетка. Если использовать решение в вышеуказанной форме, то
.r R |
/ |
.r R |
/ |
D |
ej E En |
.r /e |
E En |
.r / |
D |
.r / |
.r /: |
E C En |
|
E C En |
|
kR |
E |
j kR |
E |
E |
E |
||
|
|
|
|
|
|
|
|
|
|
Прежде чем доказать теорему Флюге—Блоха, укажем на существенное следствие этой теоремы, а именно на то, что функция
u.r / |
|
e |
j E E |
.r / |
(456) |
E |
D |
|
kr |
E |
|
|
|
|
имеет ту же периодичность, что и решетка. Если предположить, что теорема Флюге— Блоха справедлива, то
e |
j E EC En |
|
.r R / |
|
e |
E E e |
E En e |
E En |
.r / |
e |
E E |
.r /: |
|
|
k.r R |
/ |
E C |
En |
D |
|
j kr |
j kR |
j kR |
E D |
|
j kr |
E |
|
|
|
|
|
|
|
|
|
|||||
Умножив уравнение (456) на ErE , можно представить решение в следующем виде:
k
j
e
E E
.rE/ D ej kr u.rE/;
причем
E C E D E u.r Rn/ u.r /:
(457)
(458)
Это уравнение называют функцией Блоха или волной Блоха. Она может быть интерпретирована как плоская волна, амплитуда которой периодически модулируется. Непосредственное следствие из теоремы Флюге—Блоха, таким образом, гласит: решение урав-
нения Шредингера в поле периодического потенциала может быть представлено в виде волны Блоха.
222
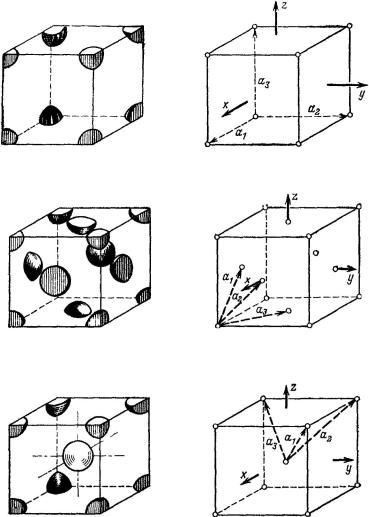
a1 D ai I a2 D aj I a3 D ak
а)
a1 D a2 .k i /I a2 D a2 .j C k/I a3 D a2 .j i /
б)
a1 D a2 .i C j C k/I a2 D a2 . i C j C k/I a3 D a2 . i j C k/
в)
Рис. 122. Три простейших типа решетки и векторы базиса, характеризующие отдельные типы решетки.
а — простая кубическая решетка; б — кубическая гранецентрированная решетка. Такую решетку имеют следующие элементы - Сu, Ag, Аu, Al, Fe. /, Рb, Ni; в — кубическая объемноцентрированная решетка. Сюда относятся Fe.˛/, Li, K, Na, V, Та, Сr, Mo, W.
223
Теперь перейдем к доказательству теорзмы Флюге—Блоха. Введем прежде всего оператор
E |
E C |
. Обратными этому оператору |
|
R |
|
сдвига Rn, который переводит вектор точки r |
в вектор точки r En |
|
являются оператор 4 и инварианты Wp . Таким образом, получим:
@2 |
D |
@2 |
; |
@2 |
D |
|
@2 |
|
|
; |
||||||
|
@x2 |
@.x C Xn/2 |
|
@y2 |
@.y C Yn/2 |
|||||||||||
причем |
|
|
|
|
E |
D |
|
E C |
|
|
|
I |
||||
|
|
|
|
|
|
|
|
R |
||||||||
|
|
|
|
Wp .r / |
|
Wp .r |
|
/ |
||||||||
|
|
|
|
|
E C |
En |
|
|||||||||
|
|
|
|
En D |
|
|
nE C |
n |
|
n E |
||||||
|
|
|
|
R |
|
|
X i |
|
Y j |
|
Z k: |
|||||
Отсюда следует, что |
|
|
Rn.H / D H.Rn |
|
|
|
||||||||||
|
|
|
|
|
/; |
|||||||||||
т.е.
@2 |
D |
@2 |
; |
|
|
@z2 |
@.z C Zn/2 |
||
RnH HRn D 0:
Оператор Гамильтона и оператор сдвига, таким образом, можно менять местами. Это означает, что собственно функции H и Rn идентичны. Поэтому справедливо
|
|
E |
D |
E C |
R |
/ |
D |
C |
|
E |
|
|
|
|
|
|
(459) |
|||||
|
Rn |
.r / |
|
.r |
|
|
n |
.r /; |
|
|
|
|
||||||||||
|
|
|
|
|
En |
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|||
|
E |
|
|
|
|
|
|
|
|
|
|
|
R |
|
. И так как |
|
C |
|
, то, |
|||
где величина Cn не зависит от r , однако может зависеть от |
En |
|
|
RnRm |
|
Rn m |
|
|||||||||||||||
следовательно, CnCm D CnCm. Это уравнение удовлетворяет соотношению |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
kR |
|
|
|
|
|
|
|
|
|
|
|
|
(460) |
||
|
|
|
|
Cn D ej E En : |
|
|
|
|
|
|
|
|
|
|
|
|||||||
k выбрана чисто произвольно, чтобы не получать бесконечно большие величины. |
||||||||||||||||||||||
Величина j E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Принимая во внимание отношение (459), получают: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
.r Rn/ |
|
ej E En |
.r /; |
|
|
k |
.r / |
u |
k |
.r /e E E ; |
|
|
|
|
|
|||||||
|
E |
|
|
kR |
|
|
|
|
|
|
|
|
|
|
j kr |
|
|
|
|
|
||
E C |
|
D |
|
E |
|
|
|
E E D |
|
E |
|
E |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k. |
|
|
|
|
|
т.е, волну Блоха. Частные решения здесь обозначены с помощью индекса E |
|
|
|
|
|
|||||||||||||||||
Теперь установим величину |
k и подставим вышеуказанное решение в уравнение |
|||||||||||||||||||||
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Шредингера (453). Тогда получим следующее дифференциальное уравнение для функ-
E |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ции uk |
.r /: |
2m E |
|
|
4 |
|
|
|
|
m E |
|
C |
|
E |
E E D |
|
E E |
|
|
||||||||
|
|
~2 |
.k2 |
|
|
|
/ |
|
j |
~2 |
kgrad |
|
Wp .r / uk .r / |
|
W uk .r /: |
(461) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
k, как и при краевых условиях |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
При данном E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
E E C |
R / |
D |
u |
E |
|
E I |
grad u |
E |
E C |
R |
/ |
D |
grad u |
E |
E |
I |
(462) |
|||||||
|
|
uk .r |
|
En |
|
|
|
|
k |
|
|
|
|
|
k |
|
En |
|
|
|
|
k |
|
|
|
||
можно получить решение этого дифференциального уравнения только для дискретных значений энергии W :
|
|
|
|
W |
1 |
|
E |
W2. E |
|
|
|
n |
|
E |
|
|
|
|
|
||
|
|
|
|
|
.k/; |
|
|
k/; : : : ; W |
|
.k/ : : : |
|
|
|
|
|||||||
|
|
|
|
|
E |
E |
|
E |
E |
|
: : : ; |
|
E |
E |
: : : |
|
|
|
(463) |
||
|
e |
E |
|
u1k |
.r /; |
u2k |
.r /; |
|
unk |
.r / |
e |
|
|
||||||||
|
u .r /; |
|
|
|
|
ej E E u .r /; : : : ; |
|
E E u .r / : : : |
|||||||||||||
E D |
|
j k r |
E E |
|
|
E D |
|
kr |
|
E E |
|
|
|
|
E D |
|
j kr |
E |
E |
||
1k |
|
|
1k |
|
|
|
2k |
|
|
|
2k |
|
|
|
|
nk |
|
|
nk |
|
|
Теперь исследуем, как величины |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
E |
E |
|
E |
E |
|
|
|
k/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
k .r /; |
uk .r /; |
W . E |
|
|
|
|
|
|||||||
224
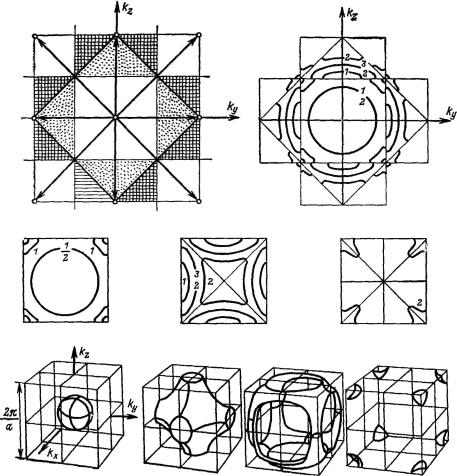
а) |
б) |
в)
г)
Рис. 123. Варианты изображения функции D E в «плоской» и объемной решетке.
W W .k/
а — строение зон Бриллюэна для двумерной простой кубической решетки, средний белый квадрат представляет собой первую зону; часть обозначенная точками, соответствует второй зоне, а
покрытая клетками — третьей; б — схема расширения зон при D E ; в — схема сокращения
W W .k/
зон. Она получена на основании б, однако части второй в третьей зон сдвинуты в первую; г — плоскости постоянной энергии в случае простейшей объемной решетки для случая сокращения
зон, но только для 1 D 1 E .
W W .k/
225

зависят от E (рис. 123). Для того чтобы ответить на этот вопрос, введем понятие об- k
ратной решетки. Элементарные векторы E1, E2, E3, характеризующие обратную решетку, b b b
определим с помощью следующих отношений:
E E D |
|
D |
1; |
i D j: |
bi aj |
2 ıij ; ıij |
|
0; |
i ¤ j I |
Очевидно, что векторы
b |
D |
2 |
aE2 aE3 |
I |
b |
D |
2 |
aE3 aE1 |
I |
b |
D |
2 |
aE1 aE2 |
E1 |
|
a a a |
E2 |
|
a a a |
E3 |
|
a a a |
|||||
|
|
|
E1 E2 E3 |
|
|
|
|
E1 E2 E3 |
|
|
|
|
E1 E2 E3 |
удовлетворяют уравнению (464). Попутно заметим также, что
E E E D .2 /3 b1b2b3 aE1aE2aE3 :
(464)
(465)
(466)
Это уравнение отражает связь между объемами элементарных ячеек нормальной и обратной решеток. На рис. 124 приведены обратные векторы в случае простейших
кристаллов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
En |
D |
|
|
1 E1 C |
2 E2 C |
3 E3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
, |
|||||||||
Поскольку вектор решетки в общем виде выражается как R |
|
|
|
|
a |
n a |
n a |
|||||||||||||||||||||||
вектор обратной решетки может быть записан в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
El |
D |
l |
1 E1 C |
l |
2 E2 C |
l |
3 E3 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
K |
|
b |
|
|
b |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K r |
|
|
|
|
|
|
|
E |
|||
где l1; l2; l3 — целые числа. Можно показать, что функция ej El E |
|
|
|
|
|
|
|
|||||||||||||||||||||||
в случае переменных r |
||||||||||||||||||||||||||||||
периодична, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
El EC En |
|
|
ej El E e |
El En |
|
e |
El |
E e |
|
|
1 |
|
1 C |
2 2 C |
3 |
3 |
|
|
|
e |
El E : |
|
(467) |
||||||
|
j K .r R |
/ |
D |
K r |
j K R |
|
D |
|
j K r |
j 2 .m |
l |
|
|
m l |
m |
l |
/ |
D |
|
|
j K r |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
С точки зрения многочисленных приложений, очень важно, что периодическая функ-
|
E C |
En |
|
D |
E |
|
|
|
|
|
|
|
|
|
|
|
ция |
F.r |
/ |
|
F.r / может быть представлена в виде ряда Фурье |
||||||||||||
|
R |
|
||||||||||||||
|
|
|
|
|
|
|
|
X |
G.k /ej |
El E ; |
|
|||||
|
|
|
|
|
F.r / |
D |
|
|||||||||
|
|
|
|
|
|
E |
|
El |
K r |
|
||||||
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
причем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
j |
El |
|
|
|
|
|
|
|
|
G. El D V VZ |
F.rE/e |
E dV: |
|||||||||
|
|
|
|
|
K / |
|
|
|
|
|
|
K r |
|
|||
|
|
|
|
|
|
|
|
|
|
E C |
El |
|
||||
Теперь рассмотрим решение, относящееся |
к |
: |
||||||||||||||
|
k |
|
K |
|||||||||||||
|
.r / e |
EC El E u |
|
.r / e |
E E |
ej El E u |
|
EC El E D |
j .k K /r |
EC El E D |
j kr |
K r |
EC El |
||
|
h |
|
|||||
k K |
|
|
k K |
|
|
|
k K |
i
.rE/ :
Функция в квадратных скобках периодична, так как, исходя из уравнения (467), периодичны все ее члены.
Таким образом, видно, что решение данного уравнения опять представлено в виде волны Блоха, определяемой с помощью уравнения (457), с тем, разумеется, различием,
что теперь при сомножителе ErE стоит другая периодическая функция. Следовательно,
k
j
e
встает вопрос, получают ли таким способом фактически различные решения?
226

b1 D 2a i I b2 D 2a j I b3 D 2a k
а)
b1 D 2a . i j C k/I b2 D 2a .i C j C k/I b3 D 2a . i C j k/
б)
b1 D 2a .i C k/I b2 D 2a .j i /I b3 D 2a .k j /
в)
Рис. 124. Пространство обратной решетки, или E-пространство, и первая и вторая зоны Бриллю- k
эна.
а — простая кубическая решетка; б — кубическая гранецентрированная решетка; в — кубическая объемно-центрированная решетка (вторые зоны Бриллюэна приведены не в масштабе).
227
Для того чтобы решить уравнение, введем функцию k |
K |
.r / |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
EC El |
E |
|
уравнение (453). Отсюда получим следующие соотношения: |
|
||||||||||||
2m E |
|
4 |
|
2m E |
C |
E |
EC El |
E D |
EC El |
||||
~2 |
|
2 |
|
~2 |
|
|
|
K r |
|
|
|
|
|
|
.k |
|
|
/ j |
|
kgrad |
|
Wp .r / |
ej El E uk K |
.r / |
|
Wk |
K |
в дифференциальное
h |
EC El |
E i |
|
ej El E uk K |
.r / : |
|
K r |
|
Эта зависимость идентична дифференциальному уравнению (461), так что тождественны и их решения. Можно выбрать теперь следующие соотношения:
Wn. E |
D |
|
n |
E C El |
I |
||
k/ |
|
W |
.k |
K / |
|
||
unk .r / |
|
ej El E un;k K .r / |
|||||
E |
E |
D |
|
K r |
EC El E I |
||
|
D |
||||||
k |
K |
.r / |
nk .r /: |
|
|||
n; EC El E |
E E |
|
|||||
Таким образом, видно, что значения энергии в обратной решетке, т.е. в E-пространстве, k
также периодичны.
Можно теперь утверждать, что соотношения, записанные для начальной и конечной точек кристалла, должны быть тождественно равны:
.rE/ D .rE C G1aE1/ D .rE C G2aE2/ D .rE C G3aE3/;
причем G1, G2, G3 обозначают числа элементарных ячеек в конечном кристалле. Если принять во внимание уравнение (464), то можно это условие записать следующим образом:
|
|
|
e |
|
|
1 E E1 |
|
|
ej G2 E E2 |
|
|
|
|
e |
|
3 E E3 |
|
1; |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
j G ka |
|
D |
|
|
|
ka |
|
D |
|
j G ka |
D |
|
|
|
|
|
|
|
||||||||||
а отсюда следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ka |
|
|
|
|
|
|
|
2 |
|
; ka |
|
D |
g |
|
|
2 |
; ka |
|
|
g |
|
2 |
; |
|
|
|||||||||
|
D g1 G1 |
|
2 G2 |
|
|
|
|
|
||||||||||||||||||||||||||
EE1 |
|
|
|
|
EE2 |
|
|
|
|
EE3 D |
|
3 G3 |
; |
|
||||||||||||||||||||
gi D 1; 2; : : : ; Gi I i D 1; 2; 3; : : : |
|
|
|
|
|
|
Ei |
|
||||||||||||||||||||||||||
E D |
k |
1 E1 C |
|
2 E2 C |
|
3 E3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
и принять |
||||||||||||||
Предположим, что k |
|
|
|
b |
|
|
k b |
|
k |
b |
|
. Если умножить обе части на a |
||||||||||||||||||||||
во внимание уравнение (464), то получим соотношение |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
EEi |
D |
|
i Ei Ei D |
i |
2 : |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
ka |
|
k b a |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|||||||||
ka |
2 .g |
=G |
/ придает формуле законченность: |
|
||||||||||||||||||||||||||||||
Соотношение EEi D |
|
g1 |
|
|
i |
|
i |
|
g2 |
|
|
|
|
g3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
k |
|
b |
|
C |
|
b |
|
|
b |
; |
|
g |
i D |
1; 2; : : : ; G |
: |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
E D |
G1 |
E1 |
|
G2 E2 C G3 E3 |
|
|
|
|
|
|
|
|
|
i |
|
|
||||||||||||||||||
Так как число элементарных ячеек, содержащихся в конечном кристалле, очень вели-
ко, допустимые значения E распределяются в E-пространстве практически непрерывно. k k
Как теперь можно представить или наглядно изобразить зависимость энергии от E, k
т.е. функцию E ? Трудность заключается в том, что речь идет об одновременном
W .k/
пространственном изображении скалярных функций вектора:
E E E
W1.k/; W2.k/; : : : ; Wn.k/; : : :
В одномерном случае мы имеем три возможности (рис. 120, б).
Теперь дело упрощает то, что n E в E-пространстве претерпевает изменение с
W .k/ k
периодом El . Поэтому достаточно разделить E-пространство на части, в которых по-
K k
вторяются значения n. Эти части E-пространства и являются зонами Бриллюэна — это
W k
зоны обратного пространства, характеризуемые следующими свойствами:
228

1)объем каждой зоны равен объему элементарной ячейки в обратном пространстве;
2)каждая зона может быть сведена к так называемой первой зоне Бриллюэна тем, что ее отдельные части смещаются на соответствующий вектор обратной решетки27;
3)первая зона Бриллюэна обладает свойством пространственного подобия в том смысле, что все пространство может быть сплошь заполнено подобными структурами.
Отдельные зоны Бриллюэна ограничены плоскостями, направленными перпендикулярно векторам обратной решетки и делящими их пополам. Уравнение этих плоскостей
2kK |
D |
K2 |
. Первая зона Бриллюэна есть наименьшая часть пространства |
имеет вид: E El |
El |
|
обратной решетки, ограниченная таким образом.
На рис. 123, а показаны первая, вторая и третья зоны Бриллюэна в случае «плоской» простой кубической решетки. Рассматривая этот рисунок, можно легко убедиться в справедливости только что перечисленных свойств зон Бриллюэна. На рис. 123, б
представлено соотношение D E в расширенной зонной схеме. (Эта схема соот-
W W .k/
ветствует правому графику рис. 120, б.) Здесь, следовательно, представлено в первой
зоне 1 E , во второй — 2 E и т.д. таким образом, что кривые проходят через точки,
W .k/ W .k/
обладающие равной энергией28. На рис. 120, в все транслировано в первую зону. (Сравни со средним графиком на рис. 120, б.)
В трехмерном случае установленные соотношения нельзя наглядно изобразить и в
случае простой кубической решетки. Даже для изображения 1 E необходим ряд плос-
W .k/
костей постоянной энергии: рис. 123, г соответствует только самому нижнему участку кривой среднего графика рис. 120, б или левой части рисунка 123.
Чтобы пояснить сложную структуру зоны Бриллюэна, мы изобразили на рис. 124
первую и вторую зоны Бриллюэна простейших типов решеток. |
|
|||
|
W |
n D |
k/ |
|
Естественно, если хотят проследить ход функций |
|
Wn. E |
в конкретном слу- |
|
чае, то в качестве исходных используют, с одной стороны, базисные векторы кристаллической решетки конкретного типа или набор соответствующих векторов обратной решетки; с другой стороны, необходимо составить конкретное уравнение, описывающее ход потенциала в зависимости от типа решетки. Эти математические выражения должны удовлетворять, разумеется, в случае потенциала — условию его периодичности (в rE-пространстве), а в случае функции состояний — теореме Флюге—Блоха.
Из многих методов нахождения приближенных решений хотим напомнить только два крайних случая: приближение свободных электронов и приближение сильной связи. В случае использования приближения свободных электронов мы используем в качестве исходного соотношение плоской волны
|
1 |
|
kr |
|
||
.r / |
|
|
|
|
ej E E ; |
(468) |
|
|
|
|
|||
E |
D p |
V |
|
|
|
|
27Бриллюэн показал, что все области, имеющие одинаковую штриховку (рис. 123, а) могут быть соединены единственным образом так, чтобы образовать квадрат, тождественно равный центральному. При
этом любые две точки налагающихся квадратов отличаются друг от друга на вектор E. Поэтому одинаково
K
заштрихованные области являются областями одной и той же зоны. Процесс объединения таких заштри-
хованных площадок в одну зону заключается в трансляции их в центральную зону на вектор E-типа, т.е.
K
площадки нельзя поворачивать или накладывать обратной стороной.
28Другими словами, энергия может быть представлена как многозначная функция точек первой зоны
вместо того, чтобы рассматриваться как однозначная разрывная функция на всей E-плоскости.
K
229
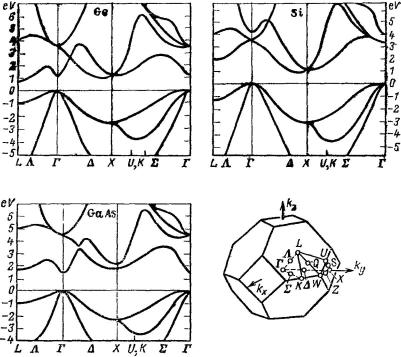
k/ |
|
Рис. 125. Практически важный способ изображения Wn D Wn. E |
для Ge, Si и GaAs. Приведены |
первая зона Бриллюэна и важнейшие оси симметрии, вдоль которых вычислены значения W |
|
(Marvin et al. Phys. Rev. vol. 141, S. 789). |
|
которое, разумеется, удовлетворяет теореме Флюге—Блоха. Влияние потенциальной энер-
гии учитывается как возмущение. Подробный расчет показывает, что при значениях k, |
|||
соответствующих условию 2kK |
D |
K2 |
E |
, т.е. на границах зоны Бриллюэна, обнаружива- |
|||
E El |
El |
|
|
ется существенное отклонение от состояния свободного электрона (например, дискрет-
ность функции D E ).
W W .k/
В случае использования приближения сильной связи исходят из атомных функций состояния и комбинируют их таким образом, чтобы полученное решение удовлетворяло
теореме Флюге—Блоха: |
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j E Ei |
|
|
|
|
|
|
|
|
|
|
|
E |
|
E |
|
D |
|
kR |
|
E |
R |
/: |
|
(469) |
|
|
|
|
k |
.r / |
|
e |
|
a |
.r |
|
|||||
|
|
|
|
|
|
|
|
|
|
Ei |
|
|
|
|||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
.r |
R |
/ |
|
|
|
|
|
|
|
|
|
|
|
В этом выражении |
a |
E |
Ei |
|
является собственной функцией атома, находящегося |
|||||||||||
R |
. Величине |
|
|
соответствует собственное значение W |
|
. |
||||||||||
в точке решетки Ei |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
0 |
|
В случае простой кубической объемной решетки расчеты в результате использования упрощающих предположений гипотез приводят к соотношению
W . E |
D |
W |
0 C |
K |
C |
x |
a |
C |
y |
C |
z |
k/ |
|
|
|
2J .cos k |
|
cos k a |
|
cos k a/: |
Здесь K и J обозначают константы, зависящие от атомного потенциала и функции a. На рис. 123 представлены по существу поверхности уровня
E 0 D CONST
W .k/ W K :
В случае сложных решеток усложняется и форма представления соответствующих результатов. На рис. 125 показан график, полученный с помощью расчетов, основанных на более точных приближенных методах для важных, с практической точки зрения, случаев — для германия (Ge), кремния (Si) и арсенида галлия (GaAs).
230
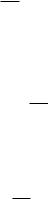
27.3Движение электронов во внешнем поле. Понятие эффективной массы
Как было показано ранее, поведение электронов в потенциальном поле твердого тела довольно сложно, хотя в качестве основы для оценки была взята сильно упрощенная модель. При таких обстоятельствах представление о свободных электронах, конечно, уже неприемлемо. Во многих случаях — особенно при рассмотрении условий прохождения тока в полупроводниках — оказывается совершенно необходимым введение несколько условного понятия — эффективной массы. Речь идет о том, что электрон под влиянием
F |
D |
q |
E, совершает направленное |
внешней силы, например электрического поля Eвнешн |
|
e E |
движение. Так возникает электрический ток. Разумеется, ускорение при этом не может быть вычислено при помощи соотношения
F |
m |
d vE |
; |
Eвнешн D |
|
dt |
|
так как действующая внутри кристалла сила, обусловленная потенциальным полем решетки, значительно больше приложенной внешней силы. Поэтому истинным уравнением движения является
F |
F |
m |
d vE |
: |
Eвнешн C Eвнутр D |
|
dt |
|
|
Разумеется, однако, что это явление может быть описано и так, как будто действитель-
F |
. Тогда m |
эфф |
означает в уравнении |
|
|
ности существует лишь сила Eвнешн |
|
|
|
||
|
F |
m |
|
d vE |
(470) |
|
эфф dt |
||||
|
Eвнешн D |
|
|
||
не истинную массу электрона, а соответствующим образом выбранную величину, на которую должно быть умножено фактическое ускорение d v=E dt , полученное вследствие
суммарного воздействия сил Eвнешн и Eвнутр. Естественно, что в случае свободного элек-
F F
D 0/ так называемая эффективная масса совпадает с действительной. Чтобы прийти к понятию эффективной массы, прежде всего, определим скорость
электрона. В упрощенном квантовомеханическом представлении электрон описывается как волновой пакет, причем групповая скорость волн совпадает со скоростью электрона. Эта групповая скорость и, следовательно, скорость электрона равна:
v D |
d! |
D |
2 d W |
: |
(471) |
||
|
|
|
|
||||
d k |
h d k |
||||||
Эту важную зависимость мы можем несколько уточнить. Ожидаемое значение импульса, соответствующего решению
|
|
|
u .r /ej E E ; |
||||
|
D |
|
k |
E |
kr |
||
|
|
|
|||||
получают путем умножения скаляров ( |
; p; |
|
), где p обозначает оператор, импульса: |
||||
|
|
h |
|
grad : |
|||
|
|
|
|||||
|
2 j |
||||||
Отсюда |
|
h |
|
VZ |
|
|
|
< p >D |
|
|
|
grad dV: |
|||
|
|
||||||
2 j |
|
||||||
231

В результате несколько более тщательного подсчета получим:
< p > |
D |
2 |
m |
|
|
k/: |
|
||||
h |
|
E |
|
||||||||
|
|
|
|
|
|
|
|
grad k W . E |
|
||
В соответствии с этим ожидаемое значение скорости |
|
||||||||||
|
|
|
|
D h |
E |
|
|
|
|||
< |
v |
> |
|
2 |
|
|
|
k/: |
(472) |
||
|
|
|
|
|
|
||||||
|
|
|
|
grad k W . E |
|
||||||
Пусть теперь сила F воздействует на электрон, движущийся вперед со скоростью v.
Тогда изменение энергии составит: |
|
|
|
|
|
|
|
|
|
|
|
d W |
|
D F v: |
|
(473) |
|||
|
|
|
|
|
|
||||
|
|
|
dt |
|
|||||
После подстановки значения скорости получим: |
|
|
|||||||
|
d W |
D |
2 |
F |
d W |
: |
(474) |
||
|
|
|
|
|
|
||||
|
dt |
|
h |
d k |
|||||
Эти изменения энергии можно записать и несколько иначе:
|
|
|
|
|
|
d W |
|
|
|
d W d k |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
: |
|
|
|
|
(475) |
|
|
|
|
|
|
|
dt |
|
d k |
dt |
|||||||||||||||
Сравнивая оба последних уравнения, получаем: |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
F D |
|
h d k |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
(476) |
||||||||
|
|
|
|
|
|
2 |
dt |
|
|
|
|
|
||||||||||||
Исходя из уравнения (471), найдем ускорение: |
|
|
|
|
|
|
||||||||||||||||||
dv |
2 d d W |
|
|
|
|
|
|
|
2 d 2W d k |
|
||||||||||||||
|
|
D |
|
|
|
|
|
|
D |
|
|
|
|
|
: |
|||||||||
|
dt |
h |
dt |
d k |
|
h |
d k2 |
dt |
||||||||||||||||
Если вместо d k=dt подставить его значение из предыдущего уравнения, то получит-
ся: |
|
|
|
2 d 2W |
|
|
|
||
|
dv |
2 |
|
1 |
|
||||
|
|
D |
|
|
|
|
F D |
|
F: |
|
dt |
h |
|
d k2 |
mэфф |
||||
Таким образом, видно, что следующая формула дает значение эффективной массы:
1 |
2 |
|
2 d 2W |
|
|
||
|
D |
|
|
|
: |
(477) |
|
mэфф |
h |
|
d k2 |
||||
Если исходить из уравнения (472), то можно записать уравнения в несколько ином виде:
|
d W |
|
|
|
F v |
|
F |
2 |
grad |
|
W .k/ |
|
|
|||||
|
|
|
|
|
|
|
|
k |
|
|
||||||||
|
dt |
|
|
|
D |
|
E |
E D |
E |
|
|
|
E |
I |
||||
|
|
|
|
|
|
|
h |
|
|
E |
|
|
||||||
|
|
|
d W |
|
|
|
|
|
|
|
|
|
k |
|
|
|
||
|
|
|
|
|
|
|
|
|
k/ |
d E |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
dt |
|
D |
grad k W . E |
dt |
I |
|
|
||||||
|
|
|
|
|
|
|
|
E |
|
|
|
|
||||||
d v |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
k |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d E |
||
E |
|
|
|
|
|
|
|
grad k .grad k W .k// |
|
: |
||||||||
dt |
D |
h |
|
|
||||||||||||||
|
|
|
E |
E |
|
E |
dt |
|||||||||||
232
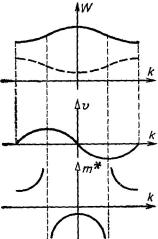
Для характеристики эффективной массы используют, таким образом, тензор со сле-
дующими компонентами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
d 2W |
|
|
d 2W |
|
|
d 2W |
1 |
|
|
|||||||
|
|
|
d kx2 |
|
d kx d ky |
|
d kx d kz |
|
|
|||||||||||
|
B |
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
C |
|
|
||||
.m / 1 |
B |
2 |
W |
|
|
d |
2W |
|
|
d 2W |
C |
: |
(478) |
|||||||
d |
|
|
|
2 |
|
|
|
|
|
|
||||||||||
E |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
D B d ky d kx |
|
|
d ky |
|
d ky d kz |
C |
|
|
||||||||||||
|
@ |
|
|
d W |
|
|
d W |
|
|
d W |
A |
|
|
|||||||
|
B |
|
|
|
|
C |
|
|
||||||||||||
|
B |
|
|
|
|
|
|
|
|
|
C |
|
|
|||||||
|
d k d k |
x |
|
d k |
d k |
|
|
d k2 |
|
|
||||||||||
|
B |
z |
|
|
|
|
z |
|
y |
|
|
|
z |
C |
|
|
||||
Рис. 126. Значения скорости . |
d W =d k |
/ и эффективной массы |
.dv=d k/ |
1 |
электрона для |
|
|||||
второй зоны Бриллюэна. |
|
|
На рис. 126 приведена зависимость эффективной массы от волнового вектора. Как
видно из уравнения (477), эта масса пропорциональна радиусу кривизны функции E .
W .k/
Ее значение может равняться нулю и даже быть отрицательным. На графике приведена и скорость, так что можно наглядно проследить, что величина k в случае силы, действующей в соответствии с соотношением (476) увеличивается, в то время как скорость то возрастает, то уменьшается в зависимости от того, имеет ли эффективная масса отрицательное или положительное значение. Как только электрон в результате своего движения достигает правого края зоны, он отражается и вновь появляется на левом краю зоны.
233

28 Возможные типы зонных структур
Исходя из сказанного, рассмотрим возможные типы зонных структур в случае конкретного твердого тела. Расположим свободные атомы очень далеко один от другого, однако в соответствии с окончательной кристаллической структурой, и начнем сближать их до тех пор, пока они не займут окончательного положения равновесия. Энергетические уровни свободного атома расщепляются при этом на зоны, которые состоят из совокупности дискретных уровней. Степень расщепления зависит от взаимного расстояния атомов и может быть подсчитана с помощью методов, описанных выше. Таким образом, получают энергетические зоны, изображенные на рис. 117, согласно которому расщепление отдельных невозмущенных уровней можно рассматривать как функцию изменения постоянной решетки. Если рассмотреть изменение величины средней энергии от межатомного расстояния, то видно, что при совершенно определенном расстоянии между атомами она достигает минимального значения, соответствующего положению равновесия. Именно наличие этого минимума обусловливает возможность существования металлической связи. Если теперь при этом состоянии равновесия осуществить вертикальный разрез энергетической диаграммы, то получим зонную структуру металла, характерную для состояния равновесия.
а) |
б) |
Рис. 127. Различные варианты расщепления атомных уровней. Взаимное расположение разрешенных и запрещенных зон определяет, является кристалл проводником или изолятором (а): 1 — проводник; 2 — изолятор; 3 — полупроводник; 4 — свободная зона; 5 — заполненная зона; 6 — запрещенная зона. Зона проводимости может возникнуть за счет перекрытия различных зон, как, например, в случае меди (б).
С точки зрения электропроводности решающее значение имеет изучение фактической заселенности расщепленных энергетических уровней. Возьмем, например, одновалентный металл. Соответствующий s-уровень расщепляется на G3 уровней. Согласно принципу Паули на каждом энергетическом уровне может быть по два электрона с противоположными спинами. Всего в металле имеется G3 электронов, так что занята лишь половина возможных уровней. Не входя в детальное исследование взаимодействия электрического поля и электронов, мы знаем, что каждый электрон в случае существования электрического тока приобретает определенную энергию, передаваемую ему электрическим полем, следовательно, он должен перейти на более высокий энергетический уровень, чем тот, на котором он находился прежде. Однако это возможно лишь тогда, когда в непосредственной близости к занятым уровням есть свободный, разрешенный уровень. Это справедливо и для одновалентных металлов, о которых идет речь. Можно
234
было бы ожидать, что в случае с двухвалентными металлами, у которых все уровни заполнены, дальнейшее поглощение энергии электронами и, следовательно, прохождение электрического тока в металлах невозможны. Однако опыт показывает, что это не так: возбужденные уровни свободного атома также расщепляются, и обе зоны в состоянии равновесия могут перекрываться, как показано на рис. 127, а. Таким образом, разрешенные энергетические уровни примыкают к заполненным энергетическим уровням, минуя расположенные между ними запрещенные зоны, обеспечивая тем самым прохождение электрического тока и в двухвалентных металлах.
а) |
б) |
Рис. 128. Кристаллическая решетка алмаза (а). Подобный образом кристаллизуются кремний и германий, ширина запрещенной зоны между валентной зоной и зоной проводимости составляет соответственно для С, Si и Ge 6, 1 и 0.7 эВ; кристаллическая решетка графита (б).
Таким образом, проводником является такое твердое тело, у которого самая верхняя зона, так называемая зона проводимости, еще не полностью заполнена электронами. Рисунок 127 показывает, как образуются такие не до конца заполненные зоны в проводниках, имеющих большое практическое значение. В изоляторе электронами заполнен каждый уровень этой зоны. Различные кристаллические модификации одного и того же материала могут вести себя по-разному. Если рассмотреть сильно различающиеся (рис. 128, а и б) расположением атомов в решетке различные модификации углерода — алмаз и графит, то окажется неудивительным, что первый является изолятором, а последний — проводником. Если заполненная зона проводимости отделена от расположенной над ней незаполненной энергетической зоны только узкой запрещенной зоной, то достаточно теплового движения электронов, чтобы забросить электроны в незаполненную зону и обеспечить, таким образом, электрическую проводимость. Такой материал называют полупроводником.
Перекрытие зон, а следовательно, и сам факт, является ли твердое тело проводником, полупроводником или изолятором, определяются постоянной решетки, т.е. расстоянием между атомами, образующими решетку. Оно может быть изменено с помощью механического воздействия, что указывает, следовательно, на взаимосвязь проводимости и механических напряжений в решетке.
235
