
Российский университет дружбы народов
ИНСТИТУТ ИНОСТРАННЫХ ЯЗЫКОВ
«ПАРАДОКСЫ БЕРТРАНА»
РЕФЕРАТ
Руководитель: Курышева Л.О.
Выполнила: Яндовицкая Анастасия
Группа ЗР-201
Дата выполнения: 21.10.2015
Дата проверки: _________
Москва – 2015
Парадоксы Бертрана
Жозеф Луи Франсуа Бертран (фр. Joseph Louis François Bertrand; 11 марта 1822, Париж – 5 апреля 1900, Париж) — французский математик, работавший в области теории чисел, дифференциональной геометрии, теории вероятности и термодинамики.
Парадокс Бертрана -проблема в пределах классической интерпретации теории вероятности. Жозеф Бертран ввел его в своей работе Calcul des probabilités, написанной в 1889 году, как пример, чтобы показать, что вероятности не могут быть хорошо определены, если механизм или метод, который производит случайную переменную, ясно не определены.
Формулировка проблемы Бертрана
Парадокс Бертрана идет следующим образом: предположим, что в окружность случайным образом вписан равносторонний треугольник. Допустим, что наугад в данной окружности проводится хорда. Какова вероятность того, что проведенная нами хорда будет длиннее стороны равностороннего треугольника?
Для решения этой задачи Бертран предложил три решения. Каждое из этих решений очевидно верно. Но каждое из этих решений дает разный результат.
Метод «случайных конечных точек»
Для
осуществления данного метода нам
необходимо наудачу выбрать две точки
на окружности и провести через них
хорду. Чтобы посчитать искомую вероятность,
представим, что треугольник повернут
так, что одна из его вершин совпадает с
концом хорды. Заметим, что если другой
конец хорды лежит на дуге между двумя
другими вершинами треугольника, то
длина хорды больше стороны треугольника.
Длина рассмотренной дуги равна трети
длины окружности, следуя классическому
определению, искомая
вероятность
равна ![]() .
.
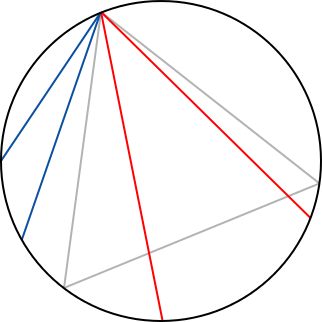
На схеме: случайные хорды, выбранные по методу 1: красные – длиннее стороны треугольника, синие – короче.
Метод «случайного радиуса»
Для
осуществления данного метода нам
потребуется зафиксировать радиус
окружности и наудачу выбрать точку на
радиусе. Построим хорду, перпендикулярную
зафиксированному радиусу, проходящую
через выбранную точку. Для нахождения
искомой вероятности, представим, что
треугольник повёрнут так, что одна из
его сторон перпендикулярна зафиксированному
радиусу. Хорда длиннее стороны
треугольника, если ее центр ближе к
центру, чем точка пересечения треугольника
с зафиксированным радиусом. Сторона
треугольника делит пополам радиус,
следовательно, вероятность выбрать
хорду длиннее стороны треугольника ![]() .
.
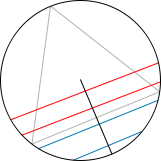
На схеме: выбранные хорды по методу 2.
Метод «случайного центра»
Для
осуществления данного метода нам
необходимо выбрать наудачу произвольную
точку внутри круга и построить хорду с
центром в выбранной точке. Хорда длиннее
стороны равностороннего треугольника,
если выбранная точка находится внутри
круга, вписанного в треугольник. Площадь
вписанного круга есть 1/4 от площади
большего, соответственно, исходная
вероятность равна ![]() .
.
На схеме: Случайные хорды по методу 3.

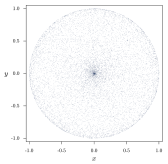
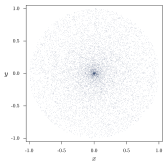
Выбор метода также может быть изображён следующим образом. Хорда однозначно задаётся ее серединой. Все три метода, описанные выше, дают различное, каждый своё, распределение середины. Методы 1 и 2 представляют два разных неравномерных распределения, в то время как третий метод даёт равномерное распределение. С другой стороны, если посмотреть на изображения хорд ниже, то заметно, что хорды в методе 2 дают равномерно закрашенный круг, а 1-й и 3-й методы не дают такой картины.




Могут быть придуманы и другие распределения; многие из них дадут разные доли хорд, имеющих большую длину, чем сторона вписанного треугольника.
