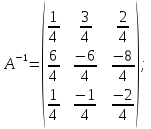- •Лекция № 1.
- •Вопрос 1. Основные сведения о матрицах.
- •Виды матриц
- •Вопрос 2. Операции над матрицами и их свойства.
- •Теорема Лапласа
- •Вопрос 2. Свойства определителей.
- •Лекция № 3
- •Лекция № 4
- •Вопрос 1. Системы линейных алгебраических уравнений слу (Основные понятия и определения).
- •Вопрос 2. Методы решения систем линейных уравнений.
- •1) Метод обратной матрицы (матричный метод) решения систем n линейных уравнений с n неизвестными.
- •2) Правило Крамера решения систем n – линейных уравнений с n – неизвестными.
- •Формулы:
- •Лекция № 5
- •Вопрос 1. Метод Гаусса решения систем линейных уравнений.
- •Алгоритм метода Гаусса:
- •Вопрос 2. Исследование систем линейных уравнений.
- •Лекция № 6
- •Вопрос 1. Системы линейных однородных уравнений.
- •Лекция № 7
- •Вопрос 1. Модель Леонтьева многоотраслевой экономики.
- •Модель Леонтьева многоотраслевой экономики (модели межотраслевого баланса)
- •Балансовые соотношения
- •Линейная модель многоотраслевой экономики
- •Лекция № 8
- •Вопрос 1. Векторы (основные понятия и определения).
- •Вопрос 2. Линейные операции над векторами.
- •Свойства:
- •Вопрос 3.
- •Вопрос 4. Формулы для нахождения длины вектора, расстояния между точками и угла между векторами.
- •Лекция № 9
- •Вопрос 1. Векторное произведение векторов
- •Геометрический смысл.
- •Свойства векторного произведения.
- •Вопрос 2. Выражение векторного произведения через координаты.
- •Вопрос 3. Смешанное произведение векторов
- •Геометрический смысл
- •Вопрос 4. Выражение векторного и смешанного произведения через координаты перемножаемых векторов.
- •Вопрос 5. Уравнение плоскости, проходящей через три данные точки.
- •Лекция № 10
- •Вопрос 1. Понятие векторного (линейного) пространства.
- •Вопрос 2. Размерность и базис векторного пространства.
- •Вопрос 3. Линейная оболочка и ее свойства.
- •Свойства линейной оболочки
- •Вопрос 4. Евклидово пространство.
- •Вопрос 5. Ортогональный и ортонормированный базис.
- •Вопрос 6. Переход к новому базису.
- •Лекция № 11
- •Вопрос 1. Линейные операторы.
- •Вопрос 2. Собственные векторы и собственные значения линейного оператора (матрицы).
- •Вопрос 3. Квадратичные формы.
- •Лекция № 12
- •Вопрос 1. Линейная модель обмена (международной торговли).
- •Лекция № 13
- •Вопрос 1. Уравнения прямой (различные виды). Параметрические уравнения прямой.
- •Уравнение прямой проходящей через две данные точки
- •Угловой коэффициент прямой. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.
- •Уравнение прямой, проходящей через данную точку с данным нормальным вектором (нормалью).
- •Общее уравнение прямой.
- •Вопрос 2. Формула угла между прямыми.
- •Вопрос 3. Условия параллельности и перпендикулярности прямых.
- •Вопрос 4. Формула расстояния от точки до прямой.
- •Лекция № 16
Вопрос 4. Евклидово пространство.
Введем в пространстве R метрику, т.е. операции нахождения длины вектора и угла между векторами.
Для
этого определим операцию скалярного
произведения векторов
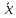 и
и
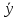 .
.
Если
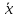 = (
= (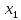 ,
,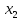 ,
…,
,
…,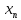 ),
),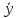 = (
= ( ,
,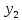 ,
…,
,
…,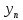 ),
то
),
то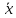 ·
·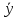 =
=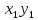 +
+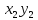 + … + +
+ … + +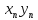 .
Обозначается следующим образом:
.
Обозначается следующим образом:
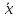 ·
·
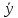 = (
= (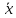 ,
,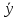 ).
).
Следовательно,
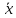 ·
·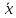 = (
= (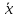 ,
,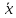 )
)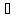 │
│ │2
=
│2
=
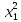 +
+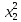 + … +
+ … +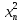 ,
,
т. е.
│ │=
│=
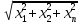 ‒ длина (норма) вектора.
‒ длина (норма) вектора.
Обозначим
= (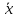 ,
,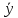 ).
).
Тогда
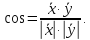
Линейное векторное пространство Rназывается евклидовым, если в нем задана метрика.
Вопрос 5. Ортогональный и ортонормированный базис.
Система векторов e1, е2, …, еn называется ортогональной, если (еi ,еj) = 0 при i j, и нормированной, если │еi│ = 1 для всех i = 1, 2,..., n.
Если векторы системы ортогональны и нормированы, они называются ортонормированными.
Пример. Чтобы нормировать ненулевой вектор, необходимо разделить его на норму.
Пусть задан вектор x = (1, –1, 2, 0).
Его
норма |x|
=
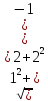 .
Нормированный вектор имеет вид
.
Нормированный вектор имеет вид
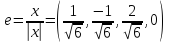 .
Его длина │е│=
1.
.
Его длина │е│=
1.
Теорема 1. Ортонормированная система векторов линейно независима.
Теорема 2. Во всяком n‒ мерном евклидовом пространстве существует ортонормированный базис.
Вопрос 6. Переход к новому базису.
Пусть
в пространстве R
заданы два базиса: старый
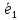 ,
,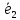 ,
… ,
,
… ,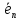 и новый
и новый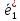 ,
,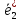 ,
… ,
,
… ,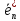 .
.
Выразим связь между базисами, разложив векторы нового базиса по векторам старого базиса:
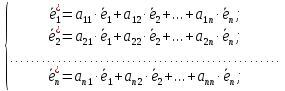
Связь
между базисами задается матрицей
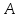 ,
записанной в транспонированном виде:
,
записанной в транспонированном виде:
А
=
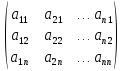
Координаты
вектора в новом базисе находятся с
помощью обратной матрицы
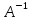 .
.
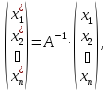
где
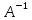 – матрица перехода от старого базиса
к новому;
– матрица перехода от старого базиса
к новому;


Пример.
|
Дано |
Решение |
|
В
базисе
|
1)
Докажем, что векторы
т. е. образуют базис. Для этого составим их линейную комбинацию и приравняем ее к нулевому вектору.
Получим: |
|
Доказать,
что векторы
| |
|
Следовательно, получим однородную систему:
∆ =
Следовательно,система
имеет единственное решение
2) Разложим векторы нового базиса по векторам старого базиса.
Координаты
вектора
Ã=
| |
Лекция № 11
Вопрос 1. Линейные операторы.
Рассмотрим
два линейных векторных пространства:
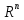 – размерности
– размерности
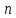 и
и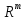 – размерности
– размерности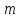 .
.
Определение.
Если задан закон или правило, по которому
каждому вектору
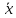 пространства
пространства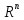 ставится в соответствие единственный
вектор ȳ пространства
ставится в соответствие единственный
вектор ȳ пространства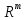 ,
то говорят, что задан оператор (отображение)
как функция
,
то говорят, что задан оператор (отображение)
как функция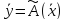 пространства
пространства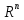 в пространство
в пространство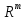 ,
т.е.
,
т.е.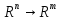 .
.
Вектор
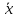 – прообраз вектора
– прообраз вектора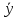 ,
вектор
,
вектор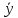 – образ
– образ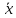 при этом отображении.
при этом отображении.
Оператор
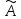 называетсялинейным,
если выполняются следующие два условия:
называетсялинейным,
если выполняются следующие два условия:
1.
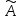 (
(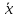 +
+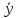 )
=
)
=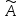 (
(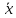 )
+
)
+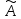 (
(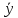 )
– аддитивность;
)
– аддитивность;
2.
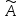 (·
(·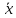 )
=·
)
=·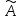 (
(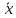 )
– однородность.
)
– однородность.
Равенство
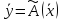 можно
представить в виде матричного уравнения:
можно
представить в виде матричного уравнения:
Y = A · X,
где
A
– матрица линейного оператора
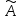 .
В координатном виде получим:
.
В координатном виде получим: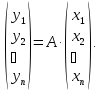
Зависимость
между матрицами
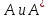 одного и того же оператора
одного и того же оператора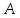 в разных базисах задается формулой:
в разных базисах задается формулой:
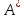 =
=
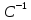 ·
·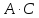 ,
,
где
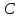 – матрица перехода от старого базиса
к новому.
– матрица перехода от старого базиса
к новому.
Пример:
Линейный
оператор
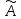 задан матрицей:
задан матрицей:
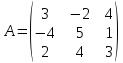 ;
;
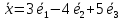 ;
;
Найти:
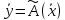
Решение:
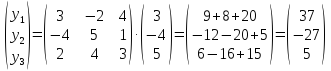 ;
;
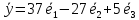 .
.

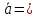 (1;
1; 0),
(1;
1; 0), 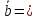 (1;
–1; 1),
(1;
–1; 1),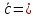 (–3;
5; –6),
(–3;
5; –6),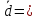 (4;
–4; 5).
(4;
–4; 5).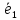 ,
,
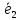 ,
,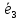 .
. и
и
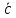 являются линейно независимыми,
являются линейно независимыми, ·
·
 +
+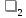 ·
·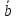 +
+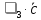 =
=
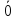 .
.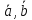 и
и
 сами образуют базис и найти координаты
вектора
сами образуют базис и найти координаты
вектора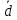 в этом базисе.
в этом базисе.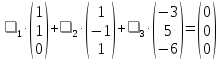
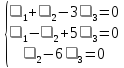
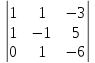 = 6–
3 + 0 –
0 –
5 + 6 = 4
0
= 6–
3 + 0 –
0 –
5 + 6 = 4
0 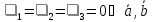 и
и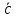 –
линейно независимые, т. е. образуют
базис.
–
линейно независимые, т. е. образуют
базис.
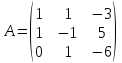 .
. .
.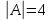 ;
;

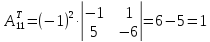 ;
;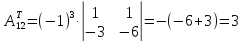 ;
;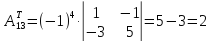 ;
;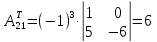 ;
;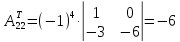 ;
;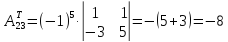 ;
;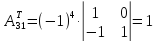 ;
;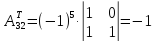 ;
;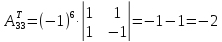 ;
;