
- •Лекция № 1.
- •Вопрос 1. Основные сведения о матрицах.
- •Виды матриц
- •Вопрос 2. Операции над матрицами и их свойства.
- •Теорема Лапласа
- •Вопрос 2. Свойства определителей.
- •Лекция № 3
- •Лекция № 4
- •Вопрос 1. Системы линейных алгебраических уравнений слу (Основные понятия и определения).
- •Вопрос 2. Методы решения систем линейных уравнений.
- •1) Метод обратной матрицы (матричный метод) решения систем n линейных уравнений с n неизвестными.
- •2) Правило Крамера решения систем n – линейных уравнений с n – неизвестными.
- •Формулы:
- •Лекция № 5
- •Вопрос 1. Метод Гаусса решения систем линейных уравнений.
- •Алгоритм метода Гаусса:
- •Вопрос 2. Исследование систем линейных уравнений.
- •Лекция № 6
- •Вопрос 1. Системы линейных однородных уравнений.
- •Лекция № 7
- •Вопрос 1. Модель Леонтьева многоотраслевой экономики.
- •Модель Леонтьева многоотраслевой экономики (модели межотраслевого баланса)
- •Балансовые соотношения
- •Линейная модель многоотраслевой экономики
- •Лекция № 8
- •Вопрос 1. Векторы (основные понятия и определения).
- •Вопрос 2. Линейные операции над векторами.
- •Свойства:
- •Вопрос 3.
- •Вопрос 4. Формулы для нахождения длины вектора, расстояния между точками и угла между векторами.
- •Лекция № 9
- •Вопрос 1. Векторное произведение векторов
- •Геометрический смысл.
- •Свойства векторного произведения.
- •Вопрос 2. Выражение векторного произведения через координаты.
- •Вопрос 3. Смешанное произведение векторов
- •Геометрический смысл
- •Вопрос 4. Выражение векторного и смешанного произведения через координаты перемножаемых векторов.
- •Вопрос 5. Уравнение плоскости, проходящей через три данные точки.
- •Лекция № 10
- •Вопрос 1. Понятие векторного (линейного) пространства.
- •Вопрос 2. Размерность и базис векторного пространства.
- •Вопрос 3. Линейная оболочка и ее свойства.
- •Свойства линейной оболочки
- •Вопрос 4. Евклидово пространство.
- •Вопрос 5. Ортогональный и ортонормированный базис.
- •Вопрос 6. Переход к новому базису.
- •Лекция № 11
- •Вопрос 1. Линейные операторы.
- •Вопрос 2. Собственные векторы и собственные значения линейного оператора (матрицы).
- •Вопрос 3. Квадратичные формы.
- •Лекция № 12
- •Вопрос 1. Линейная модель обмена (международной торговли).
- •Лекция № 13
- •Вопрос 1. Уравнения прямой (различные виды). Параметрические уравнения прямой.
- •Уравнение прямой проходящей через две данные точки
- •Угловой коэффициент прямой. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.
- •Уравнение прямой, проходящей через данную точку с данным нормальным вектором (нормалью).
- •Общее уравнение прямой.
- •Вопрос 2. Формула угла между прямыми.
- •Вопрос 3. Условия параллельности и перпендикулярности прямых.
- •Вопрос 4. Формула расстояния от точки до прямой.
- •Лекция № 16
Вопрос 5. Уравнение плоскости, проходящей через три данные точки.
Пусть
плоскость проходит через точки М1
= (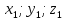 ),М2
=
(
),М2
=
( ) иМ3
= (
) иМ3
= ( ),
не лежащие на одной прямой иМ
(x,
y,
z)
– произвольная точка плоскости.
),
не лежащие на одной прямой иМ
(x,
y,
z)
– произвольная точка плоскости.

Векторы
 ,
, и
и ‒ компланарные, т.к. находятся в одной
плоскости. Следовательно,
‒ компланарные, т.к. находятся в одной
плоскости. Следовательно,
 ·
·
 ·
·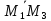 = 0.
= 0.
Запишем это равенство в координатной форме:

‒ уравнение плоскости проходящей через три данные точки.
Лекция № 10
Вопрос 1. Понятие векторного (линейного) пространства.
Вектор в n‒ мерном пространстве.
n ‒ мерным вектором называется упорядоченная совокупность n ‒ действительных чисел, записываемых в виде:
 =
(
=
( ,
, ,
…,
,
…, ),
),
где
 ‒i‒
компонента вектора
‒i‒
компонента вектора
 =
= .
.
Для n ‒ мерных векторов имеют место операции сложения и умножения на число, удовлетворяющие следующим свойствам:
1.
 +
+ =
= +
+ – коммутативность;
– коммутативность;
2.
 + (
+ ( +
+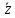 )
= (
)
= (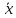 +
+ )
+
)
+ – ассоциативность;
– ассоциативность;
3.
( = (
= ( )
) – ассоциативность;
– ассоциативность;
4.
( +
+ )
=
)
= +
+  – дистрибутивность;
– дистрибутивность;
5.
 + (‒
+ (‒ )
=
)
= .
.
Линейным векторным пространством называется совокупность n ‒ мерных векторов с действительными компонентами, удовлетворяющих приведенным выше свойствам.
Вопрос 2. Размерность и базис векторного пространства.
Вектор
 называетсялинейной
комбинацией векторов
называетсялинейной
комбинацией векторов
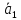 ,
,
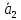 ,
…,
,
…,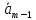 ,
если для любых чисел
,
если для любых чисел ,
, ,
…,
,
…, ,
не равных нулю одновременно, выполняется
равенство:
,
не равных нулю одновременно, выполняется
равенство:
 =
=
 ·
· +
+ ·
· + … +
+ … + ·
·
Векторы
 ,
, ,
…,
,
…, ,
называютсялинейно
зависимыми,
если их линейная комбинация равняется
нулевому вектору.
,
называютсялинейно
зависимыми,
если их линейная комбинация равняется
нулевому вектору.
 ·
·
 +
+ ·
·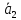 + … +
+ … + ·
· =
=
 (1)
(1)
В
противном случае векторы называются
линейно
независимыми,
т. е. равенство (1) выполнится только для
 =
= = … =
= … = = 0.
= 0.
Совокупность линейно независимых векторов векторного пространства R называется его базисом, а их количество называется размерностью векторного пространства.
Если в векторном пространстве Rимеется nлинейно независимых векторов, то размерность этого пространства обозначается dimR = n, dim – размерность (dimension).
Векторное
пространство размерности n
обозначается
 .
.
Теорема.
Если
векторы
 ,
, ,
… ,
,
… , образуют базис векторного пространства
образуют базис векторного пространства ,
то любой вектор
,
то любой вектор ,
можно единственным образом разложить
по этим векторам:
,
можно единственным образом разложить
по этим векторам:
 =
=
 +
+ + … +
+ … + .
.
Вопрос 3. Линейная оболочка и ее свойства.
Линейной оболочкой L (x1, x2) двух векторов x1 и x2, принадлежащих линейному пространству W, называется совокупность всех линейных комбинаций этих векторов
а = ·x1 + β · х2,где , β ϵR.
Иначе говоря, линейная оболочка состоит из бесконечного множества векторов а, представимых в виде линейных комбинаций векторов x1 и x2. В общем случае линейной оболочкой множества X векторов, принадлежащих линейному пространству W, называется совокупность всех линейных комбинаций этих векторов

Свойства линейной оболочки
1) Линейная оболочка содержит само множество X.
2) Если линейное пространство W содержит множество X, то:
а) пространство W содержит и его линейную оболочку L(X);
б) L(X) ‒ линейное подпространство пространства W.
Пример: Найти линейную оболочку множества решений системы уравнений:

Решение: Ранг матрицы коэффициентов системы уравнений равен 2. Выберем свободными переменными х2 и х4. Тогда общее решение однородной системы уравнений имеет вид

где c1 , c2 ϵ R .
Векторы £ = (‒1, 1, 0, 0) и η = (1, 0, ‒1, 1) образуют фундаментальный набор решений однородной системы. Любое решение системы является их линейной комбинацией. Значит, линейная оболочка векторов £ и η является множеством решений однородной системы уравнений,
т.е.
L(£,η)
=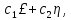 где
где ,
,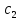 ϵR
.
ϵR
.
