Дискретна математика

На прикладі 2.4 легко помітити, зокрема, що розрізу {e3, e6, e7} у графі G відповідає цикл f 1, e 3,f 2, e 6, f 4, e 7, f 1 у графі Gg. Цей результат узагальнює наступна

Теорема 3.32. Множина ребер планарного графа G утворює цикл у G тоді і тільки тоді, коли відповідні їм ребра утворюють розріз у геометрично двоїстому йому графі Gg.

Доведення.

Наслідок 3.3. Множина ребер планарного графа G утворить розріз у G тоді і тільки тоді, коли відповідні їм ребра утворять цикл у Gg і навпаки.

Теорема 3.33. Граф G є планарним тоді і тільки тоді, коли він має двоїстий.

Цей результат можна використовувати завжди, коли зручніше дослідження планарності графів замінити дослідженням циклів графа і розрізів двоїстого графа і навпаки.

62.Оцінки х р ктеристик гр фів.

Розглянемо деякі оцінки для графів, визначених іншим шляхом. Нижче число ребер і число компонентів графа G позначаються через m(G) і k(G) відповідно.

Очевидно, що число ребер у довільному графі порядку n не більше числа ребер у Кn, рівного (n(n – 1))/2. Але скільки ребер може бути в графі порядку n з фіксованим числом k компонент? На це питання відповідає наступна

Теорема 3.34. Якщо k(G) = k для n-вершинного графа G, то n-k ≤ m (G) ≤ (n-k)(n-k+ 1)/2, (*)

причому обидві ці оцінки для m(G) досяжні.

Доведення. Спочатку розглянемо верхню оцінку. Нехай G - граф порядку n з k компонентами і максимальним для таких графів числом ребер. Тоді кожен його компонент є повним графом. Нехай, далі, Кр і Kq - дві компоненти, р ≥ q > 1, v - вершина з другої компоненти. Видаливши з графа всі ребра, інцидентні вершині v, і з'єднавши v ребром з кожною вершиною з першої компоненти, одержимо новий граф порядку n з тим же числом компонентів і більшим числом ребер. Останнє неможливе, отже тільки один з компонентів може мати порядок, більший 1. Він дорівнює n-k+1, а тому

m(G) = (n - k)(n-k+1)/2.

Справедливість верхньої оцінки (*) і її досяжність доведені.

Перейдемо до доведення нерівності m(G) ≥n-k. Воно очевидне при m(G) = 0, тому що тоді k = п. Скористаємося індукцією по m(G). Нехай m(G) > 0 і нехай для графів з меншим, чим m(G) числом ребер відповідна нерівність вірна. Розглянемо граф G - е, де е EG. Відповідно до теореми 3.9 число компонент цього графа дорівнює k чи k + 1. Число ребер у ньому дорівнює m(G)–1. За індуктивним припущенням в обох випадках m(G) - 1 ≥ n-k-1. Отже, m(G) ≥ n-k. Потрібна нерівність доведена.

Диз‘юнктивне об'єднання G = Ok-1 Kn-h+1 реалізує рівність m(G) = n - k. Теорема доведена.

З першої частини приведеного доведення випливає

Наслідок 3.4. При фіксованих n і k ≤ n серед графів G порядку n з k(G)= k існує тільки один граф, а саме, G = Ok-1 Kn-h+1, з максимальним числом ребер.

Існує доведене твердження, що на n вершинах можна побудувати nn-2 різних дерева.

63.Теорем Ейлер .

Теорема 3.35 (Теорема Эйлера). Для зв'язного плоского графа G справедлива умова n + g = m + 2, де n - число вершин, m - число ребер, g - число граней графа G.

Доведення. Індукцією по числу ребер. Нехай m = 0, тоді n = 1 (тому що G - зв'язний) і існує одна нескінченна грань. У такий спосіб n+g = m+2.

Індуктивне припущення – твердження вірне для числа ребер m-1.

Додамо ребро. Якщо це петля, то додасться грань. Якщо це ребро між існуючими вершинами, то одна з граней, тому що граф зв'язний, розщеплюється на дві. Якщо ребро інцидентне одній вершині, то нових граней немає, але потрібно додати ще одну вершину. Тому що інших ситуацій не виникає, а в кожній з розглянутих до рівності n+g = m+2 додається праворуч і ліворуч по одиниці, то теорема виконується.

Теорема доведена.

Варіантом теореми Ейлера для незв'язних графів є наступна

Теорема 3.36. Якщо граф G - плоский з n вершинами, m ребрами, f гранями, k компонентами, то n+f=m+k+1.

Доведення. Кожну компоненту оцінюємо за теоремою Ейлера і підсумовуємо ліві і праві частини, причому нескінченну грань для кожної компонента порахуємо один раз. Теорема доведена.

Дуже в жлив для н с н ступн

Теорема 3.37. Якщо G - зв'язний простий планарний граф з n ≥ 3 вершинами і m ребрами, то m ≤ 3n-6. Доведення. Справедливо 3f ≤ 2m (тому що для грані потрібно мінімум 3 ребра, а може і більше, а

кожне ребро бере участь в утворенні 2 граней). А тоді за теоремою Ейлера одержуємо 3(-n+m+2) ≤ 2m чи m ≤ 3n-6, що і потрібно було довести. Теорема доведена

71

І ще одного потрібний для розф рбув ння гр фів результ т д є н ступн

Теорема 3.38. У будь-якому простому планарному графі існує вершина, ступінь якої не більше 5. Доведення. Нехай ступінь кожної вершини не менше 6. Тоді 6n ≤ 2m чи 3n ≤ m. Але з попередньої

теореми відразу ж випливає 3n ≤ 3n-6. Отримане протиріччя вимагає відмовитися від припущення. Теорема доведена.

64.Розф рбув ння гр фів.

1. Пост новк проблеми. З проблемою розфарбування графа пов'язане поняття його хроматичного числа. Нехай заданий граф G без петель.

Визначення. Граф G називається k-розфарбовуваним, якщо можна задати усюди визначену функцію f: V K, |K| = k таку, що для будь-яких двох його суміжних вершин v і u виконується умова f(v) f(u).

Множина K – множина кольорів. Якщо для вершин v і u виконується умова f(v) = f(u), то говорять, що вони мають один колір. Власне сама множина K нас не цікавить. Для визначеності звичайно приймаетя, що K – підмножина N.

Очевидно, якщо гр ф G k-розф рбовув ний, то він і k+1-розф рбовув ний. Обернене в з г льному вип дку не вірне.

Визначення. Якщо граф G – k-розфарбовуваний, але не k-1-розфарбовуваний, то він називається k- хромататичним, а число k - хромататичним числом графа G.

Існує ще один варіант розфарбування – реберне розфарбування.

Визначення. Граф G називається реберно k-розфарбовуваним, якщо можна задати усюди визначену функцію f: E K, |K| = k таку, що для будь-яких двох його ребер e і q, інцидентних одній і тій же вершині, виконується умова f(e) f(q).

Розглянемо розфарбування вершин простих графів, тому що петлі роблять безглуздим розфарбування графа, а паралельність ребер не впливає на результат. Існують часткові та загальні результати про розфарбування графів.

2.З г льні результ ти. Спочатку розглянемо результати щодо розфарбування графыв довільного

вигляду.

Теорема 3.40. Якщо G – граф, максимальний ступінь вершин якого дорівнює p, то граф G (p+1)- розфарбовуваний.

Доведення. Індукцією по числу вершин. Нехай n вершин. Якщо видалити одну, то граф з n-1 вершинами буде p розфарбовуваним. Вилучена вершина суміжна з ≤ p вершинами, отже їй потрібний p+1-й колір.

Теорема 3.41 (теорема Брукса). Нехай G – граф, максимальний ступінь вершин якого дорівнює p.

Тоді G p-розфарбовуваний за винятком випадків, коли (1) G містить як компонент повний граф Kp+1 чи (2) при p = 2 і цикл непарної довжини є компонентом G.

Більш вагомі результати для окремих класів графів.

3.Розф рбув ння пл н рных гр фів. Оскільки планарны графи становлять дуже важливий клас графывЮ розглянемо особливості ъх розфарбування.

Теорема 3.42. Будь-який планарний граф 6 –розфарбовуваний. Теорема 3.43. Будь-який планарний граф 5 – розфарбовуваний. Теорема 3.44. Будь-який планарний граф 4 – розфарбовуваний.

Ми доведемо тільки другу з цих теорем. Застосуємо індукцію по числу вершин. Нехай G з n-1 вершиною 5-розфарбовуваний.

Додамо 1 вершину v, тоді ступінь її по теоремі 3.38 не більш 5. Можливі наступні випадки:

1.d(v) < 5. Тоді вершині v даємо колір, що не використовується суміжними вершинами – очевидно він є і теорема доведена.

2.d(v) > 5. Але суміжні вершини, скажімо vi і vj використовують той же колір. Тоді відсутній колір беремо для v і теорема доведена.

3.d(v) = 5. Вершина v суміжна, скажімо v1,…,v5, кожна з яких має окремий колір, нехай 1,…,5 відповідно. Нехай Vij подграф G такий, что: а) Vij включає усі вершини, що мають колір i чи j; б) ребра включаються всі ті, які утворять шлях між vi і vj.

Тепер для v1 і v3 є 2 можливості:

а) v1 і v3 не належать V13. Тоді для v1 можна взяти колір вершини v3 і колір, що залишився, можна використовувати для v;

б) v1 і v3 належать V13. Але тоді v2 і v4 повинні бути в різних компонентах V24 і те ж можна проробити для кольорів 2 і 4 вершин v2 і v4. Теорема доведена.

65.Теорем Хол про весілля

Теорема про весілля пов'язана з рішенням задачі про весілля: задана скінчена множина юнаків, кожний з який знайомий з декількома дівчатами; запитується, за яких умов можна одружити юнаків так, щоб кожний з них женився на знайомій йому дівчині? (вважаємо, что полігамія не дозволена). Наприклад,

72

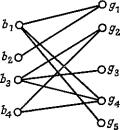
якщо є четверо юнаків { b1 , b2 , b3 , b4 } і п'ять дівчат { g1 , g2 , g3 , g4 , g5 }, а відношення знайомства між ними вказані в наступній таблиці:

то можливе таке рішення: b1 жениться на g4, b2 — на g1, b3 — на g3, а b4 — на g2.

Цю задачу можна представити графічно, використовуючи двочастковий граф G з множиною вершин, розбитою на дві підмножини V1 і V2 (зображують юнаків і дівчат відповідно), і множиною ребер, кожне з який відповідає знайомій парі (юнак, дівчина). Граф для нашого прикладу має наступний вигляд:

Визначення. Вершинним паросполученням з V1 в V2 у двочастковому графі G з частками, визначеними на підмножинах V1,V2, назвемо взаємно однозначну відповідність між вершинами з підмножини V1 і підмножиною вершин з V2, яка має ту властивість, що відповідні вершини з'єднані ребром.

Зрозуміло, що задачу про весілля можна виразити в термінах теорії графів у такий спосіб: якщо G - двочастковий граф з частками, визначеними на підмножинах V1,V2, то за яких умов у G існує вершинне

паросполучення з V1 у V2.

Використовуючи запропоновану термінологію, можна сформулювати наступне очевидне твердження: необхідна умова для існування рішення в задачі про весілля полягає в тому, що будь-які k юнаки з даної множини повинні бути знайомі (у сукупності) щонайменше з k дівчатами (для всіх цілих k, що задовольняють нерівностям 1 k m, де через m позначене загальне число юнаків).

Необхідність цієї умови відразу випливає з того, що якщо вона не вірна для якої-небудь множини з k юнаками, то ми не зможемо женити необхідним способом навіть цих k юнаків, не говорячи уже про інших. Вражає те, що ця очевидна необхідна умова є в той же час і достатньою. У цьому і полягає теорема Хола про весілля.

Теорема 3.45. Рішення задачі про весілля існує тоді і тільки тоді, коли будь-які k юнаки з даної множини знайомі в сукупності щонайменше з k дівчатами (1 k m).

Доведення (Халмоша і Вогена). Як було відзначено вище, необхідність умови очевидна. Для доведення достатності скористаємося індукцією. Очевидно, що при m = 1 теорема вірна. Допустимо, що твердження справедливе, якщо число юнаків менше m. Припустимо тепер, що число юнаків дорівнює m, і розглянемо два можливих випадки.

1.Будемо вважати, що будь-які k юнаків (1 k m) у сукупності знайомі щонайменше з k + 1 дівчатами (наша умова завжди виконується «з однією зайвою дівчиною»). Тоді, якщо взяти будь-якого юнака і женити його на будь-якій знайомій йому дівчині, для інших m - 1 юнаків залишиться вірним первісна умова. За припущенням індукції ми можемо женити цих m - 1 юнаків. Тим самим доведення у першому випадку завершено.

2.Припустимо, що маємо k юнаків (k<m), що у сукупності знайомі рівно з k дівчатами. За

припущенням індукції цих k юнаків можна женити. Залишаються ще m - k юнаків, але будь-які h з них (1 hm - k) повинні бути знайомі щонайменше з h дівчатами що залишилися, оскільки в супротивному випадку ці h юнаків разом із вже обраними k юнаками будуть знайомі менше, ніж з h + k дівчатами, а це суперечить нашому припущенню. Отже, для цих m - k юнаків виконана первісна умова, і за припущенням індукції ми можемо їх женити так, щоб кожний був щасливий. Теорема доведена.

Теорему можна також сформулювати мовою паросполучень у двочастковому графі.

Наслідок 3.5. Нехай G - двочастковий граф з частками, визначеними на підмножинах V1,V2, і для будь-якої підмножини А множини V1 нехай (А) – множина тих вершин з V2, що суміжні принаймні з однією вершиною А. Тоді вершинне паросполучення з V1 у V2 існує в тому і тільки в тому випадку, якщо |A|| (А)| для кожної підмножини А з V1.

73

Доведення. Доведення цього наслідку є просто перекладом викладеного вище доведення на мову теорії графів.

66.Теорія тр нсверс лей

Розглянемо ще одне доведення теореми Хола, що використовує мову теорії трансверсалей. Визначення. Якщо E — непорожня скінчена множина і S = (S1, ..., Sm) – сім‘я (не обов'язково різних)

непорожніх її підмножин, трансверсаллю (чи системою різних представників) для S назвемо підмножину множини Е, що складається з m різних елементів: по одному з кожної підмножини Si.

Приклад 31. Нехай Е = {1, 2, 3, 4, 5, 6}, a S1 = S2 = {1, 2}, S3 = S4 = {2, 3}, S5 = {1, 4, 5, 6}. Тут неможливо знайти п'ять різних елементів з E - по одному з кожної підмножини Si, іншими словами, ця сім‘я S = (S1, ..., S5) не має трансверсалі. Помітимо, однак, що його підродина S'= (S1,S2,S3,S5) має трансверсаль,

наприклад {1, 2, 3, 4}.

Визначення. Трансверсаль довільної підродини сім‘ї S будемо називати частковою трансверсаллю

для S.

У нашому прикладі сім‘я S має декілька часткових трансверсалей (наприклад, {1, 2, 3, 6}, {2, 3, 6}, {1, 5}, Ø і т.д.). Зрозуміло, що будь-яка підмножина часткової трансверсалі сама є частковою

трансверсаллю.

За яких умов дана сім‘я підмножин деякої множини має трансверсаль? Легко побачити зв'язок між цією задачею і задачею про весілля, якщо взяти за Е множину дівчат, а за Si - множину дівчат, знайомих юнаку bi, (1 i m). Трансверсаллю в цьому випадку є множина з m дівчат, така, що кожному юнакові відповідає рівно одна (знайома йому) дівчина. Отже, теорема Хола дає необхідну і достатню умову існування трансверсалі для даної сім‘ї множин. Сформулюємо теорему Хола для цього випадку.

Теорема 3.46. Нехай Е – непорожня скінченна множина і S = (S1,…,Sm) – сім‘я непорожніх її підмножин. Тоді S має трансверсаль у тому і тільки в тому випадку, якщо для будь-яких k підмножин Si їх об'єднання містить щонайменше k елементів (1 k m).

Доведення (Р.Радий). Необхідність цієї умови очевидна. Для доведення достатності установимо, що якщо одна з підмножин (скажімо, S1) містить більш одного елемента, то можна видалити один елемент із S1, не порушивши умови теореми. Повторенням цієї процедури ми доб‘ємося зведення задачі до того випадку, коли кожна підмножина містить тільки один елемент. Тоді твердження стане очевидним.

Залишилося обґрунтувати законність цієї «процедури зведення». Припустимо, що S1 містить елементи x і y, вилучення кожного з яких порушує умову теореми. Тоді існують підмножини А и В множини {2, 3, …, m}, яку мають ту властивість, що

Наслідок 3.6. У тих же позначеннях, що і вище, S має часткову трансверсаль потужності t тоді і тільки тоді, коли для будь-яких k підмножин Si їх об'єднання містить щонайменше k + t - m елементів.

Доведення. Необхідний результат можна одержати, застосувавши теорему 3.46 до сім‘ї S' =

S1 D, , Sm D , де D - довільна множина, що не перетинається з множиною Е і складається з m - t

елементів. Зазначимо, що S має часткову трансверсаль потужності t тоді і тільки тоді, коли S' має трансверсаль.

Наслідок 3.7. Якщо. Е і S такі ж, як і раніше, а Х - будь-яка підмножина з Е, то Х містить часткову трансверсаль потужності t для S тоді і тільки тоді, коли для кожної підмножини А множини {1, ..., т}

( S j ) X A t m

j A

Доведення. Досить застосувати попередній наслідок до сім‘ї Sx= (S1 X , , Sm X ) .

3. Застосування теореми Хола. Розглянемо деякі важливі застосування теореми Хола.

74

3.1). Латинські квадрати. Латинським (m n)-прямокутником називається матриця M = (mij)

розмірністю (m n), елементами якої є цілі числа, що задовольняють умовам: (1) 1 mij n; (2) всі елементи в кожнім рядку й у кожнім стовпці різні. Помітимо, що з умов (1) і (2) випливає, що m n. Якщо m = n, то латинський прямокутник називається латинським квадратом.

Приклади латинського (3 5)-прямокутники і латинського (5 5)-квадрата наведені на рис.3.11 і 3.12 відповідно.

Рис. 3.11 Рис. 3.12

Питання: коли до латинського (m n)-прямокутника, де m < n, можна приєднати n - m нових рядків так, щоб вийшов латинський квадрат? Відповідь на це питання дає наступна

Теорема 3.47. Будь-який латинський (n m)-прямокутник М, де m<n, можна розширити до латинського квадрата додаванням n-m нових рядків.

Доведення. Покажемо, що М можна розширити до латинського (m+1) n- прямокутника. Повтор цієї процедури приведе до латинського квадрата.

Нехай Е = {1, 2, ...,n} і S = (S1, ...,Sn ), де через Si позначена множина, що складається з тих елементів множини Е, що не зустрічаються в i-м стовпці матриці М. Якщо ми зможемо довести, що S має трансверсаль, то тим самим ми доведемо теорему, оскільки елементи цієї трансверсалі й утворять додатковий рядок. По теоремі Хола досить довести, що об'єднання будь-яких k підмножин Si містить щонайменше k різних елементів. А це очевидно, тому що будь-яке таке об'єднання містить (n - m)k елементів (включаючи повторення), і якби в ньому було менш k різних елементів, то принаймні один з них повторювався б більш ніж n - m разів, що неможливо.

67.Теорем Менгер

Тут ми обговоримо одну теорему, тісно пов'язану з теоремою Хола, що має широке практичне застосування. Ця теорема, що належить Менгеру, стосується числа простих ланцюгів, що з'єднують дві дані вершини

Рис. 3.13.

v і w графа G. Приміром, нас може цікавити, яке максимальне число простих ланцюгів з v у w, ніякі два з яких не мають спільного ребра, — такі прості ланцюги називаються реберно непересічними. Чи може виникнути інше питання: яке максимальне число простих ланцюгів з v у w, ніякі два з яких не мають загальної вершини (крім, зрозуміло, v і w), — такі ланцюги називаються вершинно непересічними. (Так, у графі, зображеному на рис.3.13, є чотири реберно непересічні і два вершинно непересічні прості ланцюги з v у w.) Аналогічно, можна запитати, чому рівняється максимальне число вершинно непересічних чи непересічних по дугах простих орланцюгів (визначених очевидним чином), що з'єднують дві вершини v і w деякого орграфа. У цьому випадку ми можемо, не втрачаючи загальності, вважати v витоком, а w — стоком. В основному ми будемо мати справу з графами, але результати легко поширити на орграфи.

Для цього нам знадобиться ще декілька означень; усюди тут будемо вважати, що G — зв'язний граф, а v і w — дві різні його вершини.

Назвемо vw-поділяючою множиною в G множину Е ребер графа G, який має ту властивість, що будь-який простий ланцюг з v у w містить ребро з Е; помітимо, що всяка vw- поділяюча множина є і поділяючою множиною в G. Аналогічно, що vw-відокремлюючою множиною в G назвемо множину S його вершин (не містить v і w), що має ту властивість, що будь-який простий ланцюг з v у w проходить через вершину з S. Наприклад, на мал. 3.13 множини E1 = {{р, s}, {q, s}, {t, у}, {t, z}} і E2 = {{u, w)}, {х, w}, {у, w}, {z, w}} є vw-поділяючими, а множини V1 = {s, t} і V2 = {р, q, y, z} є vw-відокремлюючими.

Для того щоб підрахувати число реберно непересічних простих ланцюгів з v у w, помітимо спочатку, що якщо яка-небудь vw-поділяюча множина Е містить k ребер, то число реберно непересічних простих ланцюгів не перевищує k, оскільки в супротивному випадку деяке ребро з Е належало б більш ніж одному простому

75

ланцюгу. Якщо до того ж Е є множиною найменшої можливої, що поділяє, потужності, то число реберно непересічних простих ланцюгів виявляється в точності рівним цій потужності і, отже, кожен такий ланцюг містить рівно одне ребро з E. Цей результат відомий як реберна форма теореми Менгера, хоча в дійсності він був уперше доведений Фордом і Фалкерсоном у 1955 р.

Теорема 3.51. Максимальне число реберно непересічних простих ланцюгів, що з'єднують дві різні вершини v і w зв‘язного графа G, дорівнює мінімальному числу k ребер у vw-поділяючій множині.

Зауваження. Доведення, що ми збираємося запропонувати, не є конструктивним у тому сенсі, що воно не дає ні способу одержання k реберно непересічних простих ланцюгів для заданого графа G, ні навіть способу визначення величини k. Алгоритм, що дозволяє вирішити ці задачі, буде описаний у наступній темі.

Доведення. Як ми встановили вище, максимальне число реберно непересічних простих ланцюгів, що з'єднують v і w, не перевищує мінімального числа ребер vw-поділяючої множини. Щоб довести, що ці числа рівні, скористаємося індукцією по числу ребер у G. Припустимо, що G містить m ребер і що теорема вірна для всіх графів, у яких число ребер менше ніж m. Розглянемо два можливих випадки.

(I) Припустимо, що існує vw-поділяюча множина Е мінімальної потужності k, що володіє такою властивістю, що не всі її ребра інцидентні v і не всі інцидентні w. Наприклад ,

Рис. 3.14.

у графі, зображеному на рис.3.14, такою vw-поділяючою множиною є множина E1 == {{р, s}, {q, s}, {t, у}, {t, z}}. Після видалення з G ребер, що належать Е, залишаються два непересічних підграфа V і W, що містять відповідно v і w. Визначимо тепер два нових графи G1 і G2: G1 отримується з G стягуванням кожного ребра з V (тобто стисканням V до v), a G2 отримується аналогічним стягуванням кожного ребра з W. (Графи G1 і G2, отримані з графа, зображеного на рис.3.13, показані на рис.3.14; пунктирними лініями позначені ребра множини E1). Оскільки число ребер у G1 і G2 менше, ніж у G, і оскільки зрозуміло, що Е є vw-поділяючою множиною мінімальної потужності для обох графів G1 і G2, то по припущенню індукції в G1 існує k реберно непересічних простих ланцюгів з v у w, і те ж саме вірно для графа G2. Комбінуючи очевидним образом ці прості ланцюги, ми одержимо k потрібних реберно непересічних простих ланцюгів у G.

(II) Тепер припустимо, що кожна vw-поділяюча множина мінімальної потужності k складається або з таких ребер, кожне з яких інцидентне v, або тільки з ребер, інцидентних вершині w. Такою vw-поділяючою множиною на мал. 3.13 є, наприклад, множина E2. Без утрати загальності можна вважати, що кожне ребро графа G міститься в деякій vw-поділяючий множині потужності k, тому що в супротивному випадку видалення відповідного ребра не вплине на величину k і дозволить нам скористатися індуктивним припущенням, щоб одержати k реберно непересічних простих ланцюгів. Отже, будь-який простий ланцюг С з v у w повинна складатися або з єдиного ребра, або з двох ребер, і тому може містити не більше одного ребра з будь-якої vw-поділяючої множини потужності k. Видаляючи з G ребра, що належать С, ми одержимо граф, що містить принаймні k — 1 реберно непересічних простих ланцюгів (по індуктивному припущенню). Разом з C ці прості ланцюги і дають потрібні k простих ланцюгів у G.

Звернемося тепер до іншої задачі, згаданої раніше: до визначення числа вершинно непересічних простих ланцюгів з v у w. На перший погляд здається дивним, що не тільки рішення цієї задачі має вигляд, подібний до теореми 3.51, але і саме доведення теореми 3.51 потребує незначних змін, що складаються головним чином у заміні таких термінів, як «реберно непересічний» і «інцидентний», на терміни «вершинно непересічний» і «суміжний». Сформулюємо тепер вершинну форму теореми Менгера.

Теорема 3.52 (теорема Менгера). Максимальне число вершинно непересічних простих ланцюгів, що з'єднують дві різні несуміжні вершини v і w графа G, дорівнює мінімальному числу вершин vwвідокремяюючої множини.

68.Ан лог теореми Менгер для оргр фів

Теорема 3.53. (теорема про цілочисельність). Максимальне число реберно непересічних простих орланцюгів, що з'єднуюють дві різні вершини v і w орграфа D, дорівнює мінімальному числу ребер vwподіляючоъї множини.

76

Нагадаємо, що мови програмування Паскаль, С, задовольняють цьому визначенню, якщо вважати словом програму. Природна мова також задовольняє визначенню, якщо вважати словом речення. Наведемо приклади мов в алфавіті Е = {0,1}, визначивши вигляд слів, що їм належать:

L1 = { ,0,1,01,10};

L2 = {0,00,000,...};

L3 = {1,11,111,...}; L4 = {0,1};

L5 = { };

L6 = ;

L7 = Е* = { , 0,1,00,1,01,10,000,001,010,100,011,101,110,111,...}.

Нагадаємо, що мова Е* містить всі слова в алфавіті Е, включаючи символи самого алфавіту Е. Тоді будь-яка мова в алфавіті Е є підмножиною Е*. Так, легко встановити, що L1 E*, L2 E*, L3 E*.

Над визначеними таким чином мовами також можна виконувати відомі нам теоретико-множинні операції над множинами, визначаючи об'єднання, перетин, різницю і доповнення мов. Варто зазначити, що для доповнення універсальною мовою виступає мова Е*. Крім того, будемо використовувати низку вже відомих нам важливих операцій, які ніколи не завадить повторити.

Означення. Нехай L1 - мова в алфавіті Е, L2 - мова в алфавіті Е2. Тоді мову{ L1 і L2} назвемо конкатенацією мов L1 і L2 і позначимо L1L2.

Приклад. L1L4={ | L1 і E2}={0,1,00,01,10,11,010,011,100,101. ..}.

Легко встановити, що конкатенація мов є операцією не комутативною, але асоціативною.

Означення. Нехай L - мова в алфавіті Е. Назвемо мову L* ітерацією мови L і визначимо таким чином:

L0 = {ε}

Ln = LLn-1 (n≥1)

вигляді Ln , то отриману мову назвемо позитивною ітерацією мови L і позначимо L+.

n 1

70.Визн чення гр м тик

Генератори типу граматик для породження мов виникли взагалі внаслідок спроби використати методи математики при дослідженні природних мов. Вирішальний внесок в їх розвиток внесли дослідницькі колективи, очолювані нині відомими всьому світові Н.Хомським і І.Бар-Хілелом. Однак, в сфері інформатики, управління і обробки даних широке дослідження і застосування граматик почалося з моменту виявлення того факту, що алгоритмічні мови типу Алгол породжені граматиками.

Означення. Назвемо граматикою систему <D, Е, Р, d0>, де:

D - скінчений алфавіт, що містить нетермінальні символи (інші назви: нетермінали, допоміжні символи, синтаксичні змінні);

Е - скінчений алфавіт, що містить термінальні символи (інша назва: термінали), причому D Е = ; P - скінченна множина правил виведення (інші назви: продукції, правила підстановки, правила

породження), що мають вигляд: , де , - слова в алфавіті D E, причому містить щонайменше один символ із алфавіту D;

d0 є D - початковий символ (інша назва: вихідний символ). Приклад:

Граматика G1 = <{d0, d1}{0,1}, Р, d0>, де Р містить наступні правила:

d0 0d11

0d1 00d11 d1

Тут 0 і 1 - термінальні символи, d0 і d1 - нетермінальні символи, причому d0 - початковий символ. Граматика визначає мову наступним чином. Будемо говорити, що слово безпосередньо породжує

слово або слово безпосередньо виводиться із слова в граматиці G, якщо = і = , де і - довільні слова в алфавіті D E і в граматиці G є правило виведення . Будемо позначати цей факт:

Якщо з контексту зрозуміло про яку граматику йде мова, то нижній індекс G можна не записувати. Природно, якщо , то .

78

(3)d2d1 d1d2

(4)1d1 11

(5)1d2 10

(6)0d2 00

Легко пересвідчитись, що ця граматика породжує мову

L(G1) = {010, 001100, 000 111 000,…}.

Необхідно підкреслити, що правило (3) наведеної в попередньому прикладі граматики G1 суперечить обмеженням на правила контекстно-залежних граматик, тобто G1 - це граматика без обмежень. Використовуючи додатковий нетермінал d3, легко замінити правило вигляду (3) декількома правилами, які не суперечать вимогам контекстно-залежних граматик, наступним чином:

(7)d2d1→d2d3

(8)d2d3→d1d3

(9)d1d3→d1d2

Якщо взяти правила (1), (2), (4) - (9), то отримаємо контекстно-залежну граматику G2, що породжує ту ж мову

L(G2) = {010,001100,000111000,…}.

73.Автом тні гр м тики

Правила виведення мають вигляд:

di dj або di , де di, dj D, - слово в алфавіті Е.

Приклад. Автоматною є граматика G4 = <{d0, d1}, {0,1}, Р, d0>, де множина Р містить такі правила:

d0 0d0

d0 1d0 d0

Легко перевірити, що ця граматика породжує мову {0,1}*.

Приклад. Маємо граматику G3 = <{d0, d1},{0,1}, Р, d0>, де множина Р містить правила:

d0 0d0

d0 1

Легко перевірити, що ця граматика породжує мову, слова якої мають вигляд:

{0000...01}

n

де n 0.

Іноді вимагається для граматик цього типу, щоб слово в алфавіті Е мало дожину, не більшу ніж 1. У зв‘язку з тим, що будь-яке слово в алфавіті Е може бути побудоване з правил автоматних граматик з урахуванням обмеження, кожну автоматну граматику можна замінити на автоматну граматику з зазначеним обмеженням, що породжує ту ж мову. З іншого боку, автоматна граматика з зазначеним обмеженням уже є автоматною граматикою без обмеження. Таким чином, ці два визначення еквівалентні, оскільки визначають ту ж множину регулярних мов.

74.Інші моделі гр м тик

1. Трансформаційні граматики. Ці граматики поширені в лінгвістиці. З їх допомогою легко описати структуру значної множини речень природної мови шляхом трансформацій раніше породжених речень. Тобто на відміну від процесу породження по символьного слів, в трансформаційних граматиках виконуються перетворення вже сформованих термінальних слів.

2. Моделі граматик з обмеженнями на порядок правил. Граматики Хомского класифіковані по відношенню до вигляду правил виведення і називаються граматиками безпосередньо складових. На сьогодні в лінгвістиці використовують кілька інших моделей граматик. Одні з них включають правила виведення специфічного вигляду, інші накладають обмеження на порядок виконання правил тощо. Розглянемо дві часто вживані моделі таких граматик.

75.Прогр мні гр м тики

В них застосовуються обмеження на порядок виконання правил виведення. Означення. Програмною граматикою назвемо систему <D, E, M, P, d0>, де D, E, P, d0

мають той же зміст, що і для граматик Хомського, а М - множина позначок правил виведення. Кожне правило з множини Р має вигляд:

(m) α β Y N, де m - позначка, m М, α, β - слова з множини (D E)* причому α містить хоча б один символ із алвавіту D; Y та N - підмножини M; α → β - ядро правила.

Функціонування програмної граматики опишемо наступним чином. Спочатку застосовується правило з позначкою (1). Далі для кожного правила з позначкою (m), якщо воно має вигляд α → β і в слові,

80