
Дискретна математика
.pdf
заперечення. Залишається тільки пересвідчитися у тому, що виконуються відносно кон`юнкції, диз`юнкції та заперечення всі вісім груп властивостей булевої алгебри.
Для цього остаточно визначимося з виділеними елементами. Очевидно, що замість виділеного елемента 0 (роль якого в алгебрі Кантора відіграє порожня множина ) варто перевірити абсолютно хибне висловлювання F (так ми назвемо заперечення абсолютно істинного висловлювання), а замість виділеного елемента 1 (роль якого в алгебрі Кантора відіграє універсальна множина U) є природним використати абсолютно істинне висловлювання Т.
Перевірка виконання властивостей булевих операцій відносно кон`юнкції, диз`юнкції та заперечення може бути реалізована за допомогою традиційного методу побудови таблиць істинності. Таблиці істинності для лівих і правих частин тотожностей, у формі яких подані властивості булевих операцій, повинні бути однаковими. Наприклад, що кон`юнкція комутативна і асоціативна засвідчують такі таблиці:
A |
|
B |
|
|
A B |
|
|
B A |
|
|
|
|
|
|
|
|
|||
F |
|
F |
|
|
F |
|
|
F |
|
|
|
|
|
|
|
|
|||
F |
|
T |
|
|
F |
|
|
F |
|
|
|
|
|
|
|
|
|||
T |
|
F |
|
|
F |
|
|
F |
|
|
|
|
|
|
|
|
|||
T |
|
T |
|
|
T |
|
|
T |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
B |
|
|
C |
|
|
(A B) C |
|
|
A (B C) |
|
|
|
|
|||
F |
|
|
F |
|
|
F |
|
|
F |
|
|
F |
|
|
|
|
|||
F |
|
|
F |
|
|
T |
|
|
F |
|
|
F |
|
|
|
|
|||
F |
|
|
T |
|
|
F |
|
|
F |
|
|
F |
|
|
|
|
|||
F |
|
|
T |
|
|
T |
|
|
F |
|
|
F |
|
|
|
|
|||
T |
|
|
F |
|
|
F |
|
|
F |
|
|
F |
|
|
|
|
|||
T |
|
|
F |
|
|
T |
|
|
F |
|
|
F |
|
|
|
|
|||
T |
|
|
T |
|
|
F |
|
|
F |
|
|
F |
|
|
|
|
|||
T |
|
|
T |
|
|
T |
|
|
T |
|
|
T |
|
|
|
|
|||
|
|
Перевірку всіх інших властивостей залишаємо читачеві. |
|
|
|
|
|
|
|||||||||||
|
|
Тепер залишається вирішити питання з кількістю операцій. Ми визначили множину R за |
|
|
|||||||||||||||
допомогою операцій ~, , , , . Сигнатура булевої алгебри вміщує лише три операції, яким ми |
|
||||||||||||||||||
співставили , , |
. Залишаються операції ~, , які не використовує булева алгебра, але за допомогою |
||||||||||||||||||
яких визначена множина R. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
У зв`язку з тим, що висловлювання, як ми вже казали, повністю визначаються своїми таблицями |
|||||||||||||||||
істинності, ми можемо всі висловлювання, утворені за допомогою зв`язок ~, , , , |
, замінити |
|
|||||||||||||||||
висловлюваннями, які утворені за допомогою лише зв`язок , , |
, але мають ту ж таблицю істинності. |
||||||||||||||||||
Таким чином, для побудови множини висловлювань R ми можемо обмежитися лише зв`язками , , . |
|||||||||||||||||||
Якщо ж виникає потреба аналізувати за допомогою алгебраїчних засобів висловлювання, яке містить |
|
||||||||||||||||||
зв`язки ~, , то його спочатку треба виразити у вигляді висловлювання, яке містить лише зв`язки , |
, |
||||||||||||||||||
|
. Для цього можна використовувати заміну висловлювань А ~ В, А В на висловлювання ( |
А |
В) |
||||||||||||||||
( А В), |
А В, відповідно. Тотожність таких перетворень засвідчують таблиці: |
|
|
|
|
||||||||||||||
|
|
А |
|
|
|
|
В |
|
А В |
|
А В |
|
|
||||||
|
|
F |
|
|
|
|
F |
|
|
T |
|
|
T |
|
|
||||
|
|
F |
|
|
|
|
T |
|
|
T |
|
|
T |
|
|
||||
|
|
T |
|
|
|
|
F |
|
|
F |
|
|
F |
|
|
||||
|
|
T |
|
|
|
|
T |
|
|
T |
|
|
T |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
A |
|
|
|
|
B |
|
А ~ В |
|
( А |
В) (А В) |
|
||||||
|
|
F |
|
|
|
|
F |
|
|
T |
|
|
T |
|
|
||||
|
|
F |
|
|
|
|
T |
|
|
F |
|
|
F |
|
|
||||
|
|
T |
|
|
|
|
F |
|
|
F |
|
|
F |
|
|
||||
|
|
T |
|
|
|
|
T |
|
|
T |
|
|
T |
|
|
||||
|
|
Отже, розглянемо алгебраїчну систему <R, , , |
, F, T>, де , - дві бінарні булеві операції |
|
|||||||||||||||
кон`юнкція і диз`юнкція, - унарна булева операція заперечення, F, T - виділені елементи, а відносно |
|||||||||||||||||||
операцій та виділених елементів виконуються такі властивості: |
|
|
|
|
|
|
|||||||||||||
|
|
1) ідемпотентність: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
А А = А, |
|
|
|
|
|
|
|
|
А А = А; |
|
|
|
|
||||
|
|
2) комутативність: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
А В = В А, |
|
|
|
|
|
А В = В А; |
|
|
|
|
|||||||
3) асоціативність:
131

( А В ) С = А ( В С ), |
( А В ) С = А ( В С ); |
|
4) |
дистрибутивність: |
|
А ( В С ) = ( А В ) ( А С ), |
А ( В С ) = ( А В ) ( А С ); |
|
5) |
властивості виділенних елементів: |
|
A F = F, |
A F = A, |
|
A T = A, |
A T = T; |
|
6) |
властивості заперечення: |
|
A A = T, |
A A = F; |
|
7)властивість подвійного заперечення:
А= (
( А );
А );
8)правило де Моргана:
 ( А В ) =
( А В ) = А
А  В,
В,  ( А В ) =
( А В ) = А
А  В.
В.
Тепер ми можемо сказати, що побудували алгебраїчну систему, яка належить до булевих алгебр, носієм якої є множина висловлювань, а операціями - логічні кон`юнкція, диз`юнкція, заперечення, носій містить виділені елементи, відносно яких та логічних зв`язок виконуються всі властивості булевої алгебри. Ця базова алгебраїчна система називається булевою алгеброю висловлювань або алгеброю висловлювань. Таким чином, на алгебру висловлювань ми можемо поширити всі відомі результати, що стосуються булевих алгебр. Наприклад, відоме в булевих алгебрах правило поглинання x (x y) = x може бути використане в алгебрі висловлювань у вигляді A (A B) = A для того ж спрощення складних висловлювань.
Для поглиблення уявлень про тотожність висловлювань буде корисно пов`язати її з еквівалентністю.
Справедлива наступна Теорема 6.6. А = В тоді і тільки тоді, коли висловлювання А ~ В асолютно істинне.
Доведення.
Пряма теорема.
Нехай А = В. Тоді, за означенням тотожності, А і В мають однакові таблиці істинності. Звідси, за означенням зв`язки еквівалентність, висловлювання А ~ В буде істинним на всіх наборах значень істиності висловлювань А та В, тобто абсолютно істинним.
Обернена теорема доводиться аналогічно.
Теорема доведена.
При алгебраїчних перетвореннях можна використовувати також властивості відношення тотожності як відношення еквівалентності:
а) рефлексивність: А = А; б) симетричність: якщо А = В, то В = А;
в) транзитивність: якщо А = В і В = С, то А = С.
Отже, ми сформували алгебраїчну систему для висловлювань і тепер можемо використовувати алгебраїчний метод для вирішення проблем логіки.
112.Елемент рні кон'юнкція т диз'юнкція
Крім контрарних пар зручні особливості мають форми, які називаються елементарними кон`юнкціями і диз`юнкціями.
Означення. Елементарною диз`юнкцією (кон`юнкцією) будемо називати складне висловлювання, що має такий вигляд A1 A2 ... An (A1 A2 ... An), де Ai, i = 1,2, ... ,n є простим висловлюванням або його запереченням.
Якщо треба аналізувати висловлювання, яке не є висловлюванням зазначеного вище вигляду, то використовуючи алгебраїчні перетворення ми можемо здійснити спробу привести його до вигляду елементарної диз`юнкції або кон`юнкції. Елементарні диз`юнкція та кон`юнкція дуже зручні для встановлення абсолютної істинності (хибності) складних висловлювань. Критерії абсолютної істинності (хибності) встановлюють наступні
Теорема 6.7. Елементарна диз`юнкція абсолютно істинна тоді і тільки тоді, коли вона містить щонайменше пару висловлювань, з яких одне є запереченням іншого.
Доведення.
Прям теорем .
Нехай елементарна диз`юнкція містить таку пару: Ai, Ai. Якщо вони не стоять поруч, то ми можемо поставити їх поруч, скориставшись властивістю комутативності. Тепер, виходячи з властивостей заперечення та виділених елементів, за кілька кроків алгебраїчних перетворень отримаємо бажаний результат, тобто те, що елементарна диз`юнкція набуває значення Т.
Ai. Якщо вони не стоять поруч, то ми можемо поставити їх поруч, скориставшись властивістю комутативності. Тепер, виходячи з властивостей заперечення та виділених елементів, за кілька кроків алгебраїчних перетворень отримаємо бажаний результат, тобто те, що елементарна диз`юнкція набуває значення Т.
Обернен теорем .
Нехай елементарна диз`юнкція абсолютно істинна. Покажемо, що вона містить зазначену в умові теореми пару. Доведення поведемо від супротивного. Нехай це не так. Присвоїмо простим
132

висловлюванням без заперечення значення F, а простим висловлюванням із запереченням - значення T. За властивостями зв`язок заперечення і диз`юнкції, елементарна диз`юнкція набуде значення F, що протирічить умові. Звідси випливає, що для того, щоб елементарна диз`юнкція була істинною, необхідна наявність в ній пари висловлювань, з яких одне є запереченням іншого.
Теорема доведена.
Теорема 6.8. Елементарна кон`юнкція абсолютно хибна тоді і тільки тоді, коли вона містить щонайменше пару висловлювань, з яких одне є запереченням іншого.
Доведення.
Прям теорем .
Нехай елементарна кон`юнкція містить таку пару Ai, Ai. Якщо вони не стоять поруч, то ми можемо поставити їх поруч, скориставшись властивістю комутативності. Тепер, виходячи з властивостей заперечення та кон`юнкції алгебри висловлювань, за кілька кроків алгебраїчних перетворень отримаємо бажаний результат, тобто те, що елементарна кон`юнкція набуде значення F.
Ai. Якщо вони не стоять поруч, то ми можемо поставити їх поруч, скориставшись властивістю комутативності. Тепер, виходячи з властивостей заперечення та кон`юнкції алгебри висловлювань, за кілька кроків алгебраїчних перетворень отримаємо бажаний результат, тобто те, що елементарна кон`юнкція набуде значення F.
Обернен теорем .
Нехай елементарна кон`юнкція абсолютно хибна. Покажемо, що вона містить зазначену в умові теореми пару. Доведення поведемо від супротивного. Нехай це не так. Присвоїмо простим висловлюванням без заперечення значення T, а простим висловлюванням із заперечення - значення F. За властивостями зв`язок заперечення і кон`юнкції, елементарна кон`юнкція набуде значення T, що протирічить умові теореми. Виходячи з цього, робимо висновок, що для того, щоб елементарна кон`юнкція була абсолютно хибною необхідна наявність в ній зазначеної пари.
Теорема доведена.
Таким чином, якщо ми хочемо встановити абсолютну істинність (хибність) складного висловлювання, то за допомогою алгебраїчних перетворень треба привести його до вигляду елементарної диз`юнкції (кон`юнкції) і застосовати критерії із теорем 6.7 (6.8). Виявилося, що ми не можемо поступити таким чином з усіма складними висловлюваннями, тобто не кожне складне висловлювання можна виразити у вигляді елементарної диз`юнкції (кон`юнкції). Тому склад зручних форм висловлювань, користуючись якими ми можемо легко з`ясовувати абсолютну істинність (хибність) складного висловлювання, необхідно розширити. Перейдемо до використання форм, що утворені за допомогою всіх трьох операцій булевої алгебри висловлювань.
113.Диз'юнктивн і кон'юктивн норм льні форми
Нормальні форми широко використовуються всюди в дискретній математиці і зокрема в математичній логіці.
Означення. Диз`юнктивною нормальною формою (ДНФ) будемо називати диз`юнкцію
елементарних кон`юнкцій. |
|
Приклад. A1 A2 A2 A3 |
A1 A2 A3. |
Означення. Кон`юнктивною нормальною формою (КНФ) будемо називати кон`юнкцію |
|
елементарних диз`юнкцій. |
|
Приклад. (A1 A2 A3) (A2 |
A3 A2). |
Критерії встановлення абсолютної істинності та абсолютної хибності за допомогою ДНФ і КНФ формулюється у вигляді наступних
Теорема 6.9. Диз`юнктивна нормальна форма абсолютно хибна тоді і тільки тоді, коли кожна її елементарна кон`юнкція містить пару висловлювань, з яких одне є запереченням іншого.
Доведення.
Прям теорем .
Нехай умова виконується. Тоді, на підставі властивостей елементарної кон`юнкції (теорема 6.8.), кожна із елементарних кон`юнкцій, що входять до складу ДНФ, набуде значення F. Тоді, очевидно, і вся ДНФ набуде значення F згідно з означенням диз`юнкції.
Обернен теорем .
Нехай ДНФ абсолютно хибна. Покажемо, що повинна виконуватись умова теореми. Доведення поведемо від супротивного. Нехай умова теореми не виконується. Використовуючи прийом, який ми застосовували в доведенняі теорем 6.7 і 6.8, можемо побудувати такий набір значень істинності простих висловлювань, при якому ДНФ набуде значення T, що буде суперечити умові.
Теорема доведена.
Теорема 6.10. Кон`юнктивна нормальна форма абсолютно істинна тоді і тільки тоді, коли кожна її елементарна диз`юнкція містить пару висловлювань, з яких одне є запереченням іншого.
Доведення.
Прям теорем .
Нехай умова виконується. Тоді, на підставі властивостей елементарної диз`юнкції, кожна із елементарних диз`юнкцій, що входять до складу КНФ, набуде значення T. Тоді, очевидно, і вся КНФ набуде значення T згідно з означенням кон`юнкції.
133
Обернен теорем .
Нехай КНФ абсолютно істинна. Покажемо, що повинна виконуватися умова теореми. Доведення поведемо від супротивного. Нехай умова не виконується. Використовуючи прийом, який ми застосовували при доведенні теорем 6.7 і 6.8, можемо побудувати такий набір значень істинності простих висловлювань, при якому КНФ набуде значення F, що буде суперечити умові теореми.
Теорема доведена.
Таким чином, якщо нам необхідно встановити абсолютну істинність (хибність) складного висловлювання, то ми повинні:
1.Алгебраїчними перетвореннями звести складне висловлювання до КНФ (ДНФ).
2.Використовуючи критерій із теореми 6.10 (6.9), встановити абсолютну істинність (хибність) вихідного складного висловлювання або їх відсутність.
Залишається показати, що цю схему можна використовувати для довільного складного висловлювання.
114.Двоїстість висловлюв нь т їх вл стивості
Для того, щоб реалізувати згаданий вище підхід на практиці введемо необхідні означення. Означення. Нехай складне висловлювання A утворене з простих висловлювань A1, ... ,An та їх
заперечень лише за допомогою зв‘язок та . Висловлювання A’ будемо називати двоїстим висловлюванню A, якщо воно отримане з висловлювання A заміною зв`язок і на, відповідно, і та T і F, якщо вони зустрічаються у висловлюванні A на, відповідно, F і T.
Справедлива наступна
Теорема 6.12 (принцип двоїстості). Нехай A і B - складні висловлювання, A’ і B’ - відповідні їм двоїсті висловлювання. Тоді справедливі такі твердження:
а) якщо висловлювання A абсолютно істинне, то висловлювання  A’ абсолютно істинне;
A’ абсолютно істинне;
б) якщо висловлювання  A абсолютно істинне, то висловлювання A’ абсолютно істинне;
A абсолютно істинне, то висловлювання A’ абсолютно істинне;
в) якщо висловлювання A ~ B абсолютно істинне, то висловлювання A’ ~ B’ абсолютно істинне; г) якщо висловлювання A B абсолютно істинне, то висловлювання B’ A’ абсолютно
істинне.
Доведення твердження а).
Якщо висловлювання A абсолютно істинне, то його згідно теорем 6.10 та 6.11 можна подати у вигляді КНФ, яка містить в кожній елементарній диз‘юнкції контрарну пару або висловлювання T. Але тоді перехід від висловлювання А до двоїстого йому висловлювання А’ очевидно дозволить отримати висловлювання А’, що знаходиться в ДНФ, кожна елементарна кон` юнкція якої містить контрарну пару або висловлювання F. Виходячи з теореми 6.9, робимо висновок про те, що висловлювання А’
абсолютно хибне. Тоді  А’ є абсолютно істинним висловлюванням, що й потрібно було довести.
А’ є абсолютно істинним висловлюванням, що й потрібно було довести.
Доведення твердження б).
Якщо висловлювання 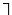 А абсолютно істинне, то висловлювання А можна подати у вигляді ДНФ, кожна елементарна кон`юнкція якої містить контрарну пару або висловлювання F. Тоді висловлювання А’, двоїсте висловлюванню А, буде мати вигляд КНФ, кожна диз‘юнкція якої містить контрарну пару або висловлювання T. Виходячи з теореми 6.10, робимо висновок, що висловлювання А’ абсолютно істинне, що й потрібно було довести.
А абсолютно істинне, то висловлювання А можна подати у вигляді ДНФ, кожна елементарна кон`юнкція якої містить контрарну пару або висловлювання F. Тоді висловлювання А’, двоїсте висловлюванню А, буде мати вигляд КНФ, кожна диз‘юнкція якої містить контрарну пару або висловлювання T. Виходячи з теореми 6.10, робимо висновок, що висловлювання А’ абсолютно істинне, що й потрібно було довести.
Доведення твердження в).
Як видно із таблиць істинності, висловлювання А В та А` В` набувають однакових значень істинності при однакових А і В, тому якщо А В абсолютно істинне, то А` В` також абсолютно істинне.
Доведення твердження г).
Як видно із таблиць істинності, висловлювання А В та В` А` набувають однакових значень істинності при однакових А та В, тому якщо А В абсолютно істинне, то В` А` також абсолютно істинне.
Теорема доведена.
Таким чином, від встановлення абсолютної істинності складних висловлювань можна переходити до встановлення абсолютної хибності двоїстих висловлювань. Інколи це буває зручно.
115.Озн чення числення висловлюв нь
1. Мов числення L.
1.1 Символи числення L:
а) пропозиційні літери: А, В, С, ... (інколи вони будуть з індексами);
б) символи зв`язок: , ; в) службові символи: ( , ) .
; в) службові символи: ( , ) .
1.2Довільна послідовність символів мови числення L називається виразом мови числення L.
1.3Формули мови числення L:
а) довільна пропозиційна літера є формулою;
134

б) якщо A, B - це формули мови L, то A B, |
A, B A, B - також формули мови L ; |
в) інших формул в численні L немає. |
|
2. Аксіоми числення L.
Якими б не були A, B, C наступні формули є аксіомами:
(А1) A (B A) ;
(А2) (A (B C)) ((A B) (A C)) ;
(А3) ( B (
B ( A)) ((
A)) (( B A) B) .
B A) B) .
3. Пр вил виведення числення L.
Числення L має єдине правило виведення Modus Ponens (MP): якщо мають місце формули A B і A, то має місце формула B.
Важливо уяснити, що правило виводення трактується, як деяке відношення на множині формул, яке двом засновкам у вигляді формул A B і A ставить у відповідність висновок у вигляді формули B.
Центральним поняттям формальних систем, як наголощувалоссь вище, є теорема або формула, що може бути виведена в численні. Настав час навести відповідні формальні означення.
Означення. Виводом в численні L будемо називати довільну послідовність формул, в якій кожна формула або є аксіомою, або отримана із попередніх формул послідовності за допомогою правила виведення. Остання формула виводу називається теоремою.
Наведене означення, очевидно, має конструктивний характер і спонукає до необхідності побудови зазначених послідовностей. Сам процес побудови виводу назвемо виведенням.
До н веденого вище озн чення числення висловлюв нь L необхідно зробити декільк в жливих
зув жень.
1.Ми визначили числення висловлювань L, але для цього використали іншу мову - українську мову.
Цю природну мову ми будемо називати метамовою, а саму мову числення висловлювань L мовоюоб`єктом. В метамові ми будемо використовувати прописні літери (курсив) латинського алфавіту для позначення формул мови-об`єкта.
Слід нагадати, що в пункті 1.1 означення мови числення висловлювань L знаки ‗:‘, ‗,‘ є метасимволами, а не символами мови числення L. За допомогою цих мета символів ми формуємо перелік певних символів мови числення висловлювань L. За метамову можемо використовувати інші природні мови.
2. Наведені аксіоми (А1), (А2), (А3) власне є формулами метамови, а не формулами мови числення висловлювань L. Їх варто сприймати як схеми аксіом, тобто генератори формул певного вигляду. Кожна з формул, яка має структуру відповідної схеми аксіом, і є аксіомою числення висловлювань L..
Кожну з схем аксіом ми будемо розглядати як сукупність формул, в яких на місце А, В, С можуть бути представлені будь-які з формул числення L. Вимагається тільки, щоб на місця всіх входжень формули А (В, С) була підставлена одна й та ж формула мови числення висловлювань L. Наприклад, аксіомами А1 є такі формули:
 А (А
А (А  А);
А);
(А1 А2) (А3 (А1 А2)); А3 ((А1 А2) А3) та інші.
3. В метамові той факт, що формула A є теоремою в числення висловлювань L. L будемо позначати | L A. Це означає, що існує послідовність формул мови L, яка задовольняє означенню виводу і в якій A є
останньою формулою. Читаеться так: « A виводиться в численні висловлювань L». Теореми інших числень будемо позначати, використовуючи той же знак, але конкретизуючи ім‘я числення. Якщо з контексту зрозуміло про яке числення висловлювань йде мова, наприклад до тих пір, доки ми не визначимо інших
числень, ім‘я числення висловлювань (у нашому випадку символ L) у знаку | L можна не писати.
4. У зв‘язку з тим, що в математиці часто використовується так зване виведення з гіпотезами, то в L можна говорити про виведення формули з якоїсь множини . Далі за допомогою | A будемо визначати, що A виводиться в L із множини формул , тобто існує послідовність формул числення висловлювань L, в якій кожна формула є аксіомою числення L, належить множині або отримана із попередніх формул послідовності за допомогою правила виведення. При цьому A є останньою формулою послідовності.
Очевидно, якщо є порожньою множиною, то | A має місце тільки тоді, коли А є теоремою, тобто тоді можемо записати | A.
Слід звернути увагу на те, що в численні висловлювань використовуються тільки символи зв‘язок імплікації та заперечення. Як і в алгебрі висловлювань це робиться для зменшення кількості операцій. Інші зв‘язки ми можемо виразити за допомогою імплікації та заперечення:
АВ означає  (А
(А  В);
В);
АВ означає  А В;
А В;
А~ В означає  ((А В)
((А В)  (В А)).
(В А)).
135


Нехай в i-тому рядку таблиці істинності формула A набуває значення T. Це можливо при таких
комбінаціях значень істинності формул B і C: |
|
|
|
|
1) |
формули B і C набувають значення F. |
|
|
|
За індуктивним припущенням виконується i |
| |
B. За метатеоремою 6.6 (пункт в) | |
B (B C). |
|
За правилом MP із двох останніх формул отримуємо i |
| B C, тобто i | A; |
|
||
2) |
формула B набуває значення F, формула C набуває значення T. |
|
||
Можна показати, що i | А, використовуючи ті ж міркування, що і для попереднього випадку; |
||||
3) |
формули B і C набувають значення T. |
|
|
|
За індуктивним припущенням виконується i |
| C. Продовжимо послідовність формулою С (B |
|||
C) (аксіома А1). За правилом MP з двох останніх формул отримуємо i | B C, тобто i | А.
Нехай в i-тому рядку формула A набуває значення F. Це можливо тільки тоді, коли формула B набуває
значення T, а формула C значення F. За індуктивним припущенням i | B і i |
| |
C. За метатеоремою 6.6 |
||
(пункт е) | B ( |
C (B C)). Двічі застосовуючи правило MP, отримуємо |
i |
| |
(B C), тобто i | |
 A.
A.
Метатеорема доведена.
На закінчення лекції варто навести приклади властивостей виводу, які встановили студенти. З одного боку, це продемонструє, що якими б складними не здавалися поняття й методи цього розділу математичної логіки, вони стають ефективними і зручними засобами розв‘язання практичних задач для більшості студентів. З іншого боку, це заохотить читачів до більш глибокого дослідження дедуктивних властивостей виводу.
Метатеорема 6.8 (студент А.Абдулах, група ІС-82). Якщо А | B і |
А | B, то | B. |
|
Доведення. Двічі застосувавши теорему дедукції дістанемо | А В і | |
А В. Формула (А В) |
|
(( А В) В) є теоремою числення L (метатеорема 6.6, пункт ж). Двічі застосовуючи правило виведення, отримуємо | В.
Метатеорема доведена.
Використовуючи метатеорему 6.8, легко встановити, наприклад, справедливість метатеореми 6.6
(пункт а): |
|
|
|
1) А (гіпотеза), А ( |
А А) (аксіома), |
А А (наслідок за правилом виведення), тобто |
А | |
А А; |
|
|
|
2) А (гіпотеза),
А (гіпотеза),  А (
А ( А А) (легко встановити, що це теорема в численні L),
А А) (легко встановити, що це теорема в численні L),  А А (наслідок за правилом виведення), тобто
А А (наслідок за правилом виведення), тобто  А |
А |  А А.
А А.
Отже, за метатеоремою 6.8 |  А А.
А А.
Студентом Є.Подласовим (група ФІ-71) метатеорема узагальнена.
Метатеорема 6.9 Нехай Г – множина формул. Якщо Г, А | B і Г, А | B, то | B.
А | B, то | B.
Доведення. Залишаємо його на самостійну роботу.
Слід зазаначити також, що побудову виводу в численні L треба розглядати як аналог гри за певними правилами. Ці правила прості і формальні. Тому компьютер можна легко навчити цій грі.
Поширені помилки студентів при виведенні теорем саме пов‘язані з бажанням перенести на виведення відомі тотожності булевої алгебри висловлювань, що порушує прийняті правила гри. Наприклад,
одержати теорему  А А із теореми А А заміною формули А на тотожну їй формулу
А А із теореми А А заміною формули А на тотожну їй формулу  А ми не маємо права. В той же час з виведеної теореми А А заміною ми можемо отримувати теореми
А ми не маємо права. В той же час з виведеної теореми А А заміною ми можемо отримувати теореми  А
А 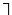 А,
А, 
 А
А  А та інші. Але тут мова йде не про тотожність, бо формула А не тотожна формулі
А та інші. Але тут мова йде не про тотожність, бо формула А не тотожна формулі  А, а про формальний прийом одержання нових формул тієї ж структури шляхом заміни.
А, а про формальний прийом одержання нових формул тієї ж структури шляхом заміни.
Варте уваги те, що згадане бажання здійсненне. Для цього треба визначити нове числення, в якому можна використовувати відповідні правила. Потрібно лише, щоб нові правила виведення зберігали абсолютну істинність засновків в висновках.
Тепер нам лишається довести, що числення L дійсно дозволяє відібрати істини певної сфери діяльності.
119.Повнот числення висловлюв нь L
Основна проблема, для розв‘язання якої створене числення висловлювань L, полягає у відборі істин певної сфери діяльності. Нехай множина висловлювань відносно цієї сфери діяльності буде позначена , а- підмножина істин, яка нас і цікавить.
Числення L характеризується множиною формул
та множиною теорем, визначеними, відповідно, генератором формул та механізмом виведення числення L.
Між та існує взаємооднозначна відповідність.
140 









 до раніше отриманих формул. Справедливість цього тверждення випливає з індуктивного означення формули.
до раніше отриманих формул. Справедливість цього тверждення випливає з індуктивного означення формули. , причому знову отримані формули, в свою чергу, включаються до процесу утворення нових і нових формул. Тому після того, як побудовані формули, що є пропозиційними літерами, в процесі побудови формул числення
, причому знову отримані формули, в свою чергу, включаються до процесу утворення нових і нових формул. Тому після того, як побудовані формули, що є пропозиційними літерами, в процесі побудови формул числення  і кожна формула може бути утворена тільки таким чином.
і кожна формула може бути утворена тільки таким чином.







