Теоретичні відомості.

Нехай для обчислення невідомих необхідно розв’язати системунелінійних рівнянь:

(1)

Для розв’язання систем нелінійних рівнянь зазвичай використовують ітераційні методи.

Метод простої ітерації

Систему рівнянь (1) представляємо у вигляді

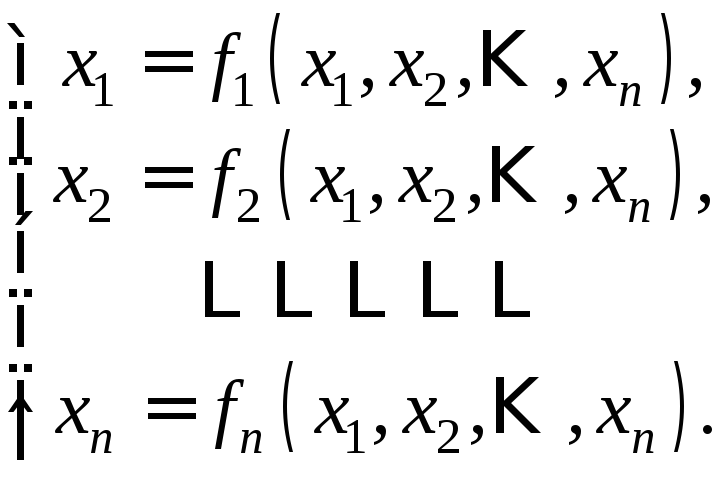(2)

Нехай в результаті початкового наближення були отримані такі наближення невідомих: . Тоді вирази для обчислення невідомих на наступній ітерації матимуть вигляд:

Ітераційний процес продовжується до тих пір, поки зміни всіх невідомих у двох послідовних ітераціях не стануть достатньо малими, т. б. абсолютні значення їхніх різниць не стануть меншими за дане мале число :

При використанні методу простої ітерації успіх визначається вдалим вибором початкових наближень невідомих: вони повинні бути достатньо близькими до реального розв’язку. У протилежному випадку процес може не зійтися.

Ітераційний процес збігається, якщо виконується співвідношення:

Для випадку двох невідомих та:

та

Метод Ньютона

Цей метод володіє значно більш швидкою збіжністю, ніж метод простої ітерації. В основі методу Ньютона для системи нелінійних рівнянь лежить розкладання функцій у ряд Тейлора, з якого викидаються члени, що містять похідні другого та вищих порядків.

Нехай в результаті початкового наближення були отримані такі наближення невідомих системи (1): відповідно. Покладаючи

, , …,,

отримуємо

(3)

Задача зводиться до знаходження приростів до значень невідомих.

Проведемо розкладання лівих частин (3) у ряд Тейлора, обмежуючись лише лінійними членами відносно приростів:

Оскільки згідно до (1) ліві частини цих виразів мають дорівнювати нулю, то прирівнюємо до нуля й праві частини. Отримуємо наступну систему лінійних відносно приростів алгебраїчних рівнянь:

(4)

Значення та їхні похідні обчислюються за умови

З коефіцієнтів системи (4) складаємо матрицю Якобі та знаходимо її визначник - якобіан:

Для існування єдиного розв’язку системи (4) необхідне виконання умови на кожній ітерації.

Таким чином, ітераційний процес розв’язання системи рівнянь (1) методом Ньютона полягає у визначенні приростів до значень невідомих на кожній ітерації. Ітераційний процес зупиняється, якщо всі прирости стають малими за абсолютною величиною:

У методі Ньютона також важливий вдалий вибір початкових наближень невідомих для забезпечення гарної збіжності.

Зразок виконання завдання

Завдання: 1) Розв’язати систему нелінійних рівнянь методом Ньютона з точністю до 0.001:

Розв’язання:

Відокремлення коренів проводимо графічно (рис. 2):

Рис. 2. Відокремлення коренів

З графіку бачимо, що система має єдиний розв’язок, що задовольняє умові. Він лежить в області D:

За початкове наближення приймаємо Маємо:

Якобіан системи за умови ,відмінний від нуля, т. б.

де

Обчислення проводимо за формулами Ньютона:

Отже, наступні наближення невідомих можна записати у вигляді

Значення та їхні похідні обчислюються за умови,.

Результати обчислень заносимо до таблиці:

n
0	0.4	0.75
1	0.50	-0.733
2	0.4940	-0.7083
3	0.4913	-0.7339
4	0.4912	-0.7335

Оскільки:

то ітераційний процес зупиняється. Отже,

Відповідь:

2) Розв’язати систему нелінійних рівнянь методом простої ітерації з точністю до 0.001:

Розв’язання:

Перепишемо дану систему у вигляді :

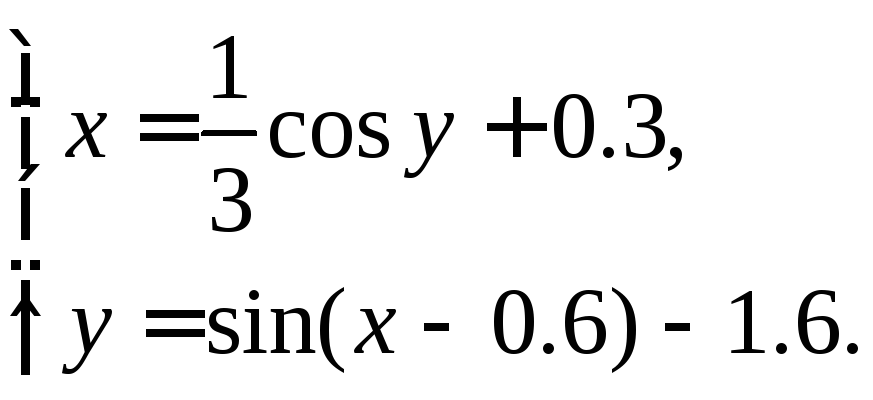
Відокремлення коренів проводимо графічно (рис. 3):

Рис. 3. Відокремлення коренів

З графіку бачимо, що система має єдиний розв’язок, що лежить в області D:

Упевнимося, що метод простої ітерації є збіжним для уточнення розв’язку даної системи. Для цього запишемо її у наступному вигляді:

Оскільки

то в області D маємо:

Таким чином умови збіжності виконуються.

Обчислення проводимо за формулами:

За початкове наближення приймаємо , .

Результати обчислень заносимо до таблиці:

n
0	0.15	-2.1
1	0.1317	-2.0513
2	0.1459	-2.0386
3	0.1497	-2.0353
4	0.1507	-2.0343
5	0.1510	-2.0341

Оскільки:

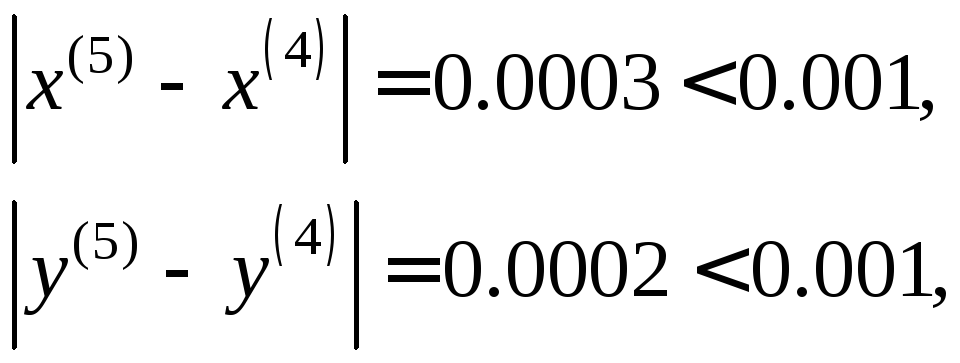
то ітераційний процес зупиняється. Отже,

Відповідь: